UNIVERSIT DEGLI STUDI DI NAPOLI FEDERICO II Scuola

UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II Scuola Politecnica e delle Scienze di Base Dipartimento di Ingegneria Industriale Monitoraggio e Diagnostica Prof. Vincenzo Niola

Introduzione Si affronterà lo studio di segnali allo scopo di effettuare il monitoraggio e la diagnostica di sistemi meccanici. Si prenda, ad esempio, in considerazione lo studio di una qualsiasi coppia cinematica: si osservino le vibrazioni cui è soggetta la coppia; esse si possono vedere come un rumore sovrapposto al normale funzionamento della coppia stessa. Se si misurano opportunamente tali vibrazioni mediante un accelerometro è possibile effettuare un’analisi sullo stato di usura della coppia stessa.

Introduzione Da questo semplice esempio si evince l’importanza che assume la misura del rumore in tale analisi. E’ da essa infatti che si evincono interessanti considerazioni. Pertanto, al fine di determinare lo stato di usura o di rilevare un principio di mal funzionamento, è necessario un livello di dettaglio molto spinto: le misure su cui si porrà l’attenzione, infatti, non verranno mai filtrate per non ridurre il contenuto informativo del segnale.

Introduzione L’analisi dettagliata ci permetterà di distinguere il rumore vero e proprio dalle anomalie di funzionamento del sistema meccanico. Ad esempio, se si lavora su un segnale che rappresenta l’accelerazione di una massa, la presenza di uno spike indicherà un movimento brusco della stessa e ciò potrebbe essere considerato come principio di un problema (ad esempio il generarsi di una cricca). È possibile in generale fare ciò perché qualsiasi sistema meccanico, prima di portarsi alla rottura, presenta comportamenti anomali che possono essere rilevati, cioè delle avvisaglie vere e proprie.

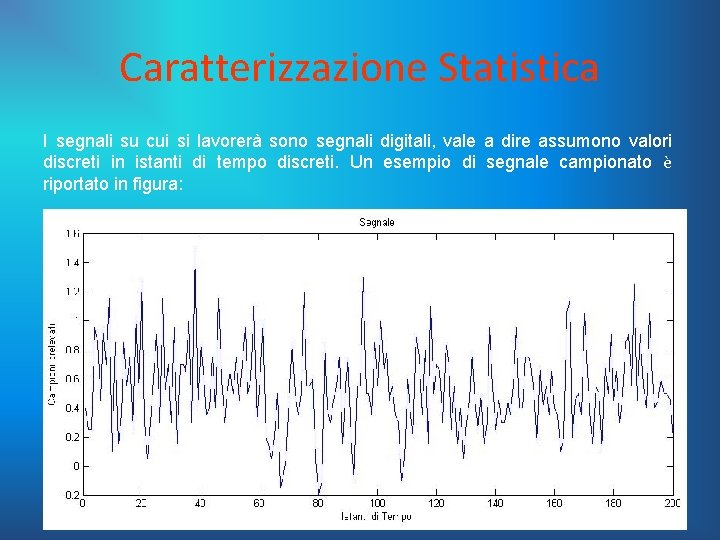
Caratterizzazione Statistica I segnali su cui si lavorerà sono segnali digitali, vale a dire assumono valori discreti in istanti di tempo discreti. Un esempio di segnale campionato è riportato in figura:

Caratterizzazione Statistica Essendo il segnale di natura digitale, è possibile diagrammare le frequenze relative di ogni valore che il segnale assume:

Caratterizzazione Statistica Si dice frequenza relativa dell’evento X, e si indica con , il valore: ove con N si indica il numero totale degli esperimenti fatti e con Nx il numero di volte in cui l’esperimento ha restituito come valore proprio X. Nel caso in esame è da intendersi come esperimento il campionamento e come numero totale di esperimenti il numero di campioni cui si compone il segnale. Si osservi, però, che sull’asse delle ordinate è stato riportato il nome della funzione di probabilità Pr(x), coerentemente con la definizione di probabilità di Von Mises (o frequentista) secondo la quale si può scrivere: Quindi, per N grande, la probabilità è definita come la frequenza relativa dell’evento. Una maniera più efficace e sintetica per la caratterizzazione del segnale in analisi è l’uso di indicatori statistici.

Indicatori Statistici Un indicatore statistico è una funzione di un insieme finito o infinito di valori. Esistono molti tipi di indicatori statistici, adoperati nei diversi settori, ma essenzialmente sono raggruppabili in tre categorie: 1. Indicatori di Posizione: che in qualche modo stabiliscono l’ordine di grandezza del segnale 2. Indicatori di Dispersione: che esprimono il grado di disordine del segnale 3. Indicatori di Simmetria: analizzati nel seguito.

Indicatori Statistici Media: Viene calcolata sommando i diversi valori a disposizione, i quali vengono divisi con il numero complessivo di valori. La formula della media aritmetica semplice è: ovvero, se si utilizza il simbolo della sommatoria: La media, come tutti gli indici di posizione, indica all'incirca l'ordine di grandezza (la posizione sulla scala dei numeri, appunto) dei valori esistenti.

Indicatori Statistici In particolare si dice che: qualora si hanno N valori, con media Ma, allora per conoscere la somma di tutti questi valori è sufficiente moltiplicare N con Ma. Questo, permette di avere un'idea della quantità complessiva qualora si conosca soltanto il valore medio e quanti valori sono presenti. Che si tratti di un indicatore di posizione lo si verifica facilmente, in quanto se si aggiunge a tutti i valori una stessa quantità allora la media è anch'essa aumentata di quella stessa quantità. Inoltre, se si moltiplicano tutti i valori con un determinato numero, allora anche la media aritmetica viene moltiplicata con tale numero.

Indicatori Statistici Momento: In statistica, il momento semplice di ordine k di una variabile casuale è definito come la media della k-esima potenza dei valori dove pi denota la funzione di massa di probabilità della variabile casuale. Il momento centrale di ordine k è definito come la media della k-esima potenza dello scarto dalla media μ = μ 1 dove μ denota il valore atteso della variabile casuale.

Indicatori Statistici Mediana: La mediana è il valore (o l'insieme di valori) di una distribuzione X per cui la frequenza cumulata vale 0, 5. Pertanto bipartisce la distribuzione. Usualmente si indica la Mediana con Me. Se le modalità sono raggruppate in classi non si definisce un valore univoco, ma una classe mediana Xi − Xi+1. La determinazione di tale classe avviene considerando le frequenze cumulate; indicando con Fi la generica frequenza cumulata dell'osservazione i-esima sarà: Fi + 1 > 0, 5 e Fi < 0, 5. Pur essendo corretto considerare un qualsiasi elemento dell'intervallo Xi − Xi+1 un valore mediano, si è soliti procedere, al fine di avere una misura unica del valore, a un'approssimazione della mediana con la seguente formula:

Indicatori Statistici La mediana è un indice di posizione. Una proprietà della mediana è di rendere minima la somma dei valori assoluti degli scarti delle xi da un generico valore

Indicatori Statistici Moda: La moda della distribuzione di frequenza X è - in statistica - la modalità (o la classe di modalità) caratterizzata dalla massima frequenza e viene spesso rappresentata con la simbologia ν 0. In altre parole, è il valore che compare più frequentemente. Una distribuzione è unimodale se ammette un solo valore modale, è bimodale se ne ammette due, trimodale se ne ha tre, ecc. Per la determinazione della classe modale è opportuno ricorrere al criterio dell‘istogramma individuando il rettangolo di altezza massima. La classe con la maggiore densità media (che corrisponde all'altezza dell'istogramma) è quella modale. Indicando con N(x(i), (x(i+1)) il numero di elementi che cadono nella classe x(i), x(i+1), l'altezza h(i, i+1) sarà data da: h(i, i+1)=N(x(i), x(i+1))/(x(i+1)-x(i))

Indicatori Statistici Varianza: In statistica la varianza è un indice di dispersione. Viene solitamente indicata con σ2 (dove σ è la deviazione standard). L'espressione per la varianza, nell'ambito della statistica descrittiva, è dove μ rappresenta la media aritmetica dei valori xi. Nel caso si tratti di valori ponderati, allora la definizione diventa: (in questo caso μ è la media aritmetica ponderata).

Indicatori Statistici Covarianza: In statistica la covarianza è un indice che misura la "contemporaneità" della variazione (in termini lineari) di due variabili; si utilizza spesso la notazione: dove essendo µx e µy rispettivamente la media aritmetica delle serie di valori x e delle serie di valori y.

Indicatori Statistici La covarianza può assumere sia valori positivi che negativi. Nella statistica inferenziale, quando due variabili sono tra di loro indipendenti, allora la loro covarianza è nulla (l'inverso non è necessariamente verificato). A volte la covarianza viene citata mnemonicamente come la media del prodotto degli scarti dalla media. La covarianza può essere scomposta in due termini, diventando ovvero la media dei prodotti meno il prodotto delle medie.

Indicatori Statistici Quando y=x, allora la covarianza si trasforma in varianza: Dividendo la covarianza per la deviazione standard di ciascuna delle due serie di variabili, si ottiene l'indice di correlazione di Pearson:

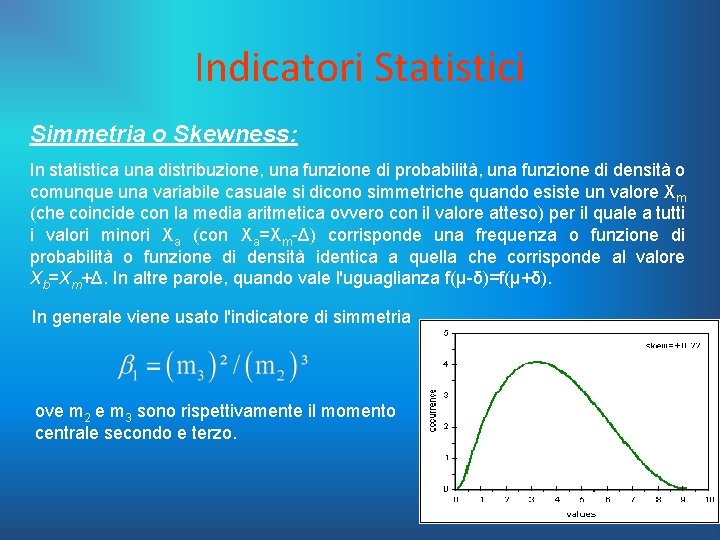
Indicatori Statistici Simmetria o Skewness: In statistica una distribuzione, una funzione di probabilità, una funzione di densità o comunque una variabile casuale si dicono simmetriche quando esiste un valore Xm (che coincide con la media aritmetica ovvero con il valore atteso) per il quale a tutti i valori minori Xa (con Xa=Xm-Δ) corrisponde una frequenza o funzione di probabilità o funzione di densità identica a quella che corrisponde al valore Xb=Xm+Δ. In altre parole, quando vale l'uguaglianza f(μ-δ)=f(μ+δ). In generale viene usato l'indicatore di simmetria ove m 2 e m 3 sono rispettivamente il momento centrale secondo e terzo.

Indicatori Statistici Tale indicatore è • =0, nel caso di perfetta simmetria • <0, per l'asimmetria a destra • >0, per l'asimmetria a sinistra Talvolta in luogo di β 1 si usa la sua radice: Entrambi hanno lo svantaggio che possono assumere valore nullo anche in presenza di asimmetria. Un altro importante indice di asimmetria è l'indice di asimmetria di Pearson. : ove ν 0 è la moda, che ha come difetto il fatto che è applicabile solo a distribuzioni unimodali, non è normalizzato ed Sk=0 è una condizione necessaria ma non sufficiente per una simmetria.

La Trasformata Wavelet La parola wavelet, ondina, ha origine nei primi anni ottanta ed è dovuta a Morlet e Grossman che infatti usavano la parola francese ondelette - "piccola onda". Poco più tardi la parola venne convertita in inglese traducendo "onda" ("onde" in francese) in "wave" - ottenendo wavelet. Le trasformate wavelet sono classificate a livello generale nella trasformata wavelet discreta (Discrete Wavelet Transform, DWT) e nella trasformata wavelet continua (Continuous Wavelet Transform, CWT). La differenza di principio fra le due è il fatto che la trasformata continua opera su tutte le possibili scale e traslazioni, mentre la trasformata discreta usa un sottoinsieme finito di tutti i valori possibili. Lo sviluppo delle wavelet può essere collegato a diverse correnti di pensiero separate, che hanno origine dal lavoro di Haar all'inizio del ventesimo secolo.

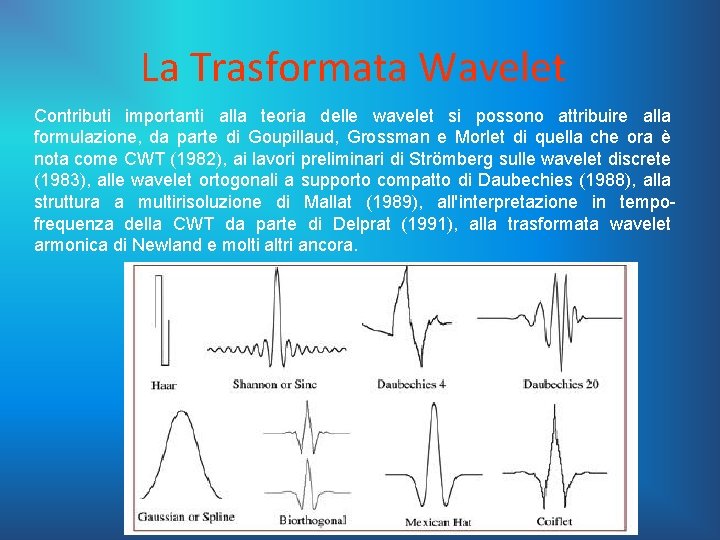
La Trasformata Wavelet Contributi importanti alla teoria delle wavelet si possono attribuire alla formulazione, da parte di Goupillaud, Grossman e Morlet di quella che ora è nota come CWT (1982), ai lavori preliminari di Strömberg sulle wavelet discrete (1983), alle wavelet ortogonali a supporto compatto di Daubechies (1988), alla struttura a multirisoluzione di Mallat (1989), all'interpretazione in tempofrequenza della CWT da parte di Delprat (1991), alla trasformata wavelet armonica di Newland e molti altri ancora.

Settori di Applicazione Generalmente, la DWT è usata nella codifica dei segnali mentre la CWT è usata nell'analisi dei segnali. Di conseguenza, la DWT è usata comunemente in ingegneria e informatica e la CWT è usata più spesso nella ricerca scientifica. Le trasformate wavelet sono ora adottate in un gran numero di applicazioni, spesso sostituendo la trasformata di Fourier convenzionale. Molte aree della fisica hanno visto questo cambiamento di paradigma, incluse dinamica molecolare, calcolo ab initio, astrofisica, geofisica sismica, ottica, turbolenza e meccanica quantistica. Altre aree che stanno vedendo questo cambiamento sono elaborazione delle immagini, pressione del sangue, battito del cuore e analisi dell'ECG, analisi del DNA, analisi delle proteine, climatologia, elaborazione dei segnali in generale, riconoscimento vocale, computer graphics, e analisi multifrattale.

Scomposizione dei segnali Nel corso della storia i matematici hanno proposto vari metodi di scomposizione dei segnali, metodi che hanno in comune la stessa interpretazione geometrica, ossia ogni segnale rappresentato da una funzione viene proiettato su una base ortogonale, pertanto risulta scomposto nelle sue componenti lungo gli elementi della base stessa. Tali componenti vengono chiamate coefficienti del segnale. I diversi metodi si distinguono proprio nella base adoperata per la scomposizione. L’analisi di Fourier usa come base un insieme di infinite funzioni e Il significato delle componenti del segnale scomposto in questa base è ben noto come contenuto armonico del segnale. La trasformata Wavelet adopera una base composta da infinite funzioni a durata limitata, tali funzioni prendono il nome di Wavelet. Si approfondirà il caso delle Wavelet di Haar. Il significato delle componenti del segnale scomposto è meno ovvio rispetto al caso di Fourier. .

Trasformata di Fourier Prima di introdurre la base adoperata nella trasformata Wavelet, è opportuno vedere più in dettaglio la scomposizione secondo Fourier. Si affronterà in seguito il problema del confronto tra i due tipi di metodi. Come già detto, la scomposizione secondo Fourier adopera una base composta da funzioni del tipo: Per semplicità si consideri come spazio in cui prendere i segnali da scomporre, lo spazio osservando che una funzione definita su un intervallo generico può sempre essere opportunamente scalata e ricondotta all’intervallo Si osservi preliminarmente che le funzioni introdotte sono tutte a valor medio pari a zero eccetto che per ( ed è escluso dalla serie). E’ quindi conveniente isolare dalla serie il coefficiente che moltiplica che assume il significato di componente continua del segnale da scomporre: .

Trasformata di Fourier È possibile dimostrare ora che costituiscono una base ortogonale.

Trasformata di Fourier Per soddisfare anche il requisito di normalità si devono considerare, piuttosto che le funzioni poco prima mostrate, le seguenti: Queste esprimono quindi la base CONS (Complete orthonormal system) utilizzata da Fourier.

Trasformata di Fourier I coefficienti , presenti nelle relazioni della precedente slide sono esprimibili come componenti del segnale lungo le funzioni : che esplicitati diventano: Lo studio di Fourier si conclude quindi con il calcolo di queste.

Trasformata di Fourier Analizzando i coefficienti dello sviluppo si determinano importanti proprietà del segnale in analisi, come il suo valor medio ( ), la parità ( ) o la disparità ( ). Inoltre, combinando i coefficienti nei coefficienti: si riescono ad introdurre gli andamenti di spettro di ampiezza e spettro di fase molto utili nelle applicazioni scientifiche. Resta da risolvere il problema legato al troncamento della serie. A seconda dell’applicazione si riesce sempre a trovare una frequenza massima di interesse, al di sopra della quale non è più necessario studiare il contenuto armonico.

Limiti della Trasformata di Fourier La trasformata di Fourier è un tool perfetto per trovare le componenti frequenziali di un segnale, fornendo la possibilità di affrontare problemi nel dominio della frequenza, con una notevole semplificazione dello studio. Tuttavia tale strumento non si presta per la descrizione completa del segnale, vale a dire che segnali diversi potrebbero presentare spettri simili.

La Trasformata Wavelet La Trasformata di Fourier

Analogie: trasformata di Fourier e Wavelet Fourier Funzioni base Coefficienti Wavelet

La trasformata di Fourier Si può ricostruire un segnale con buona approssimazione utilizzando un numero finito di armoniche

La trasformata di Fourier

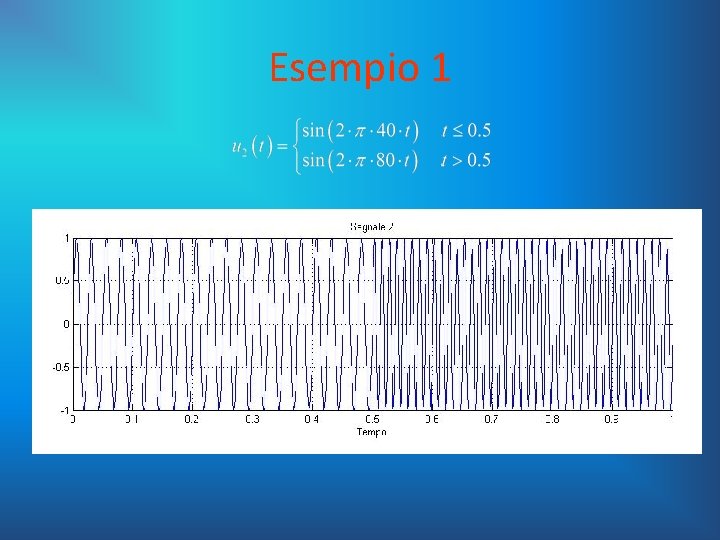
Esempio 1 A titolo di esempio si analizzano i seguenti due segnali restringendo l’attenzione all’intervallo :

Esempio 1

Esempio 1 Si osservi nella seguente figura come i due spettri di frequenza presentino pressoché lo stesso andamento:

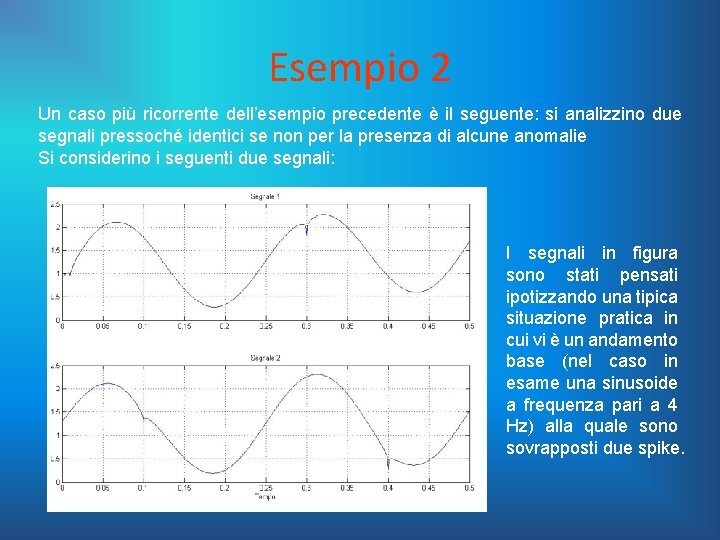
Esempio 2 Un caso più ricorrente dell’esempio precedente è il seguente: si analizzino due segnali pressoché identici se non per la presenza di alcune anomalie Si considerino i seguenti due segnali: I segnali in figura sono stati pensati ipotizzando una tipica situazione pratica in cui vi è un andamento base (nel caso in esame una sinusoide a frequenza pari a 4 Hz) alla quale sono sovrapposti due spike.

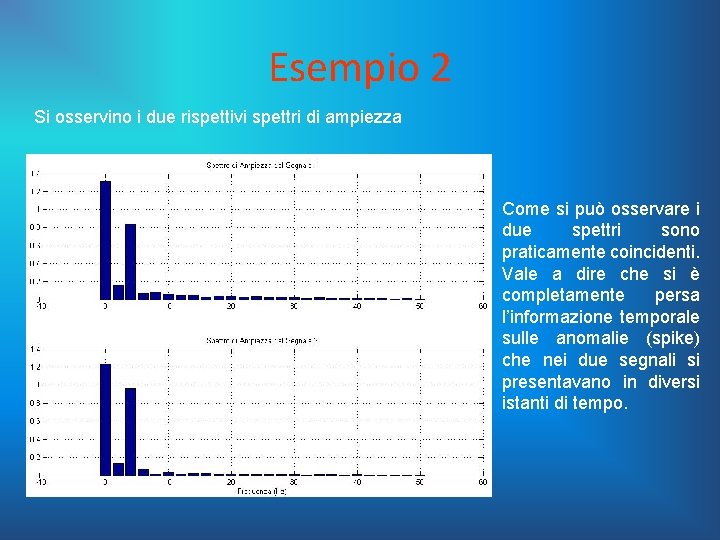
Esempio 2 Si osservino i due rispettivi spettri di ampiezza Come si può osservare i due spettri sono praticamente coincidenti. Vale a dire che si è completamente persa l’informazione temporale sulle anomalie (spike) che nei due segnali si presentavano in diversi istanti di tempo.

Trasformata Wavelet continua (CWT) Nella sua accezione più generale si definisce trasformata Wavelet continua: Tale formulazione mostra come la funzione viene decomposta mediante l’insieme di funzioni chiamate wavelet. Le variabili sono i parametri di scala e traslazione rispettivamente, e l’asterisco denota l’operazione di complesso coniugato. Per completezza si riporta anche la trasformata Wavelet inversa:

Trasformata Wavelet continua (CWT) L’insieme delle wavelet è generato a partire da una wavelet di base wavelet madre, attraverso scalature e traslazione della stessa: detta Il termine è necessario ai fini della normalizzazione dell’energia quando si effettua la scalatura. È importante notare come nella definizione non risultano esplicitate le funzioni wavelet di base. La teoria delle trasformate wavelet prescinde pertanto dalla natura delle funzioni utilizzate come wavelet base. Questo concede un grado di libertà all’utente della trasformata consentendogli la possibilità di scegliere le wavelet che più si adattano alle sue esigenze, nel rispetto di alcune proprietà di seguito riportate.

Proprietà della Wavelet Le più importanti proprietà delle wavelet sono le condizioni di ammissibilità e regolarità. Condizione di ammissibilità: Si può dimostrare che le funzioni condizione di ammissibilità: a quadrato integrabile, che soddisfano la possono essere adoperate per l’analisi e la successiva sintesi del segnale senza la perdita di informazioni. Nella condizione di ammissibilità indica la trasformata di Fourier di.

Proprietà della Wavelet Nella condizione di ammissibilità è intrinseco il fatto che infinitesimo di ordine maggiore o uguale a , pertanto: è per un Tale ultima condizione e quella di ammissibilità implicano che le Wavelet hanno uno spettro del tipo passa-banda. L’annullarsi di essere nullo: e quindi a frequenza nulla significa anche il valor medio di deve essere di tipo oscillante. In altri termini deve essere un’onda.

Proprietà della Wavelet Condizione di regolarità: Un’altra importante proprietà è quella della regolarità che si esprime mediante l’annullamento del momento: ove n è il numero di momenti nulli. Se una wavelet ha n momenti nulli allora l’ordine di approssimazione della trasformata wavelet è anch’esso di ordine n. Dal punto di vista pratico, un’onda con un elevato numero di momenti nulli tende velocemente a zero e si può quindi affermare che ha una durata limitata. Non è necessario in realtà che il momento sia esattamente nullo, ma sono sufficienti valori prossimi allo zero. Infatti ricerche sperimentali suggeriscono che il numero di momenti nulli richiesti dipendono fortemente dall’applicazione.

Supporto Data una funzione si definisce supporto l’insieme degli elementi del dominio in cui è diverso da zero: Per le wavelet il supporto è in generale un intervallo compatto. La definizione di supporto è importante perché individua la regione temporale in cui opera la wavelet considerata.

Osservazione La definizione di trasformata Wavelet continua non è direttamente applicabile perché presenta alcune complicazioni: 1. Ridondanza: le wavelet scalate e traslate così come sono state definite, non costituiscono una base ortogonale. 2. Numero infinito di wavelet: per la validità della definizione bisogna utilizzare un’infinità di onde wavelet Tali problematiche saranno affrontate e risolte nel seguito.

Wavelet discrete Per risolvere il problema della ridondanza si introducono le wavelet discrete. Il termine discreto non sta ad indicare che si tratteranno segnali discreti, piuttosto vuole metter in luce che l’insieme è ottenuto facendo variare in maniera discreta. Dunque per definire una wavelet discreta si usa la seguente: in luogo di: ove al posto degli indici compaiono , rappresenta il passo di dilatazione e è il fattore di traslazione, j è l’indice di scala, k l’indice di traslazione. In questo modo agendo sugli indici j, k è comunque possibile scalare e traslare l’onda, ma data la loro natura l’insieme è un’infinità numerabile.

Wavelet discrete Quando si effettua una trasformata Wavelet di un segnale continuo utilizzando delle wavelet discrete il risultato sarà una serie di coefficienti. Ci si riferisce a questa situazione dicendo che si è operata una Wavelet Series Decomposition. Si noti che per risolvere il problema della ridondanza senza perdere la possibilità di ricostruire il segnale, le devono formare un sistema CONS. Per costruire il sistema CONS desiderato deve accadere che la wavelet madre deve rispettare la seguente condizione al variare di j, k:

Wavelet discrete Un segnale arbitrario può pertanto essere ricostruito utilizzando le funzioni wavelet di base ortogonali, pesate con i coefficienti delle trasformate wavelet: con

Interpretazione spettrale Utilizzando: è possibile ricostruire il segnale mediante i coefficienti calcolati con la: Al fine di capire meglio come opera la trasformata wavelet e dare un’interpretazione più profonda dei coefficienti si affronta lo studio di Fourier delle wavelet definite come:

Interpretazione spettrale Come già detto l’insieme è ottenuto mediante successive operazioni di scalamento e traslazione su di una wavelet madre. Si osservi che (se , com’è in generale) un indice è responsabile di una compressione della wavelet madre, viceversa genera una dilatazione, ritarda il supporto, lo anticipa. Com’è noto dalla teoria di Fourier, un’operazione di traslazione non altera lo spettro (delle ampiezze) di un segnale in termini di banda; mentre l’operazione di scalamento produce il seguente effetto: ossia ad una compressione nel tempo corrisponde una dilatazione in frequenza dello stesso fattore (e viceversa).

Interpretazione spettrale È noto inoltre che ogni wavelet ha uno spettro del tipo passa-banda. Al variare dell’indice di scala j allora la corrispondente wavelet andrà ad occupare una zona ben precisa dell’asse spettrale, viceversa una variazione dell’indice k non altera lo spettro, ma serve a localizzare nel tempo la wavelet. Quindi, mediante j si individua un intervallo di frequenze, mentre mediante k si individua un intervallo di tempo. È per questo motivo che conoscere un coefficiente significa avere una informazione simultanea di tempo e frequenza. Affinché quanto detto valga in maniera esatta è necessario che al variare di j e k vengano coperti tutto l’asse frequenziale e tutto l’asse temporale. Scegliendo e si raggiunge l’obiettivo. (La scelta non è arbitraria, ma consente di avere una diltatazione/compressione diadica, quindi una suddivisione diadica dell’asse delle frequenze, ed una traslazione intera).

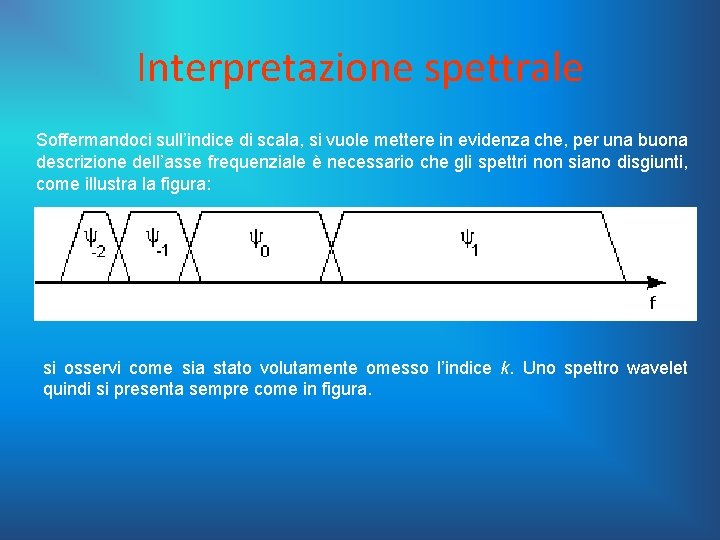
Interpretazione spettrale Soffermandoci sull’indice di scala, si vuole mettere in evidenza che, per una buona descrizione dell’asse frequenziale è necessario che gli spettri non siano disgiunti, come illustra la figura: si osservi come sia stato volutamente omesso l’indice k. Uno spettro wavelet quindi si presenta sempre come in figura.

La funzione di scala Risolto il problema della ridondanza, si prenda in considerazione il problema della riduzione del numero di termini della sommatoria: da infinito a finito. Si pone, pertanto, il problema dell’approssimazione mantenendo una buona qualità della trasformata. Le traslazioni delle wavelet sono naturalmente limitate dalla durata del segnale in esame, cosicché si ottengono i limiti entro cui far variare l’indice k. Questo però lascia l’interrogativo sulla dilatazione: di quante scale si ha bisogno per analizzare il segnale in considerazione? Come si possono ottenere i limiti entro cui far variare j?

La funzione di scala È immediato verificare che è possibile assegnare un limite superiore per le j considerando la banda del segnale (se il segnale è a banda finita) oppure fissando una frequenza limite oltre la quale non si è più interessati all’analisi. Rimane da determinare il limite inferiore. Osservando attentamente il modo con cui gli spettri delle wavelet più dilatate si addensano verso la frequenza zero si intuisce che per avere una buona copertura delle basse frequenze è necessario utilizzare molte wavelet sempre più dilatate, inoltre, il valore a frequenza nulla non è mai coperto (ciò è dovuto al fatto che tutte le wavelet presentano valor medio nullo). La teoria suggerisce quindi di utilizzare un numero infinito di wavelet con Il problema però può essere aggirato mediante l’uso di una funzione di tipo passa-basso , chiamata funzione di scaling, o funzione di scala. .

La funzione di scala Vale dire che fissando un limite inferiore per j, si può coprire la restante parte dello spettro utilizzando la funzione di scaling al posto delle infinite wavelet necessarie. La figura chiarisce quanto detto: Chiaramente, agire in questo modo, dal punto di vista della rappresentazione del segnale, significa perdere informazione, ma si ottiene il vantaggio non indifferente di adoperare una trasformata wavelet mediante un numero finito di onde.

La funzione di scala Da quanto detto risulta motivata la scelta del nome della funzione di scaling: essa fissa la dilatazione, quindi la scala massima; tutte le altre wavelet hanno durata inferiore e consentono l’analisi dettagliata del segnale all’interno della scala fissata, fino al raggiungimento del livello di dettaglio desiderato. Fissare la scala quindi significa porre un limite alle possibili dilatazioni delle wavelet. Ciò non toglie che anche le funzioni di scala devono essere traslate per coprire tutto l’asse temporale d’interesse, ma come già detto queste traslazioni sono naturalmente limitate dalla durata stessa del segnale. Il problema pertanto è risolto.

La funzione di scala Affinché la funzione di scaling abbia uno spettro di tipo passa-basso è necessario che il momento di ordine zero non sia nullo: ove si è scelto di porlo uguale a uno per la normalizzazione dell’energia. I momenti di ordine superiore invece devono essere nulli. Questo comporta che anche la funzione di scala ha una durata limitata e quindi anche per essa si definisce un supporto. Si osservi che da punto di vista analitico, la funzione di scala presenta il contenuto armonico di tutte le infinite wavelet sottese dal suo spettro. Pertanto la può anch’essa essere vista come una serie di wavelet discrete: ove la sommatoria interessa infiniti termini per .

La funzione di scala La funzione di scaling da utilizzare dipende dal limite inferiore di j. Aumentare tale limite a j+1 significa: • includere altri termini nella • allargare lo spettro della e spingere l’analisi verso le alte frequenze. Da quanto appena detto si intuisce anche lo scaling al livello j è ottenibile da quello al livello j+1 (in quanto contiene più informazioni), ovvero: ossia combinando più funzioni di scaling traslate mediante i coefficienti . La precedente è anche chiamata two-scale relation e mette in evidenza che scale con j crescenti contengono informazioni crescenti, sempre più dettagliate.

La funzione di scala Tutto quanto detto finora suggerisce di adoperare i due indici j, k anche per identificare una ben determinata funzione di scaling: starà quindi ad indicare una funzione che copre lo spettro di tutte le wavelet e. Quindi anche le scalamenti di una possono essere viste come ottenute da traslazioni e. Mediante queste ultime considerazioni e ricordando: • • si conclude che un segnale può essere rappresentato anche mediante una serie di funzioni di scala.

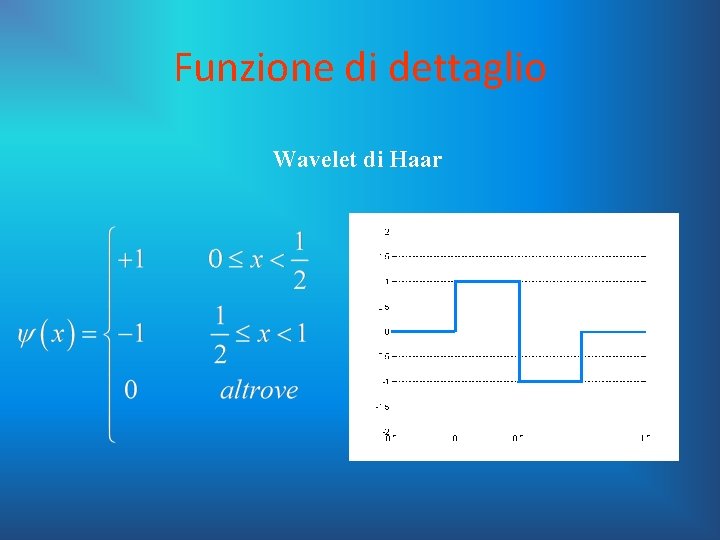
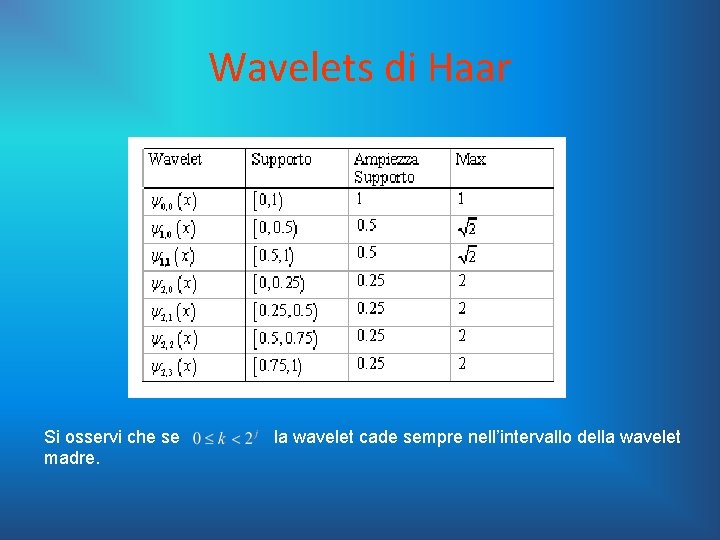
Il sistema base di Haar Si affronta adesso lo studio di una base wavelet, ottenuta adoperando come onda madre la funzione di Haar. La funzione di Haar Si definisce la funzione di Haar come segue: È immediato verificare che tale funzione gode di tutti i requisiti per poter generare una famiglia di wavelet e che:

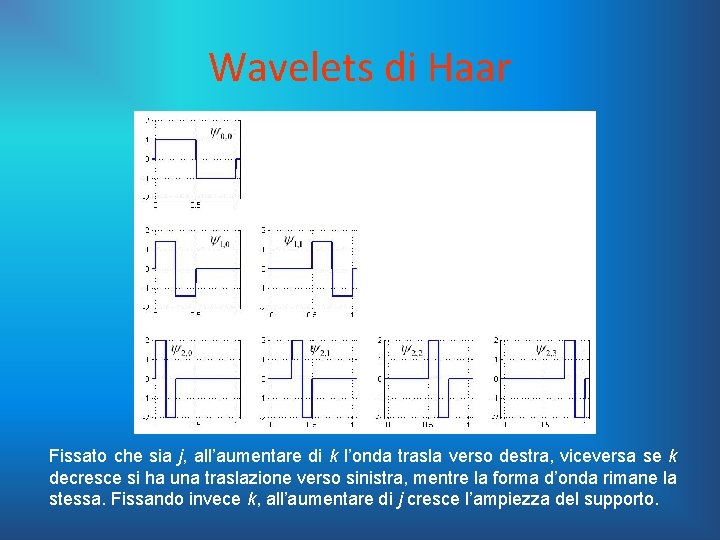
Wavelets di Haar Per ottenere l’intera famiglia di wavelet a partire dalla funzione madre basta introdurre gli indici j, k. Per verificare quanto detto precedentemente si riportano dei grafici in cui si fanno variare con una certa sistematicità i parametri j, k.

Wavelets di Haar Fissato che sia j, all’aumentare di k l’onda trasla verso destra, viceversa se k decresce si ha una traslazione verso sinistra, mentre la forma d’onda rimane la stessa. Fissando invece k, all’aumentare di j cresce l’ampiezza del supporto.

Funzione di dettaglio Wavelet di Haar

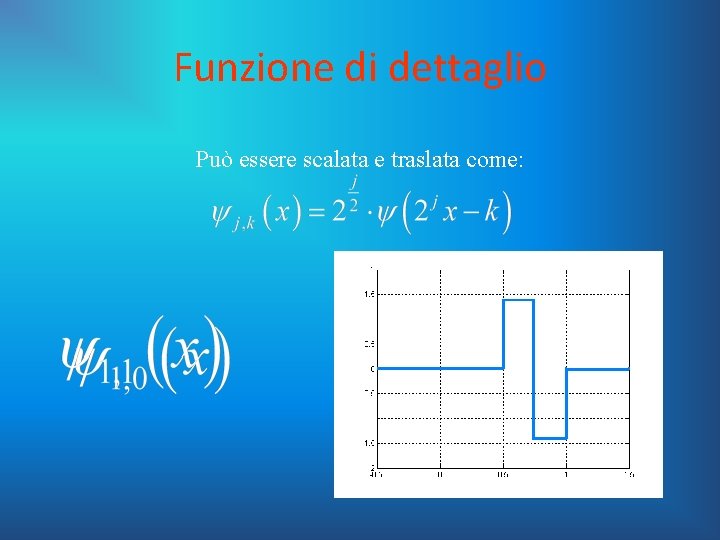
Funzione di dettaglio Può essere scalata e traslata come:

Funzione di dettaglio Può essere traslata e scalata come:

Wavelets di Haar Si osservi che se madre. la wavelet cade sempre nell’intervallo della wavelet

Wavelets di Haar La base di Haar è un sistema ortonormale completo Dimostriamo dapprima che l’insieme è ortonormale: Notiamo per prima cosa che per ogni funziona di Haar è soddisfatta la seguente: Notiamo poi che il supporto di una generica onda è: e che due wavelet avente stesso indice j, ma diverso k, non avranno mai due supporti che si sovrappongono, e perciò sono ortogonali. Se invece due wavelet hanno differenti indici di dilatazione j e j’, con j’<j, e stesso indice k, allora il risulta essere e le due funzioni risultano essere ancora ortogonali.

Wavelets di Haar In sintesi: Dal momento che: allora il sistema base di Haar risulta essere anche ortonormale.

Wavelets di Haar E’ possibile ora che il sistema è completo: Per dimostrare la completezza del sistema bisogna dimostrare che ogni funzione può essere approssimata arbitrariamente bene tramite una combinazione lineare delle. Per prima cosa notiamo che qualsiasi funzione definita in approssimata a mezzo di una funzione avente il supporto compatto: può essere Scegliendo quindi un intero grande a piacere, si può approssimare a piacere la funzione. Dunque la prima approssimazione che si effettua è una restrizione di , da a , che può essere denotata con.

Wavelets di Haar Una seconda approssimazione consiste nel passare dalla in una funzione continua a tratti su intervalli del tipo dove può essere scelto grande a piacere tanto da rendere buona l’approssimazione quanto si vuole.

Wavelets di Haar La seguente figura mostra quanto appena detto: il segnale originario in rosso può essere approssimato sempre meglio al crescere di

Wavelets di Haar Passiamo ad una dimostrazione intuitiva della proprietà di completezza. Si dica una funzione continua a tratti su intervalli di lunghezza il valore di tale funzione nell’ intervallo Osserviamo che la funzione e si : è esprimibile come somma di due funzioni: ove è l’approssimazione di di qualità immediatamente inferiore ad. E’ possibile immaginare come un’approssimazione di. Se si interpretano così le cose, allora la funzione di rappresenta i dettagli da aggiungere ad per ottenere , per questo ci si riferisce ad essa come funzione di dettaglio.

Wavelets di Haar Per capire meglio quanto appena detto si osservi la seguente figura: In essa sono riportate a tratto blu la funzione originale e le sue approssimazioni di livello due e tre (si può risalire al livello dell’approssimazione dalla dimensione degli intervalli di continuità).

Wavelets di Haar E’ allora facile osservare come sia ottenibile da , infatti: Si noti come la funzione di dettaglio , negli intervalli di continuità di essere sempre proporzionale ad un’onda di Haar. risulta

Wavelets di Haar Iterando il ragionamento della si può esprimere in funzione di e così via. L’iterazione si ferma quando si raggiunge il livello di approssimazione più scadente possibile per , che coincide con la funzione costante e pari al valor medio di nell’intervallo compatto considerato. Quindi: con (Può essere scritta in quanto è già stato dimostrato che è una base ortonormale).

Wavelets di Haar Si può osservare, allora, che la esprime proprio che è possibile approssimare sempre meglio al crescere di , al limite, per , ed coincidono. Pertanto è un sistema CONS.

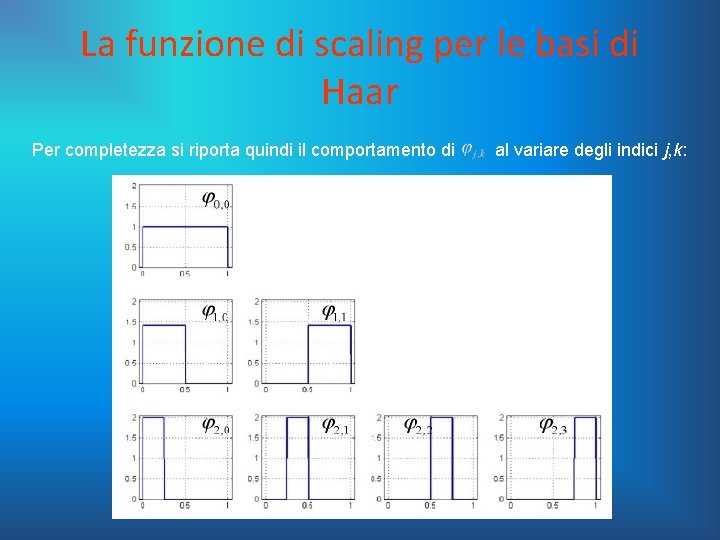
La funzione di scaling per le basi di Haar La funzione di scaling è quella funzione che ci consente di proiettare il segnale da analizzare in uno spazio di un MRA al fine di poterne analizzare il dettaglio mediante una serie wavelet. Se le wavelet adoperate sono quelle di Haar, allora gli spazi dell’MRA sono spazi di funzioni costanti a tratti. La funzione di scaling sarà quindi una funzione costante a tratti, che per generare uno spazio deve essere traslata più volte, mentre per generare l’intero MRA deve essere anche scalata. Per essere precisi una deve godere della seguente proprietà: Alla luce di quanto detto si intuisce che la scelta più semplice che si può fare è la seguente: che può essere traslata e scalata come:

Funzione di approssimazione (Scaling)

Funzione di approssimazione Può essere scalata e traslata come:

La funzione di scaling per le basi di Haar Per completezza si riporta quindi il comportamento di al variare degli indici j, k:

La funzione di scaling per le basi di Haar Risulta chiaro com’è possibile costruire gli spazi le funzioni di scala aventi stesso j. Si può dimostrare che anche l’insieme combinando opportunamente costituisce una base ortonormale.

Trasformata di Fourier e Trasformata Wavelet In altri termini, quanto detto precedentemente, può essere riassunto osservando che lo svantaggio dell’espansione di Fourier è che ha solo risoluzione in frequenza e non nel tempo. Questo significa che sebbene è possibile determinare tutte le frequenze che compongono il segnale, non è possibile tuttavia ricevere alcuna informazione temporale che in qualche modo indichi “quando” una determinata componente frequenziale è comparsa. Per superare questo problema, nel corso della storia della matematica, sono state sviluppate diverse soluzioni capaci più o meno di rappresentare un segnale nel dominio del tempo e della frequenza contemporaneamente. Il principio di indeterminazione di Heisenberg afferma che è impossibile conoscere con esattezza una certa frequenza e l’istante di tempo in cui occorre nel segnale. In altre parole un segnale non può essere semplicemente rappresentato come un punto dello spazio tempo-frequenza.

Trasformata di Fourier e Trasformata Wavelet L’idea che sta alla base delle tecniche di analisi tempo-frequenza consiste nel tagliare il segnale di interesse in differenti parti che verranno analizzate separatamente. E’ chiaro che procedendo per questa strada si intravede la possibilità di localizzare l’occorrenza delle singole componenti frequenziali. Si pone dunque il problema di come tagliare il segnale. La trasformata Wavelet è probabilmente la soluzione più recente in grado di superare le mancanze della trasformata di Fourier. Nell’analisi Wavelet l’uso di una finestra completamente scalabile e adattabile risolve il problema del taglio del segnale. La finestra viene traslata lungo il segnale, e per ogni posizione assunta viene calcolato lo spettro. Tale processo viene iterato con finestre scalate (nella durata) opportunamente. Il risultato finale è una collezione di rappresentazioni tempo-frequenza del segnale tutte di differenti risoluzioni, per questo tale modo di procedere è anche detto analisi multirisoluzione. Le finestre adoperate sono funzioni caratteristiche dell’analisi svolta e vengono chiamate Wavelet, dando così il nome alla trasformata.

Trasformata di Fourier e Trasformata Wavelet Nel caso specifico della trasformata Wavelet non si parla di rappresentazione tempo-frequenza, ma piuttosto tempo-scala ove il termine scala viene utilizzato in luogo di frequenza perché quest’ultimo è riservato all’analisi di Fourier. Il concetto di scala è intimamente legato alla durata delle finestre adoperate. Le analisi effettuate su larga scala equivarranno a studi di basse frequenze, viceversa analisi in piccola scala equivarranno a studi localizzati di alte frequenze (studio in dettaglio). Volendo evidenziare i vantaggi della trasformata Wavelet si ricorre allo studio dei segnali mostrati nei precedenti due esempi.

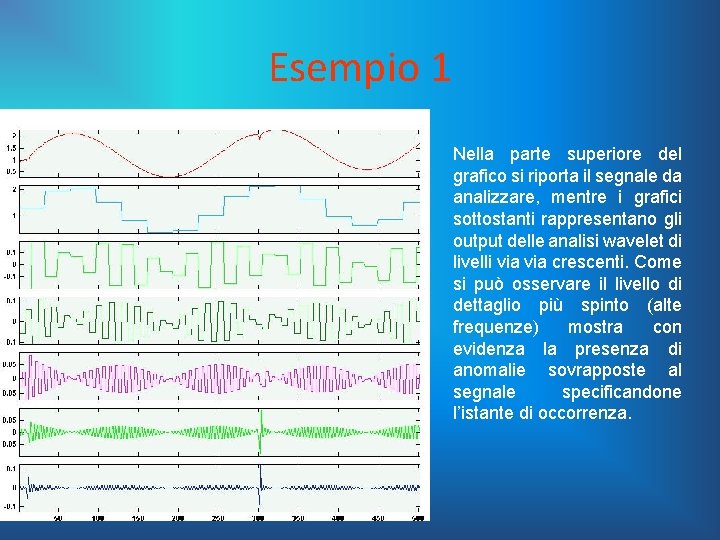
Esempio 1 Nella parte superiore del grafico si riporta il segnale da analizzare, mentre i grafici sottostanti rappresentano gli output delle analisi wavelet di livelli via crescenti. Come si può osservare il livello di dettaglio più spinto (alte frequenze) mostra con evidenza la presenza di anomalie sovrapposte al segnale specificandone l’istante di occorrenza.

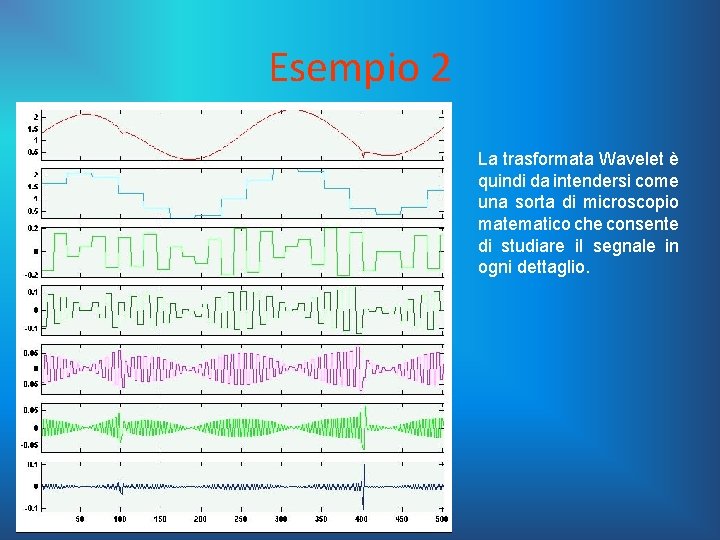
Esempio 2 La trasformata Wavelet è quindi da intendersi come una sorta di microscopio matematico che consente di studiare il segnale in ogni dettaglio.

Esempio Si premette che si opererà su segnali di tipo digitale, vale a dire definiti per istanti di tempi discreti e a valori discreti. Quando si effettua una trasformata wavelet su un segnale digitale si dice che si effettua la trasformata wavelet discreta, detta anche DWT. Senza voler approfondire l’argomento sui segnali digitali diciamo soltanto che essi presentano uno spettro di frequenze periodico, il cui periodo è legato alla frequenza di campionamento del segnale. Si intuisce che non ha senso spingere i livelli di dettaglio delle wavelet oltre un certo limite. In realtà non è proprio possibile andare oltre un certo livello di dettaglio. Osserviamo infatti che se discretizziamo le wavelet di Haar, l’onda più piccola che si riesce ad ottenere presenta un supporto di due campioni di cui il secondo è l’opposto del primo. È questo il livello massimo di dettaglio che si riesce ad ottenere. Ora, se si considera come wavelet madre un’onda che ha il supporto pari proprio alla durata del segnale, si osserva che il massimo valore che si può dare a j è:

Esempio Siccome j deve essere necessariamente un numero intero si adopera la formula: Per ragioni che trovano spiegazione nella storia della trasformata wavelet, il tool Matlab si basa su una diversa interpretazione dell’indice j. Si è detto fino ad ora che all’aumentare di j si spinge l’analisi verso dettagli più accurati. In Matlab è l’esatto opposto; si indica con j=1 il massimo livello di dettaglio che si può raggiungere e per j crescente si riduce l’accuratezza. Allora la relazione scritta esprime il massimo numero di livelli analizzabile.

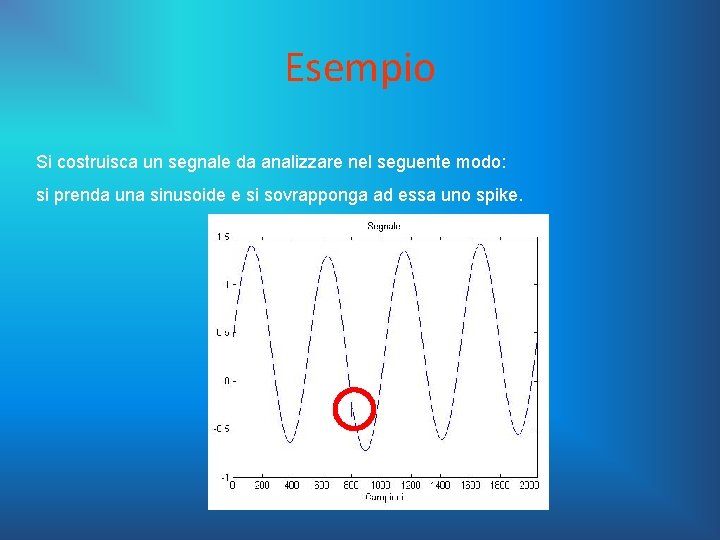
Esempio Si costruisca un segnale da analizzare nel seguente modo: si prenda una sinusoide e si sovrapponga ad essa uno spike.

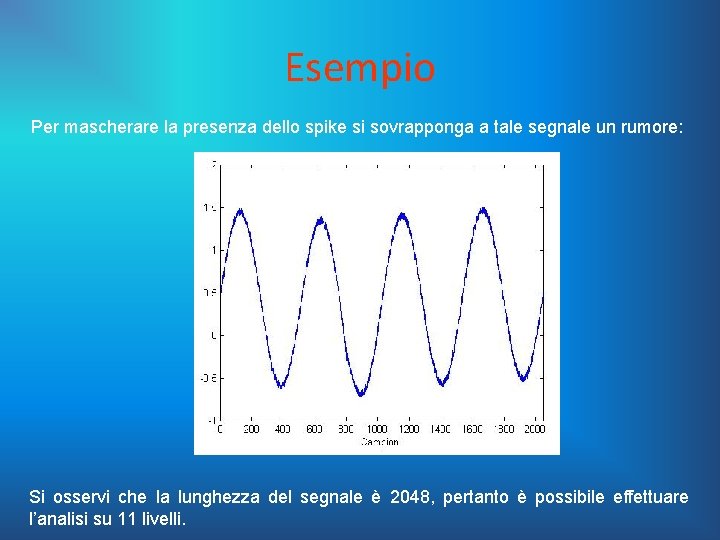
Esempio Per mascherare la presenza dello spike si sovrapponga a tale segnale un rumore: Si osservi che la lunghezza del segnale è 2048, pertanto è possibile effettuare l’analisi su 11 livelli.

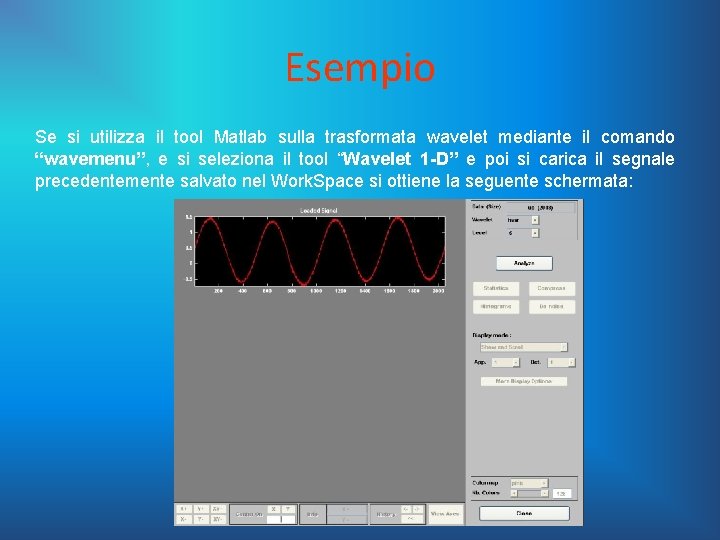
Esempio Se si utilizza il tool Matlab sulla trasformata wavelet mediante il comando “wavemenu”, e si seleziona il tool “Wavelet 1 -D” e poi si carica il segnale precedentemente salvato nel Work. Space si ottiene la seguente schermata:

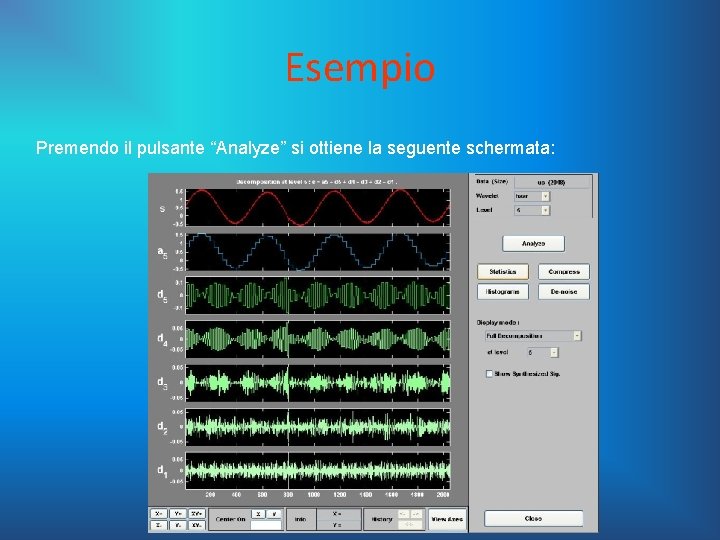
Esempio Premendo il pulsante “Analyze” si ottiene la seguente schermata:

Esempio Come si può notare in alto compare la scritta: s=a 5+d 4+d 3+d 2+d 1 Significa che il segnale approssimato al livello 5 è a 5, mentre i segnali d 5 -d 1 sono i dettagli che mancano per ricostruire esattamente il segnale. Come si può notare, nonostante la presenza del rumore, si nota la presenza di un’anomalia nell’intorno dell’ottocentesimo campione. Più preciso è il livello di dettaglio è più è evidente la presenza dell’anomalia.

Esempio Selezionando la voce “Tree Mode” dal menù a tendina “Display Mode” è possibile capire meglio come viene analizzato e sintetizzato il segnale: A partire dal segnale s e sottraendo il segnale di dettaglio d 1 si ottiene l’approssimazione a 1. Da questa è possibile sottrarre il segnale di dettaglio d 2 ottenendo l’approssimazione a 2 e così via. Cliccando sulle lettere è possibile visualizzare i segnali di interesse. Nella figura compaiono il segnale ed il dettaglio di livello 1 per evidenziare ulteriormente la presenza dell’anomalia.

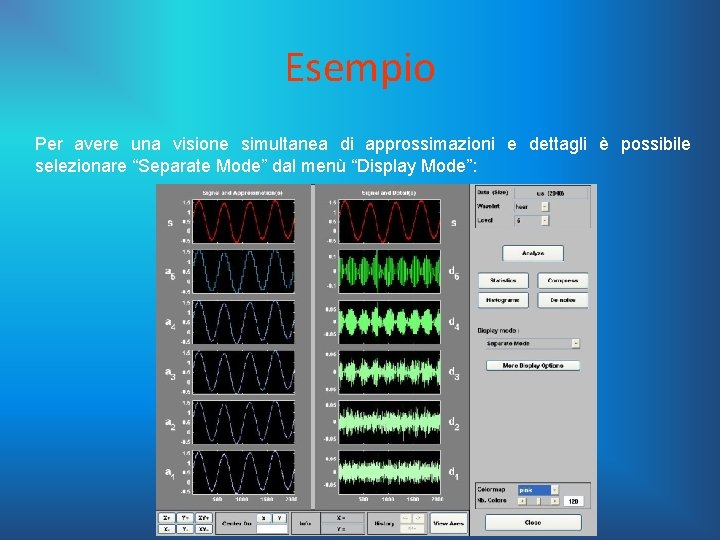
Esempio Per avere una visione simultanea di approssimazioni e dettagli è possibile selezionare “Separate Mode” dal menù “Display Mode”:

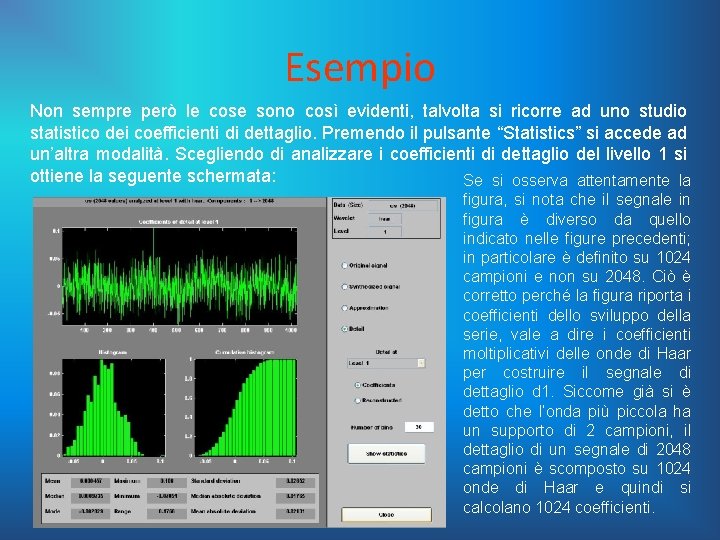
Esempio Non sempre però le cose sono così evidenti, talvolta si ricorre ad uno studio statistico dei coefficienti di dettaglio. Premendo il pulsante “Statistics” si accede ad un’altra modalità. Scegliendo di analizzare i coefficienti di dettaglio del livello 1 si ottiene la seguente schermata: Se si osserva attentamente la figura, si nota che il segnale in figura è diverso da quello indicato nelle figure precedenti; in particolare è definito su 1024 campioni e non su 2048. Ciò è corretto perché la figura riporta i coefficienti dello sviluppo della serie, vale a dire i coefficienti moltiplicativi delle onde di Haar per costruire il segnale di dettaglio d 1. Siccome già si è detto che l’onda più piccola ha un supporto di 2 campioni, il dettaglio di un segnale di 2048 campioni è scomposto su 1024 onde di Haar e quindi si calcolano 1024 coefficienti.

Esempio Dall’analisi statistica risulta che il massimo del segnale è molto diverso dalla media e non è contenuto nell’intervallo media +/- deviazione standard. E’ facile intuire che questa situazione è causata proprio dallo spike sovrapposto. La DWT è quindi un potente mezzo di indagine dei segnali, si è infatti riusciti ad individuare un’anomalia mascherata dal rumore. Elaborando ulteriormente i dati della DWT è possibile introdurre molte caratteristiche del segnale. Un’ulteriore analisi potrebbe essere quella di misurare l’entropia di ogni livello di dettaglio. In questo modo si hanno informazioni circa la presenza di irregolarità in ogni scala del segnale. Conoscendo la natura del segnale è possibile dare un significato fisico ai valori delle entropie calcolate.