Universit dAdrar Facult des Sciences et de la

Université d’Adrar Faculté des Sciences et de la technologie Département de Math et Informatique 1ème Année Master Informatique Option : System Intelligent Réseau de neurones 2 Partie 1 : Perceptron multicouche Mr. MAMOUNI EL MAMOUN 1

Perceptron (Rappel) • Couche d’entrée : n entrées • Une sortie • La sortie d’un neurone discret peut avoir des valeurs 1 (excité) et 0 (inhibé) • Le neurone a un seuil (threshold). Il s’excite si la somme pondérée des entrées > seuil • Connexion de l’entrée j au neurone i représenté par un poids wij 2

Théorème de convergence de Perceptron • Soit X un ensemble d'apprentissage fini linéairement séparable. • Soit un vecteur des poids initial et un paramètre d'apprentissage α choisit arbitrairement comme une valeur > 0 • Alors pour chaque paire de l'ensemble d'apprentissage de X, le calcul du vecteur de poids au moyen de la règle d'apprentissage du perceptron converge dans un nombre fini de pas. 3

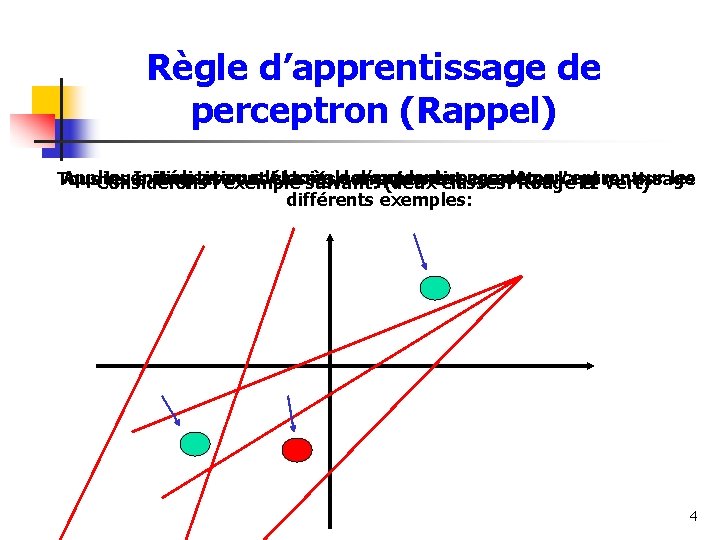
Règle d’apprentissage de perceptron (Rappel) Initialisation aléatoire des poids de perceptron. . . Appliquer itérativement la règle d’apprentissage de perceptron sur les Tous les exemples sont classés correctement. . . arrêter l'apprentissage Considérons l'exemple suivant: (deux classes: Rouge et Vert) différents exemples: 4

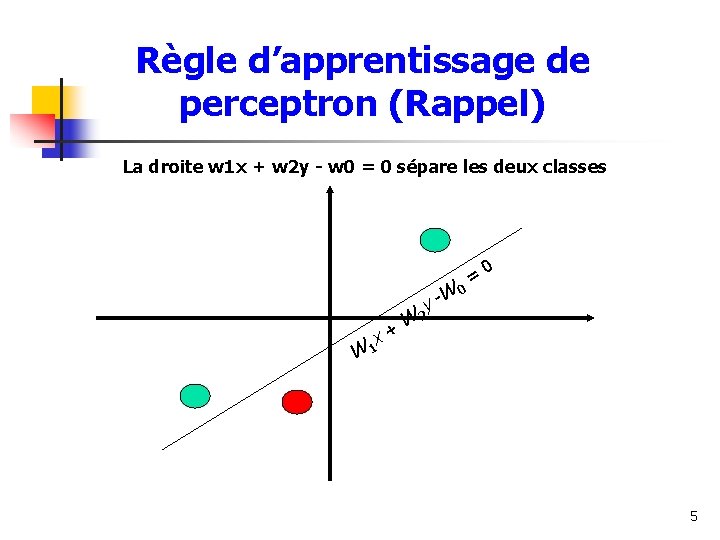
Règle d’apprentissage de perceptron (Rappel) La droite w 1 x + w 2 y - w 0 = 0 sépare les deux classes W y- W + x 1 0 = 0 W 2 5

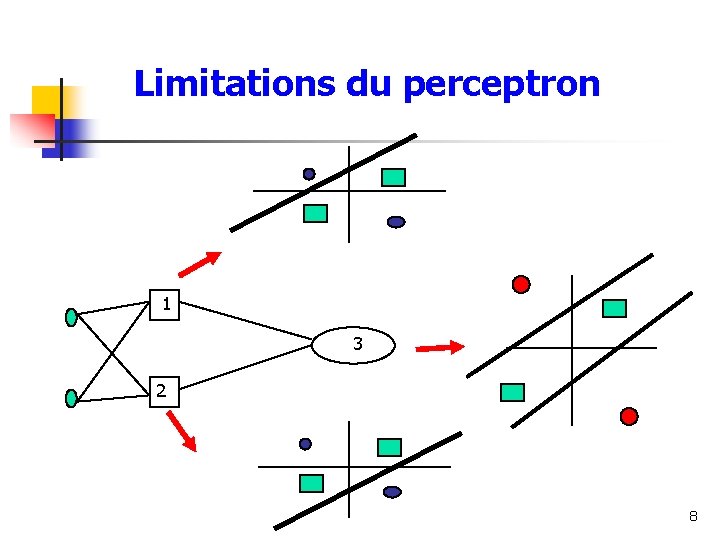
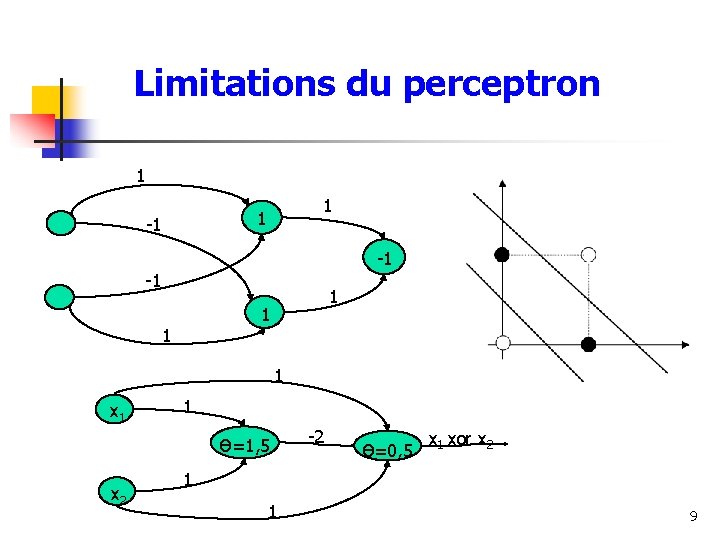
Limitations du perceptron • Dans le cas de la fonction OU-EXCLUSIF, la séparation des deux classes ne peut se faire par une droite E 1 • Un perceptron ne peut construire qu’une frontière linéaire. + – • La majorité des problèmes ne sont pas linéairement séparables E 2 – + « OU-Exc » logique 6

Limitations du perceptron Minsky & Papert (1969) ont proposé une solution au problème XOR en combinant les réponses de l'unité perceptron à l'aide d'une seconde couche d'unités. 7

Limitations du perceptron 1 3 2 8

Limitations du perceptron 1 1 1 -1 -1 -1 1 1 x 1 1 Ɵ=1, 5 x 2 -2 Ɵ=0, 5 x 1 xor x 2 1 1 9

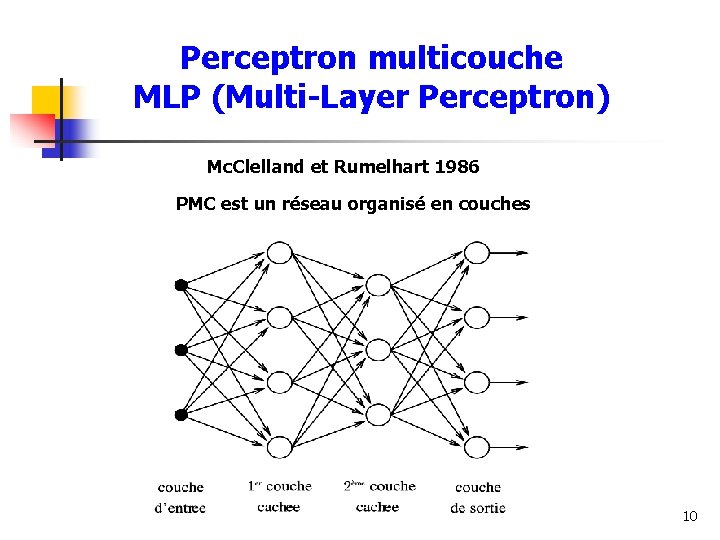
Perceptron multicouche MLP (Multi-Layer Perceptron) Mc. Clelland et Rumelhart 1986 PMC est un réseau organisé en couches 10

Perceptron multicouche MLP (Multi-Layer Perceptron) Propriétés des PMC : • Une couche : un groupe de neurones uniformes sans connexion les uns avec les autres réalise une transformation vectorielle : • Une couche reçoit un vecteur d’entrée et le transforme en vecteur de sortie. • Les dimensions d’entrée et de sortie peuvent être différentes • Structure sans cycle (feed-forward) : une couche ne peut utiliser que les sorties des couches précédentes. 11

Perceptron multicouche MLP (Multi-Layer Perceptron) Propriétés des PMC : • Un PMC a une ou des couches cachées. • Chaque couche a pour entrées les sorties de la couche précédente (couche inférieure). • Les unités d’une couche sont reliées à toutes celles de la couche supérieure. • Les unités des couches cachées ont des fonctions d'activations non-linéaires. • Un PMC peut approximer tous les problèmes de classifications non-linéaires. 12

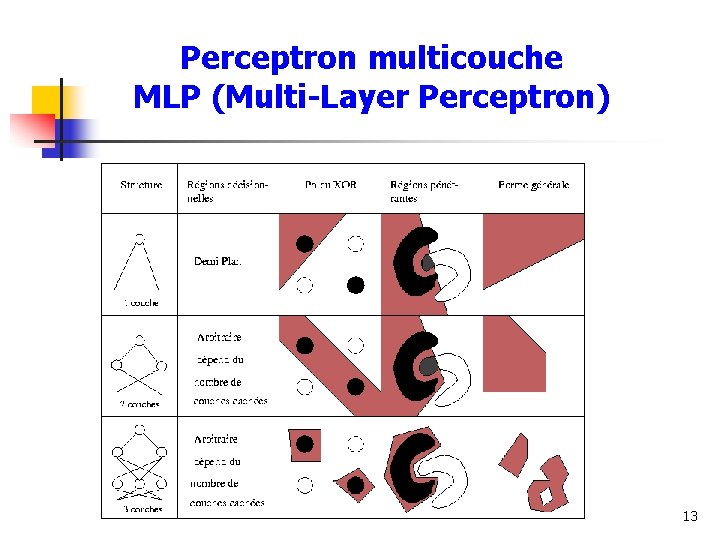
Perceptron multicouche MLP (Multi-Layer Perceptron) 13

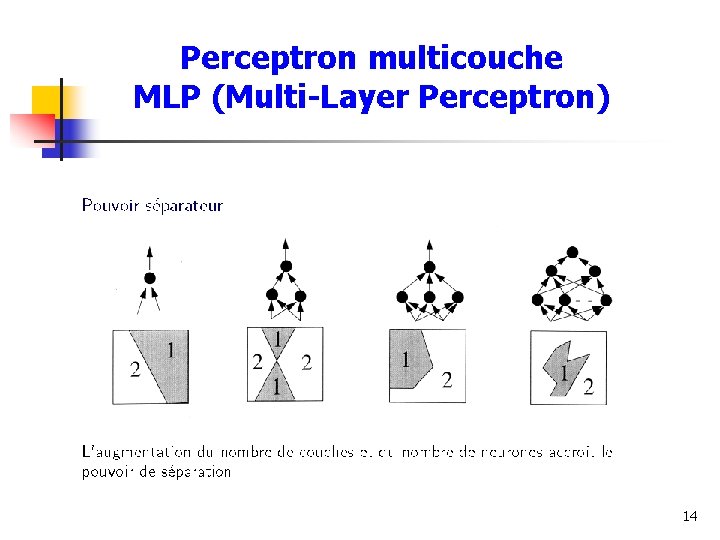
Perceptron multicouche MLP (Multi-Layer Perceptron) 14

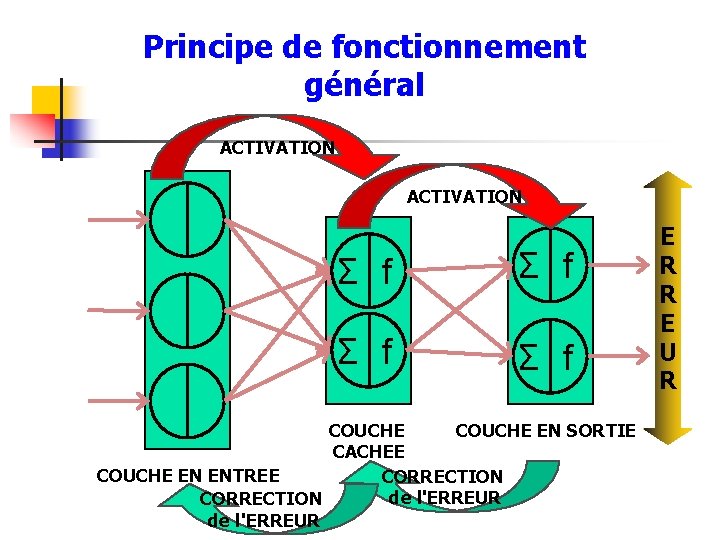
Principe de fonctionnement général ACTIVATION Σ f Σ f COUCHE EN SORTIE CACHEE COUCHE EN ENTREE CORRECTION de l'ERREUR E R R E U R

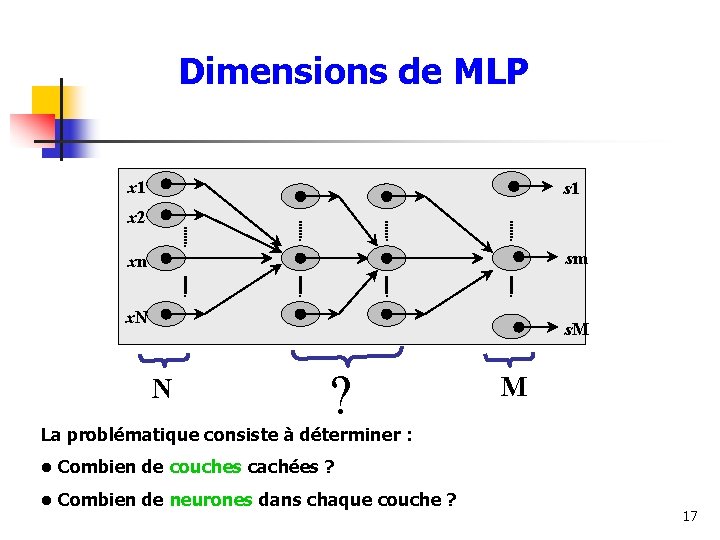
Dimensions de MLP x 1 s 1 x 2 sm xn x. N s. M N ? M La problématique consiste à déterminer : • Combien de couches cachées ? • Combien de neurones dans chaque couche ? 17

Théorème de Hecht-Nielsen (1987) « Un perceptron à 3 couches comprenant N neurones d'entrée et (2 N+1) neurones cachées utilisant des fonctions nonlinéaires continu peut approximer toute fonction continue de N variables » 18

Quelle est la nature des sorties ? Neurone de Mc. Culloch&Pitts Þ sorties bipolaires +1 et -1 Þ sorties binaires +1 et 0 Comment associer une sortie à chaque classe ? Classe « m » : X Cm sm=1, et sm’=0 si m m’ 19

Comment réaliser l’apprentissage des poids synaptiques ? Algorithme du gradient Fonctions « dérivables » Donc on doit utiliser une fonction non-linéaire pour l’activation sinon le perceptron multicouche se comporterait comme un perceptron linéaire ! 20

Fonctions d’activation • La fonction de sortie sigmoïdale est en quelque sorte la pierre angulaire de l’algorithme de rétro-propagation du gradient d’erreur. • Cette fonction est à la fois suffisamment discriminante pour pouvoir afficher les classes de sortie et à la fois différentiable en tout point afin de pouvoir calculer une valeur de gradient. • De plus, sa forme de type exponentielle permet de calculer facilement sa dérivée car l’exponentielle est la seule fonction dont la dérivée est également une exponentielle. 21

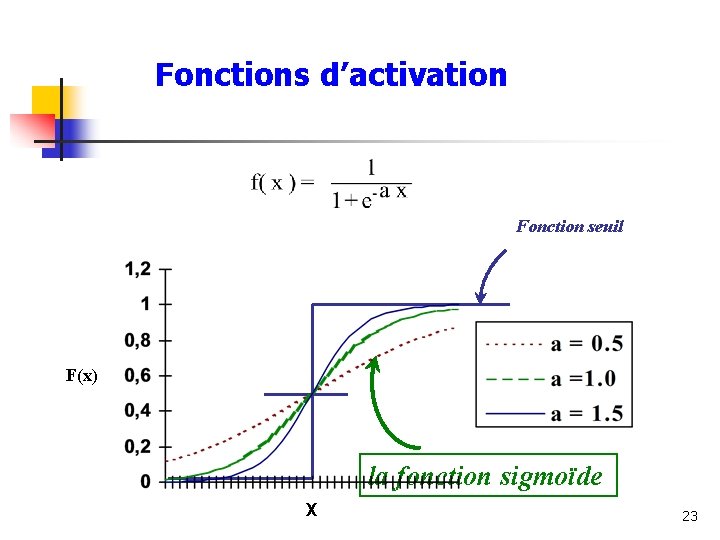
Fonctions d’activation La fonction logistique ou sigmoïde est une fonction non linéaire et dérivable. La fonction sigmoïde (unipolaire): Sigmoïde à pente ajustable : 22

Fonctions d’activation Fonction seuil 1 F(x) 2 3 la fonction sigmoïde X 23

Fonctions d’activation • La fonction logistique (ou sigmoïde) : Sa dérivée : 24

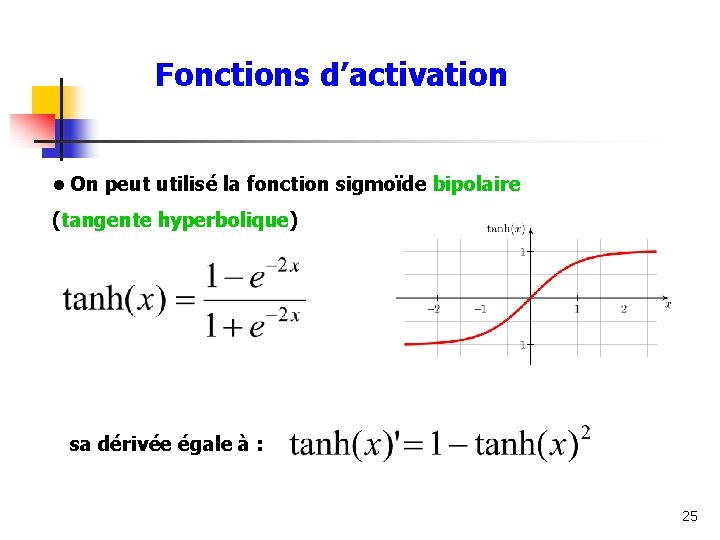
Fonctions d’activation • On peut utilisé la fonction sigmoïde bipolaire (tangente hyperbolique) sa dérivée égale à : 25

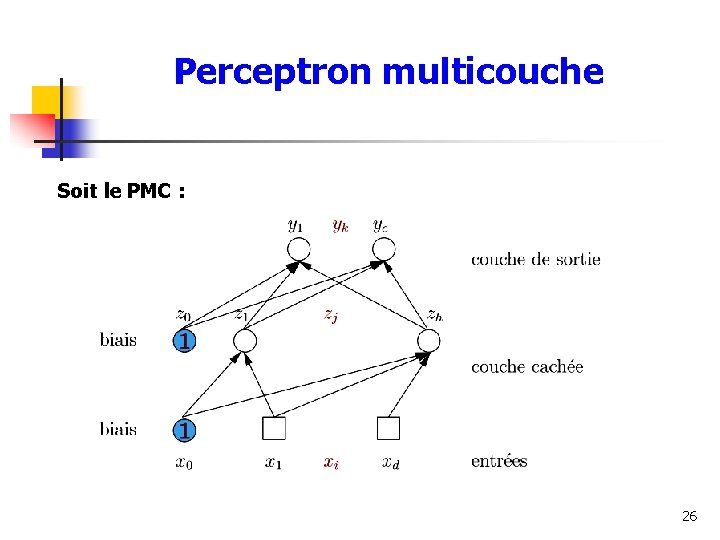
Perceptron multicouche Soit le PMC : 26

La couche cachée Chaque unité cachée j reçoit une activation correspondant à la combinaison linéaire des d entrées. Où ( l ) désigne la lième couche, p le nombre d’unités de la couche précédente, et wji le poids de la connexion allant de i à j. Si l = 1, p = d (nombre d’entrées) 27

La couche cachée • Unité biais x 0: valeur fixée à 1: permet d’intégrer le seuil w 0 dans le vecteur des poids wi • La sortie d’une unité cachée j = transformation non linéaire de l’activation aj par une fonction d’activation f 28

La couche de sortie Nombre d’unités de sortie Régression : 1 unité de sortie représentant la valeur estimée Classification binaire : 1 unité représentant la classe "positive" Classification multi-classes (c > 2) : 1 unité par classe Chaque unité de sortie k reçoit une activation correspondant à la combinaison linéaire des sorties des h unités cachées. 29

La couche de sortie La valeur d’une unité de sortie k = transformation de l’activation ak par une fonction g g peut être différente de f car les unités de sortie et les unités cachées ont des rôles distincts 30

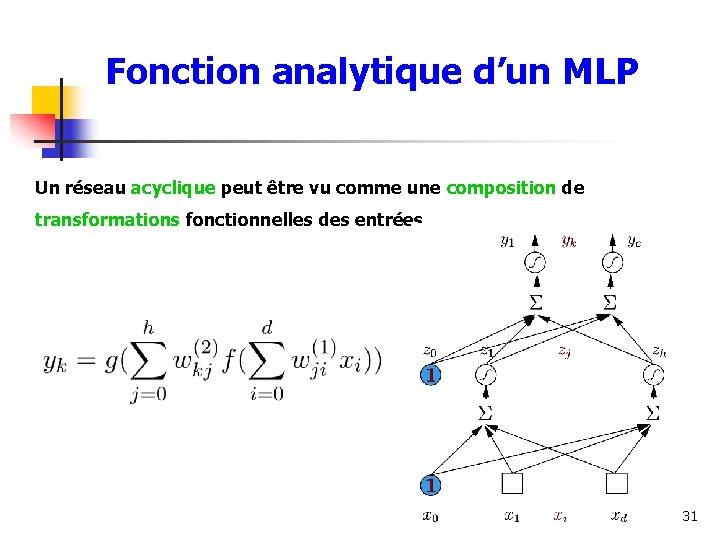
Fonction analytique d’un MLP Un réseau acyclique peut être vu comme une composition de transformations fonctionnelles des entrées 31

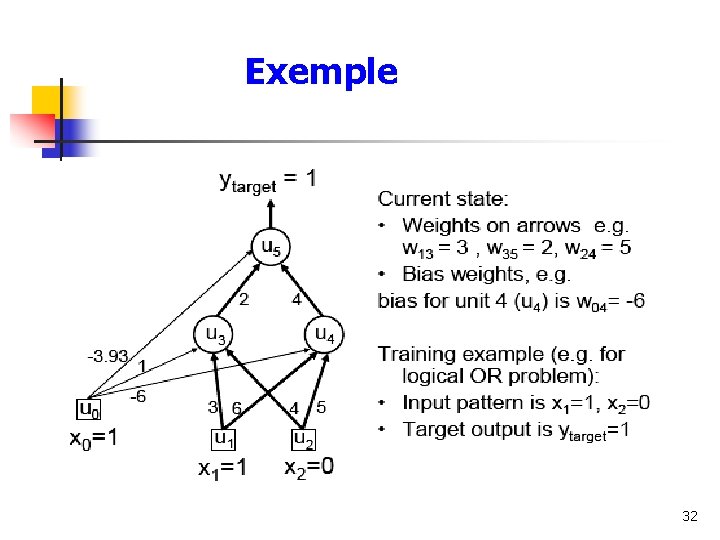
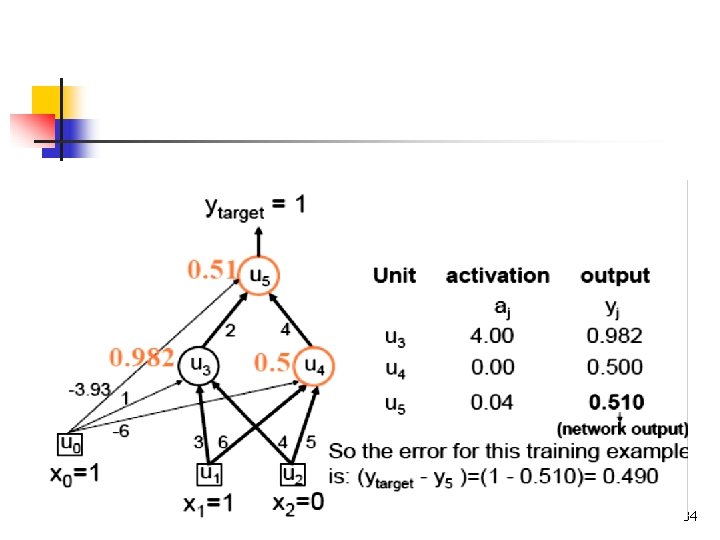
Exemple 32

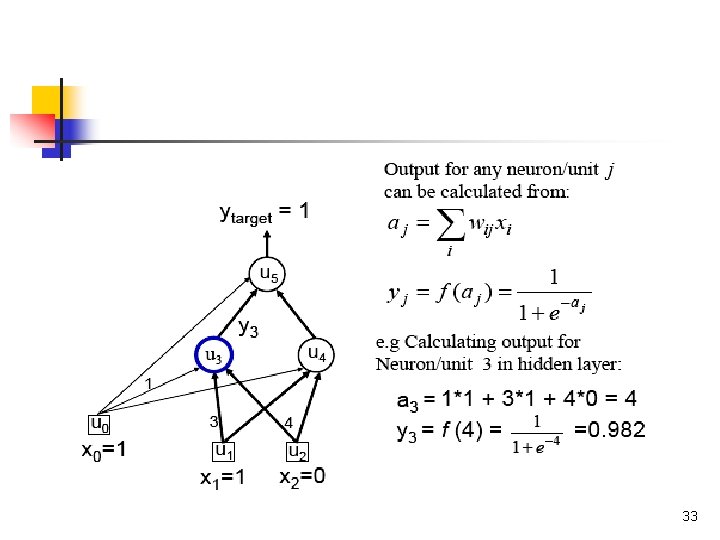
33

34