Universidade Federal de Juiz de Fora UFJF Departamento













- Slides: 22

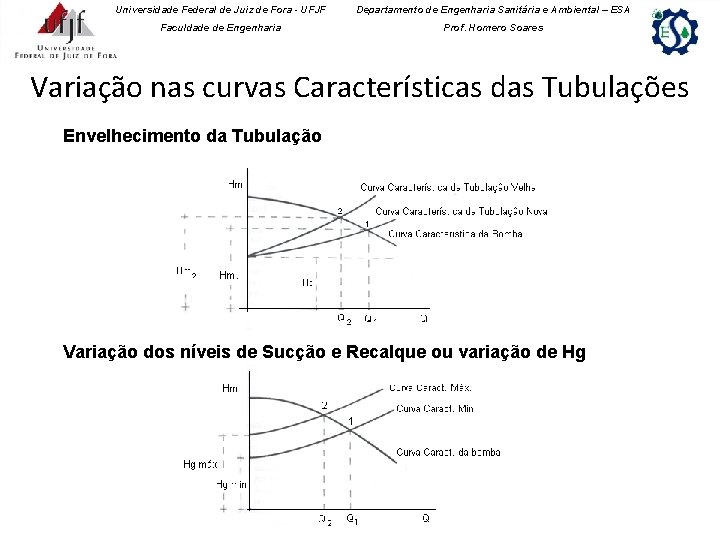
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Variação nas curvas Características das Tubulações Envelhecimento da Tubulação Variação dos níveis de Sucção e Recalque ou variação de Hg

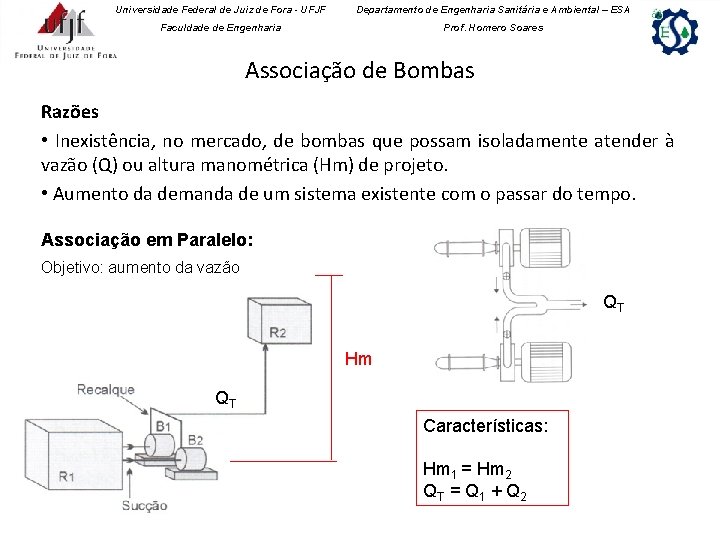
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Associação de Bombas Razões • Inexistência, no mercado, de bombas que possam isoladamente atender à vazão (Q) ou altura manométrica (Hm) de projeto. • Aumento da demanda de um sistema existente com o passar do tempo. Associação em Paralelo: Objetivo: aumento da vazão QT Hm QT Características: Hm 1 = Hm 2 QT = Q 1 + Q 2

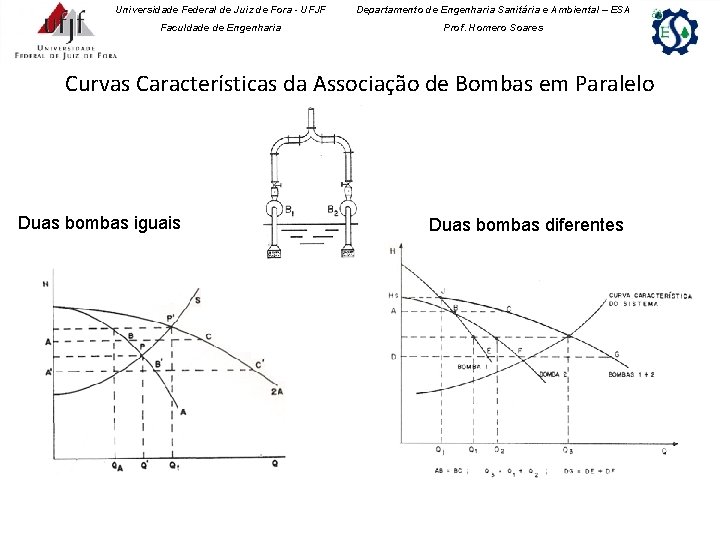
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Curvas Características da Associação de Bombas em Paralelo Duas bombas iguais Duas bombas diferentes

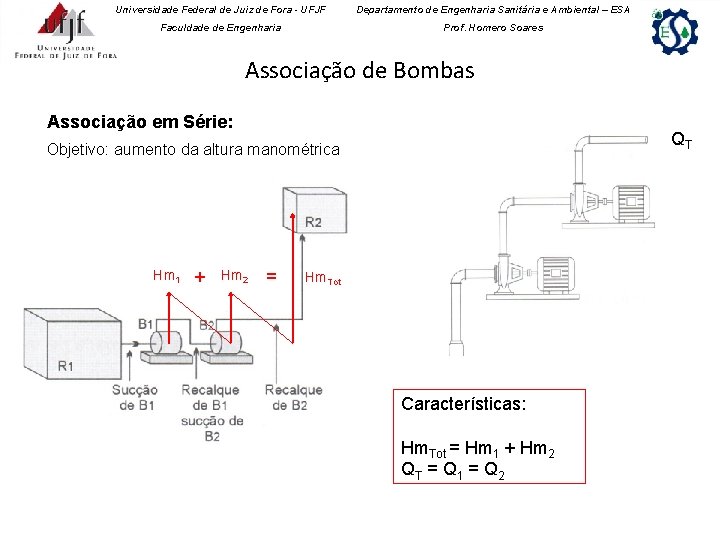
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Associação de Bombas Associação em Série: QT Objetivo: aumento da altura manométrica Hm 1 + Hm 2 = Hm. Tot Características: Hm. Tot = Hm 1 + Hm 2 QT = Q 1 = Q 2

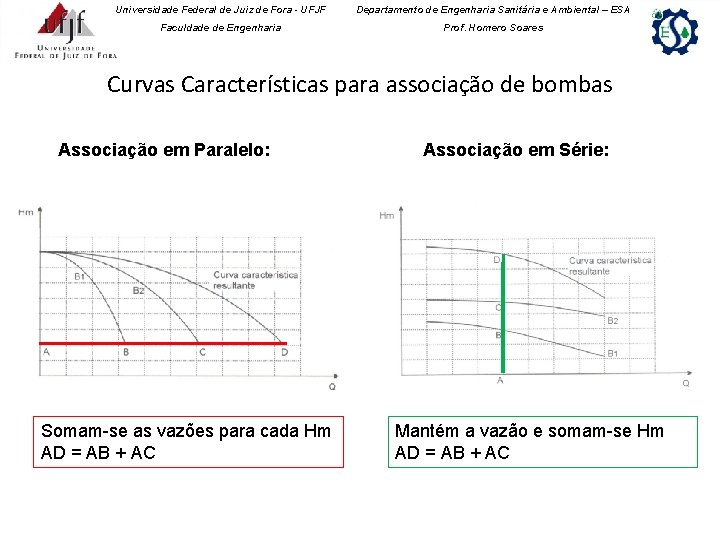
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Curvas Características para associação de bombas Associação em Paralelo: Somam-se as vazões para cada Hm AD = AB + AC Associação em Série: Mantém a vazão e somam-se Hm AD = AB + AC

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Problema V. 4 Uma adutora de 250 mm de diâmetro e 5 km de extensão, cujo coeficiente de atrito vale 0, 02, interliga dois reservatórios cujos desnível entre os NA’s é de 15 m, Conhecendo-se as curvas características da bomba (quadro abaixo), desprezando-se as perdas localizadas, solicita-se o ponto de trabalho Pt(Q, Hm) se duas bombas idênticas à especificada forem instaladas em paralelo e posteriormente forem instaladas em série. Q (m 3/h) 0 50 100 150 200 250 300 350 400 450 500 Hm (m) 80 79 77 73, 8 70 65 59 52 43 35 25

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Problema V. 5 Uma elevatória é projetada para recalcar 500 m 3/h a uma altura manométrica de 30 m através de uma adutora de 400 mm de diâmetro, 12 km de comprimento e coeficiente de perda de carga da Fórmula Universal igual a 0, 022. A perda localizada prevista é de 10 U 2/2 g. Visando aproveitar uma bomba existente, cujas características, à rotação de 1800 rpm, são mostradas no quadro a seguir, pede-se: a) O ponto de trabalho; b) Determine a nova rotação para que a bomba trabalhe exatamente com a vazão de projeto. Q (m 3/h) 0 100 200 300 400 500 600 Hm (m) 120 119 115 109 100 87 70

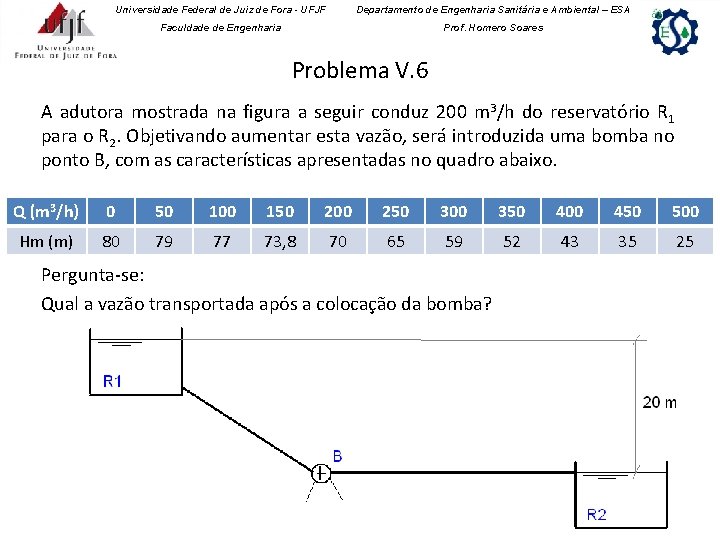
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Problema V. 6 A adutora mostrada na figura a seguir conduz 200 m 3/h do reservatório R 1 para o R 2. Objetivando aumentar esta vazão, será introduzida uma bomba no ponto B, com as características apresentadas no quadro abaixo. Q (m 3/h) 0 50 100 150 200 250 300 350 400 450 500 Hm (m) 80 79 77 73, 8 70 65 59 52 43 35 25 Pergunta-se: Qual a vazão transportada após a colocação da bomba?

Universidade Federal de Juiz de Fora - UFJF Faculdade de Engenharia Departamento de Engenharia Sanitária e Ambiental – ESA Prof. Homero Soares

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Cavitação Natureza do Fenômeno • As tubulações de sucção de instalações de recalque normalmente funcionam com pressões inferiores à pressão atmosférica. • Se na entrada da bomba existem pressões inferiores à pressão de vapor do líquido, poderão formar-se bolhas de vapor que podem ser prejudiciais ao funcionamento e à vida útil das bombas. Características do Fenômeno • Formação de bolhas no líquido devido à redução de pressão ao nível de pressão de vapor do líquido (processo semelhante à fervura). • Fervura: vaporização com temperatura crescente e pressão constante. • Cavitação: vaporização (fervura) com temperatura constante e pressão decrescente.

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Conseqüências da Cavitação: -Interrupção na circulação do líquido; - Ruídos internos; -Vibrações; -Queda de rendimento da bomba; -Danos na carcaça e rotor da bomba. Condições para se evitar a Cavitação: - Para que uma bomba trabalhe sem cavitar, torna-se necessário que a pressão absoluta do líquido na entrada da bomba seja superior à pressão de vapor, na temperatura de escoamento do fluido. Fatores intervenientes na Cavitação: -Altura de sucção; -Rugosidade das paredes da tubulação; -Temperatura do fluido.

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Altura Máxima de Sucção: -Aplicando Bernoulli entre o ponto “ 0” na superfície do reservatório e o ponto “ 1” dentro da bomba antes do rotor conforme mostra a figura a seguir; - O ponto “ 1” é o de menor pressão dentro da instalação elevatória. É justamente o ponto onde podem surgir bolhas microscópicas que podem originar a cavitação. Se hs ≤ 0 Bomba afogada não há pressões menores que a atmosférica no tubo de sucção. Se hs > 0 É preciso analisar. Passando o “Datum” pelo ponto “ 0”. hfs – Perda de carga na tubulação de sucção. hs – Altura de sucção; ∆h – Perda de carga que ocorre entre o final do tubo de sucção e a entrada do rotor. Assim fica:

Assim: Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares OBS: Se fosse possível desprezar as perdas de carga e a diferença de energias cinéticas, a altura estática de sucção valeria. hsmáx = 10 mca Este seria o valor teórico máximo da altura estática de sucção, ao nível do mar operando com água fria (4ºC). Na prática este valor situa-se em torno de 6 a 8 metros, pois a parcela entre colchetes na expressão de “hsmáx” deverá ser sempre maior do que zero. OBS: “hsmáx” é o valor máximo da altura de sucção a partir da qual há formação de bolhas de vapor. 1º) Somente tem valor positivo, mostrando que a mesma facilita a sucção; 2º) As demais parcelas, de sinal negativo, dificultam a sucção.

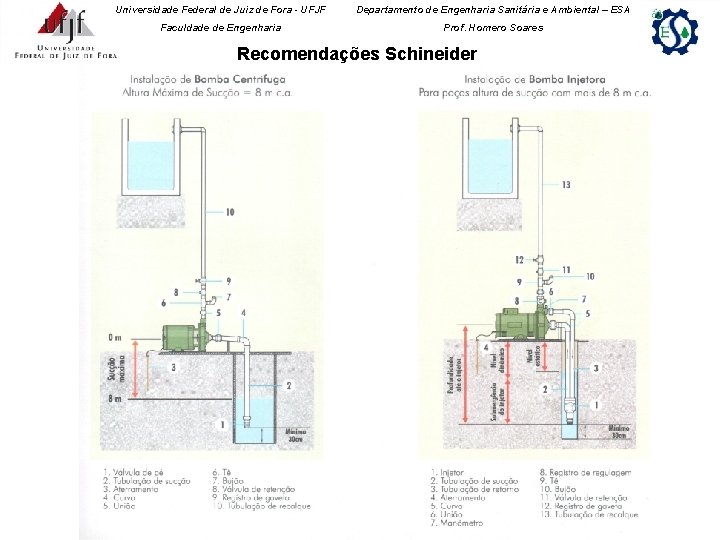
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Homero Soares Recomendações Schineider

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro -Outra forma de interpretar a cavitação é separar na equação os termos que dependem da instalação ou do líquido bombeado, dos termos que dependem da bomba. Variáveis que dependem da máquina (bomba) Variáveis que dependem das condições locais de instalação de sucção e do líquido PRIMEIRO MEMBRO Instalação ou líquido É a soma de todas as grandezas que facilitam (sinal positivo e dificultam (sinal negativo) a sucção da bomba. É carga residual disponível na instalação para a sucção do fluido. É calculado e representa a carga existente na istalação para permitir a sucção do fluido. SEGUNDO MEMBRO Bomba É a carga exigida pela bomba para aspirar o fluido do poço de sucção. É fornecido pelo fabricante e representa a carga energética que a bomba necessita para succionar a água sem cavitar.

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Análise: NPSHDisp > NPSHReq Não há cavitação NPSHDisp < NPSHReq Há cavitação Valor aproximado de NPSHr ≈ 0, 0012 n 4/3. Q 2/3 Onde: n = rpm da bomba Q = vazão (m 3/s) Margem de segurança NPSHd ≥ 1, 2 NPSHr Devido à presença de impurezas no líquido que podem alterar a pressão na qual a cavitação atua.

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Problema V. 7 Uma bomba acionada por um motor de 1775 rpm deve operar nas seguintes condições: Q = 800 m 3/h Hg = 80 m Pv = 238 kgf/m 2 γH 2 O 20 C = 998, 2 kgf/m 3 Patm Local = 9, 24 mca NPSHr = 3, 6 m hf* = 1, 8 m (perdas na sucção) Pede-se a altura máxima na sucção

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Observações: 1º) A pressão atmosférica local varia (diminui) com a altitude; 2º) O valor aproximado da pressão atmosférica local em função da altitude (válida até 2000 m de altitude) é: a) Patm = (760 – 0, 081. h). 13, 6 h = altitude (m) Patm = kgf/m 2 b) Patm = (760 – 0, 081. h). 13, 6 1000 h = altitude (m) Patm = mca

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Problema V. 8 Suponhamos ser de 3 m o NPSHRequerido de certa bomba instalada a 600 m de altitude. Se a água circulante estiver a 65ºC e a perda de carga na sucção for de 1, 5 m, qual a altura máxima de sucção? Dados: Pv (65ºC) = 2550 kgf/m 2 γH 2 O (65ºC) = 981 kgf/m 3

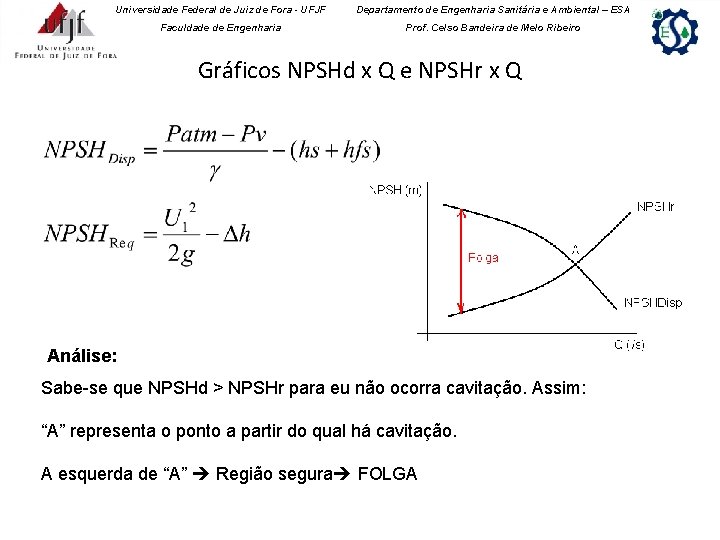
Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Gráficos NPSHd x Q e NPSHr x Q Análise: Sabe-se que NPSHd > NPSHr para eu não ocorra cavitação. Assim: “A” representa o ponto a partir do qual há cavitação. A esquerda de “A” Região segura FOLGA

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Problema V. 9 A bomba mostrada esquematicamente na figura que segue, deve recalcar 30 m 3/h com rotação de 1750 rpm e para essa vazão, o vaor de NPSHr = 2, 50 m (fornecido pelo fabricante). A instalação está na cota 834, 50 m (altitude). A temperatura média de água é 20ºC. Determinar o valor do comprimento “x” para que a “folga” entre o NPSHDisponível e o requerido seja 3, 80 m. Dados: Diâmetro da tubulação de sucção = 75 mm Coeficiente de perda de carga (Hazen Willians) C = 150 (PVC) Válvula de pé com crivo e Joelho 90 º na sucção.

Universidade Federal de Juiz de Fora - UFJF Departamento de Engenharia Sanitária e Ambiental – ESA Faculdade de Engenharia Prof. Celso Bandeira de Melo Ribeiro Problema V. 10 Determinar a vazão máxima permissível de uma bomba para que não haja cavitação, sabendo-se que deve operar em um sistema cujo nível de água no reservatório de sucção está 4, 0 m abaixo do eixo da bomba. Os dados da instalação e a curva de variação do NPSHr desta bomba em relação à vazão são apresentados a seguir: Patm absoluta no local da instalação: 9045 kgf/m 2 Temp. água: 20ºC, γH 2 O = 978, 9 kgf/m 3 Dsucção: 400 mm f = 0, 025 Comprimento da tubulação de sucção = 100 m Peças e acessórios da sucção: - Válv. De pé com crivo - Curva 90º - Redução excêntrica Curva NPSHR x Q Q (m 3/s) 0 0, 02 0, 04 0, 08 0, 12 0, 14 0, 16 0, 18 0, 22 NPSHR (m) 1, 55 1, 65 1, 8 2, 1 2, 35 2, 6 3, 0 3, 35 3, 7 4, 3