UNIVERSIDAD NACIONAL Optaciano Vasquez SANTIAGO ANTNEZ DE MAYOLO

UNIVERSIDAD NACIONAL Optaciano Vasquez “SANTIAGO ANTÚNEZ DE MAYOLO” FACULTAD DE INGENIERÍA CIVIL CURSO: FISICA I DINAMICA DE UNCUERPO RIGIDO AUTOR: Mag. Optaciano L. Vásquez García HUARAZ - PERÚ 2010

I. OBJETIVOS Al finalizar este capítulo el estudiante será capaz de: • Aplicar métodos para calcular momentos de inercia de cuerpos rígidos • Formular las ecuaciones de movimiento para un cuerpo rígido • Aplicar las ecuaciones de movimiento para estudiar el movimiento de traslación de un CR, la rotación de un CR alrededor de un eje fijo y el movimiento plano de un CR

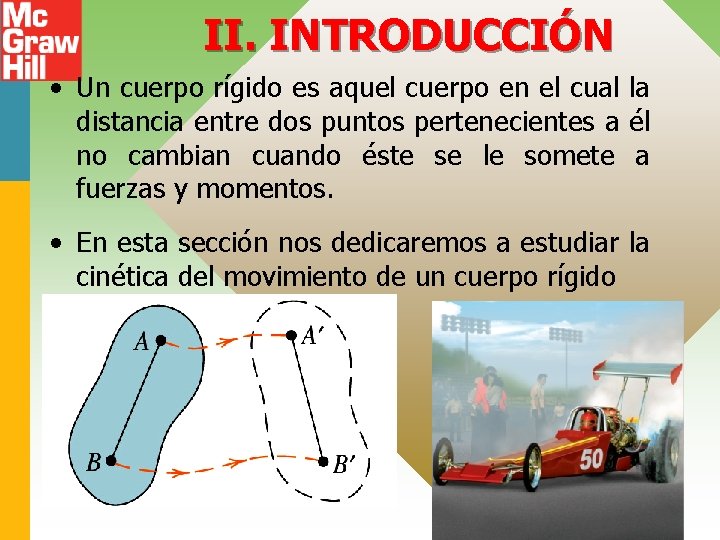
II. INTRODUCCIÓN • Un cuerpo rígido es aquel cuerpo en el cual la distancia entre dos puntos pertenecientes a él no cambian cuando éste se le somete a fuerzas y momentos. • En esta sección nos dedicaremos a estudiar la cinética del movimiento de un cuerpo rígido

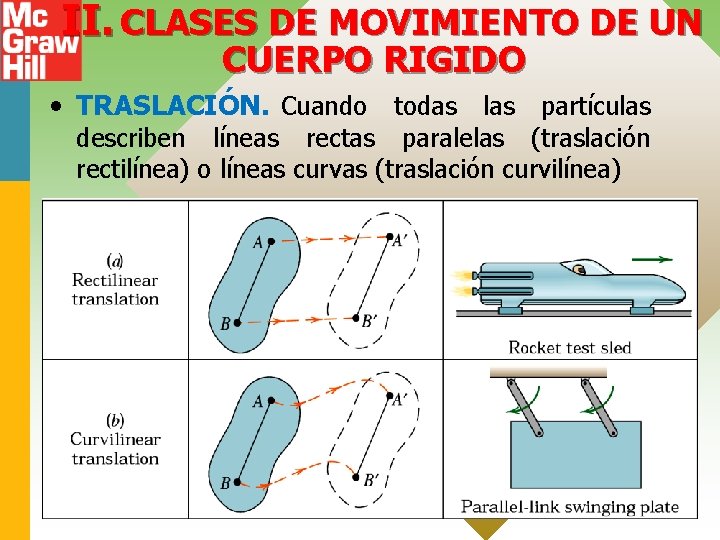
II. CLASES DE MOVIMIENTO DE UN CUERPO RIGIDO • TRASLACIÓN. Cuando todas las partículas describen líneas rectas paralelas (traslación rectilínea) o líneas curvas (traslación curvilínea)

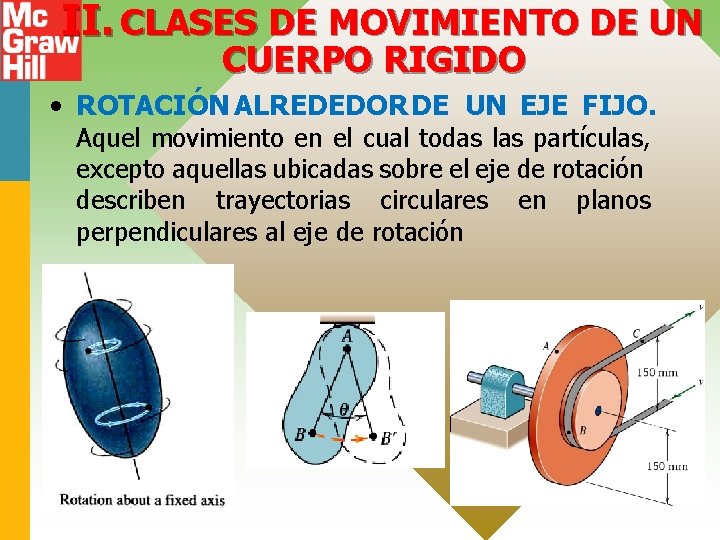
II. CLASES DE MOVIMIENTO DE UN CUERPO RIGIDO • ROTACIÓN ALREDEDOR DE UN EJE FIJO. Aquel movimiento en el cual todas las partículas, excepto aquellas ubicadas sobre el eje de rotación describen trayectorias circulares en planos perpendiculares al eje de rotación

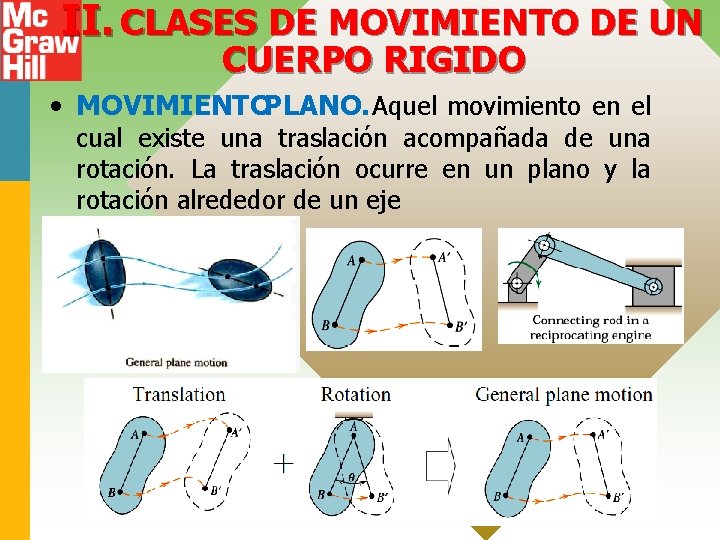
II. CLASES DE MOVIMIENTO DE UN CUERPO RIGIDO • MOVIMIENTOPLANO. Aquel movimiento en el cual existe una traslación acompañada de una rotación. La traslación ocurre en un plano y la rotación alrededor de un eje

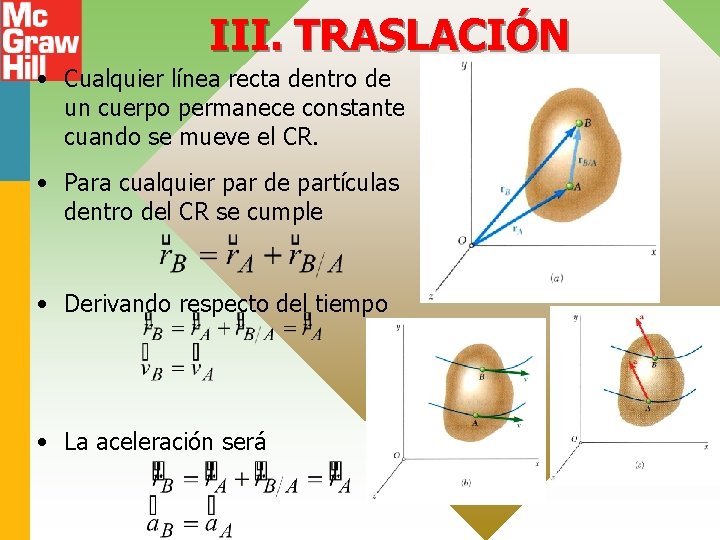
III. TRASLACIÓN • Cualquier línea recta dentro de un cuerpo permanece constante cuando se mueve el CR. • Para cualquier par de partículas dentro del CR se cumple • Derivando respecto del tiempo • La aceleración será

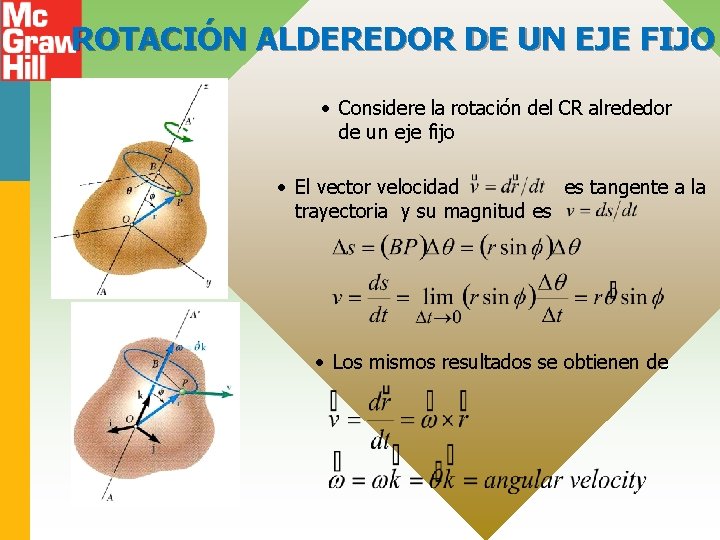
ROTACIÓN ALDEREDOR DE UN EJE FIJO • Considere la rotación del CR alrededor de un eje fijo • El vector velocidad es tangente a la trayectoria y su magnitud es • Los mismos resultados se obtienen de 15 - 8

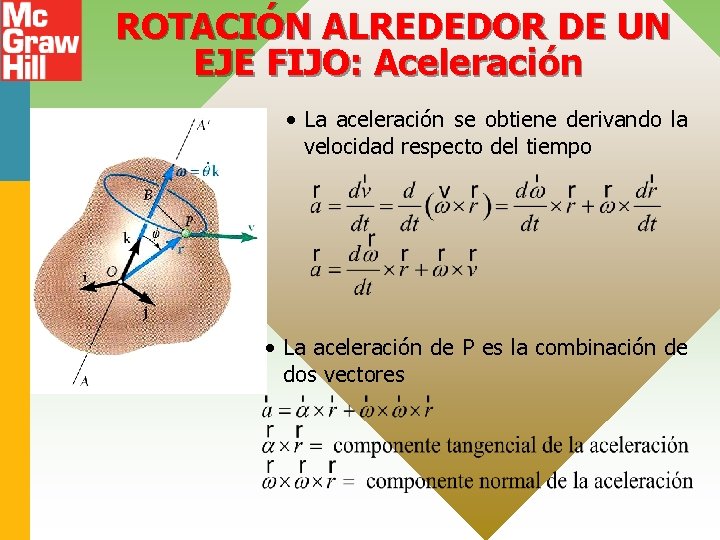
ROTACIÓN ALREDEDOR DE UN EJE FIJO: Aceleración • La aceleración se obtiene derivando la velocidad respecto del tiempo • La aceleración de P es la combinación de dos vectores

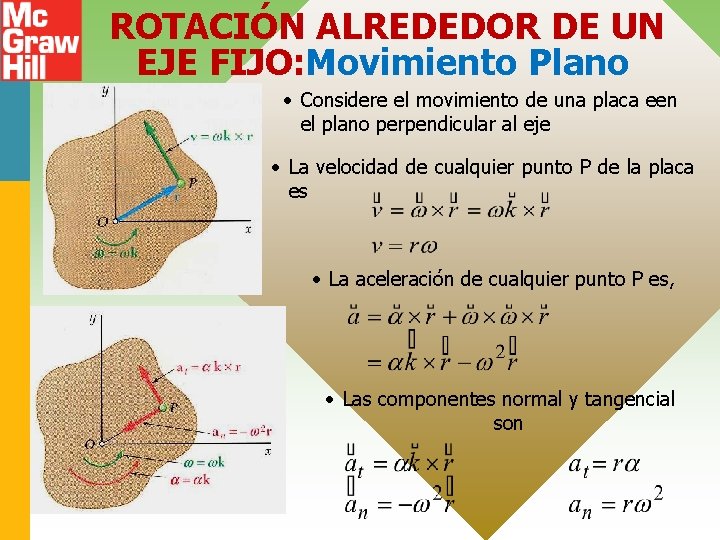
ROTACIÓN ALREDEDOR DE UN EJE FIJO: Movimiento Plano • Considere el movimiento de una placa een el plano perpendicular al eje • La velocidad de cualquier punto P de la placa es • La aceleración de cualquier punto P es, • Las componentes normal y tangencial son 15 - 10

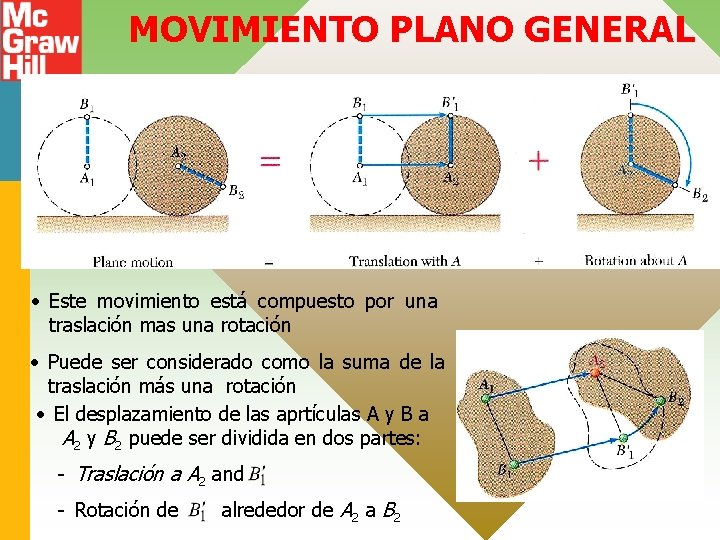
MOVIMIENTO PLANO GENERAL • Este movimiento está compuesto por una traslación mas una rotación • Puede ser considerado como la suma de la traslación más una rotación • El desplazamiento de las aprtículas A y B a A 2 y B 2 puede ser dividida en dos partes: - Traslación a A 2 and - Rotación de alrededor de A 2 a B 2

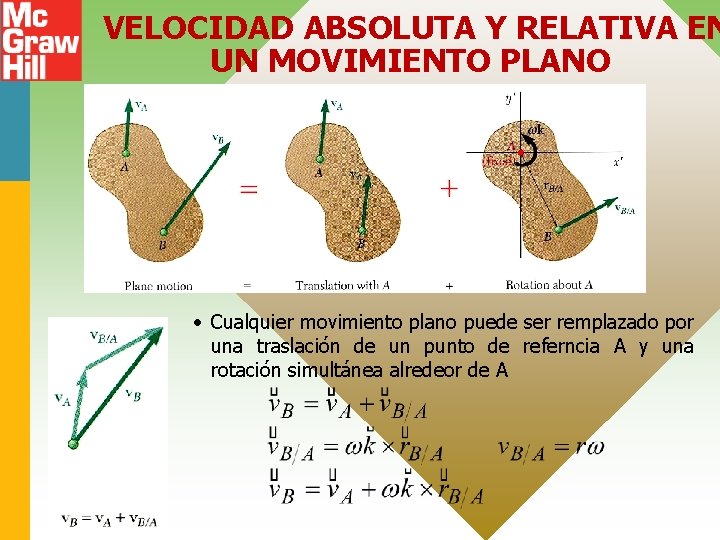
VELOCIDAD ABSOLUTA Y RELATIVA EN UN MOVIMIENTO PLANO • Cualquier movimiento plano puede ser remplazado por una traslación de un punto de referncia A y una rotación simultánea alredeor de A 15 - 12

CENTRO INSTANTÁNEO EN UN MOVIMIENTO PLANO • Todas las partículas de una placa con movimiento plano pueden ser remplazadas por la traslación de cualquier punto arbitrario A y una rotación alrededor de A con una velocidad angular que es independiente del punto elegido • Las mismas velcoidades de traslación y rotación en A pueden ser obtenidas haciendo rotar a la lamina alrededor de C sobre la perpendicular a la velocidad de C • Las velocidades de las demás partículas de la lámina son las mismas que las definidas originalmente 15 - 13 • Por consiguiente, en lo que se refiere a las velocidadesde la placaparecerotaralrededordel centro instantáneo C en el instante considerado

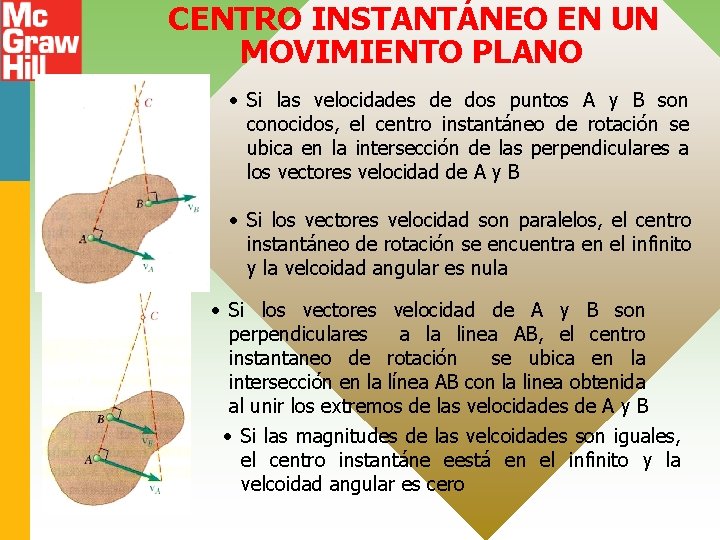
CENTRO INSTANTÁNEO EN UN MOVIMIENTO PLANO • Si las velocidades de dos puntos A y B son conocidos, el centro instantáneo de rotación se ubica en la intersección de las perpendiculares a los vectores velocidad de A y B • Si los vectores velocidad son paralelos, el centro instantáneo de rotación se encuentra en el infinito y la velcoidad angular es nula • Si los vectores velocidad de A y B son perpendiculares a la linea AB, el centro instantaneo de rotación se ubica en la intersección en la línea AB con la linea obtenida al unir los extremos de las velocidades de A y B • Si las magnitudes de las velcoidades son iguales, el centro instantáne eestá en el infinito y la velcoidad angular es cero

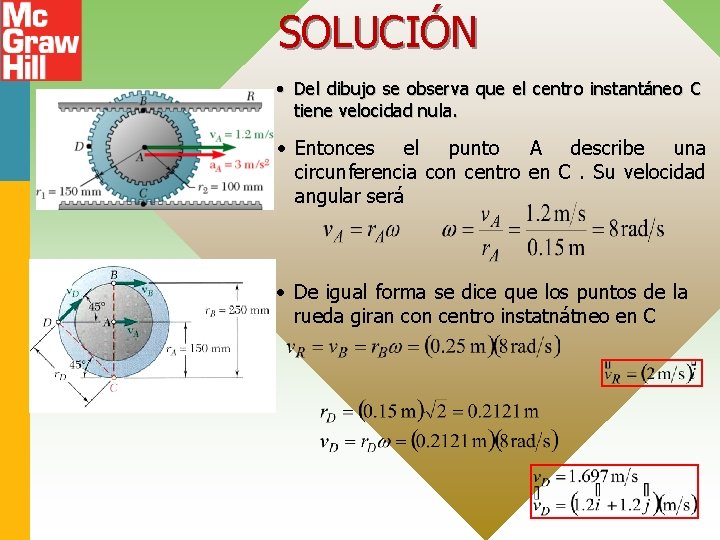
Ejemplo • El doble engranaje de la figura rueda sobre la cremallera inferior que se encuentra. La velocidad de su centro A es de 1, 2 m/s, dirigida hacia la derecha. Determine: (a) la velocidad angular de la rueda dentada, (b) las velocidades de la cremallera superior R y del punto D del engranaje

SOLUCIÓN • Del dibujo se observa que el centro instantáneo C tiene velocidad nula. • Entonces el punto A describe una circunferencia con centro en C. Su velocidad angular será • De igual forma se dice que los puntos de la rueda giran con centro instatnátneo en C

Aceleración absoluta y relativa en movimiento plano Aceleración absoluta de una partícula de la placa, • La aceleración relativa asociada con la rotación alrededor de A incluye las componentes tangencial y normal

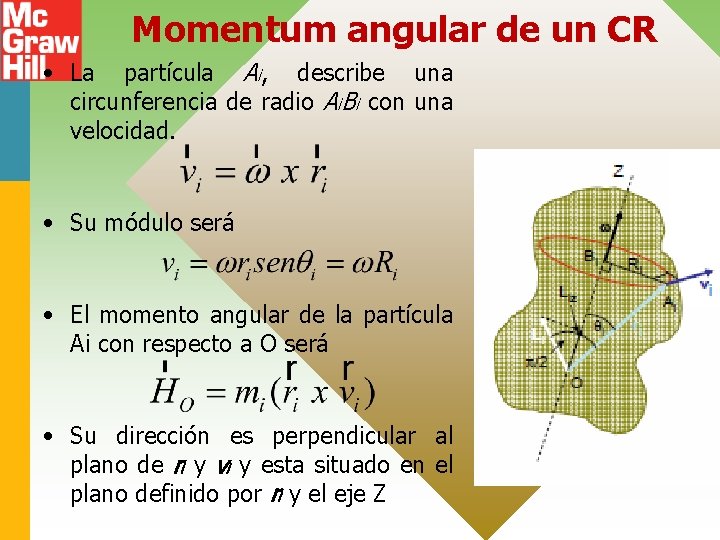
Momentum angular de un CR • La partícula Ai, describe una circunferencia de radio Ai. Bi con una velocidad. • Su módulo será • El momento angular de la partícula Ai con respecto a O será • Su dirección es perpendicular al plano de ri y vi y esta situado en el plano definido por ri y el eje Z

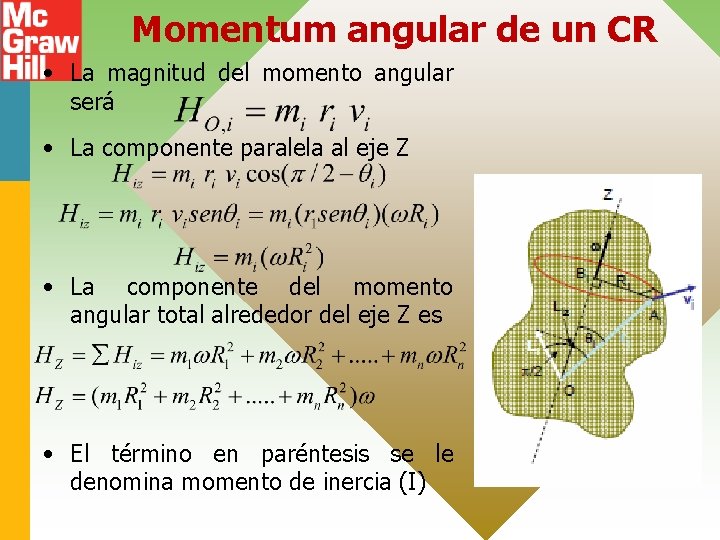
Momentum angular de un CR • La magnitud del momento angular será • La componente paralela al eje Z • La componente del momento angular total alrededor del eje Z es • El término en paréntesis se le denomina momento de inercia (I)

Momentum angular de un CR • El momento de inercia será • El momento angular alrededor del eje z en función del momento inercia • El momento angular total será Este momento no tiene necesarimante que ser paralelo al eje de rotación

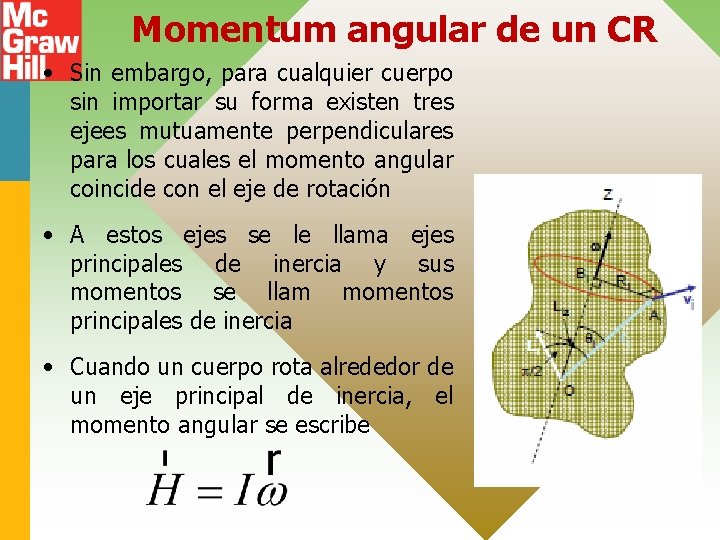
Momentum angular de un CR • Sin embargo, para cualquier cuerpo sin importar su forma existen tres ejees mutuamente perpendiculares para los cuales el momento angular coincide con el eje de rotación • A estos ejes se le llama ejes principales de inercia y sus momentos se llam momentos principales de inercia • Cuando un cuerpo rota alrededor de un eje principal de inercia, el momento angular se escribe

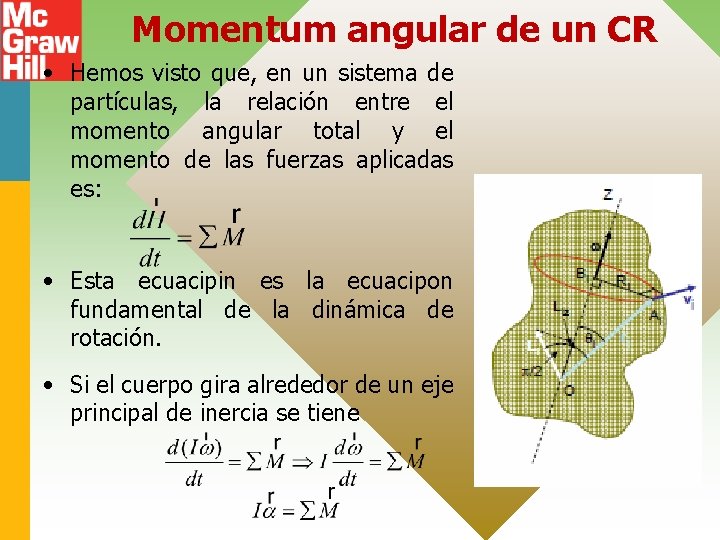
Momentum angular de un CR • Hemos visto que, en un sistema de partículas, la relación entre el momento angular total y el momento de las fuerzas aplicadas es: • Esta ecuacipin es la ecuacipon fundamental de la dinámica de rotación. • Si el cuerpo gira alrededor de un eje principal de inercia se tiene

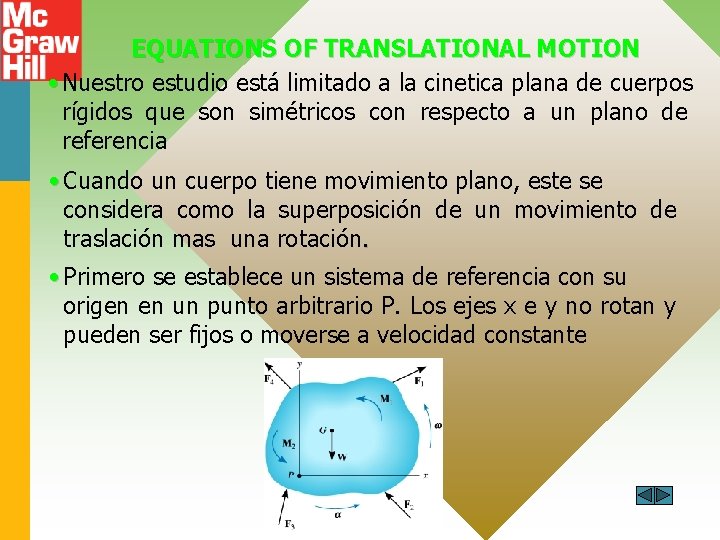
EQUATIONS OF TRANSLATIONAL MOTION • Nuestro estudio está limitado a la cinetica plana de cuerpos rígidos que son simétricos con respecto a un plano de referencia • Cuando un cuerpo tiene movimiento plano, este se considera como la superposición de un movimiento de traslación mas una rotación. • Primero se establece un sistema de referencia con su origen en un punto arbitrario P. Los ejes x e y no rotan y pueden ser fijos o moverse a velocidad constante

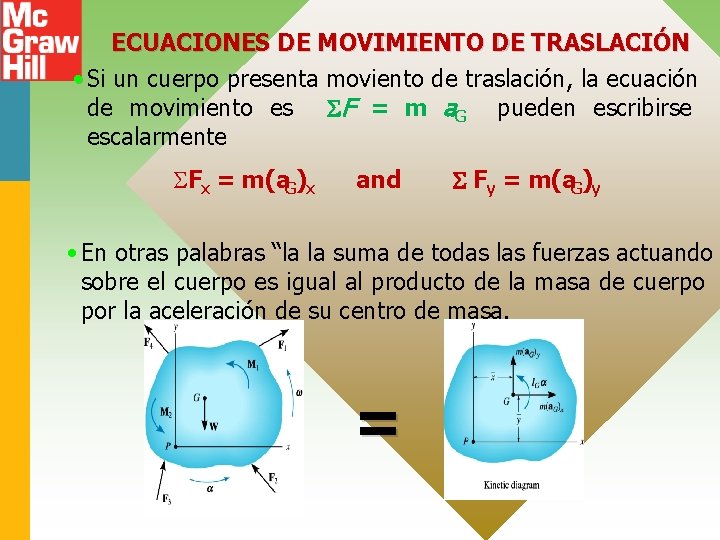
ECUACIONES DE MOVIMIENTO DE TRASLACIÓN • Si un cuerpo presenta moviento de traslación, la ecuación de movimiento es F = m a. G pueden escribirse escalarmente Fx = m(a. G)x and Fy = m(a. G)y • En otras palabras “la la suma de todas las fuerzas actuando sobre el cuerpo es igual al producto de la masa de cuerpo por la aceleración de su centro de masa. =

Ecuaciones de movimiento de rotación Necesitamos determinar el efecto cusado por las fuerzas externas del sistema. El momento respecto a P se escribe ( r i F i ) + M i = r G m a G + IG M p = ( Mk ) p donde Mp es el momento resultante alredeor de P debido a las fuerzas externas y el término (Mk)p se le llama momento cinético alredeor de P =

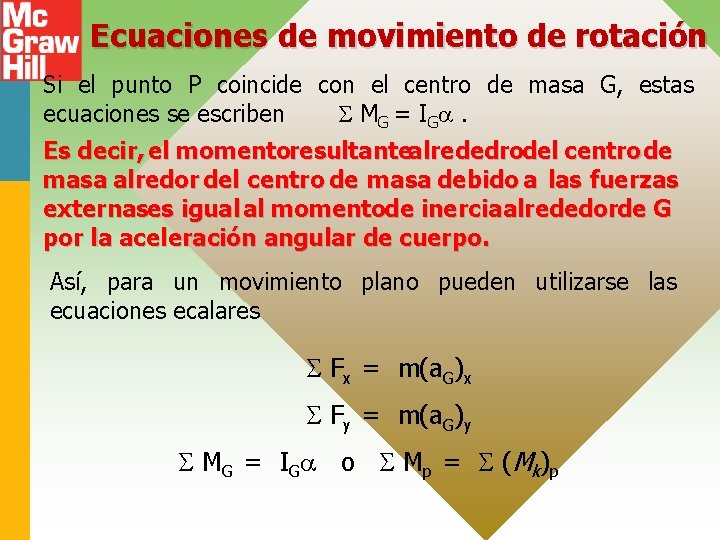
Ecuaciones de movimiento de rotación Si el punto P coincide con el centro de masa G, estas ecuaciones se escriben M G = I G . Es decir, el momentoresultantealrededrodel centro de masa alredor del centro de masa debido a las fuerzas externases igual al momentode inerciaalrededorde G por la aceleración angular de cuerpo. Así, para un movimiento plano pueden utilizarse las ecuaciones ecalares Fx = m(a. G)x Fy = m(a. G)y M G = I G o M p = ( M k) p

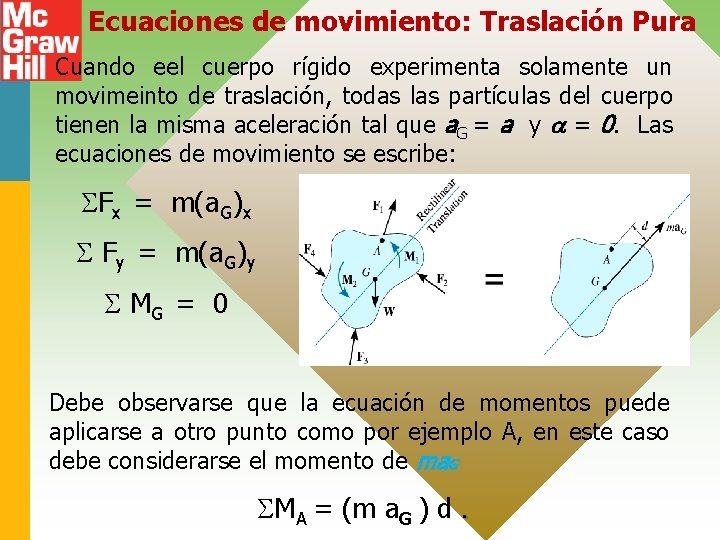
Ecuaciones de movimiento: Traslación Pura Cuando eel cuerpo rígido experimenta solamente un movimeinto de traslación, todas las partículas del cuerpo tienen la misma aceleración tal que a. G = a y = 0. Las ecuaciones de movimiento se escribe: Fx = m(a. G)x Fy = m(a. G)y MG = 0 Debe observarse que la ecuación de momentos puede aplicarse a otro punto como por ejemplo A, en este caso debe considerarse el momento de ma. G MA = (m a. G ) d.

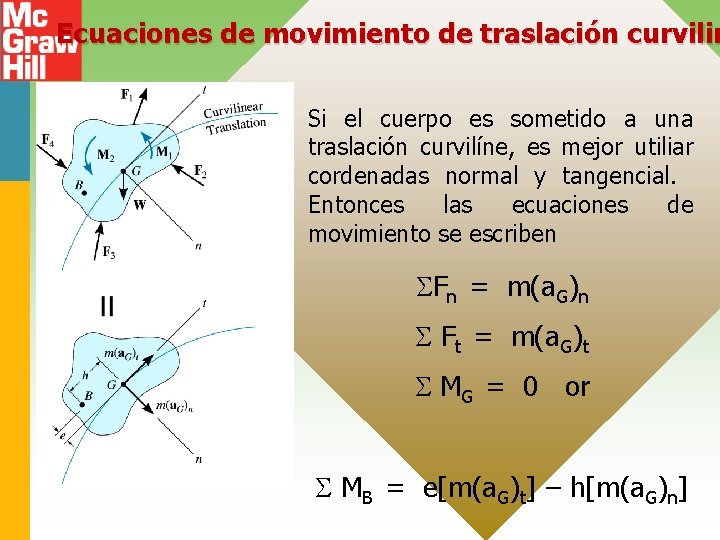
Ecuaciones de movimiento de traslación curvilin Si el cuerpo es sometido a una traslación curvilíne, es mejor utiliar cordenadas normal y tangencial. Entonces las ecuaciones de movimiento se escriben Fn = m(a. G)n Ft = m(a. G)t MG = 0 or MB = e[m(a. G)t] – h[m(a. G)n]

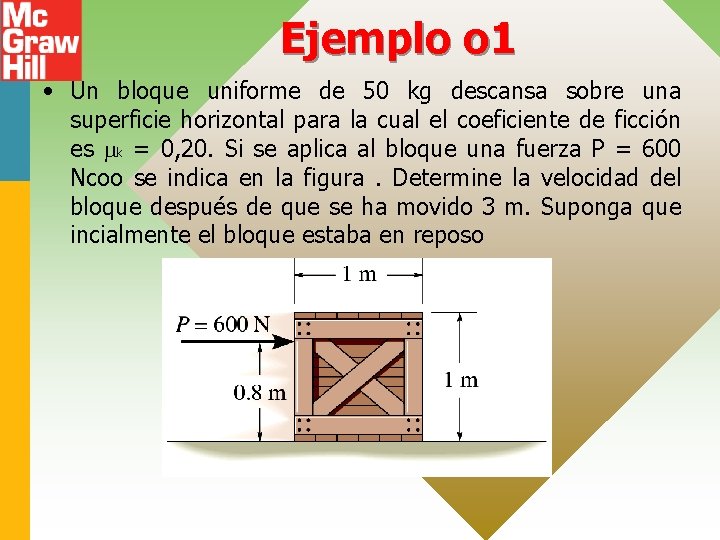
Ejemplo o 1 • Un bloque uniforme de 50 kg descansa sobre una superficie horizontal para la cual el coeficiente de ficción es k = 0, 20. Si se aplica al bloque una fuerza P = 600 Ncoo se indica en la figura. Determine la velocidad del bloque después de que se ha movido 3 m. Suponga que incialmente el bloque estaba en reposo

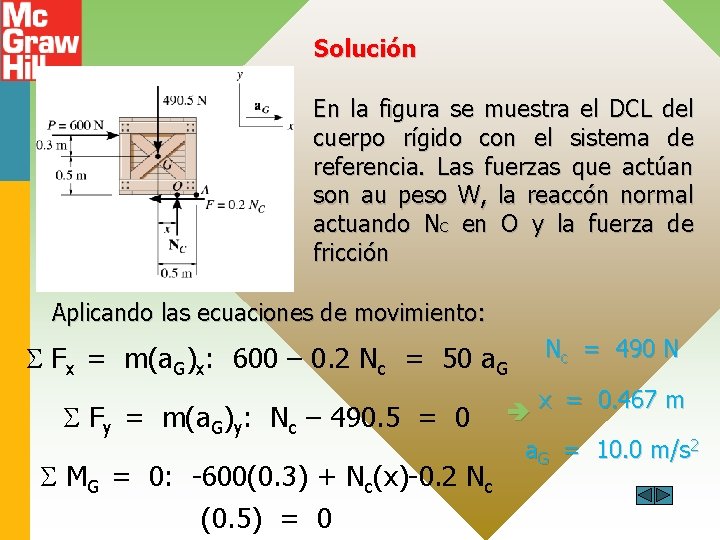
Solución En la figura se muestra el DCL del cuerpo rígido con el sistema de referencia. Las fuerzas que actúan son au peso W, la reaccón normal actuando NC en O y la fuerza de fricción Aplicando las ecuaciones de movimiento: Fx = m(a. G)x: 600 – 0. 2 Nc = 50 a. G Fy = m(a. G)y: Nc – 490. 5 = 0 MG = 0: -600(0. 3) + Nc(x)-0. 2 Nc (0. 5) = 0 Nc = 490 N x = 0. 467 m a. G = 10. 0 m/s 2

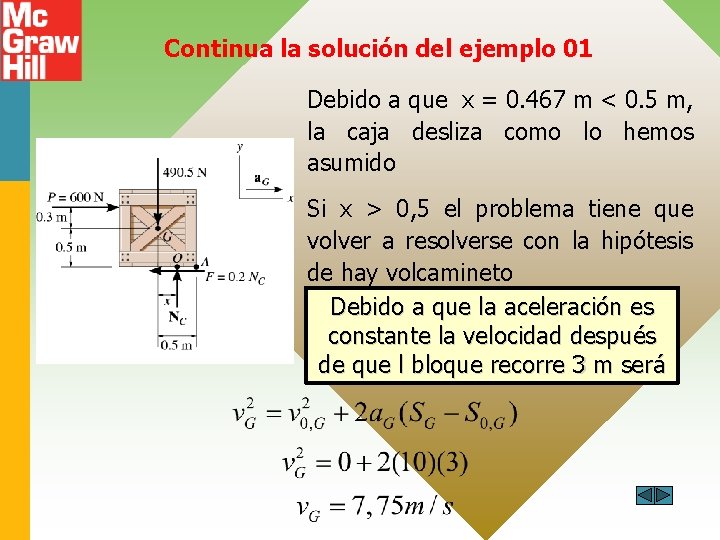
Continua la solución del ejemplo 01 Debido a que x = 0. 467 m < 0. 5 m, la caja desliza como lo hemos asumido Si x > 0, 5 el problema tiene que volver a resolverse con la hipótesis de hay volcamineto Debido a que la aceleración es constante la velocidad después de que l bloque recorre 3 m será

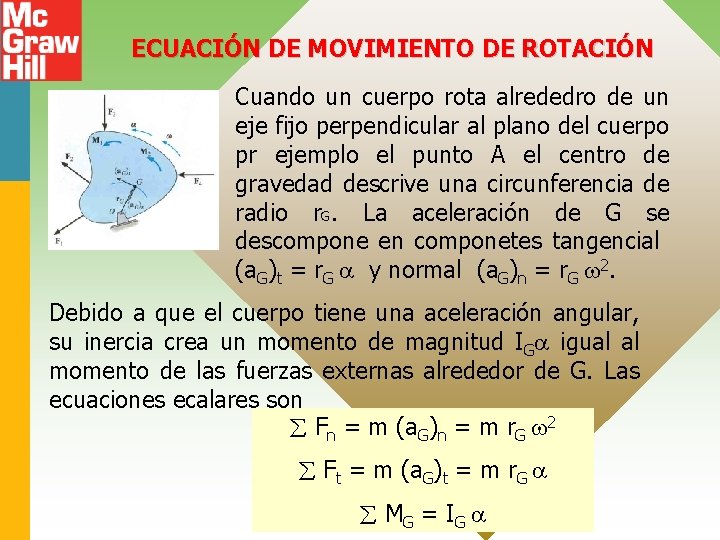
ECUACIÓN DE MOVIMIENTO DE ROTACIÓN Cuando un cuerpo rota alrededro de un eje fijo perpendicular al plano del cuerpo pr ejemplo el punto A el centro de gravedad descrive una circunferencia de radio r. G. La aceleración de G se descompone en componetes tangencial (a. G)t = r. G y normal (a. G)n = r. G 2. Debido a que el cuerpo tiene una aceleración angular, su inercia crea un momento de magnitud IG igual al momento de las fuerzas externas alrededor de G. Las ecuaciones ecalares son Fn = m (a. G)n = m r. G 2 Ft = m (a. G)t = m r. G MG = I G

ECUACIONES DE MOVIMIENTO DE ROTACIÓN ALREDEDOR DE UN EJ FIJO Note que la ecución de momentos MG puede ser rempalzada por una suma de momentos alrededor de un punto arbitrario. MO = IG + r. G m (a. G) t = (IG + m (r. G)2 ) Usando el teorema de los ejes paralelos, el término entre paréntesis es igual al momento d inercia respecto de O, IO = IG + m(r. G)2, . Entonces la ecuaciones escalares se escriben Fn = m (a. G) n = m r. G 2 Ft = m (a. G) t = m r. G MO = IO

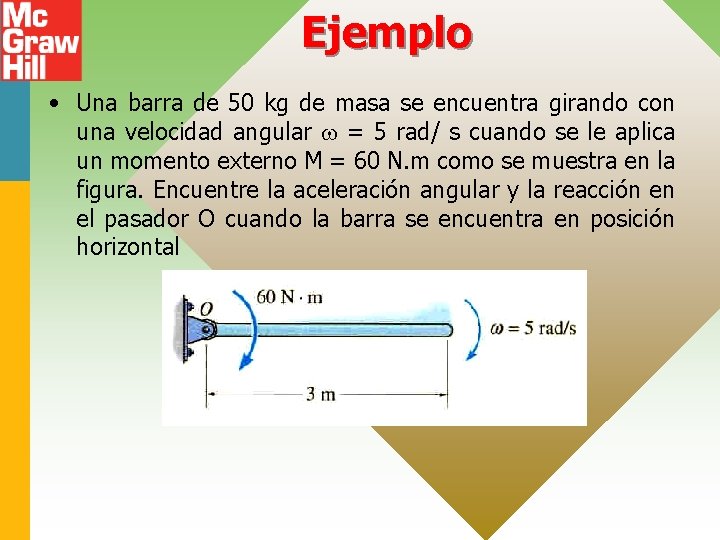
Ejemplo • Una barra de 50 kg de masa se encuentra girando con una velocidad angular = 5 rad/ s cuando se le aplica un momento externo M = 60 N. m como se muestra en la figura. Encuentre la aceleración angular y la reacción en el pasador O cuando la barra se encuentra en posición horizontal

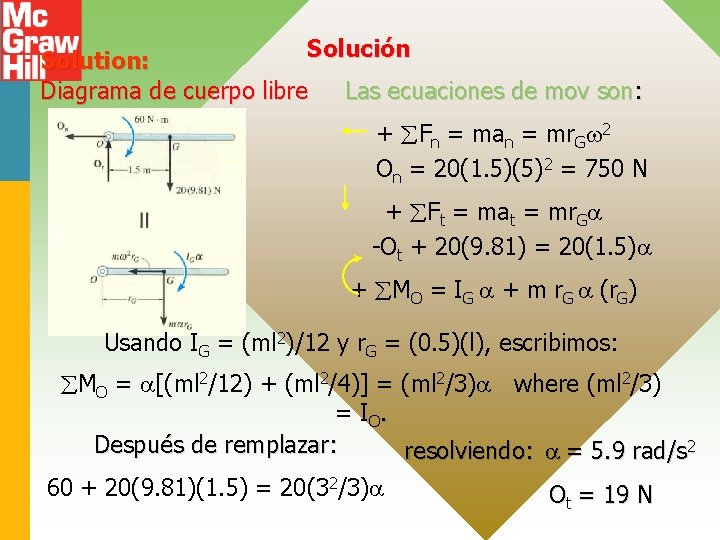
Solución Solution: Diagrama de cuerpo libre Las ecuaciones de mov son: + Fn = man = mr. G 2 On = 20(1. 5)(5)2 = 750 N + Ft = mat = mr. G -Ot + 20(9. 81) = 20(1. 5) + MO = IG + m r. G (r. G) Usando IG = (ml 2)/12 y r. G = (0. 5)(l), escribimos: MO = [(ml 2/12) + (ml 2/4)] = (ml 2/3) where (ml 2/3) = I O. Después de remplazar: resolviendo: = 5. 9 rad/s 2 60 + 20(9. 81)(1. 5) = 20(32/3) Ot = 19 N

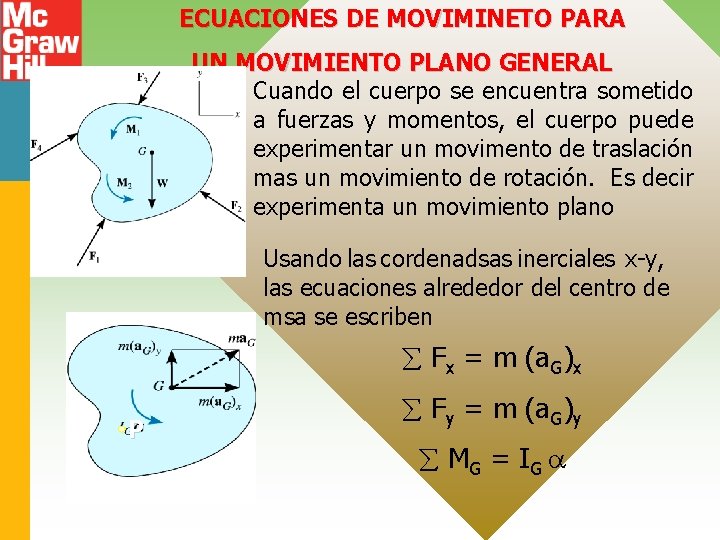
ECUACIONES DE MOVIMINETO PARA UN MOVIMIENTO PLANO GENERAL Cuando el cuerpo se encuentra sometido a fuerzas y momentos, el cuerpo puede experimentar un movimento de traslación mas un movimiento de rotación. Es decir experimenta un movimiento plano Usando las cordenadsas inerciales x-y, las ecuaciones alrededor del centro de msa se escriben Fx = m (a. G)x P Fy = m (a. G)y MG = I G

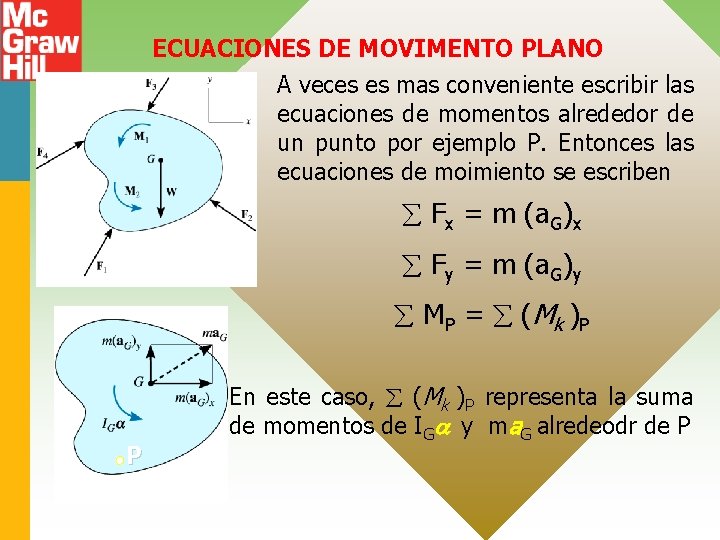
ECUACIONES DE MOVIMENTO PLANO A veces es mas conveniente escribir las ecuaciones de momentos alrededor de un punto por ejemplo P. Entonces las ecuaciones de moimiento se escriben Fx = m (a. G)x Fy = m (a. G)y M P = ( Mk ) P P En este caso, (Mk )P representa la suma de momentos de IG y ma. G alredeodr de P

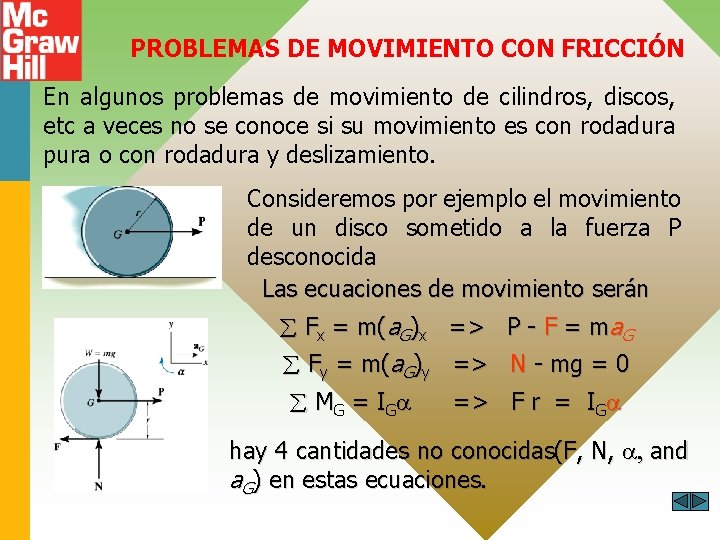
PROBLEMAS DE MOVIMIENTO CON FRICCIÓN En algunos problemas de movimiento de cilindros, discos, etc a veces no se conoce si su movimiento es con rodadura pura o con rodadura y deslizamiento. Consideremos por ejemplo el movimiento de un disco sometido a la fuerza P desconocida Las ecuaciones de movimiento serán Fx = m(a. G)x => P - F = ma. G Fy = m(a. G)y => N - mg = 0 M G = I G => F r = IG hay 4 cantidades no conocidas(F, N, , and a. G) en estas ecuaciones.