UNIVERSIDAD MAYOR DE SAN ANDRS FACULTAD DE CIENCIAS

UNIVERSIDAD MAYOR DE SAN ANDRÉS FACULTAD DE CIENCIAS ECONÓMICAS Y FINANCIERAS CARRERA DE ADMINISTRACIÓN DE EMPRESAS ASIGNATURA: FINANZAS II TEMA Nº 3 TEORÍA DEL VALOR El valor del dinero a través del tiempo WILFREDO MATIAS ® Especialista en Finanzas & Gerencia wilfredo. matias@gmail. com

INVERSIÓN Cualquier sacrificio de recursos hoy con la esperanza de recibir algún beneficio en el futuro.

El Concepto de inversión sacrificio de recursos hoy con la esperanza de recibir algún beneficio en el futuro. • Tendencia al consumo inmediato • Si se quiere que alguien no consuma algo, hay que recompensarla. • Ejemplo: ¿Si Usted tiene el dinero para comprar un carro hoy, guardaría ese dinero debajo del colchón para adquirirlo dentro de un año?

El Concepto de inversión sacrificio de recursos hoy con la esperanza de recibir algún beneficio en el futuro. • No solamente se evalúan los recursos monetarios, también se deben tener en cuenta los demás recursos DESEABLES y ESCASOS. • Un problema: La valoración de los activos.

El Concepto de inversión sacrificio de recursos hoy con la esperanza de recibir algún beneficio en el futuro • El tiempo es el elemento principal de la matemática financiera: • El valor del dinero como recurso tiene sentido UNICAMENTE cuando este se usa por un periodo de tiempo.

El Concepto de inversión sacrificio de recursos hoy con la esperanza de recibir algún beneficio en el futuro • En cualquier inversión, existe el riesgo de no recibir parte o toda la inversión y los beneficios esperados.

El Concepto de inversión sacrificio de recursos hoy con la esperanza de recibir algún beneficio en el futuro • Implica que además de recibir la inversión, debe recibir algún recurso adicional. Beneficio = Recuperación de la inversión + Ingreso Intereses adicional

Estudiando los “Beneficios”. . . La tasa de Interés: La tasa de interés es la utilidad (rentabilidad) medida en términos porcentuales del rendimiento de un capital determinado

Estudiando los “Beneficios”. . . ¿De cuánto deben ser estos beneficios o intereses? ¿Cuánto es lo mínimo que debo cobrar para no perder? Los beneficios deberán cubrir: 1. La pérdida del poder adquisitivo. (Inflación) 2. El riesgo de perder una parte o todo el dinero. 3. El “sacrificio” de no consumir ahora (componente real)

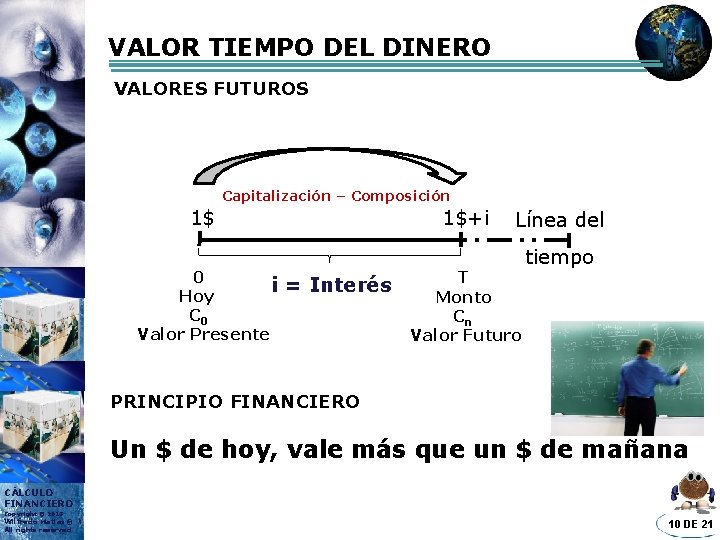
VALOR TIEMPO DEL DINERO VALORES FUTUROS Capitalización – Composición 1$ 0 i Hoy C 0 Valor Presente 1$+i = Interés Línea del T Monto Cn Valor Futuro tiempo PRINCIPIO FINANCIERO Un $ de hoy, vale más que un $ de mañana CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 10 DE 21

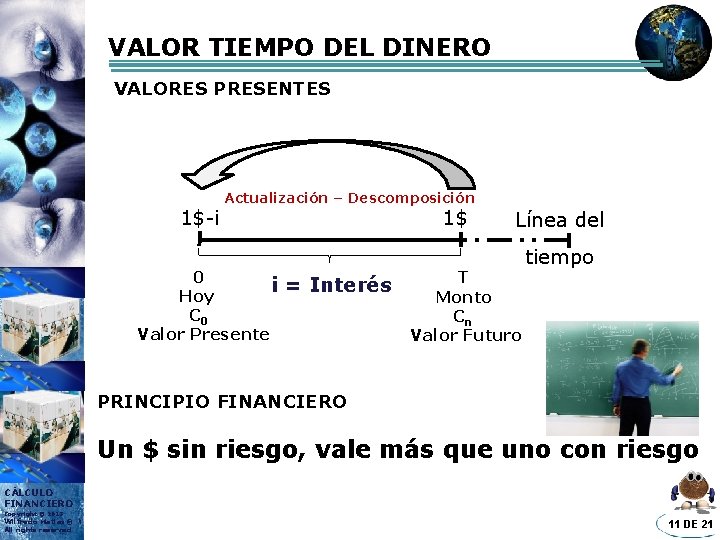
VALOR TIEMPO DEL DINERO VALORES PRESENTES 1$-i Actualización – Descomposición 0 i Hoy C 0 Valor Presente 1$ = Interés Línea del T Monto Cn Valor Futuro tiempo PRINCIPIO FINANCIERO Un $ sin riesgo, vale más que uno con riesgo CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 11 DE 21

OPERACIÓN FINANCIERA Es toda acción que produzca, por desplazamiento en el tiempo una variación cuantitativa del capital. Tal capital está sometido a un régimen financiero, constituyendo su estudio y la valuación de sus efectos cuantitativos, el objetivo del cálculo financiero. VARIABLES: Capital (C 0), Tiempo (T) (duración de la operación), tasa de interés(i), la cual genera el rendimiento de la operación: El interés es el precio del uso del capital en un determinado tiempo. CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 12 DE 21

RÉGIMEN SIMPLE Los intereses siempre son calculados, sobre un capital inicial, por lo cual es posible aseverar que los intereses ganados no generan nuevos intereses. Lo anterior permite deducir que los intereses representan una suma fija. El interés que produce un capital es proporcional a: Dicho capital (monto – importe) El tiempo por el cual está colocado, y la tasa (%) de interés. CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 13 DE 21

RÉGIMEN SIMPLE FÓRMULAS DERIVADAS VALOR ACTUAL TIEMPO TASA DE INTERÉS ACUMULADO CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 14 DE 21

INTERÉS COMPUESTO CÁLCULO FINANCIERO Al hablar de interés compuesto se hace mención al régimen en el que se produce la capitalización de intereses , lo cual implica, que los intereses producidos en un periodo se incorpora al capital, para producir nuevos intereses. Si un capital C 0 al terminar un periodo de inversión (por ejemplo un año) genera un INTERÉS; (el cual se integra el capital inicial C 0), dicho valor no se retira entonces al segundo periodo éste dinero empieza a crecer nuevamente como si fuera un nuevo capital. Proceso conocido como capitalización. Copyright © 2013 Wilfredo Matias® All rights reserved 15 DE 21

INTERÉS COMPUESTO En el interés compuesto el valor del dinero generado por concepto de intereses, se convierte parte del capital en el siguiente periodode capitalización. Para que se de la capitalización, debe existir más de un período. CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved Los intereses producidos al término de cada período de capitalización se acumulan al capital que los generó es decir “se capitalizan”. El capital tiene un crecimiento que es proporcional a su valor durante el período anterior. Período de capitalización (m): número de veces en el periodo, en que los intereses se adicionan al capital. 16 DE 21

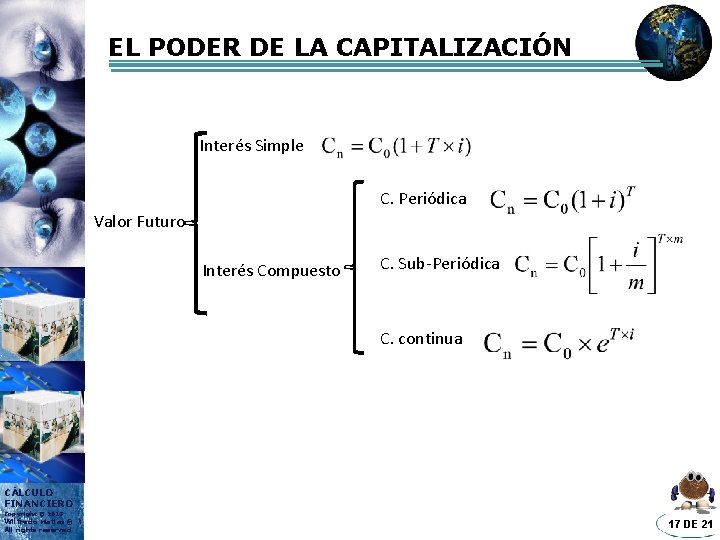
EL PODER DE LA CAPITALIZACIÓN Interés Simple C. Periódica Valor Futuro Interés Compuesto C. Sub-Periódica C. continua CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 17 DE 21

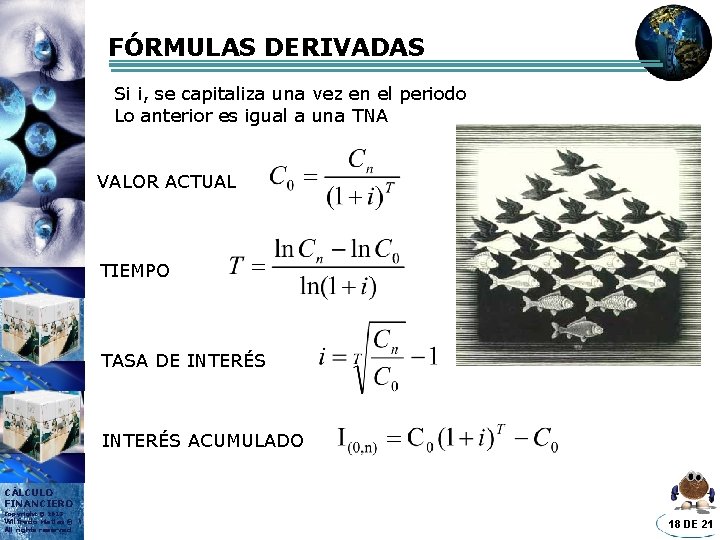
FÓRMULAS DERIVADAS Si i, se capitaliza una vez en el periodo Lo anterior es igual a una TNA VALOR ACTUAL TIEMPO TASA DE INTERÉS ACUMULADO CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 18 DE 21

TASA NOMINAL, EFECTIVA, EQ. Y REAL TNA A TEA A TNA TEA A TEq TNA CONTINUO A TEA TASA REAL CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 19 DE 21

En resumen. . Tres tipos de tasas: • Nominal: Nominal Es una tasa pactada para un período, pero los rendimientos (intereses) se pagan en períodos menores al pactado en la tasa. 24. 63% capitalizable mes • Efectiva: Efectiva Es una tasa a la cual se llega capitalizando los intereses pagados antes de que se culmine el período pactado para la tasa nominal. 27, 61% efectivo año • Periódica: Periódica Es la tasa pactada para un periodo. Con ella se calculan los flujos de caja. 6, 28% Trimestral. CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 20 DE 21

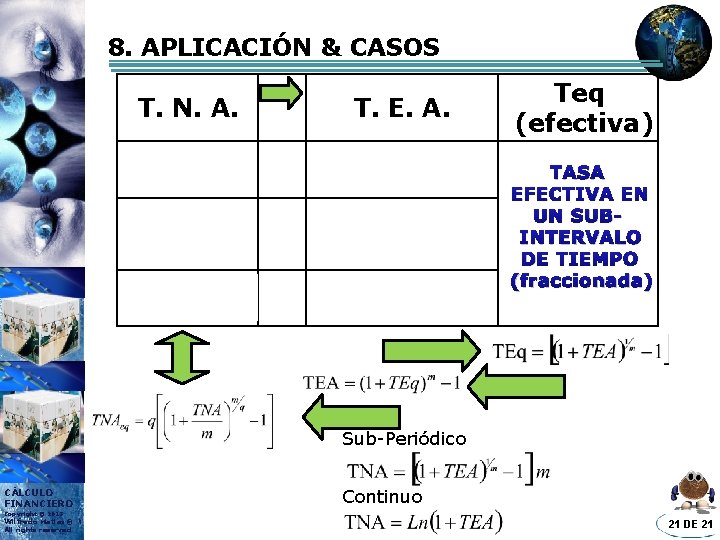
8. APLICACIÓN & CASOS T. N. A. T. E. A. TNA PERIÓDICO = TNA SUBPERIÓDICO < TNA CONTINUO < TEA Teq (efectiva) TASA EFECTIVA EN UN SUBINTERVALO DE TIEMPO (fraccionada) Sub-Periódico CÁLCULO FINANCIERO Continuo Copyright © 2013 Wilfredo Matias® All rights reserved 21 DE 21

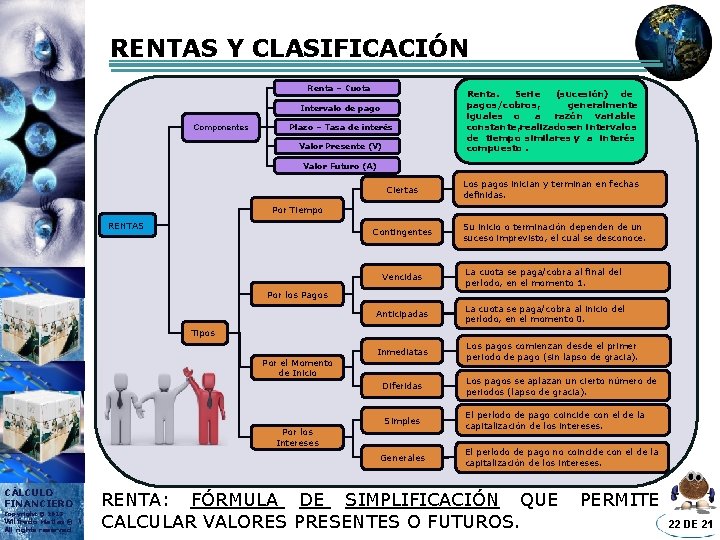
RENTAS Y CLASIFICACIÓN Renta – Cuota Intervalo de pago Componentes Plazo – Tasa de interés Valor Presente (V) Renta. Serie (sucesión) de pagos/cobros, generalmente iguales o a razón variable constante, realizadosen intervalos de tiempo similares y a interés compuesto. Valor Futuro (A) Ciertas Los pagos inician y terminan en fechas definidas. Por Tiempo RENTAS Contingentes Su inicio o terminación dependen de un suceso imprevisto, el cual se desconoce. Vencidas La cuota se paga/cobra al final del período, en el momento 1. Anticipadas La cuota se paga/cobra al inicio del período, en el momento 0. Inmediatas Los pagos comienzan desde el primer periodo de pago (sin lapso de gracia). Por los Pagos Tipos Por el Momento de Inicio Diferidas Los pagos se aplazan un cierto número de periodos (lapso de gracia). Simples El período de pago coincide con el de la capitalización de los intereses. Por los Intereses Generales CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved El período de pago no coincide con el de la capitalización de los intereses. RENTA: FÓRMULA DE SIMPLIFICACIÓN QUE CALCULAR VALORES PRESENTES O FUTUROS. PERMITE 22 DE 21

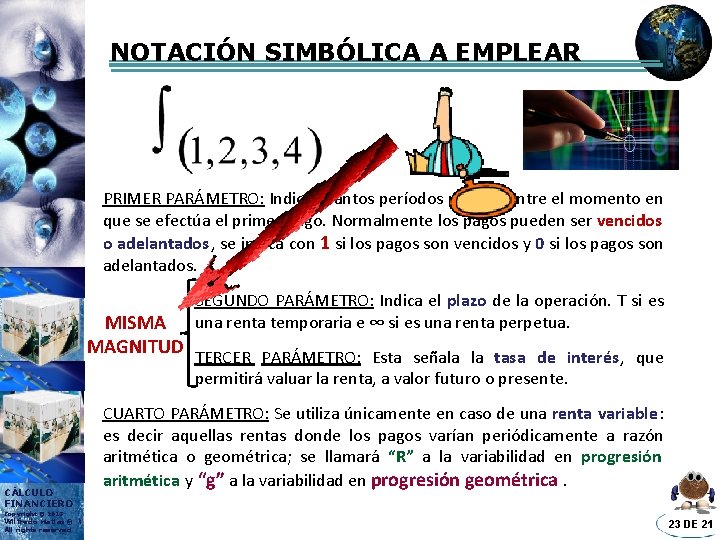
NOTACIÓN SIMBÓLICA A EMPLEAR PRIMER PARÁMETRO: Indica cuántos períodos median entre el momento en que se efectúa el primer pago. Normalmente los pagos pueden ser vencidos o adelantados, se indica con 1 si los pagos son vencidos y 0 si los pagos son adelantados. SEGUNDO PARÁMETRO: Indica el plazo de la operación. T si es una renta temporaria e ∞ si es una renta perpetua. MISMA MAGNITUD TERCER PARÁMETRO: Esta señala la tasa de interés, que permitirá valuar la renta, a valor futuro o presente. CÁLCULO FINANCIERO CUARTO PARÁMETRO: Se utiliza únicamente en caso de una renta variable: es decir aquellas rentas donde los pagos varían periódicamente a razón aritmética o geométrica; se llamará “R” a la variabilidad en progresión aritmética y “g” a la variabilidad en progresión geométrica. Copyright © 2013 Wilfredo Matias® All rights reserved 23 DE 21

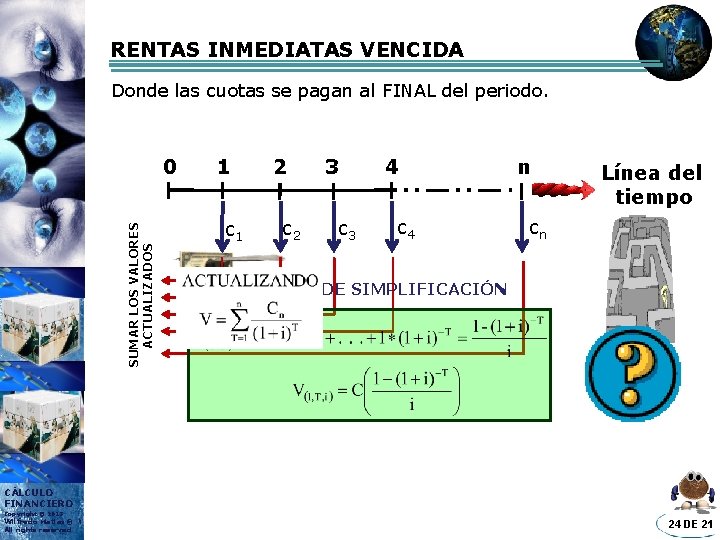
RENTAS INMEDIATAS VENCIDA Donde las cuotas se pagan al FINAL del periodo. SUMAR LOS VALORES ACTUALIZADOS 0 1 c 1 2 c 2 3 c 3 4 c 4 n Línea del tiempo cn FÓRMULA DE SIMPLIFICACIÓN CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 24 DE 21

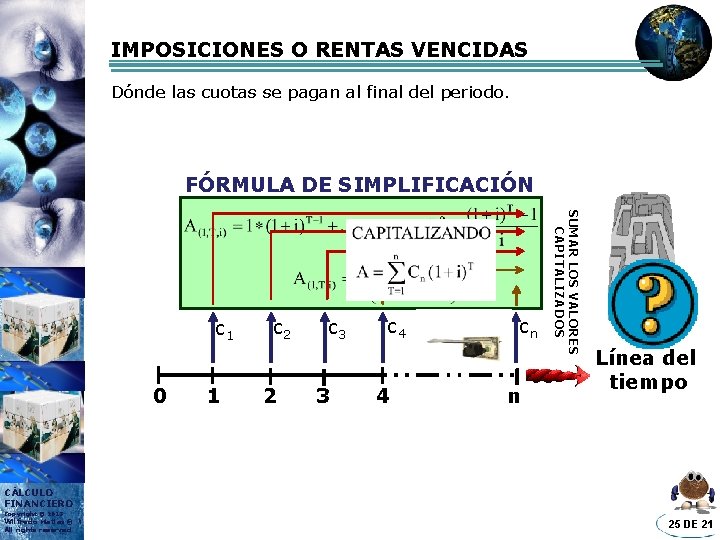
IMPOSICIONES O RENTAS VENCIDAS Dónde las cuotas se pagan al final del periodo. FÓRMULA DE SIMPLIFICACIÓN 0 1 c 2 2 c 3 3 c 4 4 cn n SUMAR LOS VALORES CAPITALIZADOS c 1 Línea del tiempo CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 25 DE 21

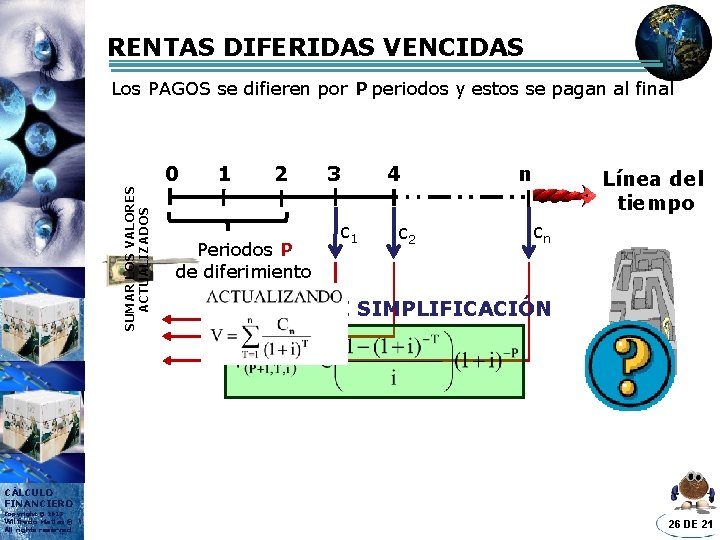
RENTAS DIFERIDAS VENCIDAS Los PAGOS se difieren por P periodos y estos se pagan al final SUMAR LOS VALORES ACTUALIZADOS 0 1 2 Periodos P de diferimiento 3 c 1 4 c 2 n Línea del tiempo cn FÓRMULA DE SIMPLIFICACIÓN CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 26 DE 21

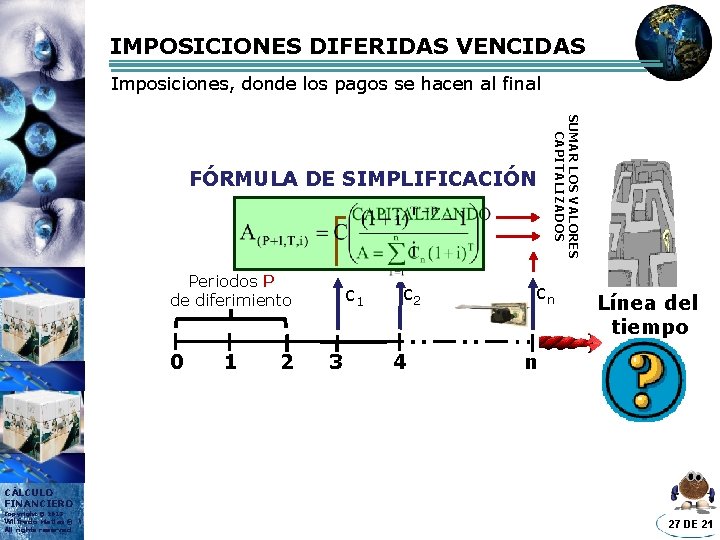
IMPOSICIONES DIFERIDAS VENCIDAS Imposiciones, donde los pagos se hacen al final Periodos P de diferimiento 0 1 2 c 1 3 c 2 4 SUMAR LOS VALORES CAPITALIZADOS FÓRMULA DE SIMPLIFICACIÓN cn Línea del tiempo n CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 27 DE 21

GRADIENTES GEOMÉTRICOS DE PAGOS VENCIDOS 0 1 SUMAR LOS VALORES ACTUALIZADOS c 1 2 3 4 n Línea del tiempo C 1(1+g)2 C 1(1+g)3 FÓRMULA DE SIMPLIFICACIÓN C 1(1+g)n-1 CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 28 DE 21

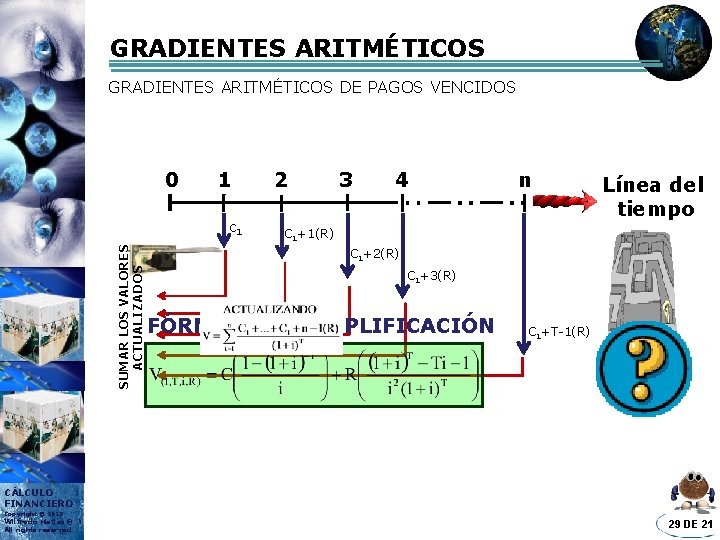
GRADIENTES ARITMÉTICOS DE PAGOS VENCIDOS 0 1 SUMAR LOS VALORES ACTUALIZADOS c 1 2 3 4 n Línea del tiempo C 1+1(R) C 1+2(R) C 1+3(R) FÓRMULA DE SIMPLIFICACIÓN C 1+T-1(R) CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved 29 DE 21

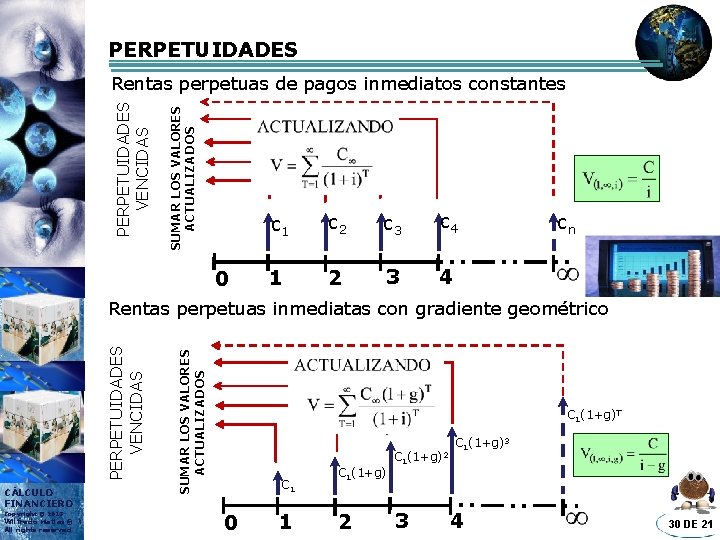
PERPETUIDADES SUMAR LOS VALORES ACTUALIZADOS PERPETUIDADES VENCIDAS Rentas perpetuas de pagos inmediatos constantes 0 c 1 c 2 c 3 c 4 1 2 3 4 cn CÁLCULO FINANCIERO Copyright © 2013 Wilfredo Matias® All rights reserved SUMAR LOS VALORES ACTUALIZADOS PERPETUIDADES VENCIDAS Rentas perpetuas inmediatas con gradiente geométrico C 1(1+g)T C 1 0 1 C 1(1+g) 2 C 1(1+g)2 3 C 1(1+g)3 4 30 DE 21

UNIVERSIDAD MAYOR DE SAN ANDRÉS FACULTAD DE CIENCIAS ECONÓMICAS Y FINANCIERAS CARRERA DE ADMINISTRACIÓN DE EMPRESAS ASIGNATURA: FINANZAS II WILFREDO MATIAS ® Especialista en Finanzas & Gerencia wilfredo. matias@gmail. com