UNIVERSIDAD AUTNOMA METROPOLITANA Unidad Iztapalapa MODELOS MATEMTICOS EN

UNIVERSIDAD AUTÓNOMA METROPOLITANA Unidad Iztapalapa MODELOS MATEMÁTICOS EN BIOLOGÍA Modelos determinísticos & Modelos estocásticos Presentan Cortés Estrada Andrés López Valdez Mariela Lizbeth Martínez Ramos Marisol Munguia Soto Esteban Omar Osnaya Becerril Janet Elizabeth Ramírez Barrios Pedro Santiago Dr. Miguel Ángel Armella Villalpando Trimestre 14 -O 5 de Octubre 2014

Los Modelos matemáticos desarrollados para simular fenómenos que ocurren en la naturaleza Clasificación: * Atendiendo a su naturaleza. * Atendiendo a la unidad poblacional de estudio. * Teniendo en cuenta el tipo de herramientas matemáticas utilizadas.

De acuerdo a su naturaleza los modelos matemáticos pueden ser: Deterministas Estocásticos Cuando las condiciones iniciales del sistema marcan de manera unívoca su comportamiento, no se ven afectados por variaciones aleatorias. La evolución del sistema a simular no es siempre la misma -aún partiendo de las mismas condiciones iniciales-, el modelo se denomina estocástico.

Considerando las herramientas matemáticas utilizadas en el diseño del algoritmo matemático, se puede hacer una clasificación de los modelos matemáticos en: � Continuos: son aquellos en los que las variables involucradas en el mismo pueden tomar infinitos valores dentro de un rango previamente establecido. � Discretos: donde las variables que intervienen en el modelo sólo pueden tomar un número finito de valores. � Mixtos: aquellos en los que algunas variables son continuas y otras discretas.

Modelos deterministas de crecimiento El objetivo de estos modelos es proporcionar una descripción cuantitativa de los fenómenos como el crecimiento. � Crecimiento exponencial en tiempo discreto: Cuando la reproducción es estacional, como en las plantas anuales o en animales con celo, la descripción continua es irreal y una descripción en tiempo discreto, a la manera de un mapeo, es más adecuada. � Crecimiento limitado: El mecanismo de limitación que actúa cuando los individuos de la población deben competir por recursos limitados. La competencia puede ser directa o indirecta, mediada por ejemplo por la propia escasez de los recursos.

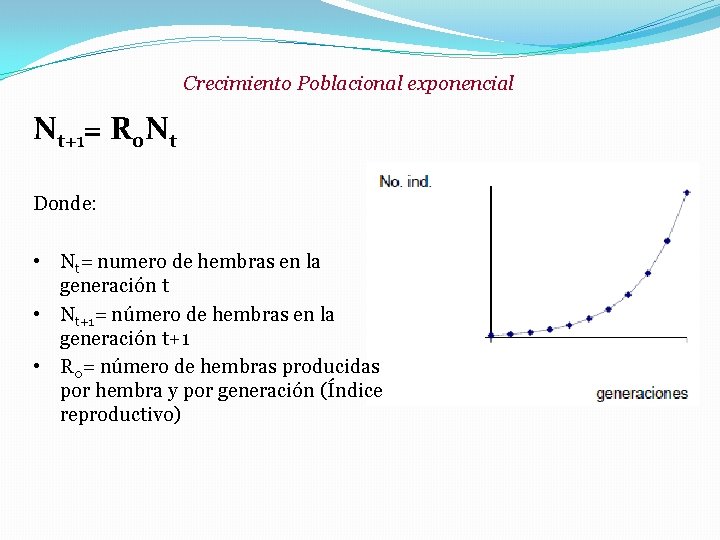
Crecimiento Poblacional exponencial Nt+1= R 0 Nt Donde: • Nt= numero de hembras en la generación t • Nt+1= número de hembras en la generación t+1 • R 0= número de hembras producidas por hembra y por generación (Índice reproductivo)

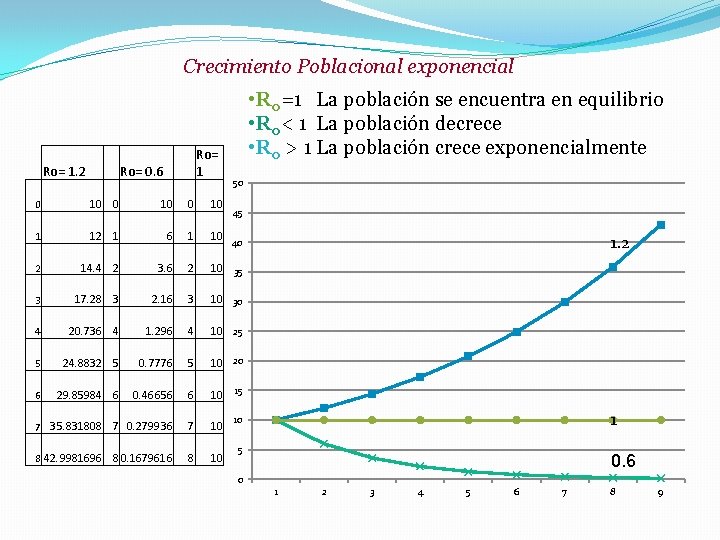
Crecimiento Poblacional exponencial Ro= 1. 2 Ro= 1 Ro= 0. 6 • R 0=1 La población se encuentra en equilibrio • R 0< 1 La población decrece • R 0 > 1 La población crece exponencialmente 50 0 10 1 12 1 6 1 10 40 2 14. 4 2 3. 6 2 10 35 3 17. 28 3 2. 16 3 10 30 4 20. 736 4 1. 296 4 10 25 5 24. 8832 5 0. 7776 5 10 20 6 29. 85984 6 0. 46656 6 10 15 7 35. 831808 7 0. 279936 7 10 8 42. 9981696 8 0. 1679616 8 10 45 1. 2 1 10 5 0. 6 0 1 2 3 4 5 6 7 8 9

Crecimiento Poblacional exponencial Supuestos • El tiempo avanza a pasos discretos • Los recursos del medio son ilimitados • El índice reproductivo neto es constante a lo largo del ciclo de los organismos. (Krebs, 1986)

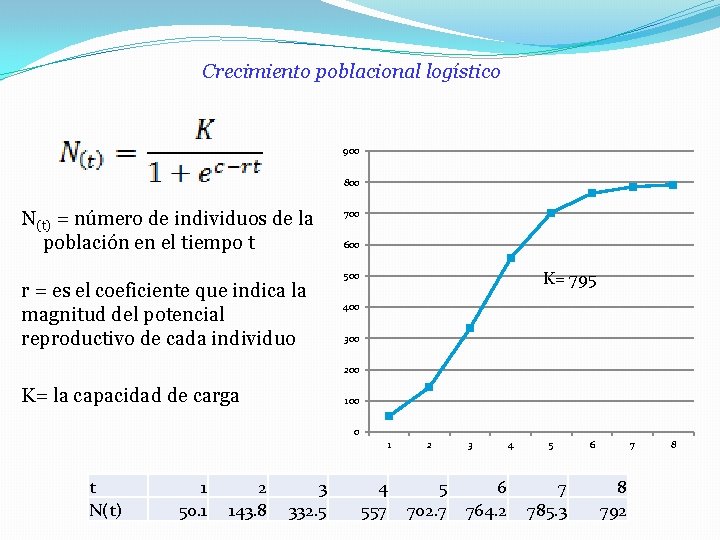
Crecimiento poblacional logístico 900 800 N(t) = número de individuos de la población en el tiempo t r = es el coeficiente que indica la magnitud del potencial reproductivo de cada individuo 700 600 K= 795 500 400 300 200 K= la capacidad de carga 100 0 1 t N(t) 1 50. 1 2 143. 8 3 332. 5 4 557 2 5 702. 7 3 6 764. 2 4 5 7 785. 3 6 7 8 792 8

Crecimiento poblacional logístico Supuestos � Los recursos son limitados � La población tiene una distribución de edades estable. No presenta ningún tipo de inmigración � La respuesta al incremento en la densidad poblacional es instantánea � Las condiciones ambientales son constantes � El incremento en la densidad afecta igualmente a todos los individuos en cualquier grupo de edad � La probabilidad de apareamiento de animales que presentan reproducción sexual no depende de la densidad de población.

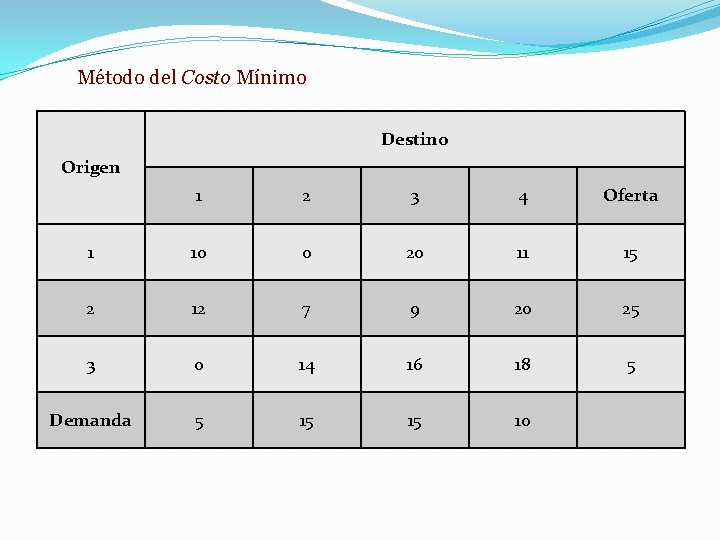
Método del Costo Mínimo � Resolver problemas de transporte o distribución. � Rutas que presentan menores costos. � Asignación de la mayor cantidad de unidades posibles (sujeta a las restricciones de oferta y/o demanda) a la celda menos costosa de toda la matriz hasta finalizar el método.

Método del Costo Mínimo Destino Origen 1 2 3 4 Oferta 1 10 0 20 11 15 2 12 7 9 20 25 3 0 14 16 18 5 Demanda 5 15 15 10

MODELOS ESTOCÁSTICOS ¿Qué es un modelo estocástico? Un modelo es estocástico cuando al menos una variable del mismo es tomada como un dato al azar y las relaciones entre variables se toman por medio de funciones probabilísticas. Los modelos estocásticos, en los que el sistema a una entrada puede tener un conjunto de valores Yi regidos por cierta probabilidad P(Yi) de ocurrencia:

En general, los modelos estocásticos son mas reales que los modelos determinísticos, debido a que los sistemas biológicos rara vez responden con una única salida o respuesta. Del conjunto de posibles valores de respuesta Yi el sistema responde de acuerdo con diversos factores estocásticos del ambiente, P(Yi) así como al encadenamiento de causas y coyunturas aleatorias (Chiappa-Carrera y Sanvicente-Añorve, 1998).

Origen: A partir del modelo logístico, Bartlett (1960) desarrollo el modelo estocástico de crecimiento poblacional. Los supuestos: 1. Se toma en cuenta el efecto aleatorio en los eventos nacimiento y muerte. 2. Se considera por separado el efecto de la densidad poblacional sobre las tasas de natalidad y mortalidad.

Si una población tiene N individuos, dos posibles eventos pueden suceder: un nacimiento o un deceso. Tanto las tasas de natalidad (λ) como la las de mortalidad (μ) están en función del tamaño de la población, y ambas determinan la tasa intrínseca de crecimiento (r) del modelo logístico. Supuestos:

Entonces cada evento (nacimiento o muerte) que se produce en este modelo, tiene cierta probabilidad de ocurrir, factor que modifica enormemente los patrones de crecimiento poblacional.

Modelo estocástico para determinar la mejor estrategia de cuarentena en granjas ganaderas Se parte de que se tiene un total de N granjas, de las cuales S son susceptibles (en riesgo de contraer la enfermedad), E son latentes (infectadas pero todavía no infecciosas), I son infectadas (capaces de transmitir la enfermedad), R son las removidas (aquéllas que han sido eliminadas por el sacrificio y muerte natural de los animales) y Q son las cuarentenadas (aquéllas que han sido aisladas).

Por lo tanto, las probabilidades de transición en este modelo se aproximan a un proceso de Poisson. La densidad conjunta del proceso estocástico es: Pk, l, m, n(t)=P(E(t)=k, I(t)=l, R(t)=m, Q(t)=n) donde: k, l, m, n= 0, 1, 2, 3, …, N y 0≤k+l+m+n ≤N y las tasas de transición instantáneas están dadas por: Pk, l, m, n, k+1, l, m, n(t, t+δ)=λl(N-k-, l-m-n)δ/N+o(δ), Pk, l, m, n, k, l, m, n+1(t, t+δ)=γ(N-k-, l-m-n)/(N-1 -mn))δ+o(δ), Pk, l, m, n; k-1, l+1, m, n(t, t+δ)=µkδ+o(δ), Pk, l, m, n; k-1, l, m+1, n(t, t+δ)=γ(k/(N-l-m-n))δ+o(δ), Pk, l, m, n; k, l-1, m+1, n(t, t+δ)=αlδ+o(δ). . . . (Ec. 1)

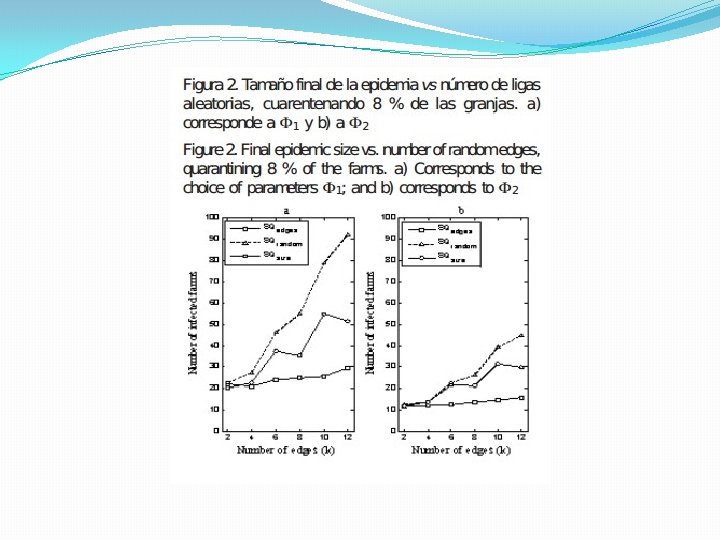
Para estudiar el efecto sobre el tamaño final de la epidemia, se proponen las siguientes tres estrategias de cuarentenas: (SQ): SQedges consiste en cuarentenar a las granjas susceptibles y latentes con el mayornúmero de ligas. SQramdom consiste en cuarentenar a las granjas en forma aleatoria SQsize consiste en cuarentenar a las granjas de mayor tamaño, es decir a las que tienen el mayor número de animales

Cadena de Márkov �Proceso estocástico discreto. �La probabilidad de que ocurra un evento depende solamente del evento inmediatamente anterior. �Si se conoce la historia del sistema hasta su instante actual, su estado presente resume toda la información relevante para describir en probabilidad su estado futuro.

Cadena de Márkov �Se quiere conocer el estado del tiempo en una localidad de estudio. �Se tienen dos condiciones: seco y lluvioso. �Probabilidad de que el día siguiente sea seco es de 0. 8 si el día actual es seco. �Si es lluvioso, la probabilidad de que el día siguiente sea seco es de 0. 6.

Cadena de Márkov Paso 1. Definir variable Paso 2. Matriz de transición. � 0 0 1 1

Cadena de Márkov � Paso 3. Diagrama de transición.

Cadena de Márkov Paso 4. Las probabilidades de estado estable del sistema. � �

Cadena de Márkov

Bibliografía Chiappa–Carrara, X. y L. Sanvicente–Añorve, 1998, El papel de los modelos en el proceso de la investigación. Tópicos de Investigación y Posgrado, 5(4): 204– 211. Chiappa-Carrara, X, M. del C. Galindo de Santiago y A. Cervantes Sandoval. 2009. Introducción a los modelos matemáticos de crecimiento con aplicaciones en sistemas biológicos. UMDI-Sisal, Facultad de Ciencias Facultad de Estudios Superiores Zaragoza. Pag. 93. Krebs, C. J. 1978. Ecology. The Experimental Analysis of Distribution and Abundance. Second Edition. Harper and Row, New York. 678 pp. Montesinos L. A. , C. Hernández S. y A. S. Luna E. 2009. Modelo estocástico para determinar la mejor estrategia de cuarentena en granjas ganaderas. Técnica Pecuaria en México. 47(3): 271 -284