Universality in quantum chaos and the one parameter

Universality in quantum chaos and the one parameter scaling theory Antonio M. García-García ag 3@princeton. edu Princeton University ICTP, Trieste In the semiclassical limit the spectral properties of classically chaotic Hamiltonian are universally described by random matrix theory. With the help of the one parameter scaling theory we propose an alternative characterization of this universality class. It is also identified the universality class associated to the metal-insulator transition. In low dimensions it is characterized by classical superdiffusion. In higher dimensions it has in general a quantum origin as in the case of disordered systems. Systems in this universality class include: kicked rotors with certain classical singularities, polygonal and Coulomb billiards and the Harper model. In collaboration with Wang Jiao PRL 94, 244102 (2005), PRE 2007 in press

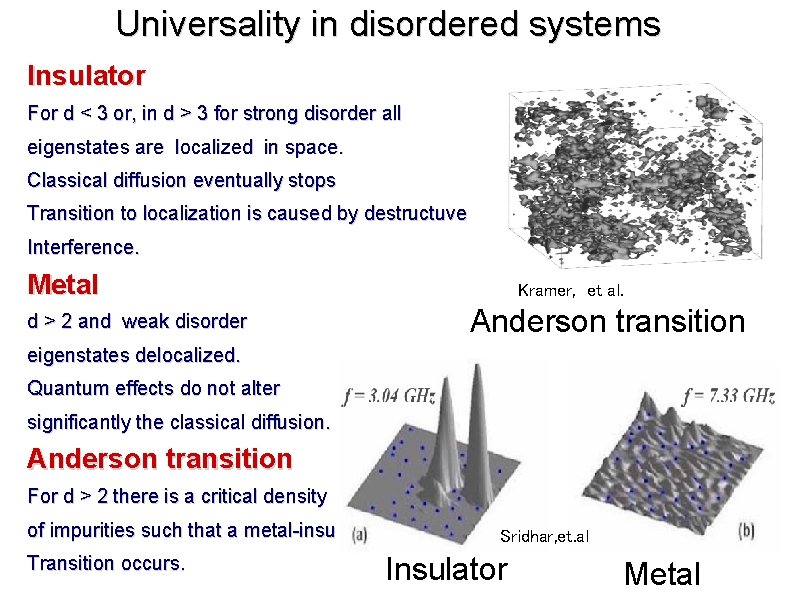
Universality in disordered systems Insulator For d < 3 or, in d > 3 for strong disorder all eigenstates are localized in space. Classical diffusion eventually stops Transition to localization is caused by destructuve Interference. Metal d > 2 and weak disorder Kramer, et al. Anderson transition eigenstates delocalized. Quantum effects do not alter significantly the classical diffusion. Anderson transition For d > 2 there is a critical density of impurities such that a metal-insulator Transition occurs. Sridhar, et. al Insulator Metal

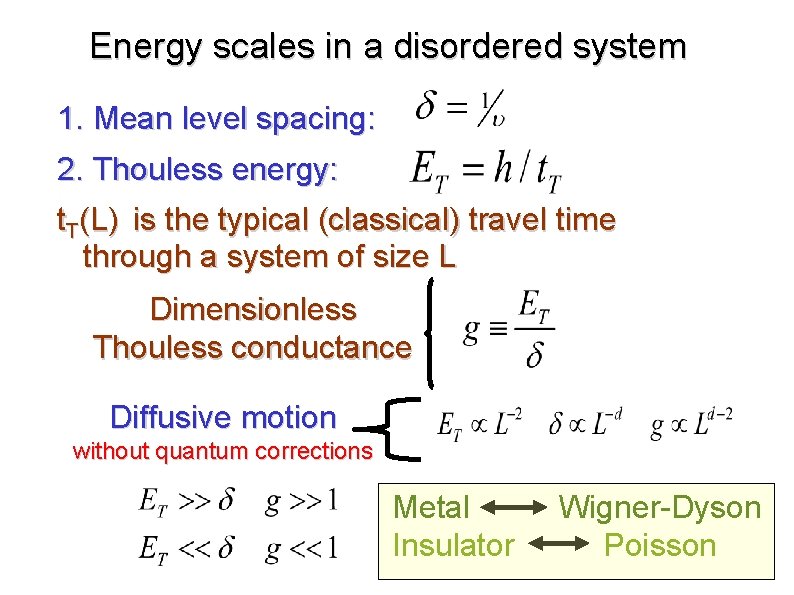
Energy scales in a disordered system 1. Mean level spacing: 2. Thouless energy: t. T(L) is the typical (classical) travel time through a system of size L Dimensionless Thouless conductance Diffusive motion without quantum corrections Metal Insulator Wigner-Dyson Poisson

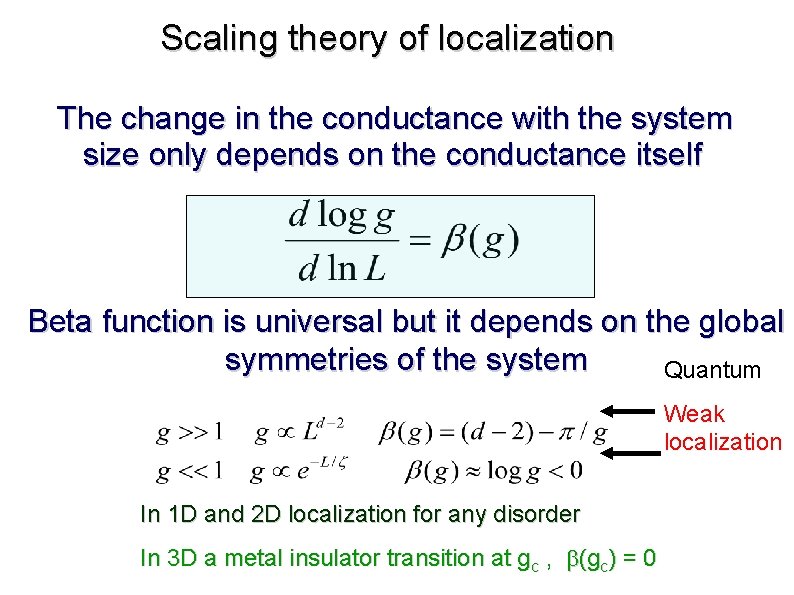
Scaling theory of localization The change in the conductance with the system size only depends on the conductance itself Beta function is universal but it depends on the global symmetries of the system Quantum Weak localization In 1 D and 2 D localization for any disorder In 3 D a metal insulator transition at gc , (gc) = 0

Altshuler, Introduction to mesoscopic physics

Scaling theory and anomalous diffusion de is related to the fractal dimension of the spectrum. The average is over initial conditions and/or ensemble Lapidus, fractal billiards Universality Wigner-Dyson Poisson (g) > 0 (g) < 0 weak localization? Two routes to the Anderson transition 1. Semiclassical origin 2. Induced by quantum effects

How to apply this to quantum chaos? 1. Only for classical systems with an homogeneous phase space. Not mixed systems. 2. Express the Hamiltonian in a finite basis and see the dependence of observables with the basis size N. 3. The role of the system size in the scaling theory is played by N 4. For each system one has to map the quantum chaos problem onto an appropiate basis. For billiards, kicked rotors and quantum maps this is straightforward.

Universality in quantum chaos Bohigas-Giannoni-Schmit conjecture Classical chaos Wigner-Dyson Exceptions: Kicked systems and arithmetic billiards Berry-Tabor conjecture Classical integrability Poisson statistics Exceptions: Harmonic oscillator Systems with a degenerate spectrum Questions: 1. Are these exceptions relevant? 2. Are there systems not classically chaotic but still described by the Wigner-Dyson? 3. Are there other universality class in quantum chaos? How many?

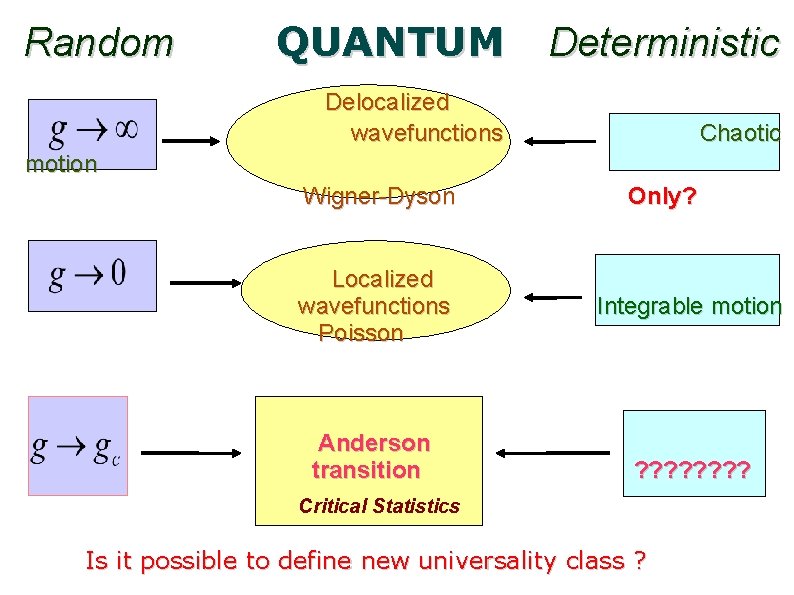
Random QUANTUM Deterministic Delocalized wavefunctions Chaotic motion Wigner-Dyson Localized wavefunctions Poisson Anderson transition Only? Integrable motion ? ? ? ? Critical Statistics Is it possible to define new universality class ?

Wigner-Dyson statistics in non-random systems 1. Evaluate the typical time needed to reach the boundary of the system. Take into account symmetries. In billiards it is just the ballistic travel time. In kicked rotors and quantum maps it is the time needed to explore a fixed basis. In billiards with some (Coulomb) a potential inside one can obtain this time by mapping the billiard onto an Anderson model. 2. Use the Heisenberg relation to estimate the Thouless energy and the dimesionless conductance g(N) as a function of the system size N (in momentum or position). IF Wigner-Dyson statistics applies

Anderson transition in non-random systems Conditions: 1. Between chaotic and integrable but not a superposition. 2. Classical anomalous diffusion 3. Quantum power-law localization Examples: 1 D: =1, de=1/2, Harper model =2, de=1, Kicked rotor with classical singularities, interval exchange maps. 2 D: =1, de=1, Coulomb billiard 3 D: =2/3, de=1, Kicked rotor at critical coupling

1 D kicked rotor with singularities Classical Motion Classical diffusion Step function Classical Anomalous Diffusion Quantum Evolution Power-law localization

1. >0 Localization Poisson 2. <0 Delocalization Wigner-Dyson 3. =0 L-D transition Critical statistics Anderson transition 1. log (1/f noise) and step singularities 2. Multifractality and Critical statistics. Results are stable under perturbations and sensitive to the removal of the singularity

Non-analytical potentials and the Anderson transition in deterministic systems Classical Input (1+1 D) Non-analytical chaotic potential 1. Fractal and homongeneous phase space (cantori) 2. Anomalous Diffusion in momentum space Quantum Output (AGG PRE 69 066216) Wavefunctions power-law localized 1. Spectral properties expressed in terms of P(k, t) 2. The case of step and log singularities (1/f noise) leads to: Critical statistics and multifractal wavefunctions Attention: KAM theorem does not hold and Mixed systems are excluded!

Analytical approach: From the kicked rotor to the 1 D Anderson model with long-range hopping Fishman, Grempel and Prange method: Dynamical localization in the kicked rotor is 'demonstrated' by mapping it onto a 1 D Anderson model with short-range interaction. Kicked rotor Anderson model What happens if Is there any relation between non-differentiability and Wr? Yes step

Non-differentiability induces long range hopping The associated Anderson model has long-range hopping depending on the nature of the non-analyticity: Already solved (Fyodorov, Mirlin, Seligman 1996, Levitov 1990) but long range hopping is now NOT random. Critical Cases 1. Log singularity Wr ~Aij/r with Aij pseudo-random Similar to Critical statistics . 2. Step like singularity Wr ~Aij/r with Semi-Poisson statistics (Harper model, pseudo integrable billiards) Exact treatment possible AGG PRE 2006 Experimental verification by using ultra-cold atoms techniques

How do we know that a metal is a metal? Texbook answer: Look at the conductivity or other transport properties Other options: Look at eigenvalue and eigenvectors 1. Eigenvector statistics: Dq = d Metal Dq = 0 Insulator 2. Eigenvalue statistics: Level Spacing distribution: Number variance: Dq = f(d, q) M-I transition

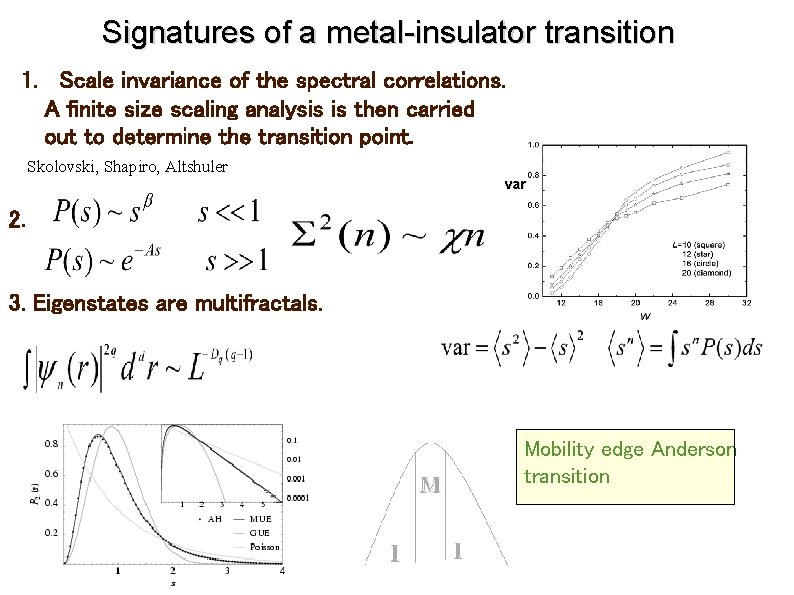
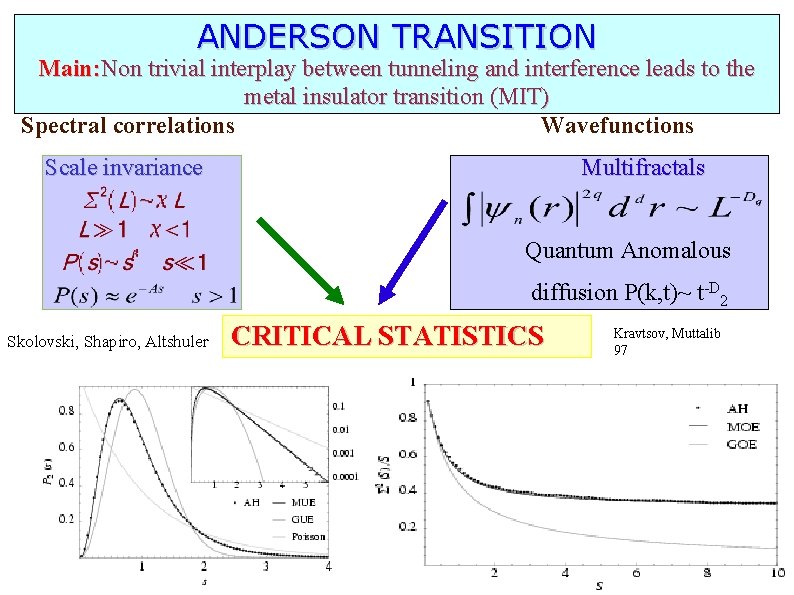
Signatures of a metal-insulator transition 1. Scale invariance of the spectral correlations. A finite size scaling analysis is then carried out to determine the transition point. Skolovski, Shapiro, Altshuler var 2. 3. Eigenstates are multifractals. Mobility edge Anderson transition

V(x)= log|x| =15 =8 =4 =2 Spectral χ =0. 026 χ =0. 057 χ=0. 13 χ=0. 30 Multifractal D 2= 0. 95 D 2= 0. 89 D 2 ~ 1 – 1/ D 2= 0. 72 D 2= 0. 5 Summary of properties 1. Scale Invariant Spectrum 2. Level repulsion 3. Sub-Poisson Number variance 4. Multifractal wavefunctions 5. Quantum anomalous diffusion ANDERSON TRANSITON IN QUANTUM CHAOS Ketzmerick, Geisel, Huckestein

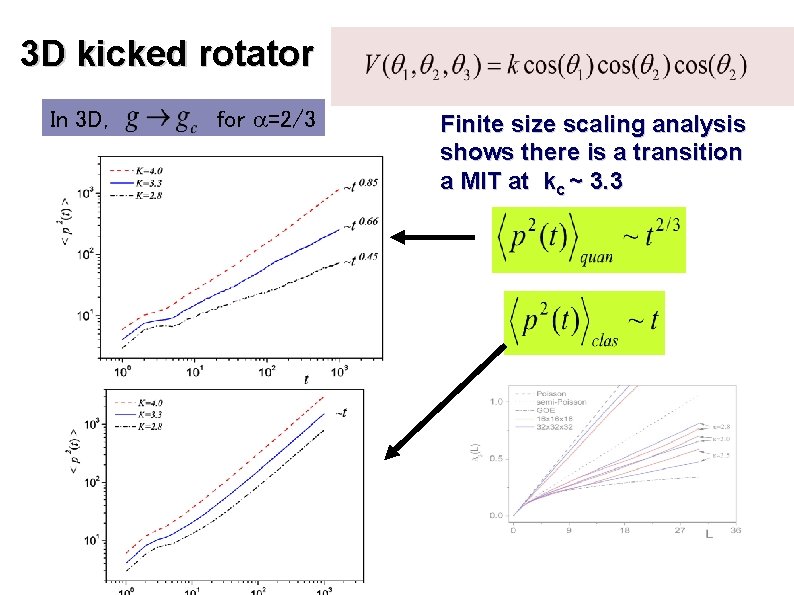
3 D kicked rotator In 3 D, for =2/3 Finite size scaling analysis shows there is a transition a MIT at kc ~ 3. 3

Experiments and 3 D Anderson transition Our findings for the 3 D kicked rotor at kc and 1 D with log singularities may be used to test experimentally the Anderson transition by using ultracold atoms techniques (Raizen). One places a dilute sample of ultracold Na/Cs in a periodic step-like standing wave which is pulsed in time to approximate a delta function the atom momentum distribution is measured. The classical singularity cannot be reproduced in the lab. However (AGG W Jiao 2006) an approximate singularity will still show typical features of a metal insulator transition

CONCLUSIONS 1. One parameter scaling theory is a valuable tool for the understading of universal features of the quantum motion. 2. Wigner Dyson statistics is related to classical motion such that 3. The Anderson transition in quantum chaos is related to 4. Experimental verification of the Anderson transition is possible with ultracold atoms techniques.

ANDERSON TRANSITION Main: Non trivial interplay between tunneling and interference leads to the metal insulator transition (MIT) Spectral correlations Wavefunctions Scale invariance Multifractals Quantum Anomalous diffusion P(k, t)~ t-D 2 Skolovski, Shapiro, Altshuler CRITICAL STATISTICS Kravtsov, Muttalib 97

Density of Probability

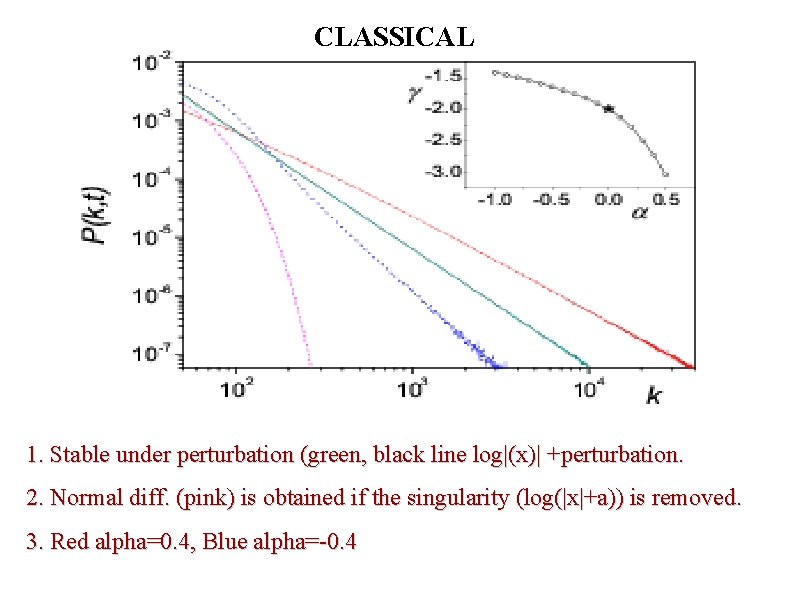
CLASSICAL 1. Stable under perturbation (green, black line log|(x)| +perturbation. 2. Normal diff. (pink) is obtained if the singularity (log(|x|+a)) is removed. 3. Red alpha=0. 4, Blue alpha=-0. 4

Classical-Quantum diffusion

ANDERSON-MOTT TRANSITION Main: Non trivial interplay between tunneling and interference leads to the metal insulator transition (MIT) Spectral correlations Wavefunctions Scale invariance Multifractals Skolovski, Shapiro, Altshuler CRITICAL STATISTICS Kravtsov, Muttalib 97 "Spectral correlations are universal, they depend only on the dimensionality of the space. " Mobility edge Mott Anderson transition

Multifractality Intuitive: Points in which the modulus of the wave function is bigger than a (small) cutoff M. If the fractal dimension depends on the cutoff M, the wave function is multifractal. Formal: Anomalous scaling of the density moments. Kravtsov, Chalker 1996

POINCARE SECTION P X

Is it possible a MIT in 1 D ? Yes, if long range hopping is permitted Eigenstates power-law localized Thermodynamics limit: Eigenstates Spectral Multifractal Critical statistics Localized Poisson statistics Delocalized Random Matrix Analytical treatment by using the supersymmetry method (Mirlin &Fyodorov) Related to classical diffusion operator.

Eigenfunction characterization 1. Eigenfunctions moments: 2. Decay of the eigenfunctions:

Looking for the metal-insulator transition in deterministic Hamiltonians What are we looking for? - Between chaotic and integrable but not a superposition. NOT mixed systems. 1 D and 2 D : Classical anomalous diffusion and/or fractal spectrum 3 D : Anomalous diffusion but also standard kicked rotor Different possibilities - Anisotropic Kepler problem. Wintgen, Marxer (1989) - Billiard with a Coulomb scatterer. Levitov, Altshuler (1997) - Generalized Kicked rotors, Harper model, Bogomolny maps

Return Probability

V(q) = log (q) t = 50 CLASSICAL

V(q)= 10 log (q)