Universal Introduction and Quantifier Exchange Rules Overview Universal

Universal Introduction and Quantifier Exchange Rules

Overview ¢ Universal Introduction English Example l The Logical Mechanics l Quantifier Exchange Rules ¢ Examples ¢

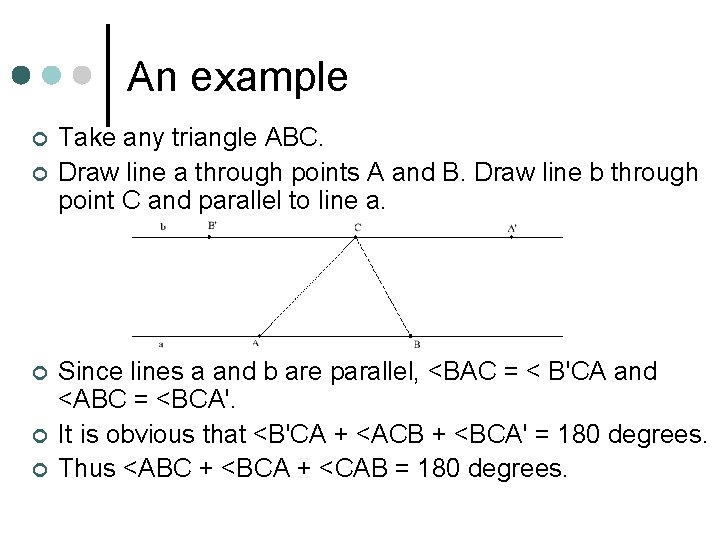
An example ¢ ¢ ¢ Take any triangle ABC. Draw line a through points A and B. Draw line b through point C and parallel to line a. Since lines a and b are parallel, <BAC = < B'CA and <ABC = <BCA'. It is obvious that <B'CA + <ACB + <BCA' = 180 degrees. Thus <ABC + <BCA + <CAB = 180 degrees.

Another example Take your typical journalist. ¢ He clearly has an incentive to report newsworthy events. ¢ Reporting on these events inevitably involves emphasizing previously unknown risks. ¢ Thus, journalists emphasize previously unknown risks. ¢

What exactly have we done here? ¢ We’ve taken a representative instance, and because it is representative, we draw a universal conclusion from it. Representative instances: Triangle ABC, “Your typical journalist” l Universal Conclusions: All triangles’ vertices sum to 180 degrees, All journalists emphasize risks. l ¢ This is the core of Universal Introduction ( I).

A closer look at the logic… 1. 2. 1. 2. 3. 4. x(Jx Ix) x(Ix Ex) x(Jx Ex) Ja Ia 1 E Ia Ea Ja Ea x(Jx Ex) 2 E 3, 4 HS 5 I A A Journalists have an incentive to report on newsworthy events. 2. Reporting on newsworthy events emphasizing risk. So journalists emphasize risk. 3. Your typical journalist has an incentive to report newsworthy events. 4. If he has this incentive, then he emphasizes risks. 5. So your typical journalist emphasizes risk. 6. So all journalists emphasize risk. 1.

The rule: I ¢ Let Ф be a formula ¢ x. Fx├ x(Fx v Gx) containing a name , and let 1. x. Fx Ф / be the result of A replacing all occurrences of in Ф by some variable 2. Fa 1 E not already in Ф. Then from 3. Ф infer Ф / , provided 4. that does not occur in any hypothesis whose hypothetical derivation has not yet ended or in any assumption. Fa v Ga x(Fx v Gx) 3 I 2 v. I

What you can’t do with I You cannot infer a universally quantified statement from a statement involving a name that occurs in any hypothesis whose hypothetical derivation has not yet ended or a name that occurs in any assumption. ¢ English Example: Khalifa is right handed. So everyone is right handed. ¢

The English Example made Formal ¢ ¢ 1. 2. ¢ Let k= Khalifa and Rx = x is right handed So the prohibition states that the following is INCORRECT: Rk A x. Rx 1 I That would be a hasty generalization, as should be obvious from the English.

Proof strategies ¢ ¢ If the main operator is →, ↔, v, &, or ~, don’t forget what you’ve already learned—they still hold good. If the main operator is , then first see if you can use I. If there are existentially quantified premises, you may have to first hypothesize for E before applying I. If the main operator is , first try to get the conclusion by I. If there are universal premises, you may have to first apply E before applying I. ~I remains a nuclear option.

Quantifier exchange rules: Examples ¢ ¢ All students are nice Not a single student is not nice. l Φ ~ ~Φ Some students are not nice Not all students are nice. l ~Φ ~ Φ All students are non-nice Not a single student is nice. l ~Φ ~ Φ Some students are nice Not all students are non-nice. l Φ ~ ~Φ

Quantifier exchange rules (QE, see Nolt, p. 238) Think of these as the functional equivalent of De. Morgan’s Laws (DM) applied to quantifiers ¢ You take a ~ and “distribute” it through a quantified statement, switching to (or vice versa), and placing the ~ on the other side of the quantifier. ¢ These are derived rules for predicate logic. ¢

Sample: Nolt 8. 4. 2. 2 x(Fx→Gx) ├ x. Fx → x. Gx 1. x(Fx → Gx) 2. | x. Fx 3. |Fa 4. |Fa→Ga 5. |Ga 6. | x. Gx 7. x. Fx → x. Gx A H for →I 2 E 1 E 3, 4 →E 5 I 2 -6 →I

8. 4. 2. 7 x(Fx→Gx), ~ x. Gx ├ x~Fx 1. x(Fx→Gx) 2. ~ x. Gx 3. x~Gx 4. Fa → Ga 5. ~Ga 6. ~Fa 7. x~Fx A A 2 QE 1 E 3 E 4, 5 MT 6 I

8. 4. 2. 10 x y. Rxy ├ y x. Rxy 1. x y. Rxy 2. | y. Ray 3. | Rab 4. | x. Rxb 5. | y x. Rxy 6. y x. Rxy A H for E 2 E 3 I 4 E 1, 2 -5 E