Universal Frequency Reference Presented first at Gippstech 2012

Universal Frequency Reference Presented first at Gippstech 2012 V 1. 11 Glen English VK 1 XX glen@pacificmedia. com. au

Frequency reference system Provides reference for any radio Low noise fundamental output 1 Hz – 150 MHz Provides 30 m. Hz steps with 125 MHz clock Locked to GPS, auto holdover Low Power (0. 5 -1. 5 W depending on power supply and output ) and 60 x 80 mm • Can be controlled/setup from PC • • •

Implementation • • • Any GPS provides 1 pulse per second Uses a DDS (direct digital synthesiser) Free running TCXO or OCXO provides clock Frequency of XO not critical Many XOs do not have external V ctl- not required.

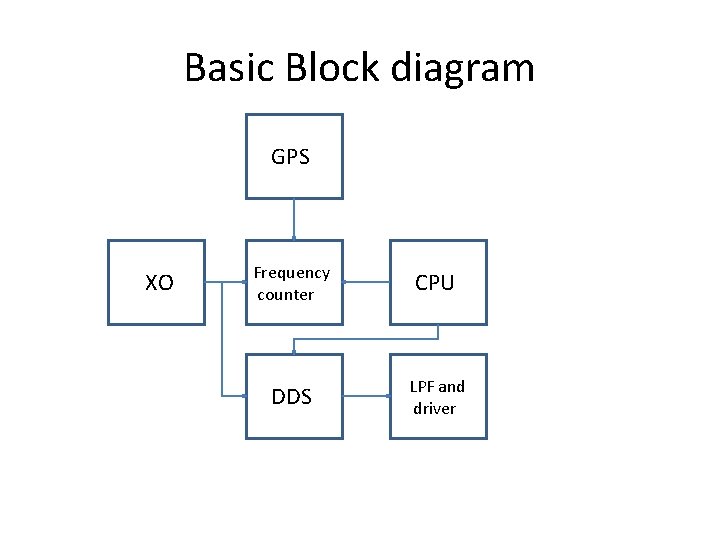
Basic Block diagram GPS XO Frequency counter CPU DDS LPF and driver

How DDS works (simplified) • Consists of a binary counter and an adder • The counter has a maximum value • The RF output is connected to the highest bit (MSB) of the counter. • A clock is input which every time there is a positive-going transition, a fixed value is added to the counter. • The amount added to the counter every ‘clock’ determines the how often the counter rolls over its maximum value

DDS counter • 4 bit binary counter being incremented with value of 3 every clock. • 0000, 0011, 0110, 1001, 1100, 1111, 0010, 0101, 1000, 1011, 1110, 0001, 0100, 0111, 1010, 1101 • 4 bit binary counter being increment with value of 1 every clock • 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 0000, 0001, 0010, 0011, 0100

DDS cont • Example • Counter with max value of 100 • If a clock adds a value of 5 at 1 MHz, what will be the rollover rate per second? • = (clock freq * step) / counter max (eq 1) • = (1, 000 * 5 ) / 100 • = 50, 000 times per second.

DDS cont 2 • • This DDS : can be clocked up to 400 MHz Has a rollover value of 2^32=4, 294, 967, 296 Allows for very precise frequency steps if used as a synthesiser Using (eq 1) 125 e 06 * 100, 000 / (2^32) = 2910. 383046 Hz 125 e 06 * 100, 001 / (2^32) = 2910. 41215 Hz Cosine lookup table is connected to the counter so that the DDS generates sine as well as square waves.

Frequency control • Precise DDS frequency steps allow us to use any source frequency for any output frequency • DDS has clock multiplier to further enhance flexibility. • But no control over frequency of source oscillator ? How do we lock this to the GPS ?

Frequency Counter • We count how many cycles of the fixed XO occur between 1 PPS from the GPS • If 63, 000, 005 oscillator cycles are counted for each 1 pps GPS pulse, the frequency must be 63, 000, 005 Hz • Now we know the frequency of the XO

CPU calculation • Think of DDS as a fractional divider (for the moment) • For 10 MHz output , we must program the DDS steps for (63, 000, 005 / 10, 000) • Which is 6. 3000005. which we can do…. • The XO frequency is measured every 2 seconds and the new ‘divisor’ (step) is applied to the DDS • Enables drift in XO to be compensated for • Averaging of different lengths are provided to enhance precision

Implementation • I figured this out when building WSPR DDS based exciters- I had odd frequency XOs available • PCB costs about $50 of bits depending on the type of oscillator used. • Better results with better quality oscillators -can work with $1 oscillator if does not change too much per update cycle. Proto used $4 125 MHz TCXO. • Care taken to ensure no feedthru noises from digital controller into oscillator.

CPU job : Count clocks per GPS 0. 5 pps pulse Update moving average Calculate actual XO frequency Calculate new Frequency Tuning Word Write to DDS

Outputs • • • PCB has: 100 m. W RF driver Opto isolated closures Serial port for config/ctl DAC output for audio tone generation Can accept any oscillator 5 to 125 MHz input

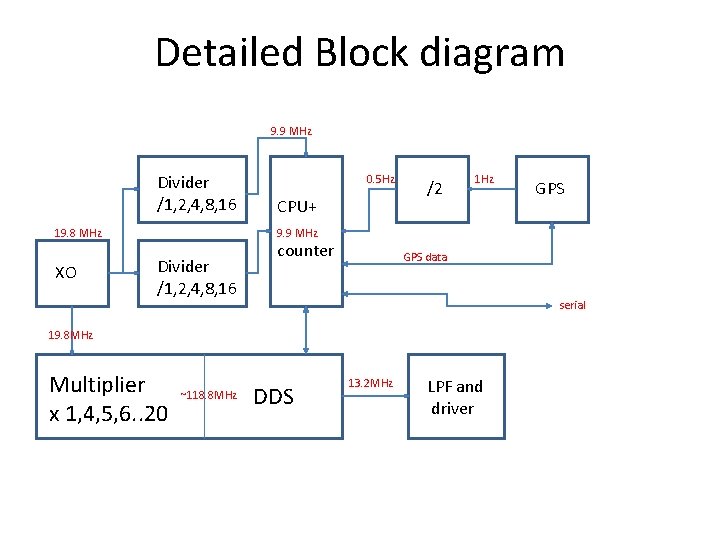
Detailed Block diagram 9. 9 MHz Divider /1, 2, 4, 8, 16 19. 8 MHz XO 0. 5 Hz CPU+ /2 1 Hz GPS 9. 9 MHz Divider /1, 2, 4, 8, 16 counter GPS data serial 19. 8 MHz Multiplier x 1, 4, 5, 6. . 20 ~118. 8 MHz DDS 13. 2 MHz LPF and driver

Jitter Notes • Jitter performance of output limited to jitter performance of source XO • DDS output inherently has jitter equal to the DDS clock on output – this is why we low pass filter • On board filter design important to reduce jitter • Use highest DDS clock (by using on-chip multiplier) to ease filtering requirements • Jitter important when reference is multiplied up to 10 GHz.

Limitations • It is basically a frequency counter. • Longer counting times will yield more precision. • Compared with counting for one second , If the number of cycles over 10 seconds are counted, there is 10 x the precision, as the ‘error’ produced is 10 x what it would have been over 1 second. • Or average the 1 second results over 10 seconds (take avg of 10 numbers) , -same though bias in the number crunching must be removed.

Oscillator limitations • Internal correction of some cheap TCXOs

Moving averages • Currently a moving average is used – • for each GPS 1 pps pulse, the last n counts are added together and divided by n. • Update is therefore on the fly, but incapable of tracking changes faster than the filter length because current estimate is made up of last n values. • Thermal drift limit is imposed on the XO • This goes for all disciplined oscillators

Accuracy and Precision • • Averaging improves error precision Accuracy is based on 1 pps GPS output Count 1, 000 cycles over 1 second = 1 Hz precision (1 ppm) Count 10, 000 cycles over 1 second = 0. 1 Hz precision (0. 1 ppm) Faster counters yield improved basic precision.

Improving precision • Higher precision per counter gate time (1 pps) yields better drift tracking capability. • Averaging improves precision but takes time • Sure we can get 0. 00001 ppm if we wait a long time. • Some applications required good precision hold and absolute frequency accuracy is unimportant. • Some applications required high accuracy – IE blind netting on 10 GHz.

XO Thermals • Averaging with drifting XO just takes average of the frequency over the drift. Moving average is behind the time. • Yes more precision due to averaging. • But drift over averaging period reduced accuracy. • 10 MHz 1 PPM XO (0 -70 C ) : if drifts 5 deg C • Drifts 0. 0714 ppm. A country mile

Drift calcs • 0. 0714 ppm. (5 deg C)Not a country mile if over days. • If 10 MHz counter clock, 0. 1 Hz precision per 1 second gate. • = 0. 1 ppm • Desired precision 0. 01 ppm = 10 sec averaging/counting. • Max thermal drift over 10 seconds is 0. 7 deg C.

Solution to drift problem • 2 nd order predictor • The future events can be predicted from the previous events • Useful for warm up / warm down drift • Non linear change with time variations OK • Not useful for random drift

Drift 2 • • • Solution to short term random drift Higher counter frequency 30 MHz counter clock = 0. 0333 ppm/ sec Vs 10 MHz clock = 0. 1 ppm/sec Averaging over long periods provides further precision but system can respond to short term drifts at high precision.

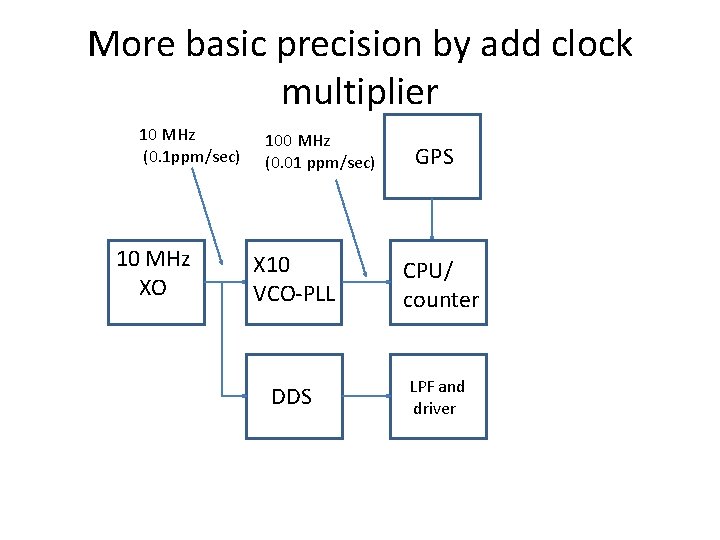
More basic precision by add clock multiplier 10 MHz (0. 1 ppm/sec) 10 MHz XO 100 MHz (0. 01 ppm/sec) GPS X 10 VCO-PLL CPU/ counter DDS LPF and driver

Next version • 48 bit DDS will provide 1 m. Hz control steps at 10 GHz • Higher counter speeds (32 MHz)/slave osc. • Predictor improvement. • Need to port 128 bit math lib to micro. • On board GPS receiver opt. (adds about $50) • High Z square wave output. • More flexible power supply

Extras • Also functions as a stand alone FSK style beacon – WSPR implemented. • Can connect to PC to provide steps smaller than CAT control provides for doppler tracking. - FT 817 10 Hz CAT steps example. • Radio will follow the reference frequency blindly. • Fast to get going (20 seconds after gps aq. ) • Can do chirps, FM, PSK, FSK

DDS tutorial : http: //www. analog. com/static/importedfiles/tutorials/450968421 DDS_Tutorial_rev 12 -2 -99. pdf