Units of Measurement OBJECTIVES Distinguish between a quantity

Units of Measurement

OBJECTIVES �Distinguish between a quantity, a unit, and a measurement standard. �Name and use SI units for length, mass, time, volume, and density. �Distinguish between mass and weight. �Perform density calculations. �Transform a statement of equality into a conversion factor.

KEY TERMS �Quantity �SI �Weight �Derived unti �Volume �Density �Conversion factor �Dimensional analysis

UNITS OF MEASUREMENT �Chef recipe �Measurements represent quantity �QUANTITY: is something has magnitude, size or amount. �Not the same as a measurement �EX: �A quantity represented by a teaspoon is volume �teaspoon measurement �Volume quantity

Scientists worldwide use SI measurements �Scientists all over the world have agreed on a single measurement system called Le Systéme International d’Unités, abbreviated SI. �Adopted in 1960 by General Conference on Weights and Measures � 7 base units �Most other units are derived �Non-SI units still commonly used

Scientists worldwide use SI measurements �SI units are defined in terms of standards of measurements. �Standards are objects or natural phenomena that are of a constant value, easy to preserve and reproduce, and particular in size. �International organizations monitor the defining process �US: National Institute of Standards and Technology (NIST) � 75 000 NOT 75, 000 � Becuase coma in other countries is used to represent the decimal point.

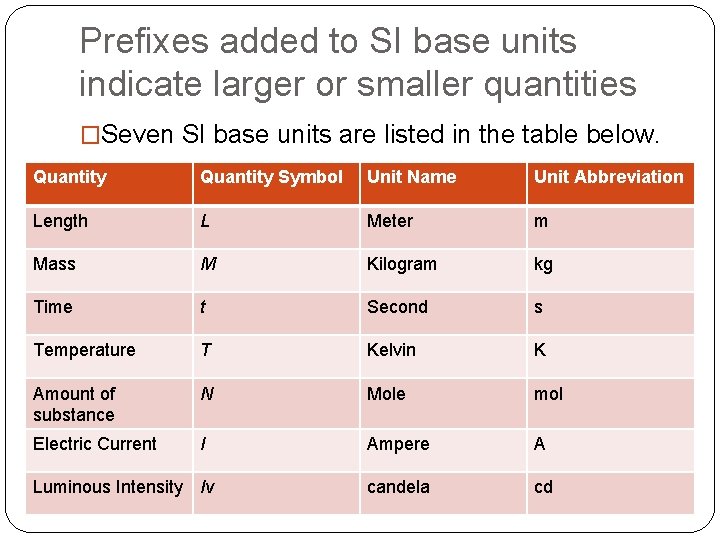
Prefixes added to SI base units indicate larger or smaller quantities �Seven SI base units are listed in the table below. Quantity Symbol Unit Name Unit Abbreviation Length L Meter m Mass M Kilogram kg Time t Second s Temperature T Kelvin K Amount of substance N Mole mol Electric Current I Ampere A candela cd Luminous Intensity Iv

Prefixes added to SI base units indicate larger or smaller quantities �All other SI units can be derived from these 7 fundamental units �Prefices added to the names of SI base unkits are used to represent quantities that are larger or smaller than the base units. �EX: �Prefix centi-, abreviated c, represents exponential factor 10 -2, which equals 1/100 � 1 centimeter 1 cm = 0. 01 m

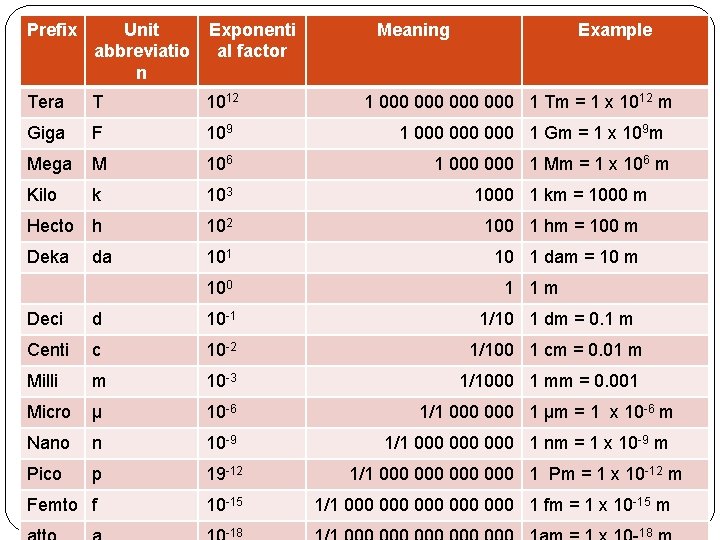
Prefix Unit abbreviatio n Exponenti al factor Tera T 1012 Giga F 109 Mega M 106 Kilo k 103 1000 1 km = 1000 m Hecto h 102 100 1 hm = 100 m Deka da 101 10 1 dam = 10 m 100 Meaning Example 1 000 000 1 Tm = 1 x 1012 m 1 000 000 1 Gm = 1 x 109 m 1 000 1 Mm = 1 x 106 m 1 1 m Deci d 10 -1 1/10 1 dm = 0. 1 m Centi c 10 -2 1/100 1 cm = 0. 01 m Milli m 10 -3 1/1000 1 mm = 0. 001 Micro µ 10 -6 1/1 000 1 µm = 1 x 10 -6 m Nano n 10 -9 1/1 000 000 1 nm = 1 x 10 -9 m Pico p 19 -12 Femto f 10 -15 -18 1/1 000 000 1 Pm = 1 x 10 -12 m 1/1 000 000 000 1 fm = 1 x 10 -15 m 18

Mass � MASS: a measure of the quantity of matter � SI standard base unit for mass is kilogram � Standard of mass are used to calibrate balances all over the world �The unit of mass equal to the mass of the international prototype of the kilogram � A kilogram is 2. 2 pounds � The gram, g, is 1/1000 of a kilogram �More useful for measurement of small objects �About the mass of a paper clip � Milligram, mg, used for tiny quantities � 1/1000 of a gram

Mass vs. Weight �Mass often confused with weight �Mass measure of the amount of matter �WEIGHT: a measure of the gravitational pull of matter. �Mass determined by comparing the mass of an object with a set of standard masses on two sides of the balance. �When mass on each are the same, the sides balance. �Mass does not depend on the gravity �Weight changes as gravitational forces change �Mass does not change

Mass vs. Weight �Mass measured on instrument called a balance �Weight typically measured on a spring scale �Involves reading the amount that an object pulls down on a spring �As force of gravity increases on an object , the object´s weight increases. �Weight of an object on the Moon is about 1/6 of weight on Earth.

Length �SI standard unit for length is the meter � 1 m is about the width of an average doorway �For longer distances, a kilometer is used � 1 km = 1000 m �For shorter distances, a centimeter is used �About the size of a paper clip � 1 cm = 1/100 m

SI base units combine to form derived units �Combinations of SI base units form DERIVED UNITS. �Produced by multipying or dividing standard units �EX: �Area length times width m x m = m 2

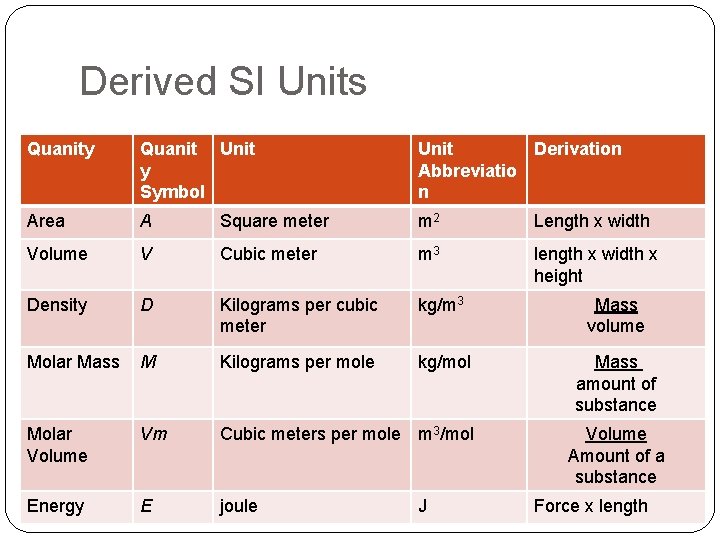
Derived SI Units Quanity Quanit Unit y Symbol Unit Derivation Abbreviatio n Area A Square meter m 2 Length x width Volume V Cubic meter m 3 length x width x height Density D Kilograms per cubic meter kg/m 3 Mass volume Molar Mass M Kilograms per mole kg/mol Mass amount of substance Molar Volume Vm Cubic meters per mole m 3/mol Energy E joule J Volume Amount of a substance Force x length

SI base units combine to form derived units �Some combinations of units are given their own names �Pressure �kg/m·s 2 �Pascal, Pa �Prefixes also added to derived units �Area �cm 2 or mm 2

Volume � VOLUME is the amount of space occupied by an object. � Derived SI unit of volume is cubic meters, m 3. � Large unit inconvenient in chemistry lab �Cubic centimeter, cm 3 � 1 m 3 = 1 000 cm 3 � Chemists use non-SI units for liquids and gases �Liter, L � 1 L = 1000 cm 3 �Milliliter, m. L � For smaller volume � 1000 m. L = 1 L � Cubic centimeter and milliliter are interchangeable

Density �Cork lighter than lead even though same size �Liquid mercury heavier than water �Different substances contain different masses per volume �DENSITY is the ratio mass to volume, or mass divided by volume DENSITY density = mass volume

DENSITY

Density �SI unit for density is devied from the base units for mass and volume �kg/m 3 �Units are large for laboratory use �g/cm 3 or g/m. L �Physical property of a substance �Doesn´t depend on amount of sample �As mass increases, volume increases (proportional) �Ratio of mass to volume is constant �Helps to identify a substance

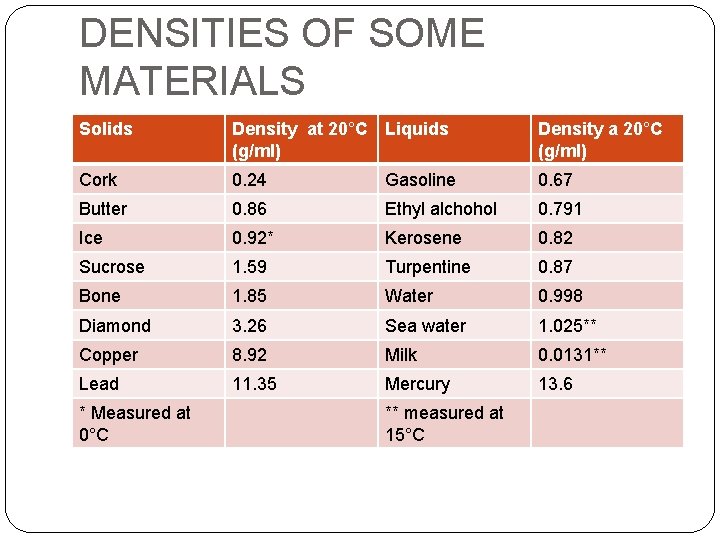
DENSITIES OF SOME MATERIALS Solids Density at 20°C Liquids (g/ml) Density a 20°C (g/ml) Cork 0. 24 Gasoline 0. 67 Butter 0. 86 Ethyl alchohol 0. 791 Ice 0. 92* Kerosene 0. 82 Sucrose 1. 59 Turpentine 0. 87 Bone 1. 85 Water 0. 998 Diamond 3. 26 Sea water 1. 025** Copper 8. 92 Milk 0. 0131** Lead 11. 35 Mercury 13. 6 * Measured at 0°C ** measured at 15°C

Sample Problem: Density �A sample of alumininum metal has a mass of 8. 4 g. The volume of the sample is 3. 1 cm 3. Calculate the density of aluminum �ANALYZE �m = 3. 4 g, v = 3. 1 cm 3, d =? �PLAN �Density = mass/volume �SOLVE �Density = 8. 4 g/ 3. 1 cm 3 = 2. 7 g/cm 3 �CHECK YOUR WORK

Practice Problems: Density 1. What is the density of a block of marble that occupies 310. cm 3 and has a mass of 853 g? 2. Diamond has a density of 3. 26 g/cm 3. What is the mass of a diamond that has a volume of 0. 351 cm 3. 3. What is the volume of a sample of liquid mercury that has a mass of 76. 2 g, given that the density of mercury is 13. 6 g/m. L?

Conversion Factors change one unit to another �A CONVERSION FACTOR is a ratio derived from the equality between two different units that can be used to convert from one unit to the other. �ALWAYS equals 1 �Have to equivalent to each other �EX: �How many quarter are there in a dollar?

Conversion Factors change one unit to another �Use conversion factors to solve problems through dimensional analysis �DIMENSIONAL ANALYSIS is a mathematical technique that allows you to use units to solve problems involving measurements. �Quantity sought = quantity given x conversion factor

Deriving Conversion Factors �You can derive conversion factors if you know the relationship between the unit you have and the unit you want. �Deci- means “ 1/10”, its 1/10 of a meter � 1 m = 10 dm

Sample Problem: Conversion Factors �Express a mass of 5. 712 g in mg and kg. �ANALYZE � 1 g = 1000 mg, 1 kg = 1000 g � 5. 712 g �PLAN �SOLVE � 5. 712 g x (1000 mg/1 g) = 5712 mg � 5. 712 g x (1 kg/1000 mg) = 0. 005712 kg �CHECK YOUR WORK

Practice: Conversion Factors 1. Express a length of 16. 45 m in centimeters and in kilometers. 2. Express a mass of 0. 014 mg in grams.