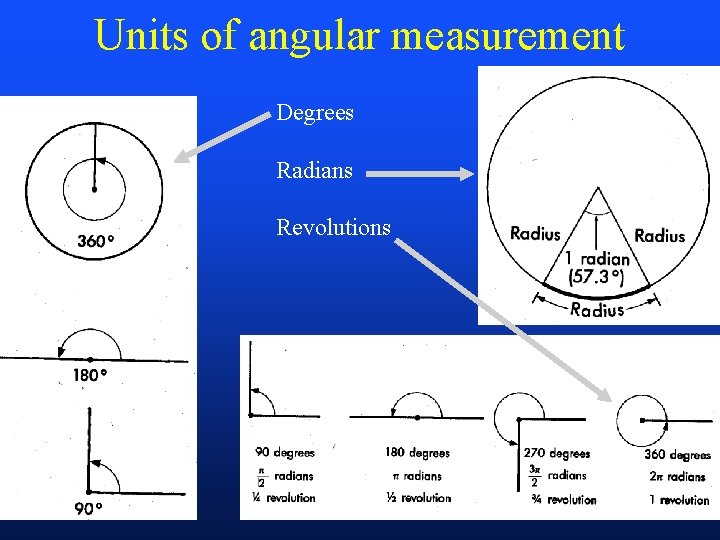
Units of angular measurement Degrees Radians Revolutions Tangential

Units of angular measurement Degrees Radians Revolutions

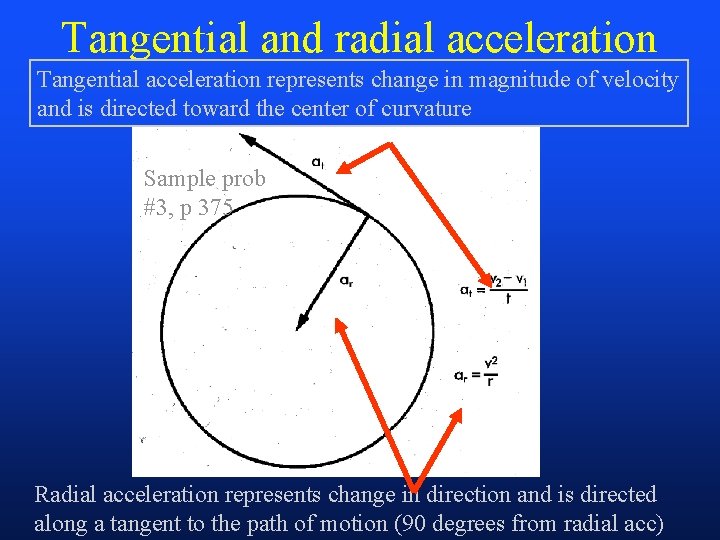
Tangential and radial acceleration Tangential acceleration represents change in magnitude of velocity and is directed toward the center of curvature Sample prob #3, p 375 Radial acceleration represents change in direction and is directed along a tangent to the path of motion (90 degrees from radial acc)

Linear Kinetics Objectives • Identify Newton’s laws of motion and gravitation and describe practical illustrations of the laws • Explain what factors affect friction and discuss the role of friction in daily activities and sports • Define impulse and momentum and explain the relationship between them • Explain what factors govern the outcome of a collision between two bodies • Discuss the interrelationship among mechanical work, power, and energy • Solve quantitative problems related to kinetic concepts

Linear Kinetics Outline - The Relationship between force and motion • • Read Chapter 12 in text Classification of forces Types of forces encountered by humans Force and motion relationships – Instantaneous effect – Newton’s law of acceleration (F=ma) – Force applied through time (Impulse-momentum) • Conservation of Momentum – Force applied through distance (work-energy) • Conservation of Energy • Self-study problems – Sample problems: #2 p 392; #3 p 396, #4 p 397, #5 p 402, #6 p 405, #7 p 408 – Introductory problems, p 411: 1, 3, 5, 7, 8, 10 • Homework problems (Due Monday, April 26) – Additional problems, p 412: 6, 8, 9

Effect of forces on the system • • Action vs reaction Internal vs external Motive vs resistive Force resolution – horizontal and vertical components • Simultaneous application of forces – determining the net force through vector summation

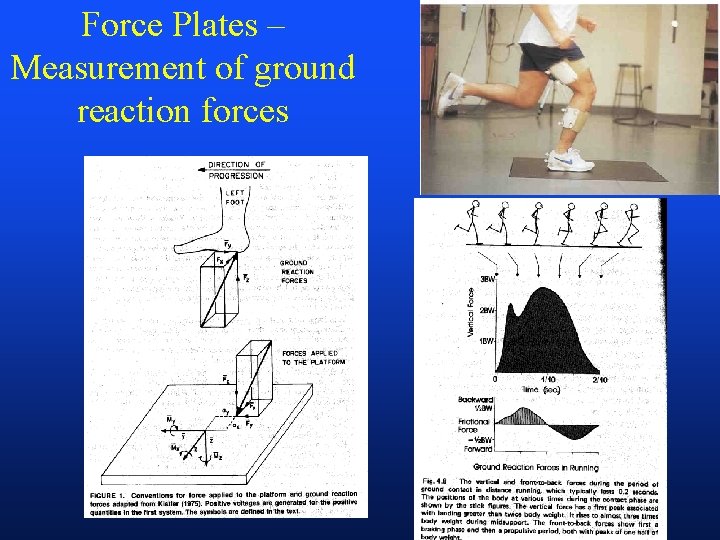
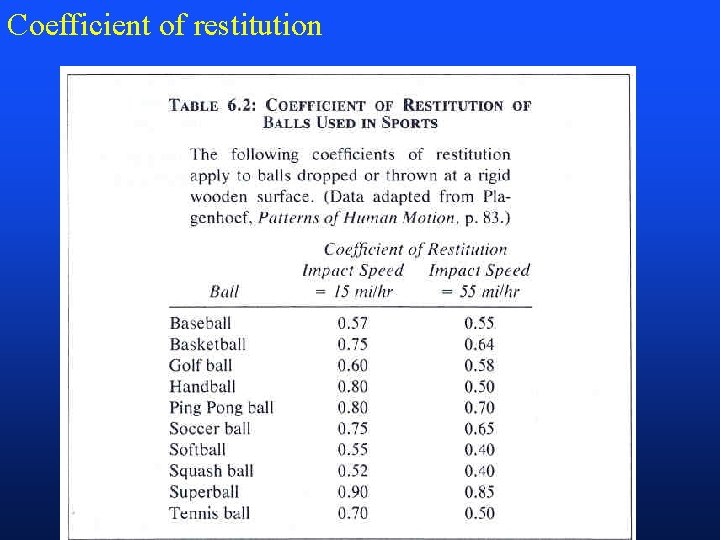
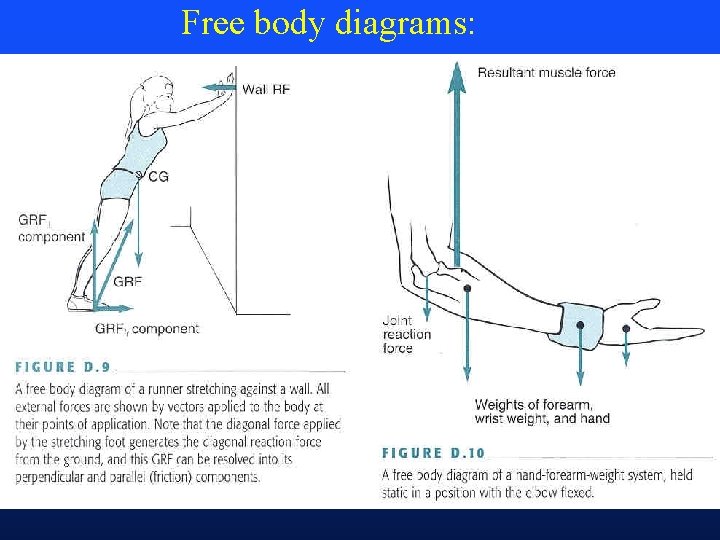
External forces commonly encountered by humans • Gravitational force (weight = mg) • Ground Reaction Force (GRF)(Figure 12 -4, p 386) – Vertical – Horizontal (frictional) • Frictional force (coefficient of friction) (pp 389 -395) • Elastic force (coefficient of restitution) (pp 399 -402) • Free body diagram - force graph (p 63)

Force Plates – Measurement of ground reaction forces

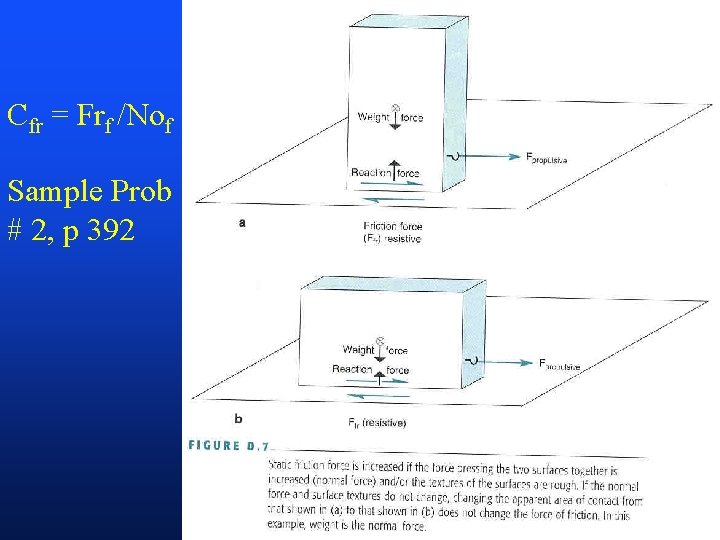
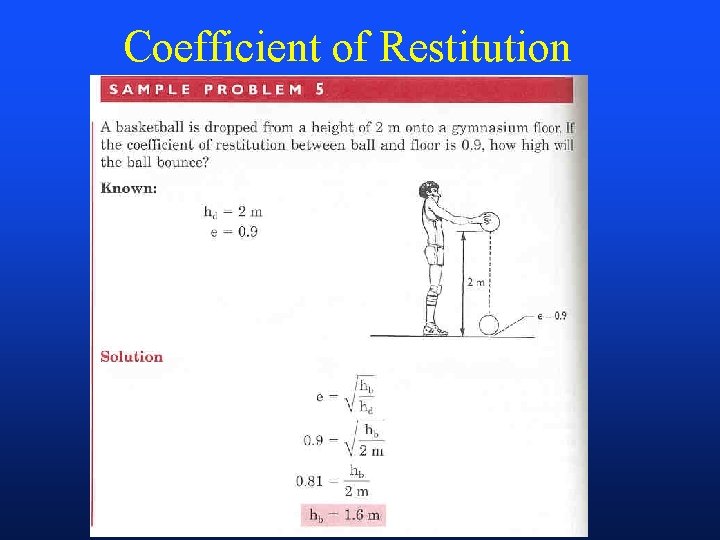
Cfr = Frf /Nof Sample Prob # 2, p 392

Coefficient of Restitution

Coefficient of restitution

Free body diagrams:

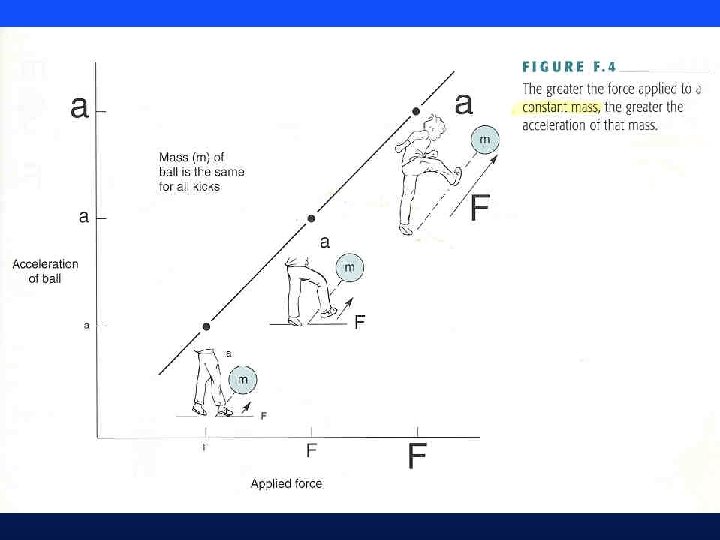
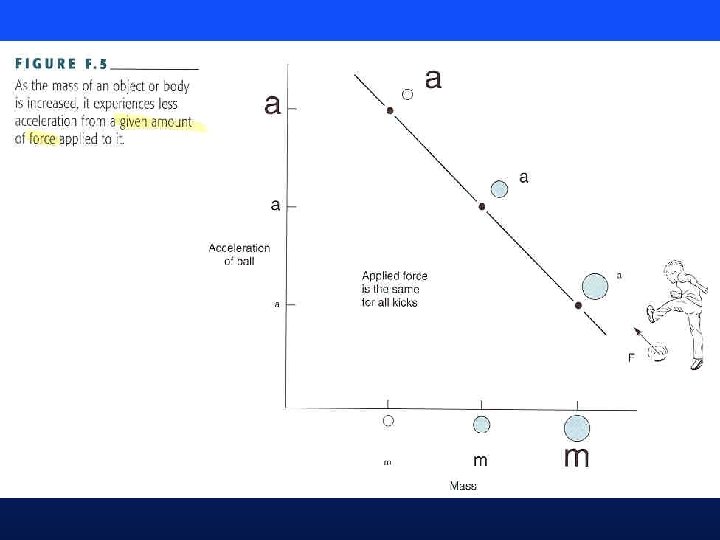
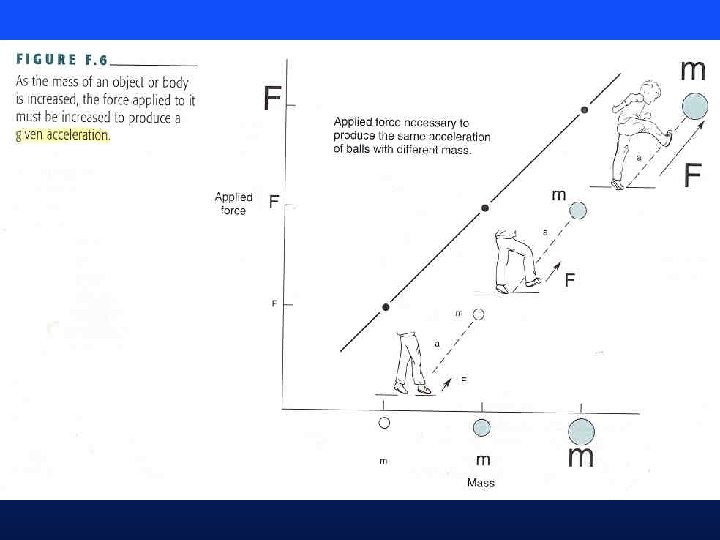
Instantaneous Effect of Force on an Object • Remember the concept of net force? • Need to combine, or add forces, to determine net force • Newton’s third law of motion (F = ma) • Inverse dynamics – estimating net forces from the acceleration of an object • Illustrations from Kreighbaum: Figures F. 4, F. 5, and F. 6 (pp 283 -284)

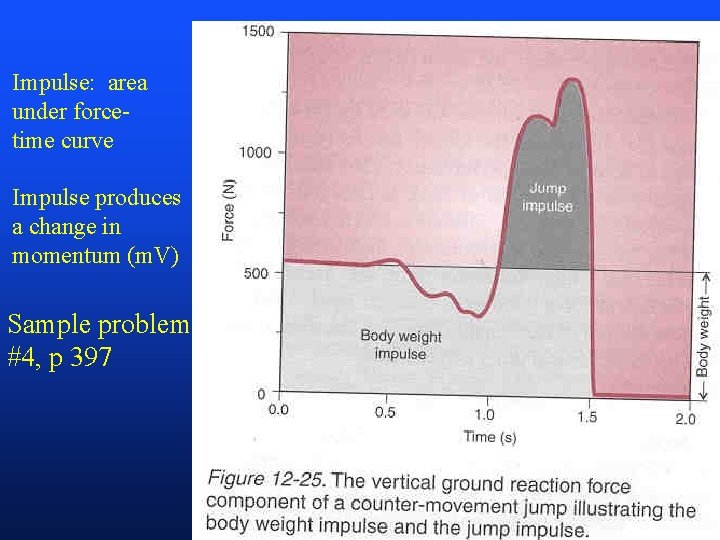
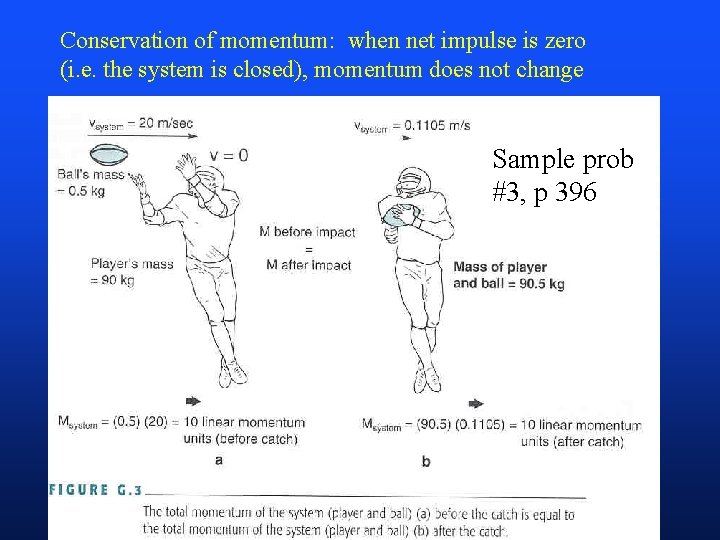
Force Applied Through a Time: Impulse. Momentum Relationship (pp 295 -399) • • Force applied through a time Impulse - the area under the force-time curve Momentum - total amount of movement (mass x velocity) An impulse applied to an object will cause a change in its momentum (Ft = mv) • Conservation of momentum (collisions, or impacts) – in a closed system, momentum will not change – what is a closed system?

Impulse: area under forcetime curve Impulse produces a change in momentum (m. V) Sample problem #4, p 397

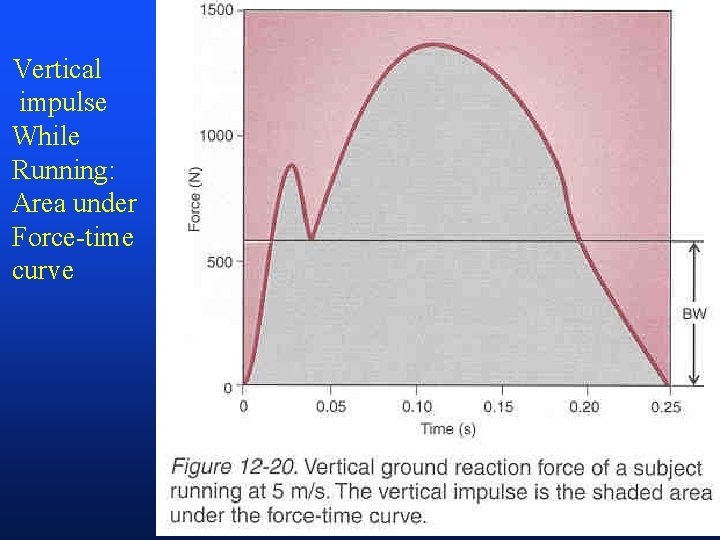
Vertical impulse While Running: Area under Force-time curve

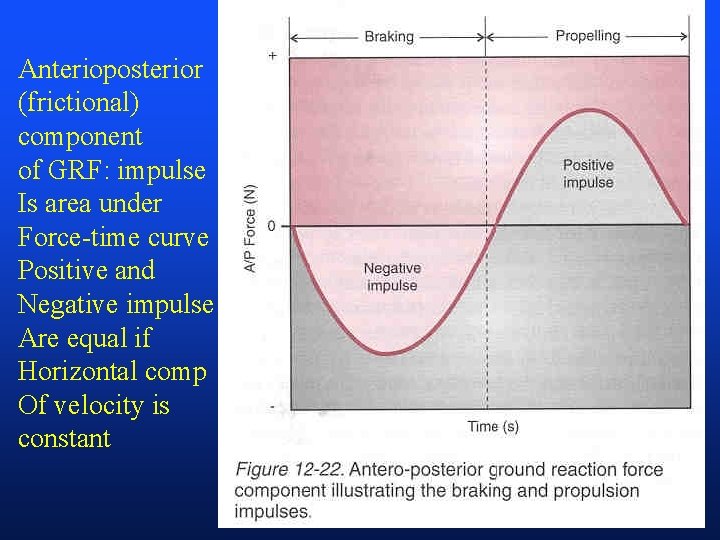
Anterioposterior (frictional) component of GRF: impulse Is area under Force-time curve Positive and Negative impulse Are equal if Horizontal comp Of velocity is constant

Conservation of momentum: when net impulse is zero (i. e. the system is closed), momentum does not change Sample prob #3, p 396

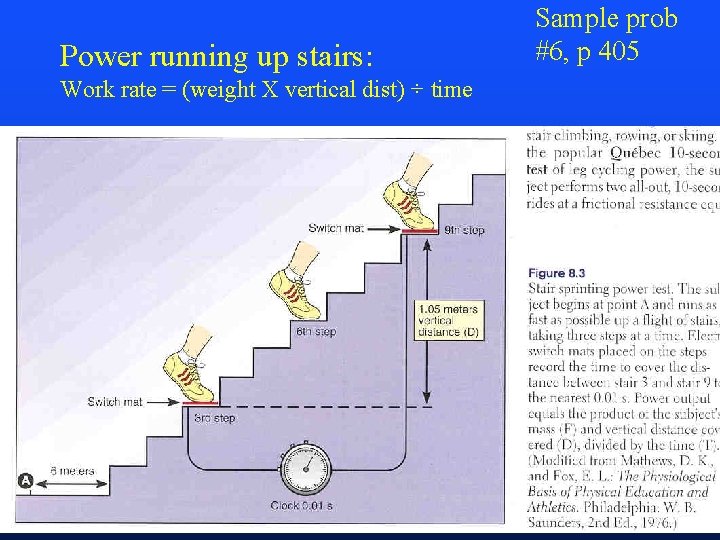
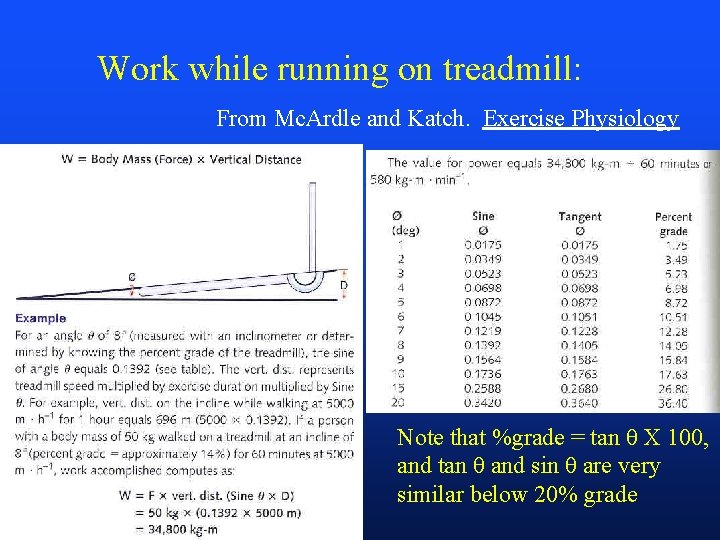
Force Applied Through a Distance: Work, Power, Energy (pp 403 -409) • Work - force X distance (Newton-meters, or Joules) – On a bicycle: Work = F (2 r X N) – On a treadmill: Work = Weightd X per cent grade – Running up stairs: Work = Weightd • Power - work rate, or combination of strength and speed (Newton-meters/second, or watts) – On a treadmill: P = Weightd X per cent grade/ time – On a bicycle: P = F (2 r X N) / time – Running up stairs: Work = Weightd /time (See next slide) • Energy - capacity to do work – kinetic, the energy by virtue of movement (KE = 1/2 mv 2 ) – gravitational potential, energy of position (PE = weight x height) – elastic potential, or strain, energy of condition (PE = Fd)

Power running up stairs: Work rate = (weight X vertical dist) ÷ time Sample prob #6, p 405

Work while running on treadmill: From Mc. Ardle and Katch. Exercise Physiology Note that %grade = tan θ X 100, and tan θ and sin θ are very similar below 20% grade

Homework: Calculating Power on a Treadmill • Problem: What is workload (power) of a 100 kg man running on a treadmill at 10% grade at 4 m/s? • Solution: – Power = force x velocity – Force is simply body weight, or 100 x 9. 8 = 980 N – Velocity is vertical velocity, or rate of climbing • Rate of climbing = treadmill speed x percent grade = 4 m/s x. 1 =. 4 m/s – Workload, workrate, or power = 980 N X. 4 m/s = 392 Watts • Note: 4 m/s = 9 mph, or a 6 min, 40 sec mile • Calculate your workload if you are running on a treadmill set at 5% grade and 5 m/s. – Answer for 200 lb wt (91 kg) is: 223 Watts

Conservation of Energy • In some situations, total amount of mechanical energy (potential + kinetic) does not change – Stored elastic energy converted to kinetic energy • • diving board bow (archery) bending of pole in pole vault landing on an elastic object (trampoline) – Gravitational potential energy converted to kinetic energy • Falling objects • Videodisk on pole vault

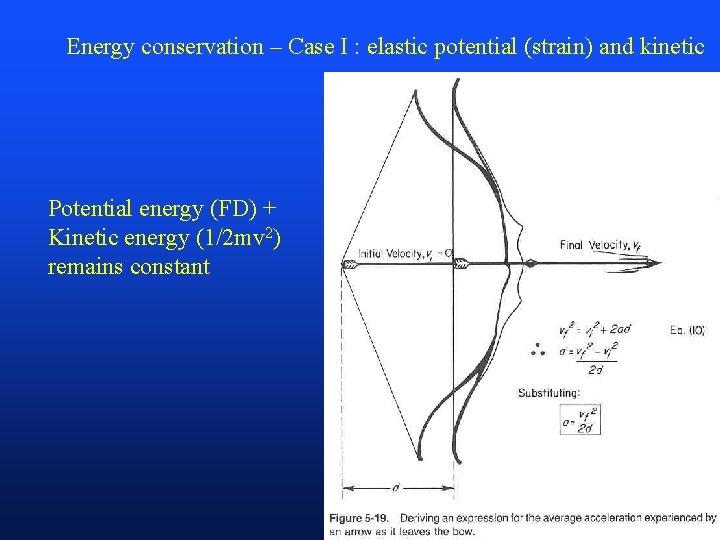
Energy conservation – Case I : elastic potential (strain) and kinetic Potential energy (FD) + Kinetic energy (1/2 mv 2) remains constant

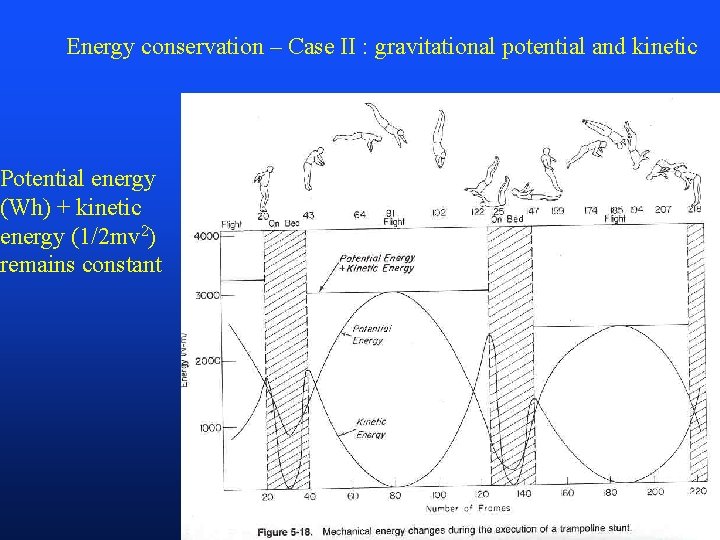
Energy conservation – Case II : gravitational potential and kinetic Potential energy (Wh) + kinetic energy (1/2 mv 2) remains constant

Linear Kinetics Formulae