Units and Measurement Chemistry Science 3 rd ESO

Units and Measurement Chemistry Science 3 rd. ESO

A) SI Units, Scientific Notation, Measurement, Accuracy, Precision, Error

Math and Units n Math- the language of Science n SI Units – International System ¨ MKS n. Meter m n. Mass kg n. Time s n National Bureau of Standards n Prefixes

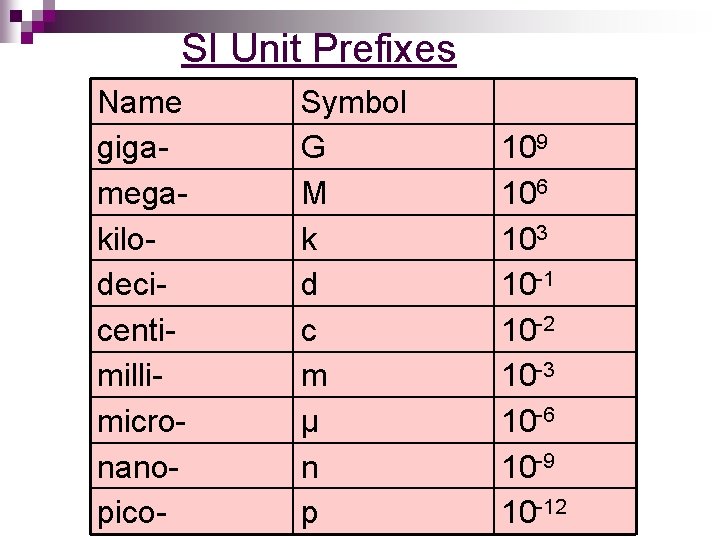
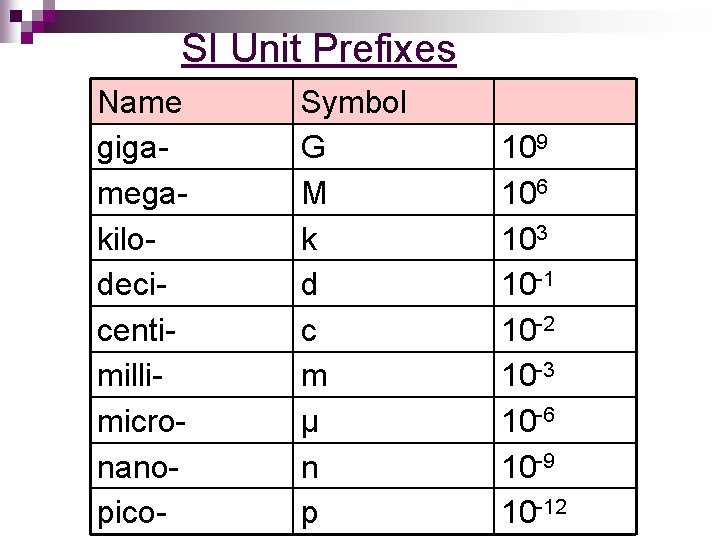
SI Unit Prefixes Name gigamegakilodecicentimillimicronanopico- Symbol G M k d c m μ n p 109 106 103 10 -1 10 -2 10 -3 10 -6 10 -9 10 -12

n Length

Metric Units The basic unit of length in the metric system in the meter and is represented by a lowercase m. Standard: The distance traveled by light in absolute vacuum in 1⁄299. 792. 458 of a second. Metric Units 1 Kilometer (km) = 1000 meters 1 Meter = 100 Centimeters (cm) Click the image to watch a short video about the meter. 1 Meter = 1000 Millimeters (mm) Which is larger? A. 1 meter or 105 centimeters C. 12 centimeters or 102 millimeters B. 4 kilometers or 4400 meters D. 1200 millimeters or 1 meter

Measuring Length How many millimeters are in 1 centimeter? 1 centimeter = 10 millimeters What is the length of the line in centimeters? _______cm What is the length of the line in millimeters? _______mm What is the length of the line to the nearest centimeter? ____cm HINT: Round to the nearest centimeter – no decimals. Ruler: http: //www. k 12 math. com/math-concepts/measurement/ruler-cm. jpg

Measuring Instruments Measuring Tapes: Long distance (up to 1 metre) are available in closed and open reel configurations. The open reel is good for outside or dirty environments. Calibrations are in centimetres or in millimetres. Straight Rules: Straight rules available in a large variety of materials, scales and graduations. Lengths typically don't exceed 1 m. It is used to measure in centimetres of length. Calliper rule A variation to the more traditional caliper is the inclusion of a vernier scale; this makes it possible to directly obtain a more precise measurement. Vernier calipers can measure internal dimensions (using the uppermost jaws in the picture at right), external dimensions using the pictured lower jaws, and depending on the manufacturer, depth measurements by the use of a probe that is attached to the movable head and slides along the centre of the body. The vernier scales may include both metric and inch measurements on the upper and lower part of the scale. Vernier calipers commonly used in industry provide a precision to a hundredth of a millimetre (10 micrometres), or one thousandth of an inch.

n Mass

Metric Units Mass refers to the amount of matter in an object. The base unit of mass in the metric system in the kilogram and is represented by kg. Standard: 1 kilogram is equal to the mass of the International Prototype Kilogram (IPK), a platinumiridium cylinder kept by the BIPM at Sèvres, France. Metric Units 1 Kilogram (kg) = 1000 Grams (g) Kilogram Prototype Click the image to watch a short video about mass. 1 Gram (g) = 1000 Milligrams (mg) Which is larger? A. 1 kilogram or 1500 grams C. 12 milligrams or 12 kilograms B. 1200 milligrams or 1 gram D. 4 kilograms or 4500 grams

Measuring Mass We will be using triple-beam balances to find the mass of various objects. The objects are placed on the scale and then you move the weights on the beams until you get the lines on the right-side of the scale to match up. Once you have balanced the scale, you add up the amounts on each beam to find the total mass. What would be the mass of the object measured in the picture? _______ + _______ = ____ g

Measuring Mass – Triple-Beam Balance 1 st – Place the film canister on the scale. 2 nd – Slide the large weight to the right until the arm drops below the line. Move the rider back one groove. Make sure it “locks” into place. 3 rd – Repeat this process with the top weight. When the arm moves below the line, back it up one groove. 4 th – Slide the small weight on the front beam until the lines match up. 5 th – Add the amounts on each beam to find the total mass to the nearest tenth of a gram. Click here to try an online activity.

n Volume

Metric Units Volume is the amount of space an object takes up. The base unit of volume in the metric system in the liter and is represented by L or l. Standard: 1 liter is equal to one cubic decimeter Metric Units 1 liter (L) = 1000 milliliters (m. L) 1 milliliter (m. L) = 1 cm 3 (or cc) = 1 gram* Which is larger? A. 1 liter or 1500 milliliters B. 200 milliliters or 1. 2 liters C. 12 cm 3 or 1. 2 milliliters* Click the image to watch a short video about volume.

Measuring Instruments Differentiate volumecapacity Volume and capacity are sometimes distinguished, with capacity being used for how much a container can hold (with contents measured commonly in litres or its derived units), and volume being how much space an object displaces (commonly measured in cubic metres or its derived units).

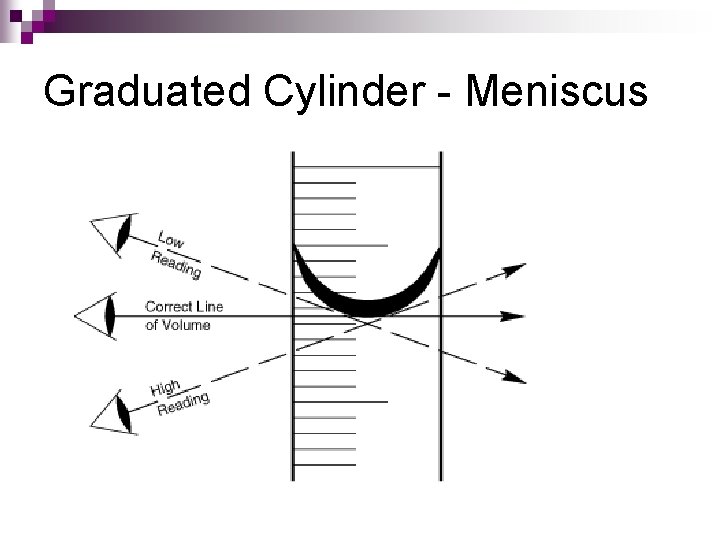
Measuring Volume We will be using graduated cylinders to find the volume of liquids and other objects. Read the measurement based on the bottom of the meniscus or curve. When using a real cylinder, make sure you are eye-level with the level of the water. What is the volume of water in the cylinder? _____ml What causes the meniscus? A concave meniscus occurs when the molecules of the liquid attract those of the container. The glass attracts the water on the sides.

Parallax error Parallax Error Parallax is a deceptive change of the position of an object which is observed while the position of the observer changes. Position of eye at all volumetric vessels must be at the same level as the meniscus. If not, the parallax will cause an error while reading the position of the meniscus of a liquid in a burette. It will be a positive mistake if the eye is lower, and negative if the eye is higher than the meniscus plane. If you are measuring the volume of liquid in a measuring cylinder for example, make sure you positioned your eye to take readings at the bottom of menicus for water and top of menicus for mercury.

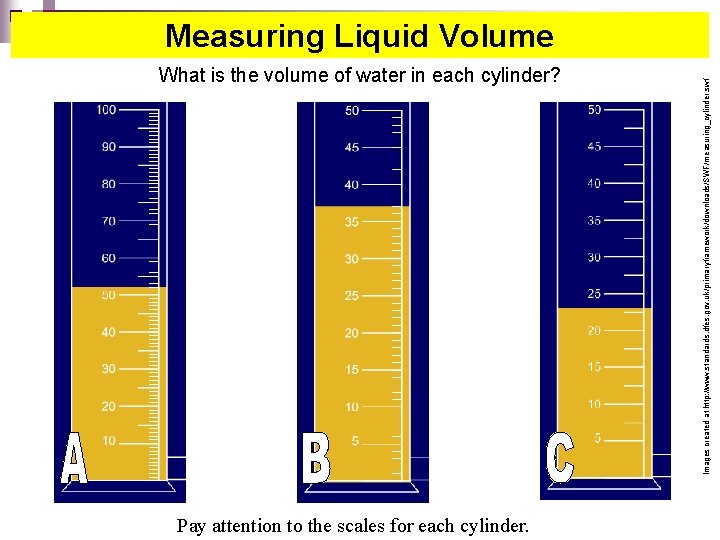
What is the volume of water in each cylinder? Pay attention to the scales for each cylinder. Images created at http: //www. standards. dfes. gov. uk/primaryframework/downloads/SWF/measuring_cylinder. swf Measuring Liquid Volume

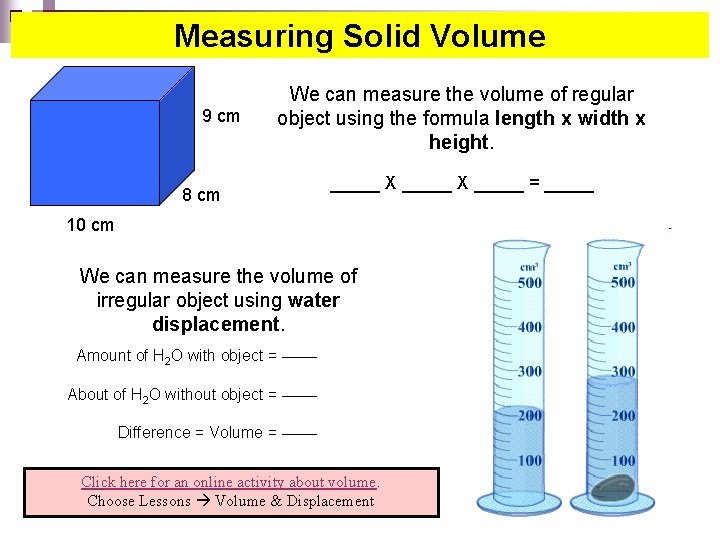
Measuring Solid Volume 9 cm We can measure the volume of regular object using the formula length x width x height. 8 cm _____ X _____ = _____ 10 cm We can measure the volume of irregular object using water displacement. Amount of H 2 O with object = ______ About of H 2 O without object = ______ Difference = Volume = ______ Click here for an online activity about volume. Choose Lessons Volume & Displacement

Scientific Notation n M x 10 n M is the coefficient 1<M<10 n 10 is the base n n is the exponent or power of 10

Other Examples: 5, 45 E+6 5, 45 x 10^6

Numbers less than 1 will have a negative exponent. A millionth of a second is: 0, 000001 sec 1, 0 E-6 1 x 10 -6 1, 0 x 10^-6

Limits of Measurement n Accuracy and Precision

n Accuracy - a measure of how close a measurement is to the true value of the quantity being measured.

Example: Accuracy n Who is more accurate when measuring a book that has a true length of 17, 0 cm? Susan: 17, 0 cm; 16, 0 cm; 18, 0 cm; 15, 0 cm Amy: 15, 5 cm; 15, 0 cm; 15, 2 cm; 15, 3 cm

n Precision – a measure of how close a series of measurements are to one another. A measure of how exact a measurement is.

Example: Precision Who is more precise when measuring the same 17, 0 cm book? Susan: 17, 0 cm; 16, 0 cm; 18, 0 cm; 15, 0 cm Amy: 15, 5 cm; 15, 0 cm; 15, 2 cm; 15, 3 cm

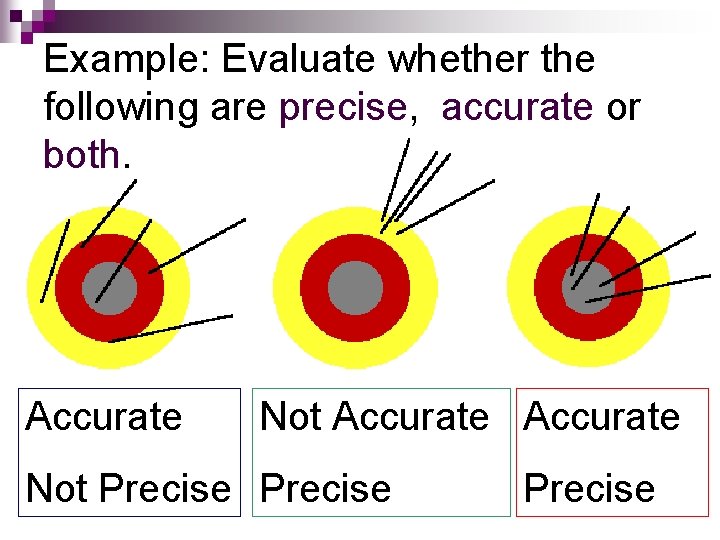
Example: Evaluate whether the following are precise, accurate or both. Accurate Not Precise

Accurancy Absolute error n Relative error n Precision= Significant Figures

Absolute Error= experimental –accepted value It is the amount of physical error in a measurement. It uses the same units than the measurement.

Relative error (Percent Error) % Error= |experimental –accepted| x 100 accepted value (value of thing measured) Relative error gives an indication of how good a measurement is relative to the thing being measured. If a have two students measuring two objects with a metre stick the comparative accurancy of these measurements can be determined by looking at their relative error.

Absolute- relative error Students measured time in an experiment. These measurements are: 3, 01 s; 3, 11 s; 3, 20 s; 3, 15 s n True value? (Valor que se considera exacto) n Absolute and relative error for each measurement? Measurement Absolute Error Relative Error 3, 01 s 3, 01 - 3, 12 = - 0, 11 s -0, 11 / 3, 12 = - 0, 036 (- 3, 6%) 3, 11 s 3, 11 -3, 12 = - 0, 01 s -0, 01 / 3, 12 = - 0, 003 (- 0, 3%) 3, 20 s 3, 20 -3, 12 = + 0, 08 s +0, 08 / 3, 12 = + 0, 026 (+ 2, 6%) 3, 15 s 3, 15 - 3, 12 = + 0, 03 s +0, 03 / 3, 12 = + 0, 010 (+ 1, 0%)

B) Significant Figures= Precision

Significant Figures= Precision n The significant figures in a measurement include all of the digits that are known, plus one last digit that is estimated.

Centimeters and Millimeters

Graduated Cylinder - Meniscus

B) International System of Units and Prefixes

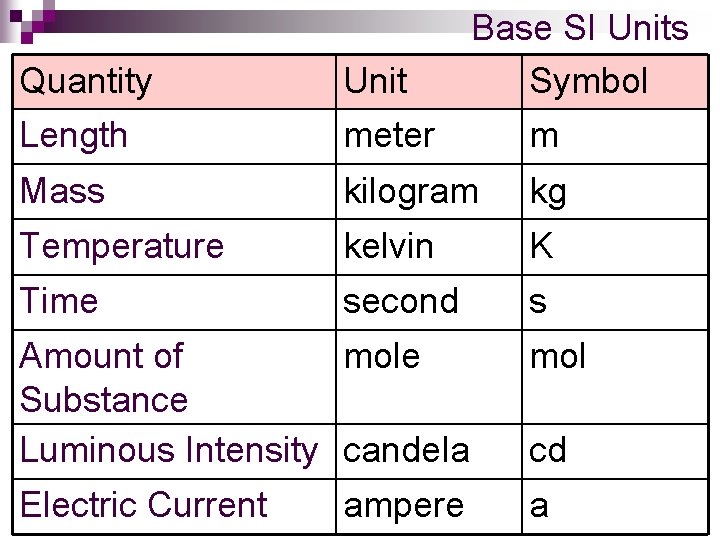
Quantity Unit Base SI Units Symbol Length meter m Mass kilogram kg Temperature kelvin K Time second s Amount of mole Substance Luminous Intensity candela mol Electric Current a ampere cd

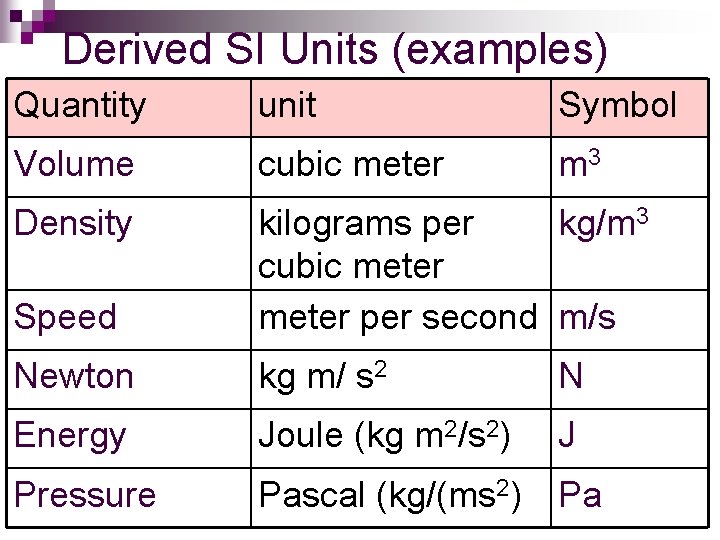
Derived SI Units (examples) Quantity unit Symbol Volume cubic meter m 3 Density Speed kilograms per kg/m 3 cubic meter per second m/s Newton kg m/ s 2 N Energy Joule (kg m 2/s 2) J Pressure Pascal (kg/(ms 2) Pa

Units for Volume m 3 cm 3 1 dm 3 = 1 L dm 3 1 cm 3= 1 m. L Liter

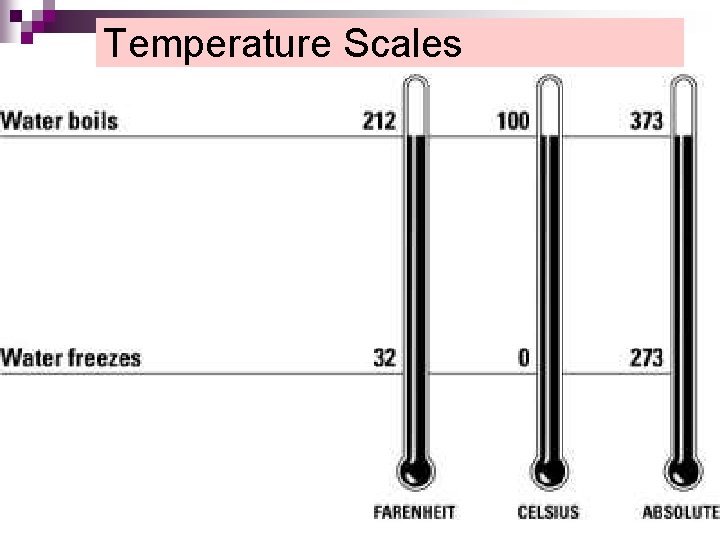
Temperature A measure of how hot or how cold an object is. SI Unit: the kelvin ( K ) n Note: not a degree n Absolute Zero= 0 K

Temperature Scales

Celsius and Kelvin K= o. C + 273

Farenheit and Celsius o. F= (1, 8 o. C ) +32

Unit for Weight 1 Newton 1 N= kg m/s 2

Units for Energy n Joule J n calorie 1 cal= 4, 184 J 1 cal = quantity of heat needed to raise the temp of 1 g of water by 1 o. C.

Note: 1 Cal = 1 kcal =1000 cal

SI Unit Prefixes Name gigamegakilodecicentimillimicronanopico- Symbol G M k d c m μ n p 109 106 103 10 -1 10 -2 10 -3 10 -6 10 -9 10 -12

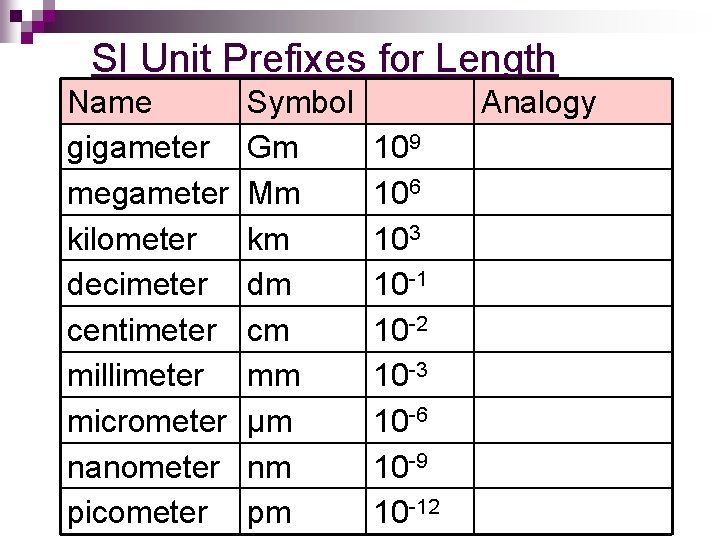
SI Unit Prefixes for Length Name gigameter megameter kilometer decimeter centimeter millimeter micrometer nanometer picometer Symbol Gm Mm km dm cm mm μm nm pm Analogy 109 106 103 10 -1 10 -2 10 -3 10 -6 10 -9 10 -12

C) Factor Label Method of Unit Conversion- Dimensional Analysis

Factor-Label Method n Example: Convert 5 km to m: NEW UNIT 5 km x 1000 m =5000 m km OLD UNIT

Convert 7000 m to km 7000 m x 1 km = 7 km 1000 m

Convert 2, 45 cs to s n 2, 45 cs x 1 s = 0, 0245 s 100 cs

Convert 55, 00 km/h to m/s 55, 00 km x 1000 m x 1 h___ = 15, 28 m/s h 1 km 3600 s