UNITI CRYSTALLOGRAPHY AND CRYSTAL STRUCTURES Space Lattice Unit

UNIT-I CRYSTALLOGRAPHY AND CRYSTAL STRUCTURES Space Lattice, Unit Cell, Lattice Parameters, Crystal Systems, Bravais Lattices, Miller Indices, Crystal Planes and Directions, Inter Planar Spacing of Orthogonal Crystal Systems, Atomic Radius, Coordination Number and Packing Factor of SC, BCC, FCC, and hcp Structures.

Introduction: Solids can be broadly classified into two categories based on the arrangement of atoms or molecules as crystalline and non crystalline (amorphous). In crystalline solids the atoms or molecules are arranged in a periodic manner in all three directions and further those are classified as mono (single) crystals and polycrystalline solids.

• • • Crystals which have different periodic arrangements in all the three directions exhibit varying physical properties with directions and they are called anisotropic substances. Ex: Al, Cu, Ag, Ge, Si, Diamond etc… Non crystalline substances are also called amorphous. In amorphous solids the atoms or molecules arranged randomly and which have no regular structure. They have no directional properties and therefore they are called as isotropic substances. Ex: Rubber, Glass, Wood, Plastic etc….

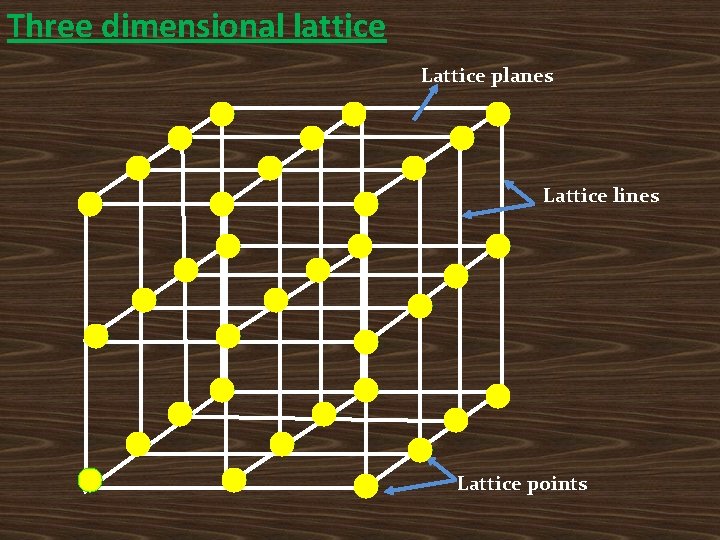
Crystallography: Study of the geometrical form and other physical properties of crystalline solids by using x-rays, neutron beams and electron beams. Crystallography is mainly used to determine the internal atomic arrangement in crystals, bonding and their strength. Lattice: The periodic arrangement of atoms in a crystal is called lattice. Lattice Point: which denote the position of atoms or molecules (Imaginary points). • Each lattice point in space may represent a single atom or group of atoms. • Ex: In Ge & Si, each lattice point is 1 atom. In Na. Cl, each lattice point is 1 Na. Cl molecule.

Space lattice: A space lattice is defined as an infinite array of points in three dimensions in which every point has an identical environment to that of every other point in the array. • P b a Where a and b are called the repeated translation vectors.

The position vector of any lattice point for two dimensional space lattice is The position vector of any lattice point for three dimensional space lattice is Where n 1, n 2& n 3 are the integers , a, b & c are the translational vectors on along the crystallography axes

Three dimensional lattice Lattice planes Lattice lines Lattice points

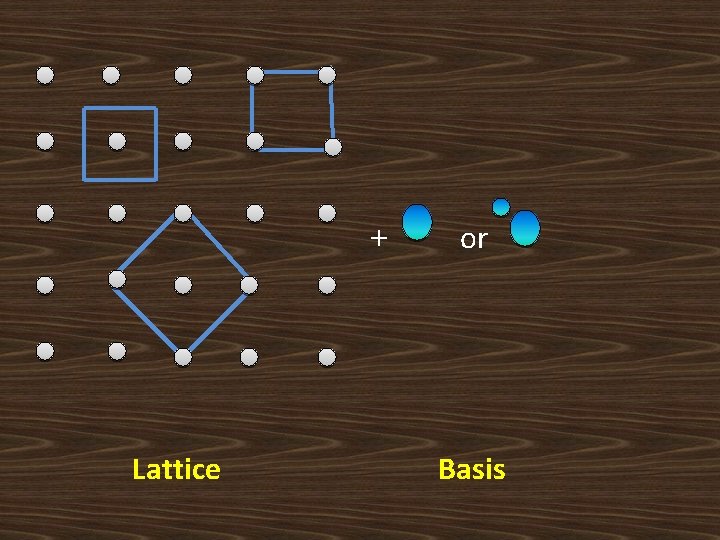
BASIS : A group of atoms or molecules identical in composition, arrangement or orientation is called the Basis. The basis provides the number of atoms per lattice point, their types and orientation. Lattice + basis = crystal structure

+ Lattice or Basis

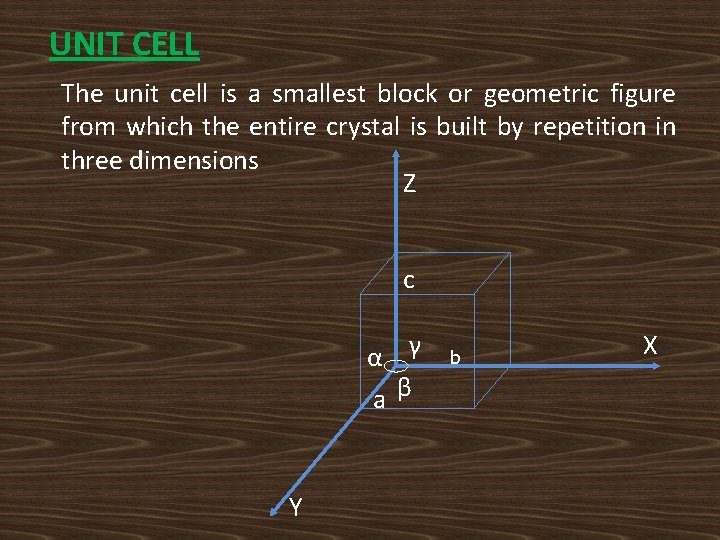
UNIT CELL: The unit cell is a smallest block or geometric figure from which the entire crystal is built by repetition in three dimensions Z c α γ aβ Y b X

CRYSTALLOGRAPHIC AXES: The lines drawn parallel to the lines of intersection of any three faces of the unit cell which do not lie inthe same plane are called crystallographic axes. PRIMITIVES: a, b and c are the dimensions of an unit cell and are known as Primitives. INTERFACIAL ANGLES: The angles between three crystallographic axes are known as Interfacial angles α , β and γ.

PRIMITIVE CELL: The unit cell is formed by primitives is called primitive cell. A primitive cell will have only one lattice point. LATTICE PARAMETERS: The primitives and interfacial angles are called lattice parameters. NOTE: i). Primitives decides the size of the unit cell. ii). Interfacial angles and primitives together decides the shape and size of the unit cell.

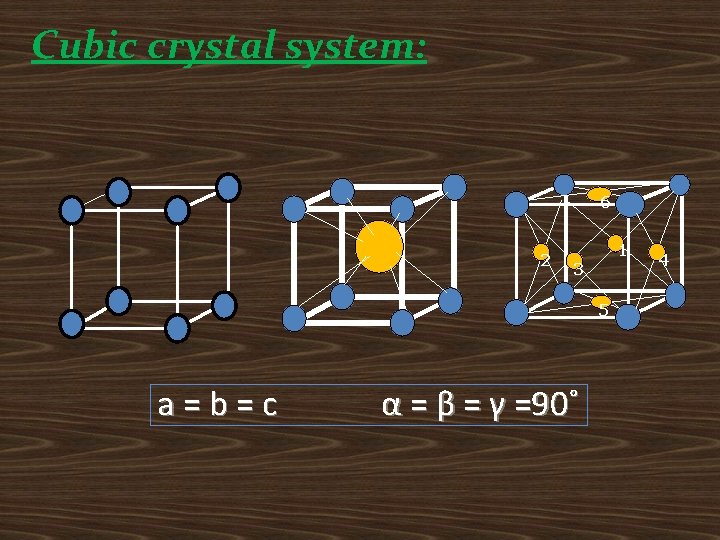
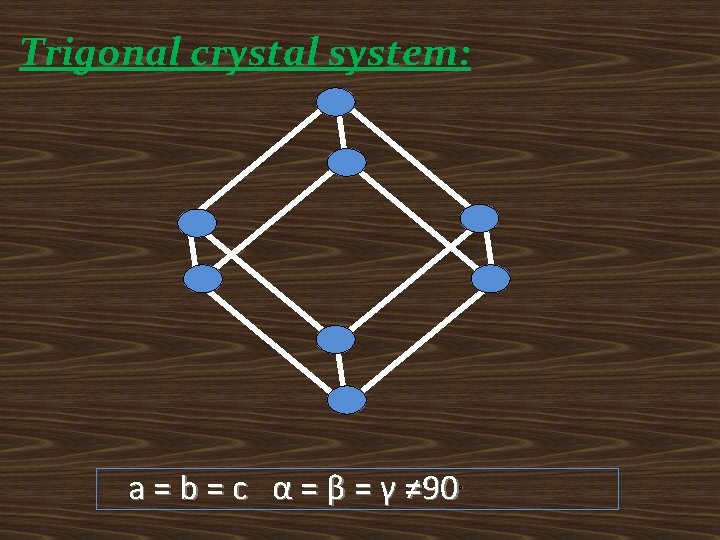
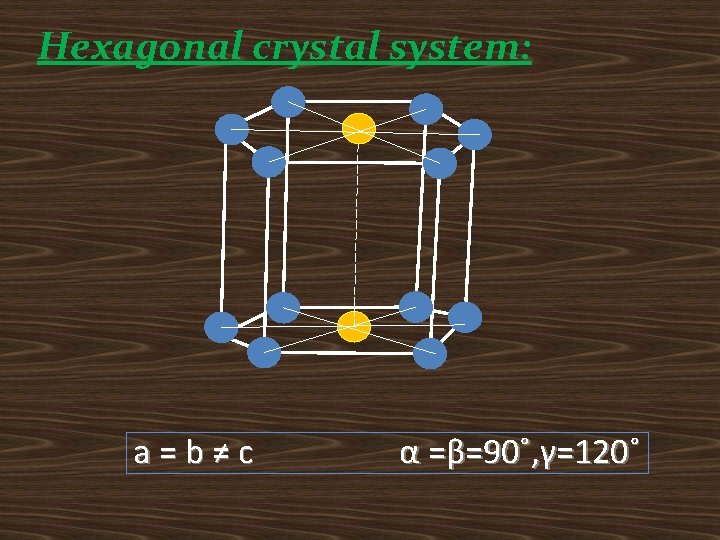
Crystal Systems: Crystals are classified into seven crystal systems on the basis of shape of the unit cell or lattice parameters in terms of lengths and the angle of inclination between them. The seven crystal systems are i). Cubic ii). Tetragonal iii). Orthorhombic iv). Monoclinic v). Triclinic vi). Trigonal (or) Rhombohedral vii). Hexagonal

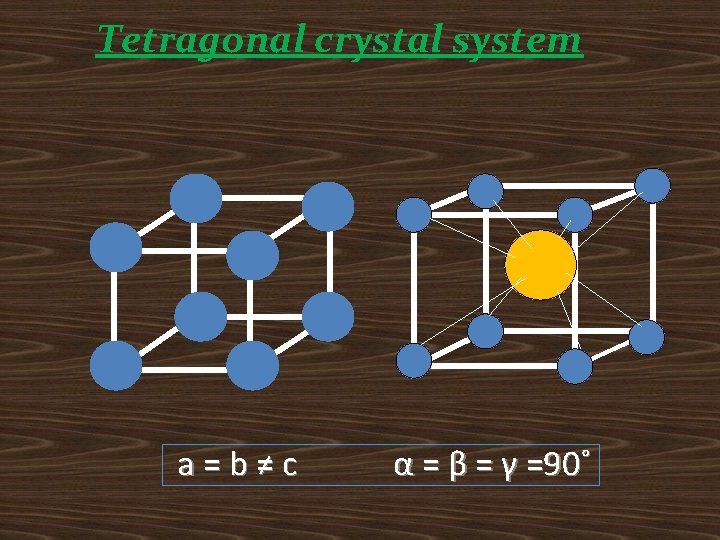
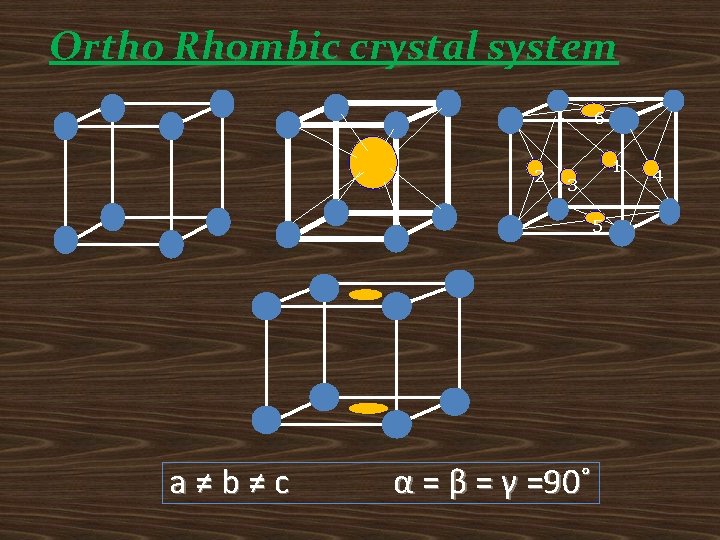
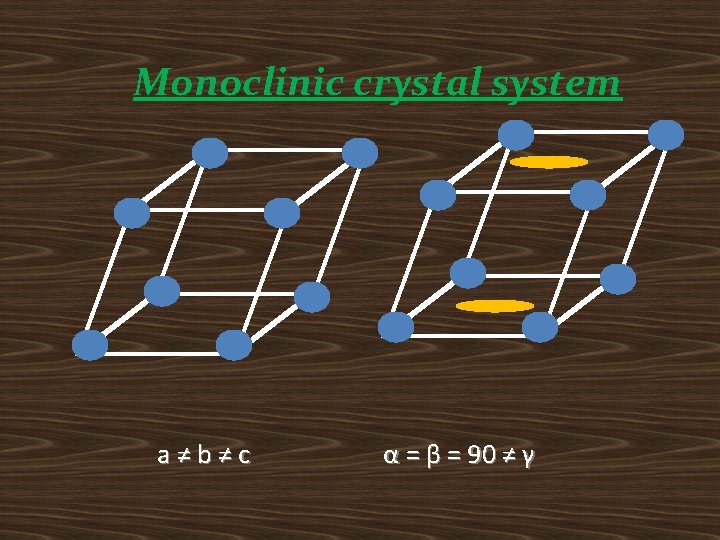
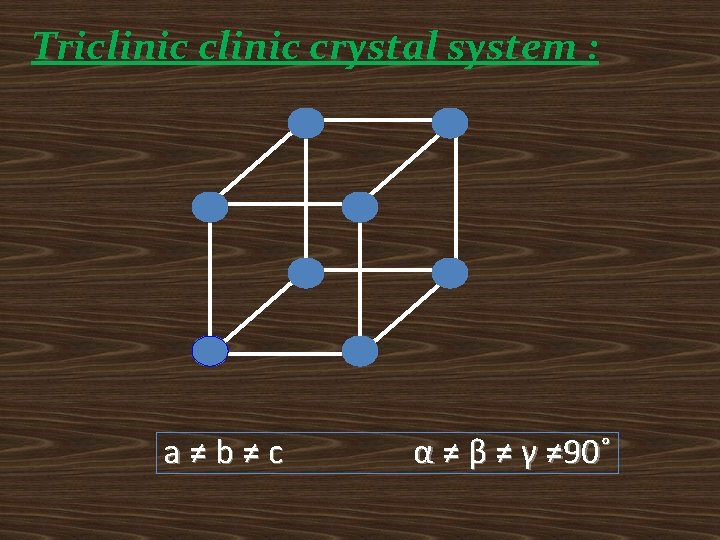
Crystal System Unit Vector Angles Examples Cubic a=b=c α = β = γ =90˚ Cu, Ag, Na, Po Tetragonal a=b≠c α = β = γ =90˚ Sn. O 2, Ti. O 2 Orthorhombic a≠b≠c α = β = γ =90˚ Ba. SO 4, Mg. SO 4 Monoclinic a≠b≠c α = β = 90 ≠γ Triclinic a ≠ b ≠c α ≠ β ≠ γ ≠ 90˚ u. SO 4 5 H 2 O Trigonal a=b=c α = β = γ ≠ 90˚ As, Bi, Sb, Calcite Hexgonal a=b≠c α =β=90˚, γ=120˚ Zn, Cd, Si. O 2 Ca. SO 4 2 H 2 O

BRAVAIS LATTICES: According to Bravais, there are only 14 distinguishable ways of arranging lattice points in a three dimensional space so that the environment looks the same from each point. The lattices are called Bravais lattices. The classification of Bravais lattices is based on the following crystal lattices. i). Primitive Lattice(P) ii). Body Centered Lattice(I) iii). Face Centered Lattice(F) And iv). Base Centered Lattice(C).

i). Primitive Lattice(P): Primitive Lattice structure has 8 lattice points at the eight corners of the unit cell and each point share with another 8 unit cells No. of lattice points in unit cell=(1/8)*8=1 lattice point/cell

i). Body Centered Lattice(I): Body Centered Lattice structure has 8 lattice points at the eight corners of the unit cell with addition of one center lattice point. Corner lattice point share with another 8 unit cells and center point is independent to other unit cells No. of lattice points in unit cell=(1/8)*8+1=2 lattice points/cell

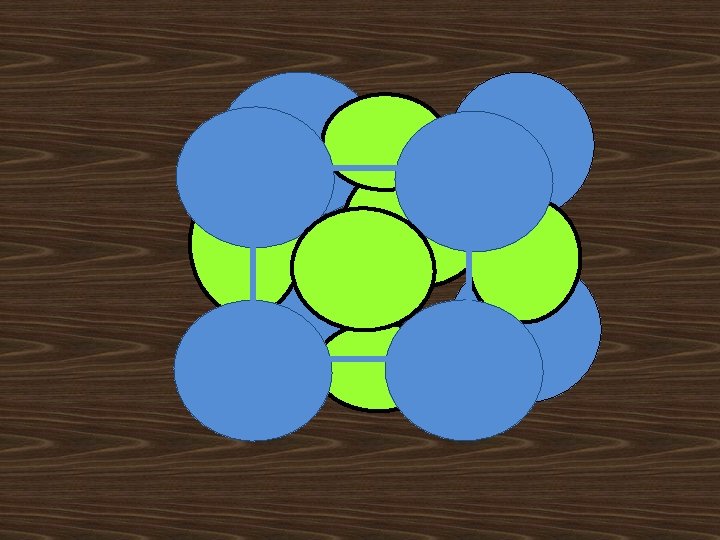
iii). Face Centered Lattice(F): 6 2 1 3 4 5 Face Centered Lattice structure has 8 lattice points at the eight corners of the unit cell with addition of these points six faces having 6 lattice points. Corner lattice point share with another 8 unit cells and face centered lattice point share with 2 unit cells No. of lattice points in unit cell=(1/8)*8+(1/2)*6=4 lattice points/cell

iv). Base Centered Lattice(F): Base Centered Lattice structure has 8 lattice points at the eight corners of the unit cell with addition of these points two bases having 2 lattice points. Corner lattice point share with another 8 unit cells and base centered lattice point share with 2 unit cells No. of lattice points in unit cell=(1/8)*8+(1/2)*2=2 lattice points/cell

CRYSTAL TYPE SYMBOLS BRAVAIS LATTICE • Cubic Simple Body Centered Face Centered • Tetragonal Simple Body Centered P I • Orthorhombic Simple Base Centered Body Centered Face Centered P C I F • Monoclinic Simple Base Centered P C • Triclinic Simple P • Trigonal Simple P • Hexgonal Simple P 7 P+3 I+2 F+2 C = 14 Thus the total number of Bravais Lattices are 14 P I F

Cubic crystal system: 6 2 1 3 5 a=b=c α = β = γ =90˚ 4

Tetragonal crystal system a=b≠c α = β = γ =90˚

Ortho Rhombic crystal system 6 2 1 3 5 a≠b≠c α = β = γ =90˚ 4

Monoclinic crystal system a≠b≠c α = β = 90 ≠ γ

Triclinic crystal system : a≠b≠c α ≠ β ≠ γ ≠ 90˚

Trigonal crystal system: a = b = c α = β = γ ≠ 90˚

Hexagonal crystal system: a=b≠c α =β=90˚, γ=120˚

NEAREST NEIGHBOR DISTANCE(2 r): The distance between the centers of two nearest neighboring atoms is called nearest neighbor distance. r r 2 r ATOMIC RADIUS(r ): Atomic radius is defined as half of the distance between the nearest neighboring atoms in an unit cell of a crystal atomic radius= r

CO-ORDINATION NUMBER: Co-ordination number is defined as the number of equidistance nearest neighbors that an atom has in its unit cell. Its signifies the tightness of packing of atoms in the crystal. More closely packed structure has greater coordination number Ex: Simple cubic=6, Body Centered=8, Face centered=12

ATOMIC PACKING FACTOR: Atomic packing factor is the ratio of volume occupied by the atoms in a unit cell to the total volume of the unit cell. It is also called packing fraction. Atomic Packing factor = volume occupied by the atoms in a unit cell / Total volume of a unit cell. v The packing factor varies from 0. 34 to 0. 74 for different crystal structures v High value indicates that very closely packed and low value Indicates loosely packed structure.

Void space: Void space in the unit cell is the vacant space left or unutilized space in unit cell and more commonly known as interstitial space. Void space = ( 1 -APF )X 100

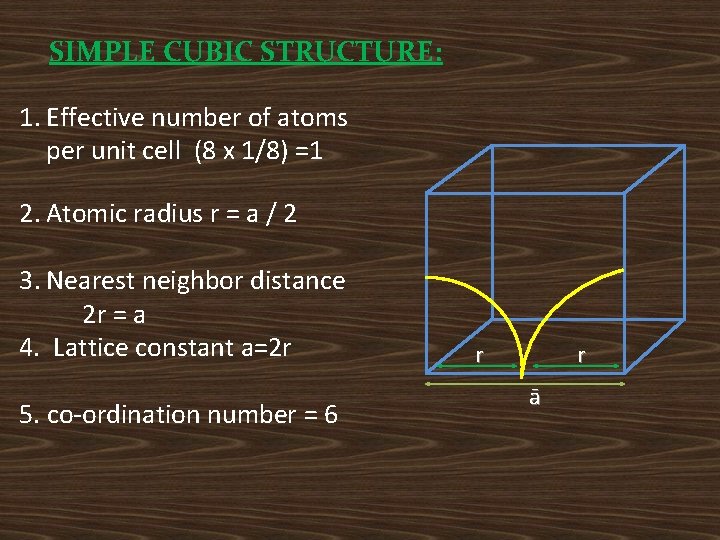
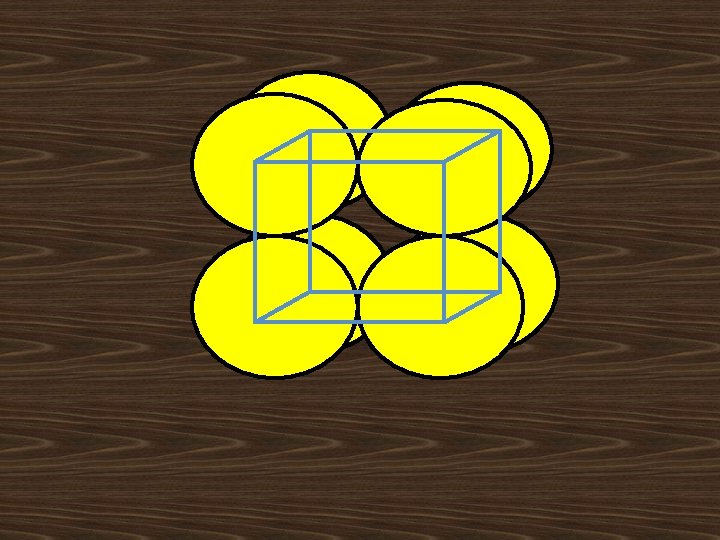
SIMPLE CUBIC STRUCTURE: 1. Effective number of atoms per unit cell (8 x 1/8) =1 2. Atomic radius r = a / 2 3. Nearest neighbor distance 2 r = a 4. Lattice constant a=2 r 5. co-ordination number = 6 r r ā

6. Atomic packing factor 7. Void space = (1 -APF) X 100 = (1 -0. 52)X 100 =48% Ex: Polonium.

BCC STRUCURE: 1. Effective number of atoms per unit cell (8 x 1/8) + I =2 D 2. Atomic radius r = √ 3 a /4 3. Nearest neighbor distance 2 r =√ 3 a/2 4. Lattice constant a=4 r/√ 3 5. Co-ordination number = 8 4 r ā C √ 2ā A ā B ā

6. Atomic packing factor 7. Void space = (1 -APF) x 100 = (1 -0. 68) x 100 = 32% • Ex: Na, lithium and Chromium.

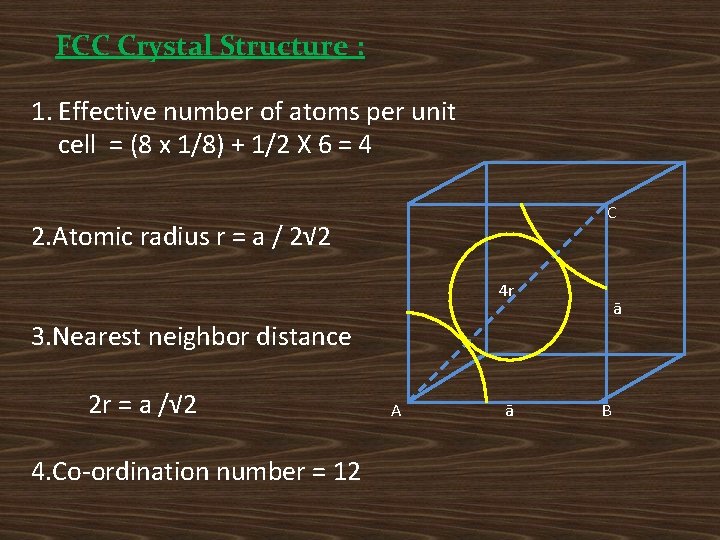
FCC Crystal Structure : 1. Effective number of atoms per unit cell = (8 x 1/8) + 1/2 X 6 = 4 C 2. Atomic radius r = a / 2√ 2 4 r ā 3. Nearest neighbor distance 2 r = a /√ 2 4. Co-ordination number = 12 A ā B

5. Atomic packing factor 6. Void space = (1 -APF) X 100 = (1 -0. 74) X 100 = 26% Ex: Cupper , Aluminum, Silver and Led

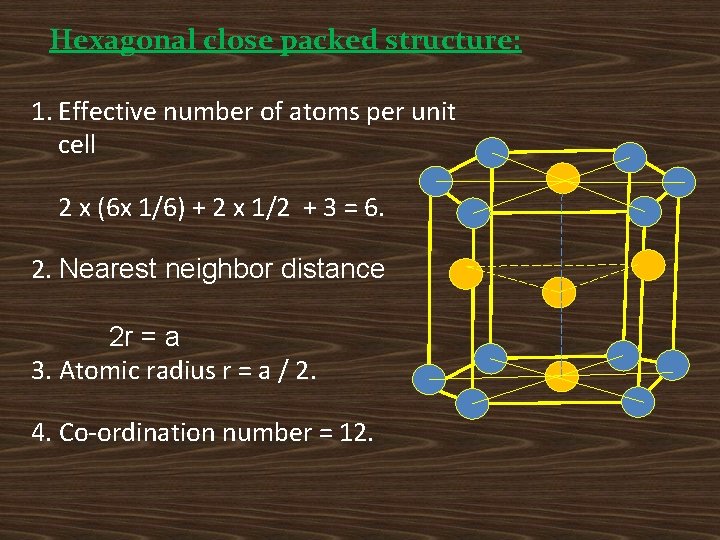
Hexagonal close packed structure: 1. Effective number of atoms per unit cell 2 x (6 x 1/6) + 2 x 1/2 + 3 = 6. 2. Nearest neighbor distance 2 r = a 3. Atomic radius r = a / 2. 4. Co-ordination number = 12.

5. Volume of the HCP unit cell: The volume of the unit cell determined by computing the area of the base of the unit cell and then by multiplying it by the unit cell height. Volume = (Area of the hexagon) x (height of the cell) Area of the hexagon: o A If c is the height of the unit cell 60° O B

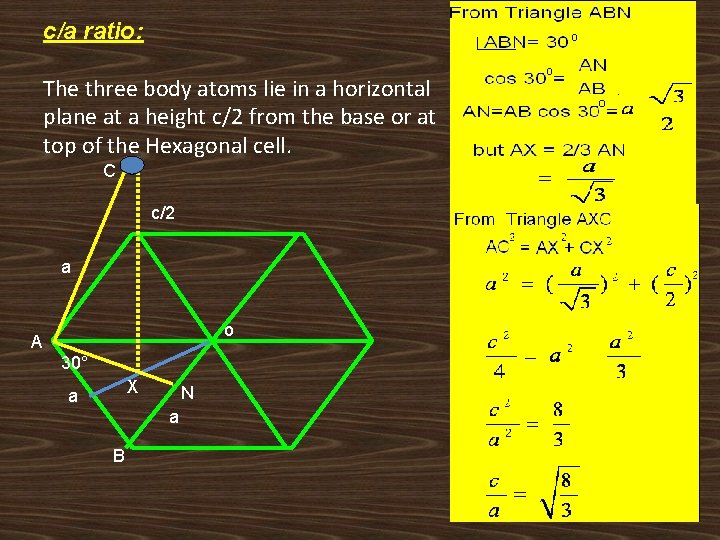
c/a ratio: The three body atoms lie in a horizontal plane at a height c/2 from the base or at top of the Hexagonal cell. C c/2 a o A 30° X a N a B

6. Atomic packing factor 7. Void space = (1 -APF) x 100 = (1 -0. 74) x 100 = 26% Ex: Mg, Cd and Zn.

Directions and Planes in Crystals: In crystals atoms are regularly arranged in space such that environment about any atom is same. There exists some directions and planes which contains large concentration of atoms. For understanding crystallography, the concept of directions and planes play an important role. Directions : In crystal analysis, it is essential to indicate certain directions inside the crystal and which is a line joining any two points of the lattice.

Two dimensional crystal directions representation: y A [1 2 ] B[1 1 ] C[3 2 ] D[3 1 ] O x Let ‘o’ be the origin of the pattern. Consider the directions OA, OB, OC & OD. The direction is described by giving the first integer point (x, y) through which the line passes.

• The line OA is passing through the first lattice point at x=1 & y=2. Therefore, the direction OA is given by [1 2]. • A convention square brackets are used to represent directions. Three dimensional crystal directions representation: z P[u v w] Suppose to indicate the direction ‘OP’ as shown in figure. Consider x. y & z are the crystallography axes. c o a x ua wc b vb y

• If a, b and c represent unit translational vectors along x, y and z directions, then moving ‘u’ times ‘a’ along x-axis, ‘v’ times ‘b’ along y-axis and ‘w’ times ‘c’ along z-axis, we can reach ‘P’. • If u, v and w are the smallest integers, the direction ‘OP’ is indicated by [u v w]. z [001] Ex: Some important directions in a cubic crystal [011] [111] [000] x [100] [010] [110] y

Some important directions in cubic crystal: • Square brackets [ ] are used to indicate the directions • The digits in a square brackets indicate the indices of that direction. • A negative index is indicated by a ‘bar’ over the digit. • Ex: for positive x-axis→[ 100 ] • for negative x-axis→[ 100 ]

Crystal planes: A crystal is made up of a large number of parallel equidistant planes passing through lattice points are called Lattice planes or crystal planes. ØThe perpendicular distance between adjacent planes is called inter planar spacing. ØThe distance between parallel planes of any these sets is called the lattice spacing.

Miller indices: The Miller Indices are three smallest possible integers (h k l), which have the same ratio as the reciprocals of the intercepts of the crystal plane having on the three crystallographic axes. • These indices are used to indicate the different sets of parallel planes in a crystal.

Procedure for finding Miller indices: z C r A x o p q B y

Choose system of three coordinate axes x, y & z i. e. , crystallographic axes Determine the intercepts p, q & r of the required plane ‘ABC’ on these axes i. e. , OA = p, OB = q & OC = r. Take ratio of reciprocals of the Intercepts i. e. , 1/p: 1/q: 1/r. Convert these reciprocals into integers by multiplying each one of them with their L. C. M. Enclose these integers in smaller parenthesis i. e. , Miller indices (h k l) of the crystal.

Important features of miller indices: • When a plane is parallel to any axis, the intercept of the plane on that axis is infinity. Hence its miller index for that axis is zero. • When the intercept of a plane on any axis is negative a bar is put on the corresponding miller index. • All equally spaced parallel planes have the same index number (h k l). • If a plane passes through origin, it is defined in terms of a parallel plane having non-zero intercept. • If a normal is drawn to a plane (h k l), the direction of the normal is [h k l].

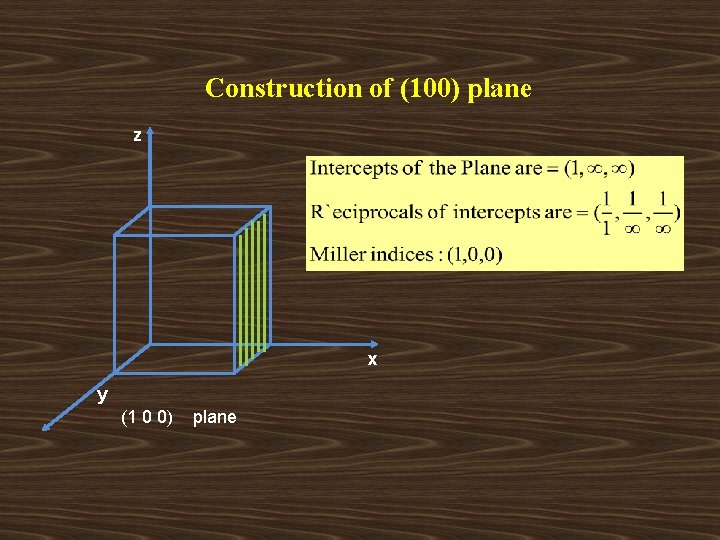
Construction of (100) plane z x y (1 0 0) plane

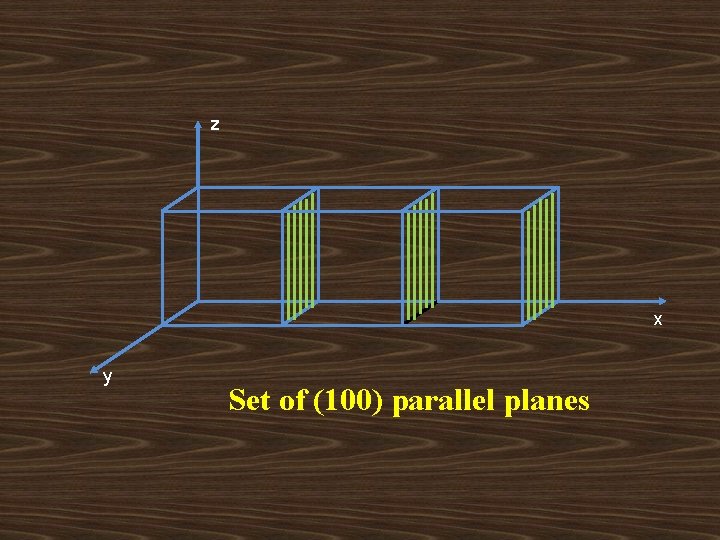
z x y Set of (100) parallel planes

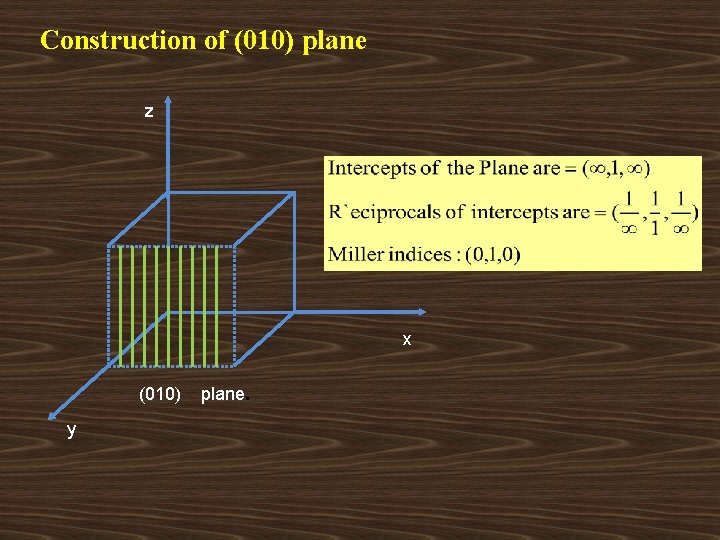
Construction of (010) plane z x (010) y plane.

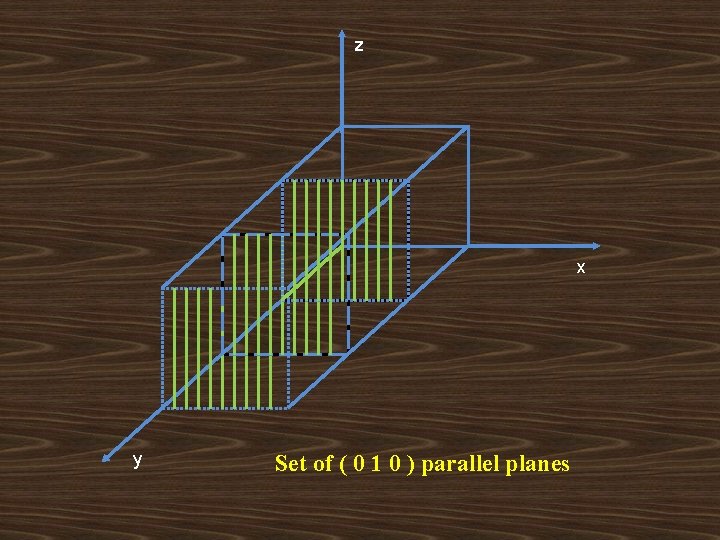
z x y Set of ( 0 1 0 ) parallel planes

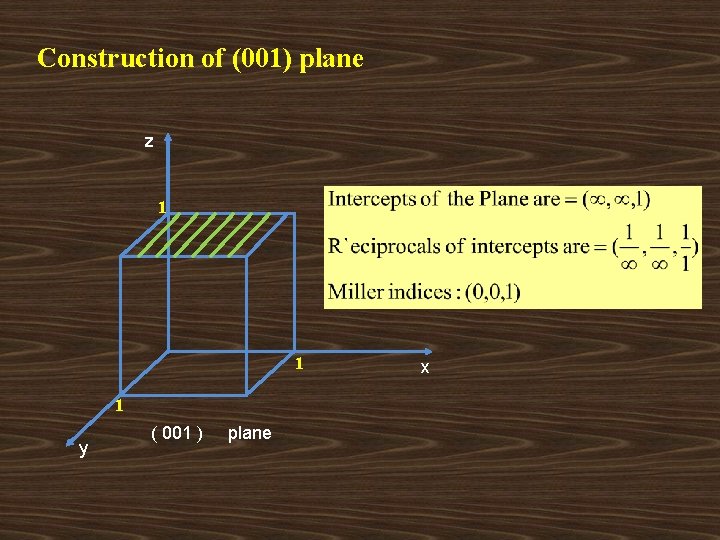
Construction of (001) plane z 1 1 1 y ( 001 ) plane x

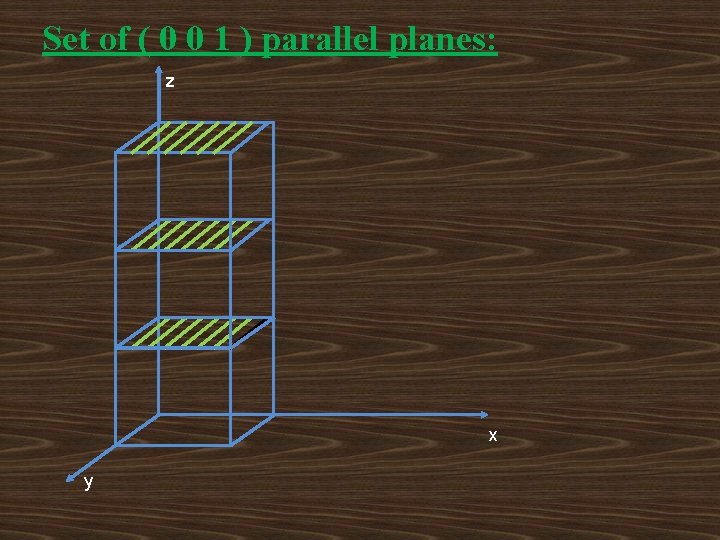
Set of ( 0 0 1 ) parallel planes: z x y

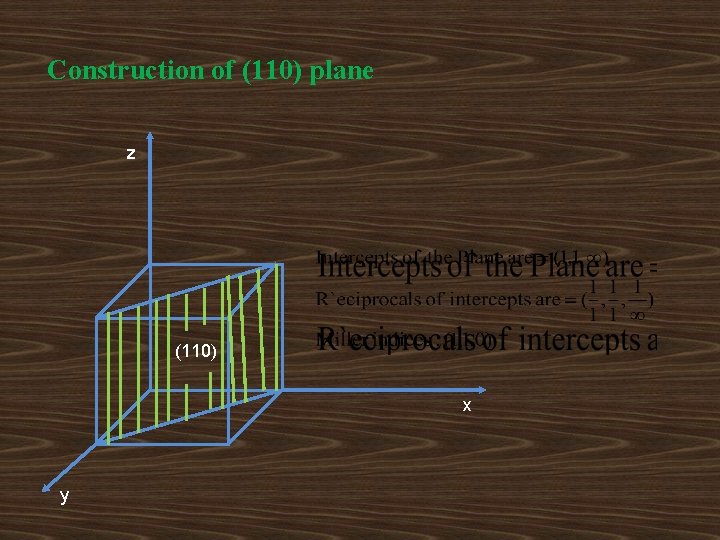
Construction of (110) plane z (110) x y

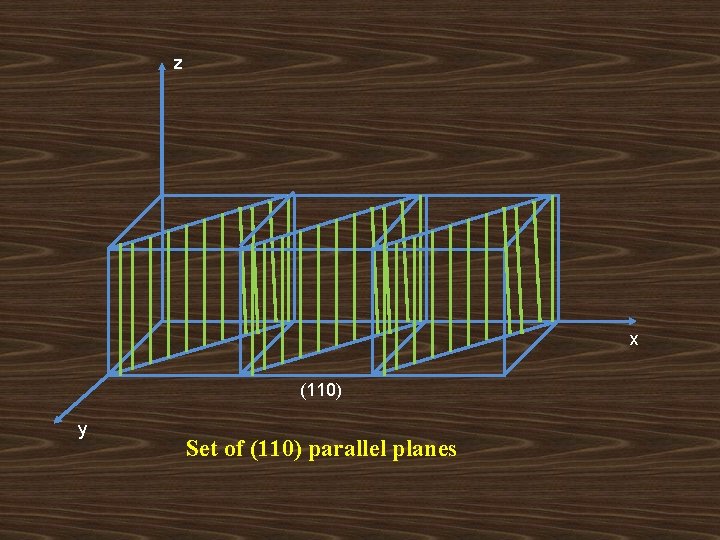
z x (110) y Set of (110) parallel planes

Construction of ( ī 0 0) Planes z x y

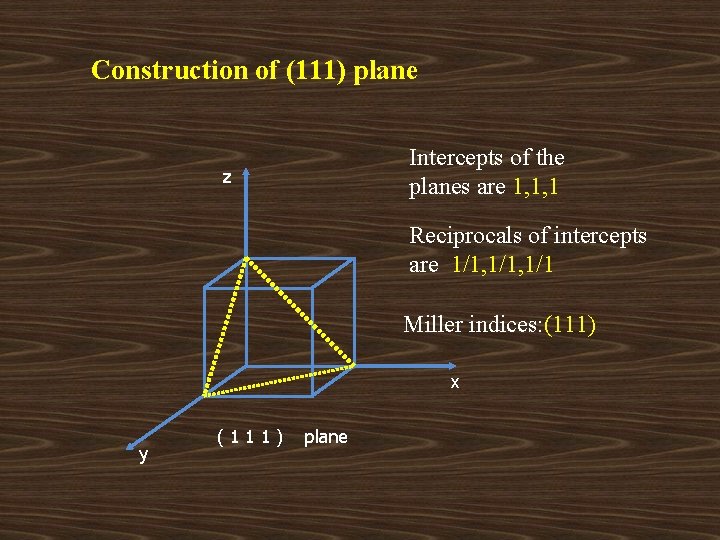
Construction of (111) plane Intercepts of the planes are 1, 1, 1 z Reciprocals of intercepts are 1/1, 1/1 Miller indices: (111) x y (111) plane

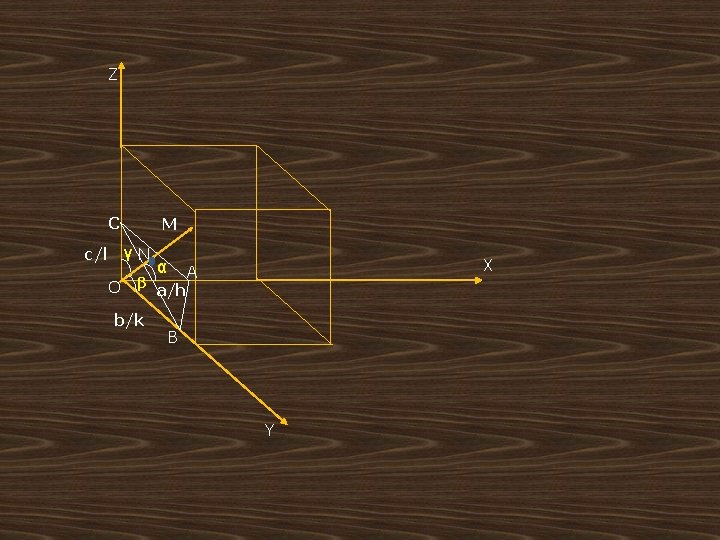
Inter planner spacing of orthogonal crystal system: (in 3 dimensions) • • ‘The distance ‘d’ between a series of planes in a crystal is known as the ‘d’ spacing or inter planar spacing’. Let ( h , k, l ) be the miller indices of the plane ABC. Let ON=d be a normal to the plane passing through the origin ‘ 0’. Let this ON make angles α, β and γ with x, y and z axes respectively. Imagine the reference plane passing through the origin “o” and the next plane cutting the intercepts a/h, b/k and c/l on x, y and z axes.

Z C M γN c/l O β b/k α a/h X A B Y

• Let the direction cosines of ON be cosα, cosβ & cosγ • but law of direction cosines

• Let OM be the perpendicular distance of the next plane from the origin and its intercepts 2 a/h, 2 b/k & 2 c/l.

• Therefore, the spacing between the adjacent planes dhkl = OM-ON Note: The inter planar spacing of Simple Cubic Structure a=b=c

THANK U