Unitat 2 Les forces i els seus efectes

Unitat 2: Les forces i els seus efectes 1. La natura de les forces 2. Equilibri de forces 3. Forces i deformacions 4. La pressió 5. Esquema de la unitat Imma Ros Mariona Bassedas Sònia Conesa Marta Segura

1. La natura de les forces Una força o interacció és tota aquella causa que fa que l’estat de moviment d’un cos canviï –és a dir, que experimenti una acceleració– o bé que es modifiqui la forma d’un cos –és a dir, que deformi un cos que resta immòbil. En aquesta unitat coneixerem les lleis de l’estàtica, que són les que estudien les forces que actuen sobre un cos en equilibri. Veurem com diferents forces poden modificar la forma d’un cos i com es pot aconseguir l’equilibri de les forces –de manera que la força resultant sigui zero– en estructures complexes. Les aplicacions de l’estàtica són molt nombroses, sobretot en arquitectura i enginyeria, àmbits en els quals són necessaris càlculs acurats d’equilibri de forces per construir edificis i estructures –com ponts o viaductes– que puguin resistir bé tot tipus de tensions. Gràcies als coneixements sobre estàtica, es poden construir ponts que travessen el mar, túnels per sota dels oceans i edificis de gran alçària. Índex

1. La natura de les forces 1. 1. Característiques de les forces En primer lloc estudiarem les característiques de la magnitud física que anomenem força. No totes les forces produeixen els mateixos efectes. El resultat d’aplicar una força sobre un cos depèn de la intensitat, de la direcció i del sentit en què s’exerceix la força, i del seu punt d’aplicació. És per aquesta raó que les forces les representem mitjançant vectors. Les unitats de força en el Sistema Internacional són els newtons, que representem amb la lletra N. El newton es defineix com 1 N = 1 kg · m/s 2. Índex

1. La natura de les forces 1. 1. Característiques de les forces Els components de tot vector són els següents: a) Mòdul: valor de la intensitat de la força. Com més gran sigui la intensitat d’una força, més llarga serà la longitud del vector que la representa. b) Direcció: recta sobre la qual s’aplica la força. c) Sentit: cap on es dirigeix la força aplicada. Cada direcció té dos possibles sentits, que es representen amb la punta d’una fletxa. d) Punt d’aplicació: punt de l’objecte sobre el qual s’aplica la força. Per exemple, quan colpegem una pilota de tennis amb una raqueta, el punt d’aplicació de la força que fa la raqueta sobre la pilota és el punt de contacte entre la raqueta i la pilota. Índex

1. La natura de les forces 1. 2. Tipus de forces Existeixen molts tipus diferents de forces a la natura, que podem classificar segons diversos factors: a) Segons l’agent responsable de la força: • Forces externes (com la d’un futbolista que colpeja una pilota). • Forces internes (com la que proporciona el motor d’un cotxe). b) Segons la distància entre l’agent que causa la força i l’objecte: • Forces de contacte (la que fem en empènyer un objecte). Terra al voltant • Forces a distància (com la força de la gravetat, que fa girar la del Sol). c) Segons els paràmetres dels quals depèn la força entre dos objectes: • Forces que depenen de la distància (com la força d’una molla). • Forces que depenen de la velocitat (com la força de fregament amb l’aire). Índex

1. La natura de les forces 1. 2. Tipus de forces Aquest conjunt de forces tenen un ventall molt ampli d’intensitats i es poden reduir a quatre interaccions fonamentals: la força gravitatòria, la força electromagnètica i les forces nuclears forta i feble, que difereixen entre si en la intensitat, en l’abast que tenen i en els cossos als quals afecten: La força nuclear forta és la interacció més intensa de totes, però no la percebem en el dia a dia perquè només actua en l’interior del nucli atòmic. És la força responsable de mantenir units els nuclis atòmics i, per tant, fa possible l’existència de la matèria. També els efectes de la força nuclear feble són molt rellevants: és la responsable de la desintegració dels nuclis atòmics i, per tant, de molts processos radioactius. Índex

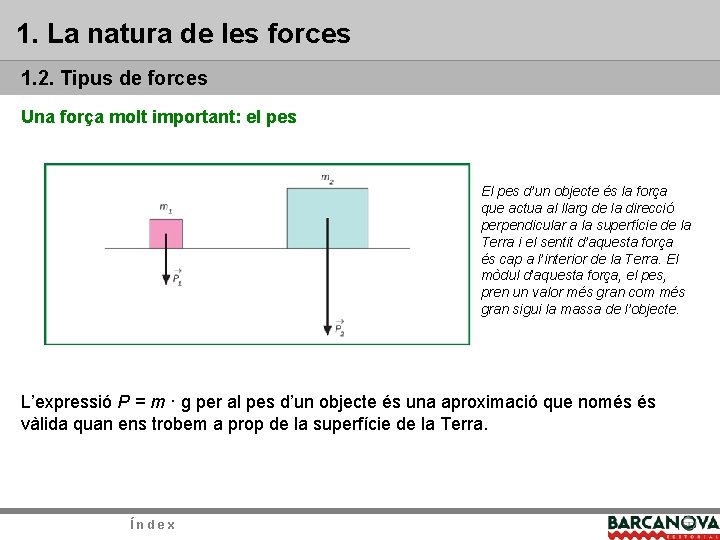
1. La natura de les forces 1. 2. Tipus de forces Una força molt important: el pes Quan deixem caure un cos sota l’acció de la força de la gravetat de la Terra, es troba en situació de caiguda lliure i experimenta una acceleració de g = 9, 8 m/s 2, anomenada acceleració de la gravetat. Aquesta acceleració és deguda als efectes de la força de la gravetat a prop de la superfície terrestre. A aquesta força l’anomenarem pes d’un objecte: el pes d’un cos de massa m és la força amb la qual el cos és atret cap a la superfície terrestre a causa dels efectes de la gravetat terrestre. L’expressió del pes és P = m · g, en què m és la massa del cos. Cal tenir en compte que el pes, com totes les forces, és una magnitud vectorial. El mòdul del pes és proporcional a la massa de l’objecte; per tant, com més massa tingui un objecte, més gran serà el seu pes. Índex

1. La natura de les forces 1. 2. Tipus de forces Una força molt important: el pes El pes d’un objecte és la força que actua al llarg de la direcció perpendicular a la superfície de la Terra i el sentit d’aquesta força és cap a l’interior de la Terra. El mòdul d’aquesta força, el pes, pren un valor més gran com més gran sigui la massa de l’objecte. L’expressió P = m · g per al pes d’un objecte és una aproximació que només és vàlida quan ens trobem a prop de la superfície de la Terra. Índex

1. La natura de les forces 1. 3. Composició de forces Quan diferents forces actuen sobre un cos, podem sumar-les per obtenir la força resultant, que és la força que té un efecte igual a la suma de totes les forces que actuen simultàniament sobre aquest cos. El càlcul de la força resultant d’un conjunt de forces que actua sobre un cos s’anomena composició de forces. Considerarem dos casos diferents de composició de forces: composició de forces concurrents i composició de forces paral·leles. Composició de forces concurrents Les forces concurrents són les que actuen sobre el mateix punt, és a dir, les que s’apliquen sobre el punt on es tallen dues rectes. Estudiarem la manera de determinar la força resultant depenent de la direcció i el sentit de les forces components, que són les forces que intervenen sobre el cos. Índex

1. La natura de les forces 1. 3. Composició de forces concurrents A l’hora de calcular la força resultant de dues forces que tenen la mateixa direcció, ens podem trobar les dues situacions següents: de la sentit la a) Si les dues forces tenen la mateixa direcció i el mateix sentit, el mòdul força resultant és la suma de les dues forces: FR = F 1 + F 2. La direcció i el de la força resultant seran els mateixos que els de les forces components. b) Si les forces tenen la mateixa direcció però sentit contrari, el mòdul de força resultant és la resta de les dues forces: FR = F 1 - F 2. La direcció és la mateixa que la de les forces components i el sentit és el de la força de més intensitat. La força resultant de dues forces d’igual magnitud i direcció, però de sentits oposats, que actuen de manera simultània sobre un cos, és 0. Índex

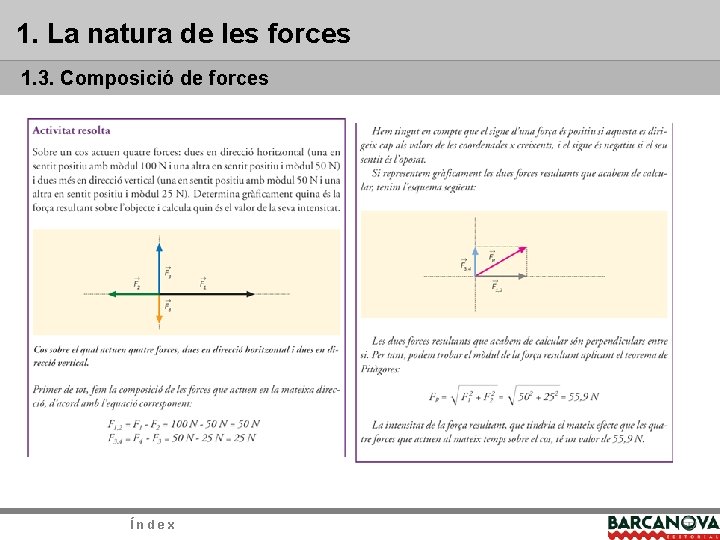
1. La natura de les forces 1. 3. Composició de forces concurrents La força resultant de dues forces concurrents de direccions perpendiculars correspon a la hipotenusa d’un triangle rectangle, els catets del qual són les dues forces que actuen sobre el cos; per tant, determinarem el mòdul de la força resultant mitjançant el teorema de Pitàgores: el quadrat de la hipotenusa és igual a la suma dels quadrats dels catets. D’aquesta manera la força resultant és la següent: Força resultant entre dues forces perpendiculars. El mòdul de la força resultant es pot determinar fent servir el teorema de Pitàgores sobre els triangles rectangles. Índex

1. La natura de les forces 1. 3. Composició de forces Índex

1. La natura de les forces 1. 3. Composició de forces Índex

1. La natura de les forces 1. 3. Composició de forces concurrents El càlcul de la força resultant de dues forces concurrents de direccions diferents el podem fer mitjançant la regla del paral·lelogram: per l’extrem de cada vector tracem una recta paral·lela a l’altre vector i assenyalem el punt d’intersecció. L’extrem de la força resultant és el punt d’intersecció de les dues rectes i el punt d’aplicació és el mateix que el de les forces components. La direcció i la intensitat de la força resultant queda determinada per la diagonal del paral·lelogram. Índex

1. La natura de les forces 1. 3. Composició de forces paral·leles Anem a veure com podem determinar la força resultant de forces paral·leles, és a dir, que tenen direccions paral·leles i que, per tant, actuen en diferents punts. Distingirem dos casos: les forces paral·leles del mateix sentit i les forces paral·leles de sentit contrari. En el cas de forces paral·leles del mateix sentit, la intensitat de la força resultant és la suma de les dues forces components: FR = F 1 + F 2 La direcció és la mateixa que en les forces components i el sentit també. El punt d’aplicació de la força resultant el determinarem mitjançant la relació següent: d 1 · F 1 = d 2 · F 2 d 1+ d 2 correspon a la distància entre els Índex punts d’aplicació de les forces.

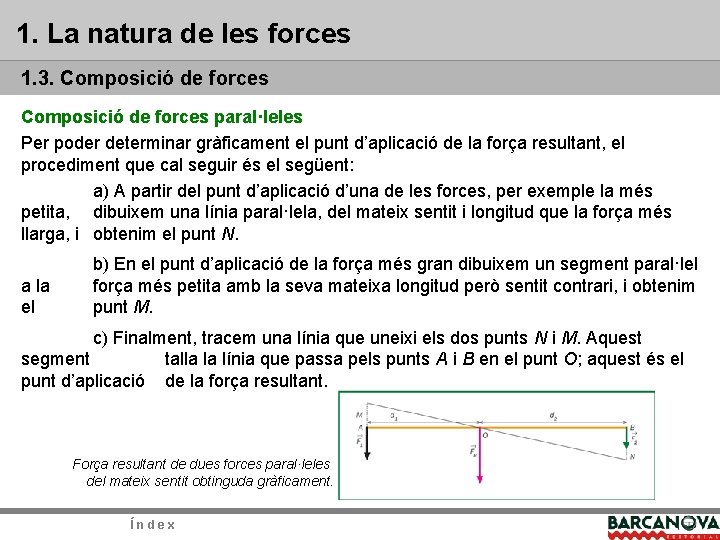
1. La natura de les forces 1. 3. Composició de forces paral·leles Per poder determinar gràficament el punt d’aplicació de la força resultant, el procediment que cal seguir és el següent: a) A partir del punt d’aplicació d’una de les forces, per exemple la més petita, dibuixem una línia paral·lela, del mateix sentit i longitud que la força més llarga, i obtenim el punt N. a la el b) En el punt d’aplicació de la força més gran dibuixem un segment paral·lel força més petita amb la seva mateixa longitud però sentit contrari, i obtenim punt M. c) Finalment, tracem una línia que uneixi els dos punts N i M. Aquest segment talla la línia que passa pels punts A i B en el punt O; aquest és el punt d’aplicació de la força resultant. Força resultant de dues forces paral·leles del mateix sentit obtinguda gràficament. Índex

1. La natura de les forces 1. 3. Composició de forces paral·leles Índex

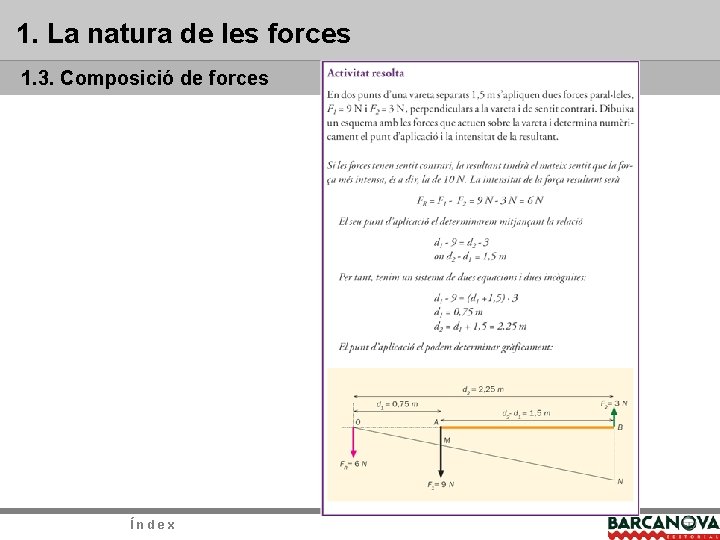
1. La natura de les forces 1. 3. Composició de forces paral·leles Quan es tracta de forces paral·leles de sentit contrari, la intensitat de la força resultant és la resta de les dues forces components, és a dir, FR = F 1 - F 2. La direcció és la mateixa que les forces components i el sentit de la resultant és el de la força de valor més alt. Podem calcular numèricament el punt d’aplicació de la resultant mitjançant l’expressió d 1 - F 1 = d 2 - F 2, en què d 2 - d 1 és la distància entre els punts d’aplicació de les forces. Per a aquest cas també podem determinar gràficament el punt d’aplicació de la resultant, seguint els mateixos passos que en el cas anterior. Força resultant de dues forces paral·leles de sentit contrari obtinguda gràficament. Índex

1. La natura de les forces 1. 3. Composició de forces Índex

2. Equilibri de forces Quan la força resultant que actua sobre un cos és zero, diem que ens trobem en una situació d’equilibri de forces, on els efectes de totes les forces que actuen sobre un cos es cancel·len entre si. Qualsevol estructura, com un pont o un edifici, es troba en situació d’equilibri de forces quan la força total sobre cada element d’aquesta estructura és zero. També podem dir que aquest objecte es troba en equilibri estàtic. La determinació de les forces que actuen sobre un cos en equilibri estàtic té moltes aplicacions pràctiques, sobretot en enginyeria. Per exemple, si es vol construir un pont que no caigui, s’han de conèixer les forces que actuaran sobre cada una de les seves parts per construir-les amb elements suficientment resistents. El viaducte de Millau, al departament francès d’Avairon, és una de les principals obres arquitectòniques de les darreres dècades. Índex

2. Equilibri de forces Segons la posició d’un cos, es poden distingir tres classes d’equilibri: l’equilibri estable, l’equilibri inestable i l’equilibri indiferent. seva • Un cos està en equilibri estable quan, si se’l desplaça lleugerament de la posició d’equilibri, hi torna així que se’l deixa anar. seva • Un cos està en equilibri inestable quan, si se’l desvia lleugerament de la posició d’equilibri, cau. • Un cos es troba en equilibri indiferent quan, si se’l desvia lleugerament de la seva posició d’equilibri, adopta una altra posició d’equilibri similar a l’anterior. Índex

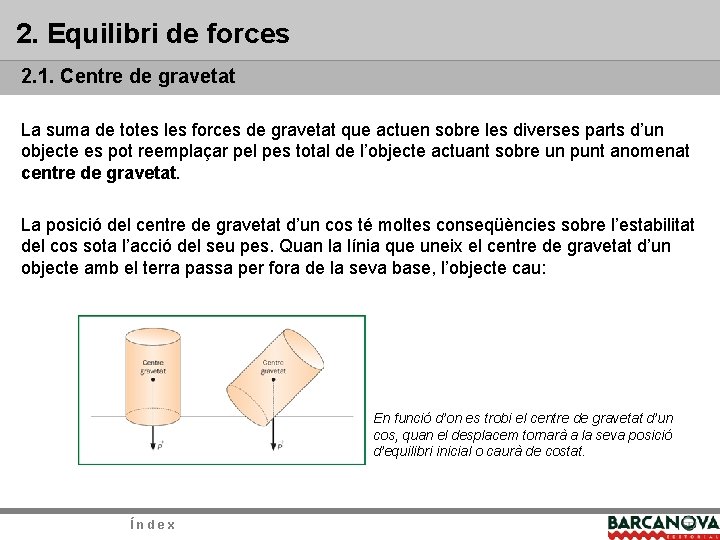
2. Equilibri de forces 2. 1. Centre de gravetat La suma de totes les forces de gravetat que actuen sobre les diverses parts d’un objecte es pot reemplaçar pel pes total de l’objecte actuant sobre un punt anomenat centre de gravetat. La posició del centre de gravetat d’un cos té moltes conseqüències sobre l’estabilitat del cos sota l’acció del seu pes. Quan la línia que uneix el centre de gravetat d’un objecte amb el terra passa per fora de la seva base, l’objecte cau: En funció d’on es trobi el centre de gravetat d’un cos, quan el desplacem tornarà a la seva posició d’equilibri inicial o caurà de costat. Índex

2. Equilibri de forces 2. 1. Centre de gravetat En els cossos regulars, com per exemple un rectangle, un cilindre o una esfera, el centre de gravetat coincideix aproximadament amb el centre geomètric. Per exemple, en un rectangle, el centre de gravetat es troba en el punt d’intersecció de les diagonals i, en un cilindre, en el punt mitjà que uneix el centre de les bases: El centre de gravetat dels cossos regulars, com un rectangle o un cilindre, coincideix aproximadament amb el centre geomètric del cos. El concepte de centre de gravetat també és aplicable a sistemes compostos per diversos cossos: si un objecte és format per N parts, cadascuna de massa m, situades a una distància x del centre de coordenades, la coordenada horitzontal del centre de gravetat vindrà donada per aquesta expressió: Índex

2. Equilibri de forces 2. 1. Centre de gravetat Índex

3. Forces i deformacions Alguns sòlids, quan se’ls aplica una força, es deformen lleugerament. Aquest és el cas dels sòlids elàstics. Una propietat important d’aquest tipus de sòlids és que, quan la força deixa d’actuar-hi, recuperen la forma original. Pot passar que si la deformació és produïda per una força molt gran, arriba un moment que el sòlid ja no recupera la forma original i queda permanentment deformat. Aquestes deformacions s’anomenen deformacions plàstiques. Si seguim augmentant la tensió sobre el material, arribarà un moment que es començarà a trencar. El límit entre les forces que causen una deformació plàstica i les forces que provoquen l’inici del trencament del material s’anomena límit de trencament. Depenent de la força que apliquem sobre un cos, es comportarà de manera diferent. Corba de deformació d’un material típic: al principi la tensió és lineal amb la deformació (deformació elàstica), després té un altre comportament (deformació plàstica) i, finalment, disminueix (això indica que hem sobrepassat el límit de trencament). Índex

3. Forces i deformacions 3. 1. La llei de Hooke Alguns objectes elàstics tenen una propietat especial: quan els apliquem una força constant F, experimenten una deformació que és proporcional a aquesta mateixa força. Això vol dir que si, per exemple, doblem la força que estem aplicant sobre un objecte elàstic, la deformació que observem també serà el doble. Representació de la llei de Hooke per una molla: si la força que actua sobre una molla dobla el seu valor, l’allargament de la molla també es dobla. Un exemple familiar d’aquest tipus d’objectes són les molles. Si es penja una molla en posició vertical i s’hi col·loca un pes, la molla s’estirarà en proporció al pes que hi hem posat; si es dobla el pes, es duplicarà l’allargament de la molla. Índex

3. Forces i deformacions 3. 1. La llei de Hooke Aquests tipus d’objectes satisfan l’anomenada llei de Hooke, segons la qual les forces aplicades sobre un cos elàstic són directament proporcionals a la deformació (allargament o escurçament) que produeixen. L’equació que descriu la llei de Hooke és aquesta: F = k · ∆L K és una constant anomenada constant elàstica, que depèn del tipus de material elàstic sota consideració. Aquesta constant ens dóna una idea del que costa d’estirar o arronsar. Les unitats d’aquesta constant en el Sistema Internacional són N/m, com es pot veure a partir de l’equació de la llei de Hooke. ∆L és la deformació produïda per la força F: ∆ L = L · L 0 és la longitud natural de la molla, és a dir, la longitud quan no hi actua cap força. Índex

3. Forces i deformacions 3. 1. La llei de Hooke Índex

3. Forces i deformacions 3. 2. El dinamòmetre és un aparell, inventat per Isaac Newton, que es fa servir al laboratori per mesurar forces. El funcionament del dinamòmetre es basa en la llei de Hooke, segons la qual les deformacions són proporcionals a les forces. El dinamòmetre consisteix en una molla continguda dins d’un cilindre –generalment de plàstic, cartró o metall– amb dos ganxos, un en cada extrem. Els dinamòmetres tenen marcada una escala en unitats de força, de manera que en exercir una força sobre un dels ganxos el cursor del cilindre es desplaça sobre l’escala que té marcada i indica el valor de la força exercida. Dinamòmetre mecànic. Índex Dinamòmetre electrònic.

3. Forces i deformacions 3. 2. El dinamòmetre Calibratge d’un dinamòmetre Quan desconeixem la constant elàstica k del dinamòmetre, abans de res hem de calibrar l’aparell. Ho podem fer exposant el dinamòmetre a diferents forces de valor conegut i mesurant el desplaçament que produeixen. Posteriorment, calculem per a cada cas el valor de la constant elàstica, mitjançant la llei de Hooke: Si prenem la mitjana dels resultats obtinguts, podem determinar el valor de k. Índex

3. Forces i deformacions 3. 2. El dinamòmetre Índex

4. La pressió és el quocient entre la intensitat de la força F que s’aplica perpendicularment sobre una superfície i l’àrea d’aquesta superfície. Les unitats de la pressió, a partir de la seva definició, són N/m 2, que també s’anomenen pascal (Pa) en el Sistema Internacional d’unitats. Com que la pressió és el quocient entre la força aplicada i la superfície on s’aplica la força, si reduïm pel mateix factor la força aplicada i la superfície obtenim la mateixa pressió. Índex

4. La pressió En determinades situacions ens interessa tenir pressions petites i en d’altres, pressions grans. Per exemple, és molt més fàcil clavar un clau amb punta que no pas un clau despuntat, ja que en el primer cas la superfície de contacte és molt inferior i, per tant, la pressió que s’exerceix és molt més gran. En canvi, quan anem a esquiar ens posem uns esquís que tenen una superfície molt més gran que els nostres peus, per tal d’exercir una pressió molt més petita i no enfonsar-nos en la neu. Índex

4. La pressió 4. 1. La pressió en fluids El concepte de pressió també es pot aplicar a fluids, és a dir, a líquids i a gasos, però el tractament és una mica diferent. Si apliquem una pressió a un sòlid es deforma lleugerament, quan apliquem pressió a un fluid la seva forma canvia completament. En els cas dels líquids, la pressió que exerceixen les molècules a causa del seu pes s’anomena pressió hidrostàtica. La pressió hidrostàtica que exerceix una columna d’altura h i secció S deguda a la força de la gravetat es calcula de la manera següent: Primer de tot, calculem la massa de la columna d’aigua que tenim, fent servir la densitat ρ del líquid: Per tant, la força total que exercirà la gravetat sobre aquesta massa serà aquesta: La pressió hidrostàtica que exerceix la columna vindrà donada per aquesta equació: Índex

4. La pressió 4. 2. La pressió atmosfèrica En el cas d’un gas, la pressió es pot calcular exactament de la mateixa manera que en el cas dels líquids. La diferència principal és que en els gasos les densitats típiques són molt inferiors a les dels líquids. La pressió atmosfèrica és la pressió que exerceix l’aire de l’atmosfera sobre la superfície de la Terra. Càlcul de la pressió atmosfèrica El càlcul que farem sobre la pressió atmosfèrica serà necessàriament una aproximació, ja que el perfil de densitat i composició de l’atmosfera varia amb l’altura. Fem servir la fórmula de la pressió hidrostàtica aplicada a la nostra atmosfera: Patm = ρaire · g · hatmosfera Índex

4. La pressió 4. 2. La pressió atmosfèrica Les dades experimentals que necessitem per calcular aproximadament la pressió atmosfèrica són l’alçada de l’atmosfera (prenem h = 15 km) i la densitat mitjana (prenem ρ = 0, 8 kg/m 3). Per tant, prenent l’acceleració de la gravetat com a 10 m/s 2 (per arrodonir els valors numèrics), obtenim que: Patm = 0, 8 kg/m 3 · 10 m/s 2 · 15. 000 m = 120. 000 Pa Ara ja podem comparar aquesta dada amb el valor exacte: Patmosfèrica = 101. 000 Pa Aquesta estimació és raonable, però per calcular el valor exacte s’ha de fer servir un model més complet de l’atmosfera. Per mesurar la pressió atmosfèrica, en comptes del pascal s’utilitza una altra unitat: l’atmosfera. Una atmosfera és la pressió atmosfèrica sobre la superfície terrestre i equival, com acabem de veure, a 1 atm = 1, 01 · 105 Pa Aquesta unitat és més útil per mesurar pressions com les que realitzen l’atmosfera prop de la superfície terrestre, els avions o fins i tot els vehicles espacials. Índex

4. La pressió 4. 2. La pressió atmosfèrica El valor de la pressió atmosfèrica varia constantment al llarg del temps i en diferents indrets, a causa d’una sèrie de factors que defineixen el clima global, com per exemple: • La relació entre les temperatures de masses d’aire properes i la seva interacció amb el mar i la superfície terrestre. • Les variacions cícliques diàries degudes a marees atmosfèriques globals. • El moviment de grans masses d’aire. • Les forces de tipus Coriolis. Les regions amb una pressió atmosfèrica baixa generen tempestes, fortes precipitacions i, fins i tot, ocasionalment, ciclons o tornados, els quals tenen una regió de molt baixa pressió al centre. En canvi, les regions amb una pressió atmosfèrica elevada estan associades al temps estable. Índex

4. La pressió 4. 2. La pressió atmosfèrica En els mapes del temps que observem diàriament a les notícies es mostren les isòbares, línies que uneixen els punts on hi ha la mateixa pressió atmosfèrica. Mapamundi de la pressió atmosfèrica. Les línies contínues són les isòbares. Índex

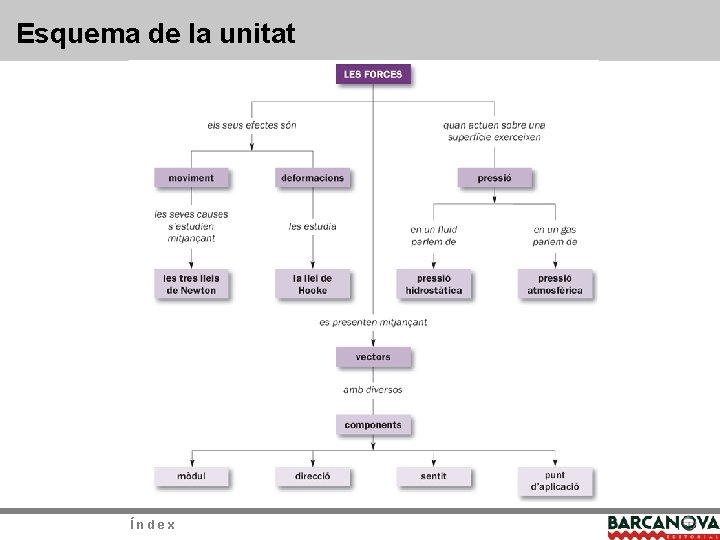
Esquema de la unitat Índex