UNIT2 PULIC KEY CRYPTOGRAPHY AND MESSAGE AUTHENTICATION Approaches

UNIT-2 PULIC –KEY CRYPTOGRAPHY AND MESSAGE AUTHENTICATION

Approaches to message Authentication Secure Hash Functions and HMAC Public – Key Cryptography Principles Public – Key Cryptography Algorithms NETWORK SECURITY By: Homera Durani 2

Approaches To Message Authentication �Confidentiality – protection from passive attacks �Authentication – you are who you say you are �Integrity – received as sent, no modifications, insertions, shuffling or replays NETWORK SECURITY By: Homera Durani 3

Security Attacks � Message authentication helps prevents these Active threats Masquerade Replay Modification of message contents Denial of service Protection against attacks is known as message authentication. NETWORK SECURITY By: Homera Durani 4

What is Message Authentication �It’s the “source, ” of course! �Procedure that allows communicating parties to verify that received messages are authentic �Characteristics: � source is authentic – masquerading � contents unaltered – message modification � timely sequencing – replay NETWORK SECURITY By: Homera Durani 5

Use of Conventional Encryption? �Only sender and receiver share a key �Include a time stamp �Include error detection code and sequence number NETWORK SECURITY By: Homera Durani 6

Message Authentication without Confidentiality �Application that broadcasts a message – only one destination needs to monitor for authentication �Too heavy a load to decrypt – random authentication checking, messages are chosen at random for checking. �Computer executables and files – checked when assurance required. NETWORK SECURITY By: Homera Durani 7

Life Without Authentication NETWORK SECURITY By: Homera Durani 8

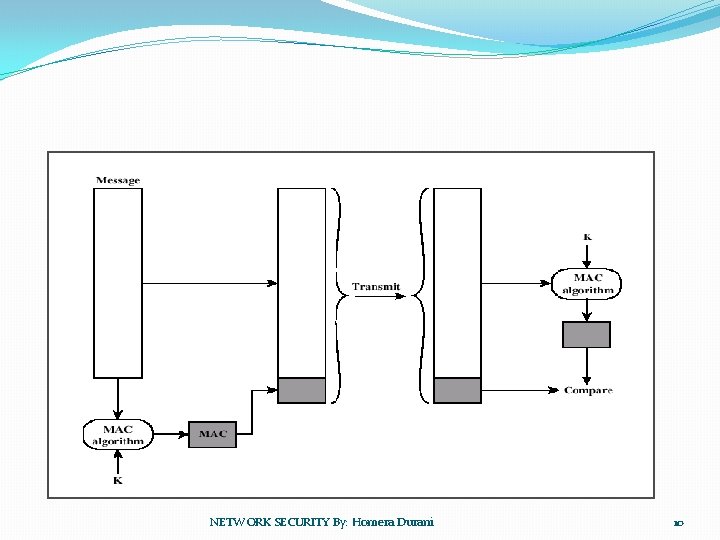
Message Authentication Code �Message Authentication Code (MAC) – use a secret key to generate a small block of data that is appended to the message �Assume: A and B share a common secret key KAB �MACM = F(KAB, M) NETWORK SECURITY By: Homera Durani 9

NETWORK SECURITY By: Homera Durani 10

�Receiver assured that message is not altered – no modification �Receiver assured that the message is from the alleged sender – no masquerading �Include a sequence number, assured proper sequence – no replay NETWORK SECURITY By: Homera Durani 11

�DES is used �Need not be reversible �Checksum �Stands up to attack �But there is an alternative. . . NETWORK SECURITY By: Homera Durani 12

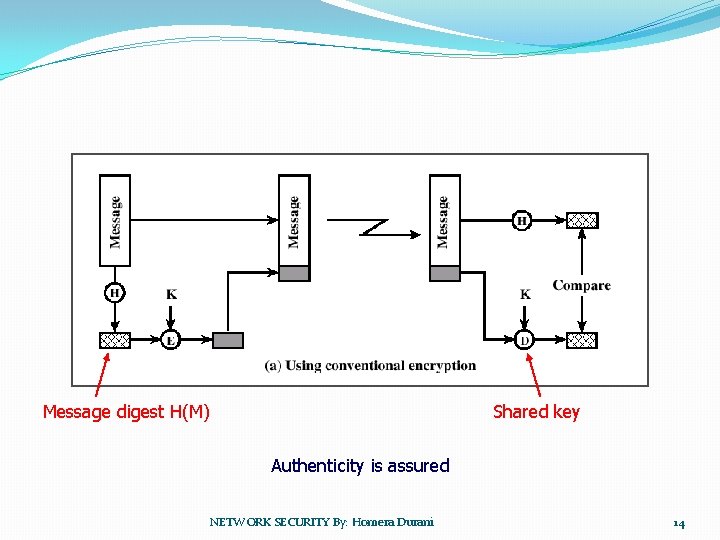
One Way Hash Function �Hash function accepts a variable size message M as input and produces a fixed-size message digest H(M) as output �No secret key as input �Message digest is sent with the message for authentication �Produces a fingerprint of the message NETWORK SECURITY By: Homera Durani 13

Message digest H(M) Shared key Authenticity is assured NETWORK SECURITY By: Homera Durani 14

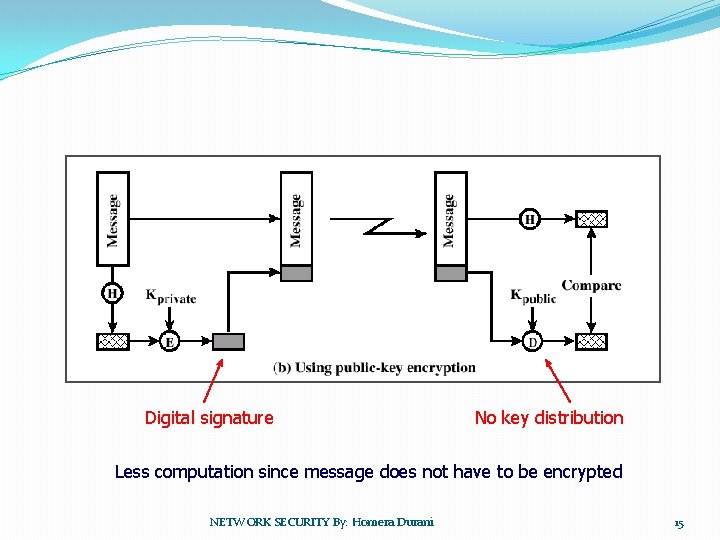
Digital signature No key distribution Less computation since message does not have to be encrypted NETWORK SECURITY By: Homera Durani 15

�Encryption software is slow �Encryption hardware costs aren’t cheap �Hardware optimized toward large data sizes �Algorithms covered by patents �Algorithms subject to export control �Thus ONE AVOID ENCRYPTION NETWORK SECURITY By: Homera Durani 16

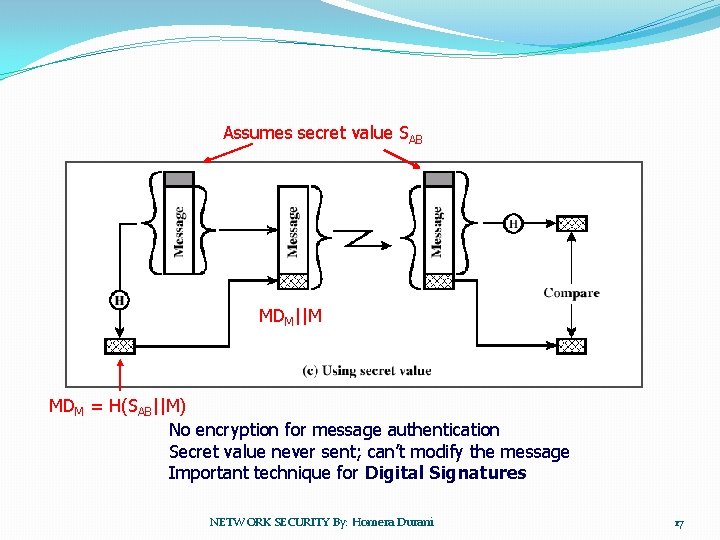
Assumes secret value SAB MDM||M MDM = H(SAB||M) No encryption for message authentication Secret value never sent; can’t modify the message Important technique for Digital Signatures NETWORK SECURITY By: Homera Durani 17

SECURE HASH FUNCTIONS AND HMAC NETWORK SECURITY By: Homera Durani 18

HASH Function Requirements �The purpose of a hash function is to produce a “fingerprint” of a file, message, or other block of data, a hash function H must have the following properties: 1. H can be applied to a block of data at any size 2. H produces a fixed length output 3. H(x) is easy to compute for any given x. 4. For any given block x, it is computationally infeasible to find x such that H(x) = h 5. For any given block x, it is computationally infeasible to find with H(y) = H(x). 6. It is computationally infeasible to find any pair (x, y) such that H(x) = H(y) NETWORK SECURITY By: Homera Durani 19

Simple Hash Functions NETWORK SECURITY By: Homera Durani 20

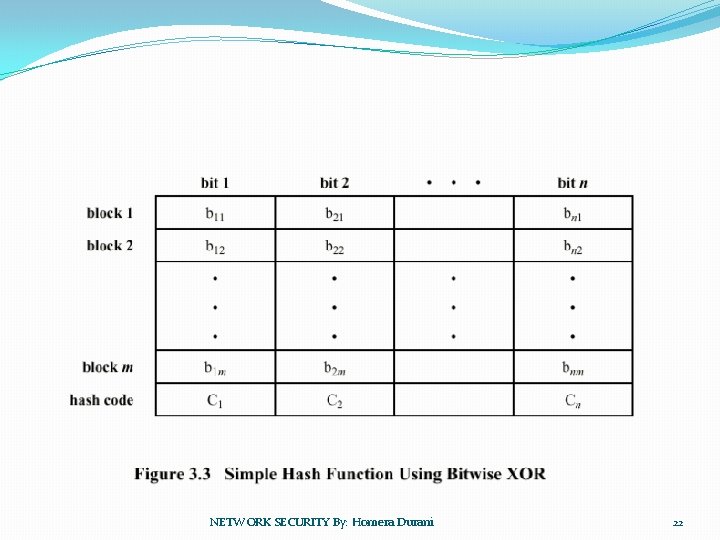
�One of the simplest hash functions is the bit – by – bit exclusive OR(XOR) of every block which can be expressed as follows: �Ci= bi 1 ⊕ bi 2 ⊕ … ⊕ bim. �Where � Ci= ith bit of the hash code , 1<= i<= n � M = number of n- bit blocks in the input. � Bij = ith bit in jth block � ⊕ = XOR operation NETWORK SECURITY By: Homera Durani 21

NETWORK SECURITY By: Homera Durani 22

�A simple way to improve is to perform a one- bit circular shift, or rotation on the hash value after each block is processed. The procedure can be summarized as follows : � 1. Initially set the n- bit hash value to zero. � 2. Process each successive n – bit block of the data as follows: a. Rotate the current hash value to the left by one bit. b. XOR the block into the hash value. NETWORK SECURITY By: Homera Durani 23

SHA -1 Secure Hash Function NETWORK SECURITY By: Homera Durani 24

�SHA (Secure Hash Algorithm ) was developed by the National Institute of Standards and Technology (NIST) and published as a federal information processing standard (FIPS 180) in 1993. �SHA -1 produces a hash value of 160 bits. In 2002 , NIST produced a new version of the standard, FIPS 180 -2 , defined three new version of SHA with hash value lengths of 256, 384 , and 512 bits. �Which were known as SHA-256, SHA-384, SHA -512. NETWORK SECURITY By: Homera Durani 25

�Comparison of SHA Parameters. NETWORK SECURITY By: Homera Durani 26

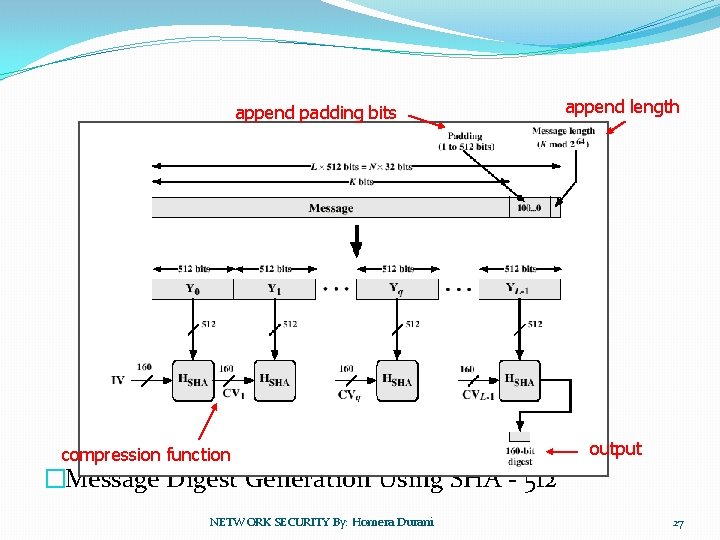
append padding bits compression function append length output �Message Digest Generation Using SHA - 512 NETWORK SECURITY By: Homera Durani 27

�Input is processed in 512 -bit blocks �Produces as output a 160 -bit message digest �Every bit of the hash code is a function of every bit of the input NETWORK SECURITY By: Homera Durani 28

NETWORK SECURITY By: Homera Durani 29

Other Secure Hash Function �Most follow basic structure of SHA-1 �This is also called an iterated hash function – Ralph Merkle 1979 �If the compression function is collision resistant, then so is the resultant iterated hash function NETWORK SECURITY By: Homera Durani 30

Other Secure Hash Function �MD 5 �Whirlpool NETWORK SECURITY By: Homera Durani 31

MD 5 �Message Digest Algorithm (MD 5) was developed by Ron Rivest. �Ron Rivest - 1992 �RFC 1321 �Input: arbitrary Output: 128 -bit digest �Most widely used secure hash algorithm – until recently �Security of 128 -bit hash code has become questionable (1996, 2004) NETWORK SECURITY By: Homera Durani 32

Whirlpool �Developed by Vincent Rijmen who is co –inventor of Rijndael. �Whirlpool is one of the two hash Function endorsed by NESSIE (New European Schemes for Signatures, Integrity, and Encryption ). �Whirlpool is based on the use of a block cipher for the compression function. �It is based on AES. �Algorithm takes input less than 2256 bit Output a 512 – bit. NETWORK SECURITY By: Homera Durani 33

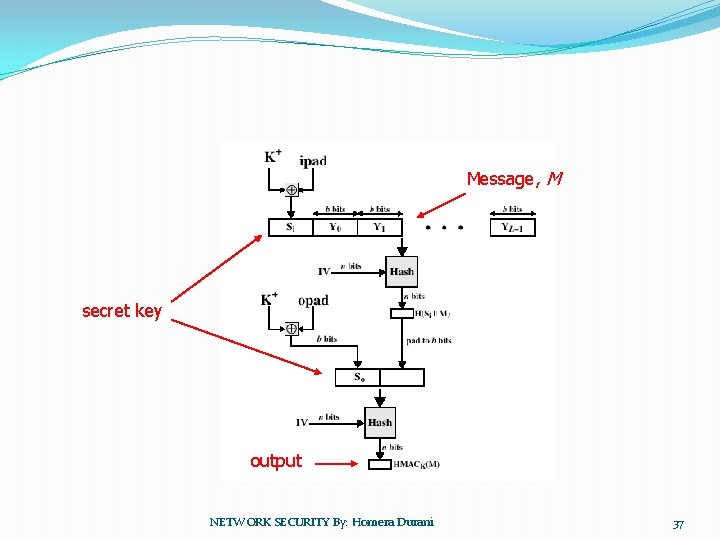
HMAC �Effort to develop a MAC derived from a cryptographic hash code �Executes faster in software �No export restrictions �Relies on a secret key �RFC 2104 list design objectives �Used in Ipsec �Simultaneously verify integrity and authenticity NETWORK SECURITY By: Homera Durani 34

�Motivations: �Cryptographic hash functions executes faster in software than encryptoin algorithms such as DES �Library code for cryptographic hash functions is widely available �No export restrictions from the US �HMAC has been issued as RFC 2104 and has been chosen as the mandatory – to – implement MAC for IP security , and used in other Internet Protocols such as TLS(Transport Layer Security ) to replace SSL(Secure Sockets Layer) and SET(Secure Electronic Transaction). NETWORK SECURITY By: Homera Durani 35

Objectives � To use, without modifications , available in Hash Functions �Easy Replace ability. �Preserve original performance. �Use and handle keys in a simple way. NETWORK SECURITY By: Homera Durani 36

Message, M secret key output NETWORK SECURITY By: Homera Durani 37

Public – Key Cryptography principles NETWORK SECURITY By: Homera Durani 38

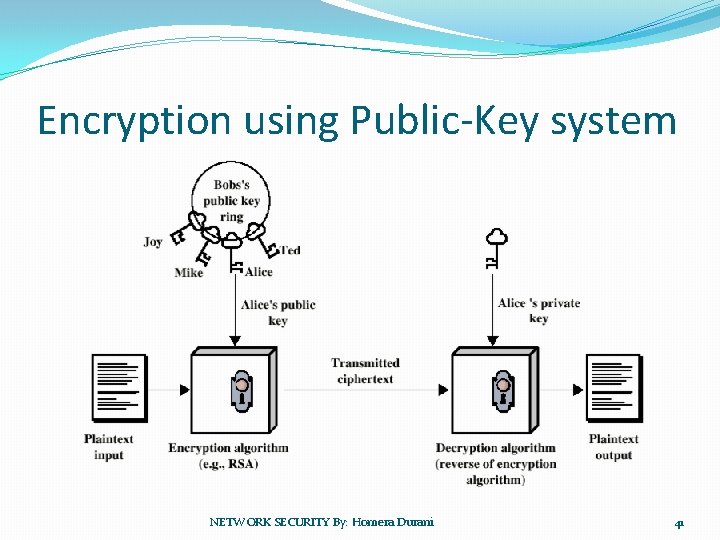
Public – key Encryption Structure �The use of two keys has consequences in: key distribution, confidentiality and authentication. �The scheme has six ingredients �Plaintext �Encryption algorithm �Public and private key �Ciphertext �Decryption algorithm NETWORK SECURITY By: Homera Durani 39

�Plaintext : Readable message. �Encryption Algorithm : performs various transformation on the plaintext. �Public and Private key : one is used for encryption and other is used for decryption. �Cipher text : scrambled message (output). �Decryption algorithm : accepts cipher text and match key and produce original plaintext. NETWORK SECURITY By: Homera Durani 40

Encryption using Public-Key system NETWORK SECURITY By: Homera Durani 41

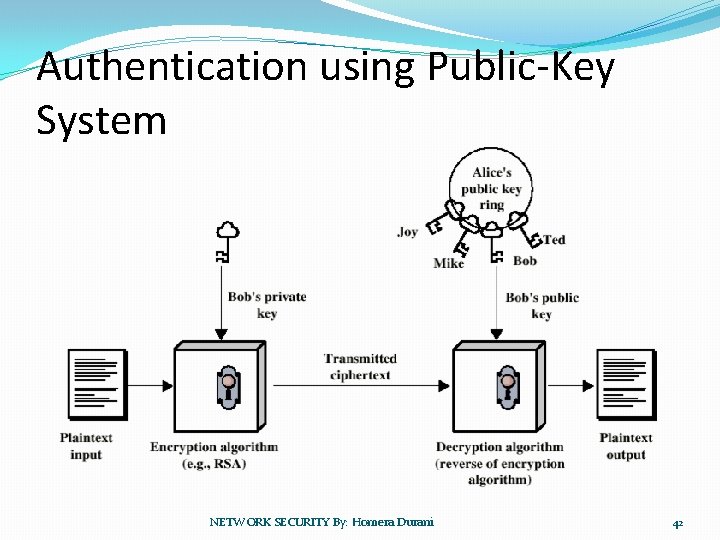
Authentication using Public-Key System NETWORK SECURITY By: Homera Durani 42

Applications for Public-Key Cryptosystems �Three categories: �Encryption/decryption: The sender encrypts a message with the recipient’s public key. �Digital signature: The sender ”signs” a message with its private key. �Key exchange: Two sides cooperate two exhange a session key. NETWORK SECURITY By: Homera Durani 43

Requirements For Public Key �Easy for party B to generate pairs: public key KUb ; private key KRb �Easy for sender A to generate cipertext using public key: C = E KUb(M) �Easy for receiver B to decrypt using the private key to recover original message M = DKRb(C) = DKRb[E KUb(M)] HINT: PUBLIC PRIVATE NETWORK SECURITY By: Homera Durani 44

� � � It is computationally infeasible for an opponent, knowing the public key KUb to determine the private key KRb It is computationally infeasible for an opponent, knowing the public key KUb and a ciphertext, C, to recover the original message, M Either of the two related keys can be used for encryption, with the other used for decryption M = DKRb[EKUb(M)]= DKUb[EKRb(M)] NETWORK SECURITY By: Homera Durani 45

Public – key Cryptography Algorithms NETWORK SECURITY By: Homera Durani 46

Public-Key Cryptographic Algorithms �RSA and Diffie-Hellman �RSA - Ron Rivest in 1977, Adi Shamir and Len Adleman at MIT, and published in 1978. �RSA is a block cipher �The most widely implemented �Diffie-Hellman �Echange a secret key securely �Compute discrete logarithms NETWORK SECURITY By: Homera Durani 47

RSA Algorithm � � � Most widely accepted and implemented approach to public key encryption Block cipher where M and C are integers between 0 and n 1 for some n Following form: C = Me mod n M = Cd mod n = (Me)d mod n = Med mod n NETWORK SECURITY By: Homera Durani 48

�Sender and receiver know the values of n and e, but only the receiver knows the value of d �Public key: KU = {e, n} �Private key: KR = {d, n} NETWORK SECURITY By: Homera Durani 49

RSA Requirements �It is possible to find values of e, d, n such that Med = M mod n for all M<n �It is relatively easy to calculate Me and C for all values of M<n �It is infeasible to determine d given e and n Here is the magic! NETWORK SECURITY By: Homera Durani 50

NETWORK SECURITY By: Homera Durani 51

NETWORK SECURITY By: Homera Durani 52

RSA Example � � � Select two prime numbers, p=7 and q=11 Calculate n = pq = 7 x 11 = 187 Calculate (n) = (p-1)(q-1) = 16 * 10 = 160 Select e such that e is relatively prime to (n) = 160 and less than (n) ; in this case, e= 7 Determine d such that de = 1 mod 160 and d<160. The correct value is d = 23, because 23 x 7 = 161 = 10 x 160+ 1 NETWORK SECURITY By: Homera Durani 53

�Plain text 88 �Cipher text 11 and output plaintext 88 Encryption Decryption 88 7 mod 187 = 11 �Pu = 7, 187 11 23 mod 187 = 88 pr = 23, 187 NETWORK SECURITY By: Homera Durani 54

RSA Encryption �Plaintext: �Ciphertext: M<n C = Me (mod n) NETWORK SECURITY By: Homera Durani 55

RSA Decryption �Cipher text: �Plaintext: C M = Cd (mod n) NETWORK SECURITY By: Homera Durani 56

RSA Strength �Brute force attack: try all possible keys – the larger e and d the more secure �The larger the key, the slower the system �For large n with large prime factors, factoring is a hard problem �Cracked in 1994 a 428 bit key; $100 �Currently 1024 key size is considered strong enough NETWORK SECURITY By: Homera Durani 57

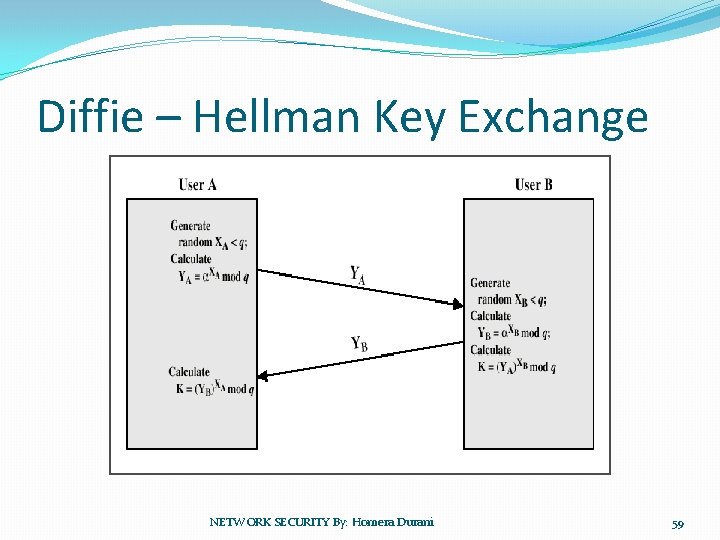
Diffie- Hellman key Exchange NETWORK SECURITY By: Homera Durani 58

Diffie – Hellman Key Exchange NETWORK SECURITY By: Homera Durani 59

Other Public-Key Cryptographic Algorithms �Digital Signature Standard (DSS) �Makes use of the SHA-1 �Not for encryption or key echange �Elliptic-Curve Cryptography (ECC) �Good for smaller bit size �Low confidence level, compared with RSA �Very complex NETWORK SECURITY By: Homera Durani 60