UNIT1 Vector Unit1 Review of Vector Analysis Cartesian

















































- Slides: 90

UNIT-1 Vector

Unit-1: Review of Vector Analysis �Cartesian, �Cylindrical and �Spherical Co-ordinate Systems, �Vector products, �Projection of Vectors, �Gradient, �Divergence �Curl, �Line, surface, volume integrals, �Divergence Theorem �Stokes theorem

Unit-2 Electrostatics: �Coulomb’s Law, �Electric field intensity, �Evaluation of Electric field intensity due to line charge, Surface charge and Volume charge distribution, �Electric flux density, �Gauss Law, �Electrostatic potential, �Potential gradient, �Electric dipole and Polarization

Unit-3 Magnetostatics : �Biot–Savart Law, �Ampere’s Circuital Law, � Magnetic field intensity, �Magnetic field intensity evaluation due to infinite, finite and circular current carrying conductors, �Magnetic flux �Flux density, �Magnetic dipole and Magnetization

Unit-4 Boundary Conditions & Maxwell’s Equations : �Boundary condition at Dielectric – Conductor interface, Dielectric – Dielectric interface, �Boundary conditions for magnetic materials interface, �Current continuity equation, � Maxwell’s equations.

Unit-5 Electromagnetic wave propagation : �Electromagnetic wave equation for free space, lossy dielectric material and perfect conductor, �Propagation constant, � Attenuation constant & Phase shift constant, �Skin depth, �Poynting Theorem, �Reflection of a plain wave in a normal incidence at Dielectric – Dielectric interface, Dielectric – Conductor interfaces

Unit-6 Radiation: : �Scalar and Vector magnetic potential, Retarded potential, Electric & Magnetic fields, �Power radiated and Radiation resistance due to oscillating dipole, Quarter wave monopole & Half wave dipole.

Unit-5 Electromagnetic wave propagation: Electromagnetic wave equation for free space, lossy dielectric material and perfect conductor, Propagation constant, Attenuation constant & Phase shift constant, Skin depth, Poynting Theorem, Reflection of a plain wave in a normal incidence at Dielectric – Dielectric interface, Dielectric – Conductor interfaces. 10 Unit-6 Radiation: Scalar and Vector magnetic potential, Retarded potential, Electric & Magnetic fields, Power radiated and Radiation resistance due to oscillating dipole, Quarter wave monopole & Half wave dipole.

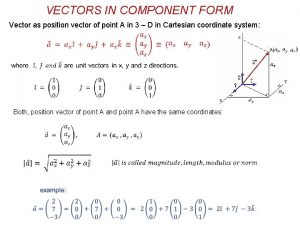
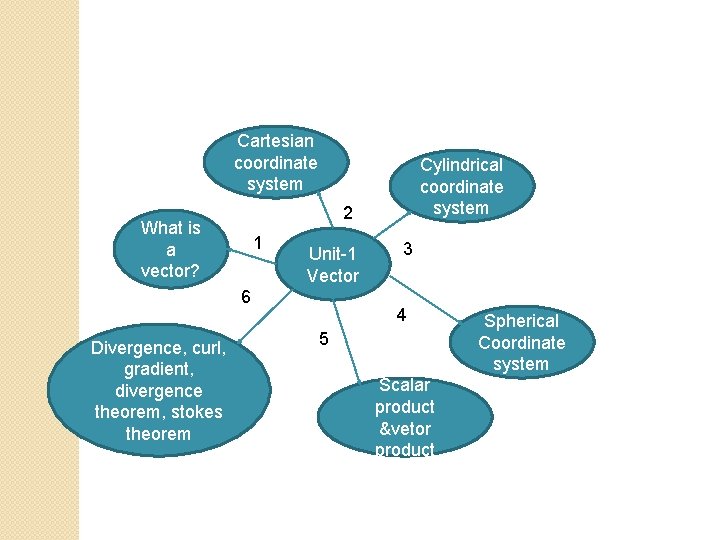
Cartesian coordinate system 2 What is a vector? 1 Unit-1 Vector 6 Divergence, curl, gradient, divergence theorem, stokes theorem Cylindrical coordinate system 3 4 5 Scalar product &vetor product Spherical Coordinate system

Vector analysis is a mathematical tool with which electromagnetic concepts are more conveniently expressed and best comprehended. Since use of vector analysis in the study of electromagnetic field theory results in real economy of time and thought.

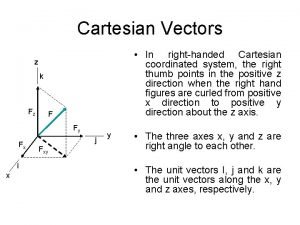
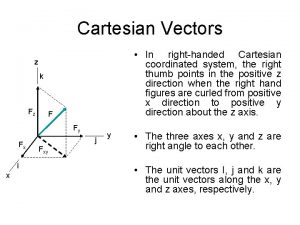
Cartesian Coordinate system Rectangle(cartisian )

Cartesian co-ordinates system i)Point ii) Differential length ii) Differential surfaces iii)Differential volume

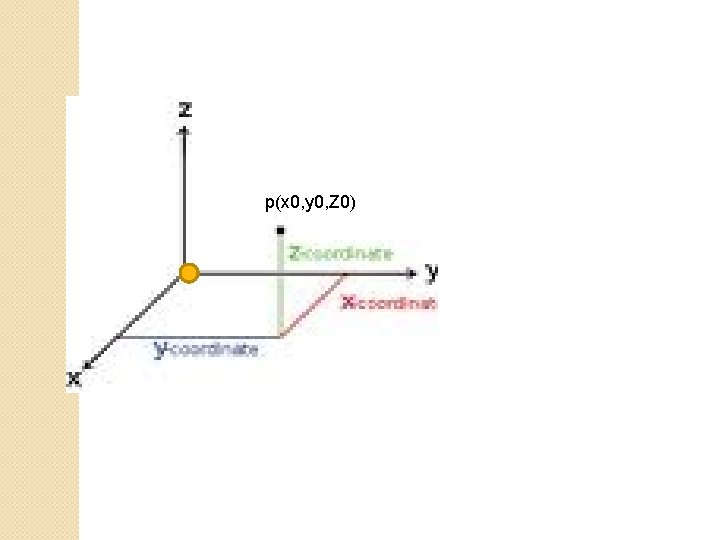
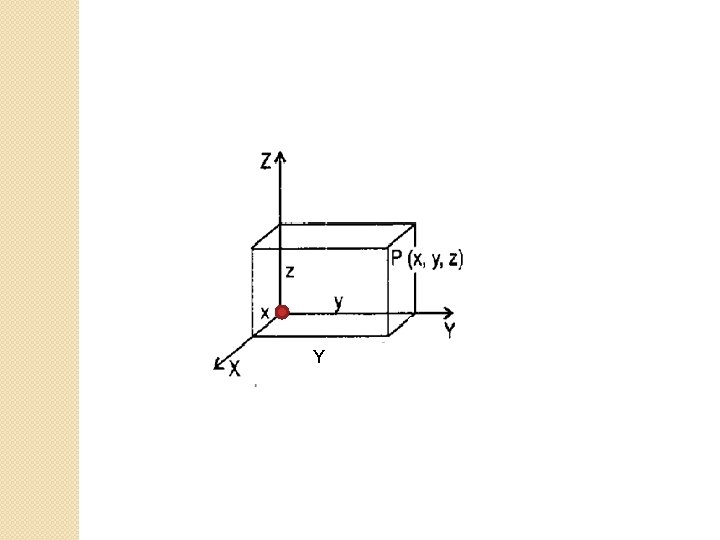
Point representation

p(x 0, y 0, Z 0)

Differential Length dz dx dy

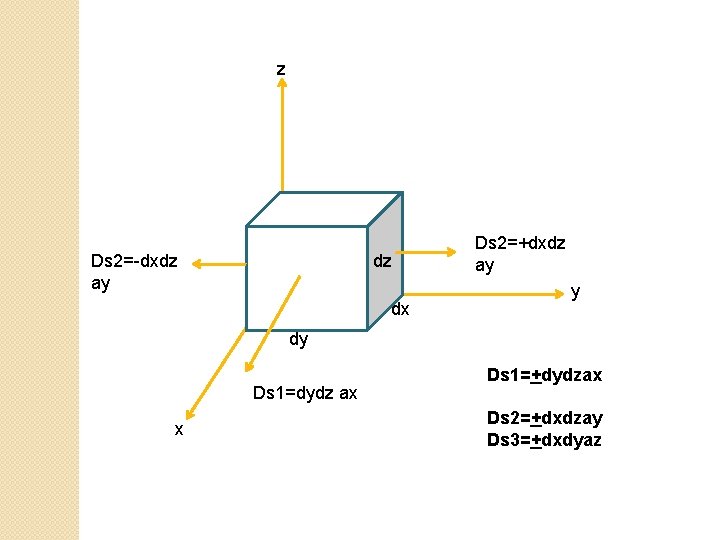
Differential Surface



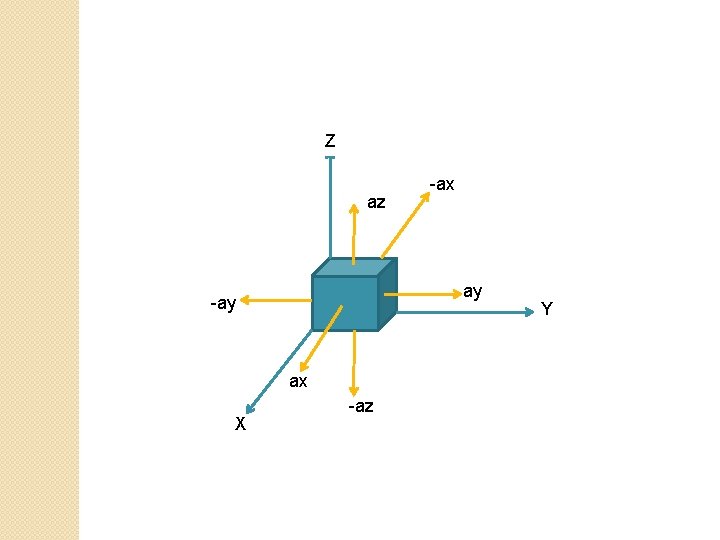
Y

Z az ay -ay ax X -ax -az Y

z Ds 2=-dxdz ay dz dx Ds 2=+dxdz ay y dy Ds 1=dydz ax x Ds 1=+dydzax Ds 2=+dxdzay Ds 3=+dxdyaz

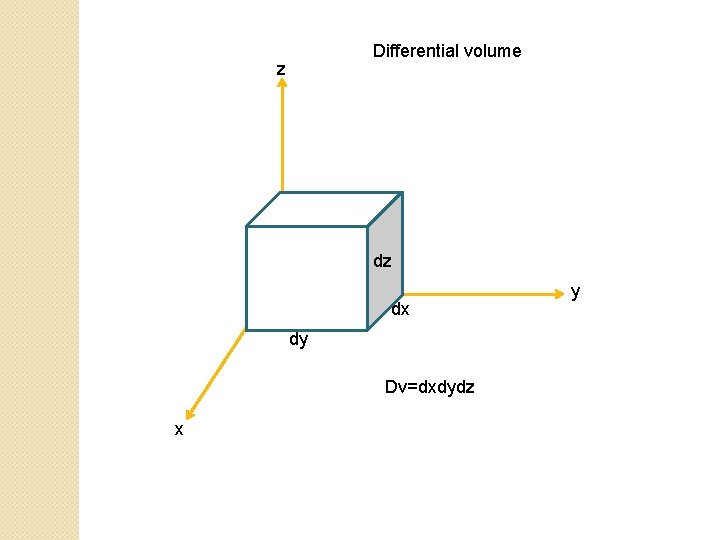
Differential Volume

Differential volume z dz dx dy Dv=dxdydz x y

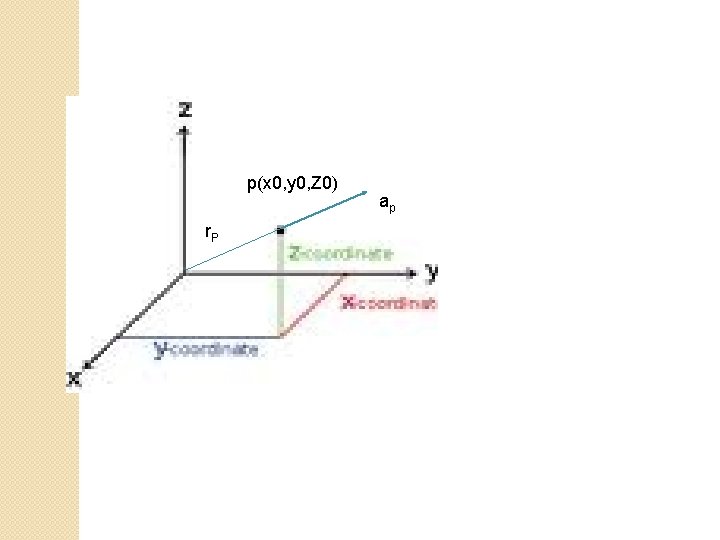
Position Vector

p(x 0, y 0, Z 0) r. P ap

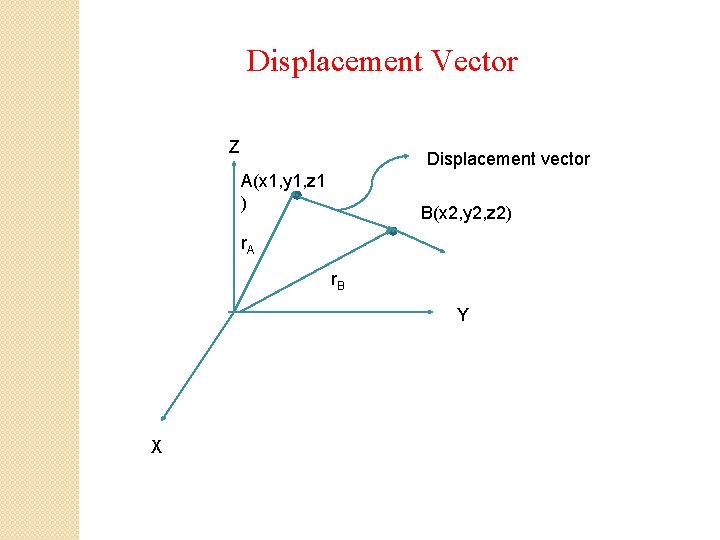
Displacement Vector Z Displacement vector A(x 1, y 1, z 1 ) B(x 2, y 2, z 2) r. A r. B Y X

Rectangular coordinate system Cylindrical coordinate system

Cylindrical Coordinate system Cylinder

CYLINDRICAL COORDINATE SYSTEM �Point �Differential length �Differential surfaces �Differential volume

Point representation

�Why did we take as a differential length in rectangular coordinate system?

p(x 0, y 0, Z 0)

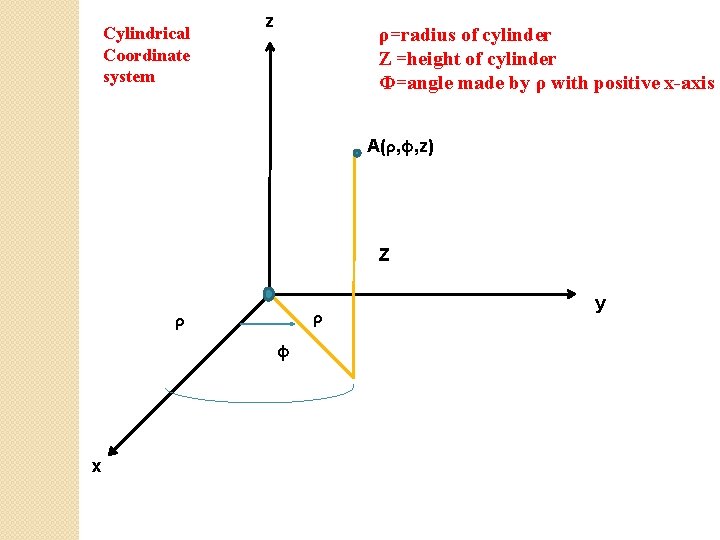
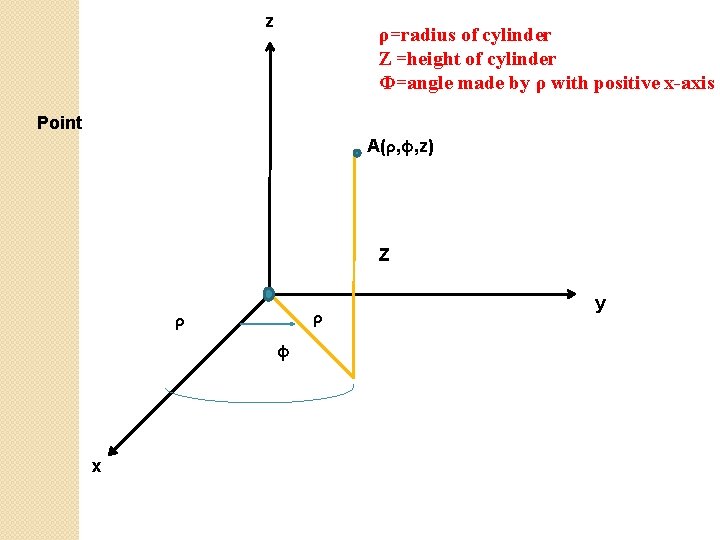
Cylindrical Coordinate system z ρ=radius of cylinder Z =height of cylinder Φ=angle made by ρ with positive x-axis A(ρ, φ, z) Z ρ ρ φ x y

z ρ=radius of cylinder Z =height of cylinder Φ=angle made by ρ with positive x-axis Point A(ρ, φ, z) Z ρ ρ φ x y

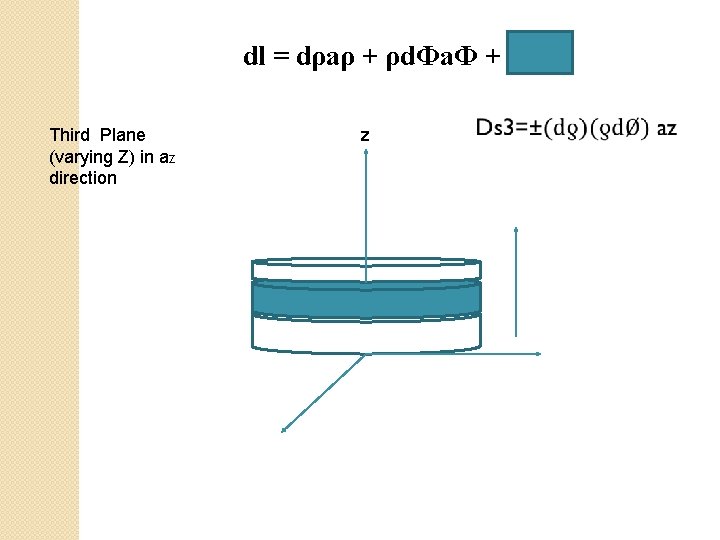
Differential Length in cylindrical coordinate system �dl = dρaρ + ρd. Фa. Ф + dz az

�Why did we take rectangular surfaces in rectangular coordinate system?

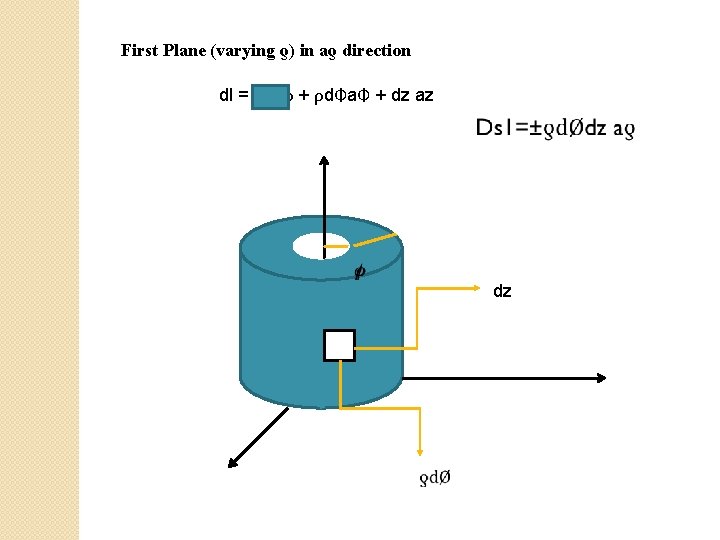
First Plane (varying ƍ) in aƍ direction dl = dρaρ + ρd. Фa. Ф + dz az dz


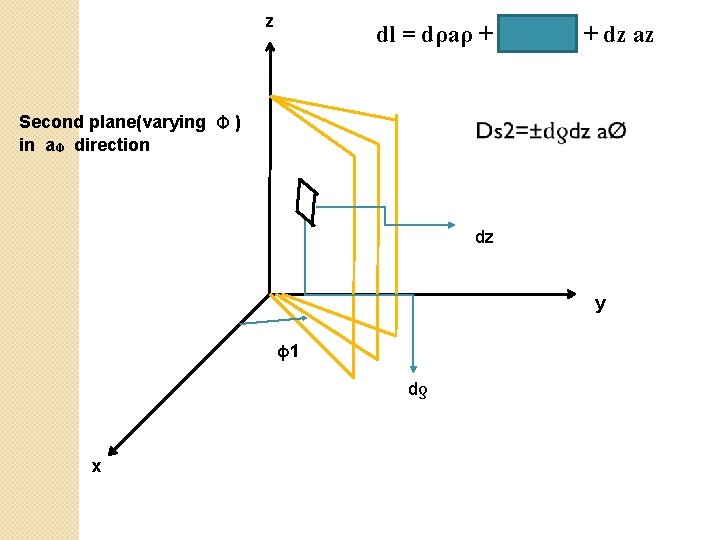
z dl = dρaρ + ρd. Фa. Ф + dz az Second plane(varying Ф ) in a. Ф direction dz y φ1 dƍ x


dl = dρaρ + ρd. Фa. Ф + dz az Third Plane (varying Z) in az direction z

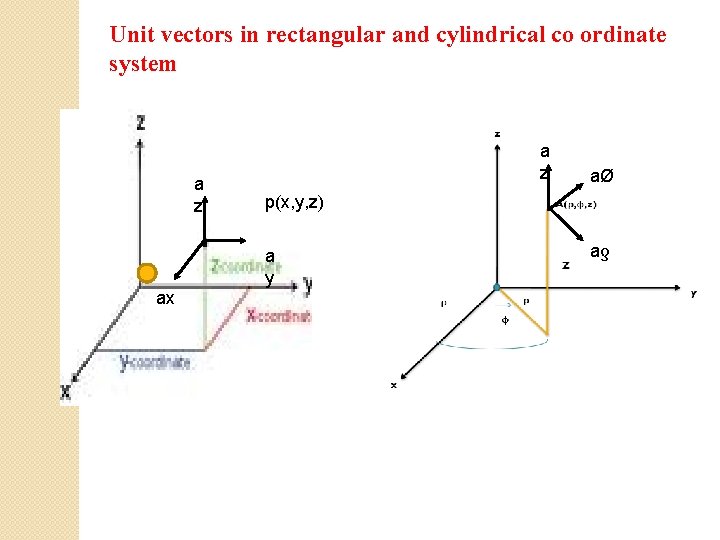
Unit vectors in rectangular and cylindrical co ordinate system a z p(x, y, z) a y ax aØ aƍ

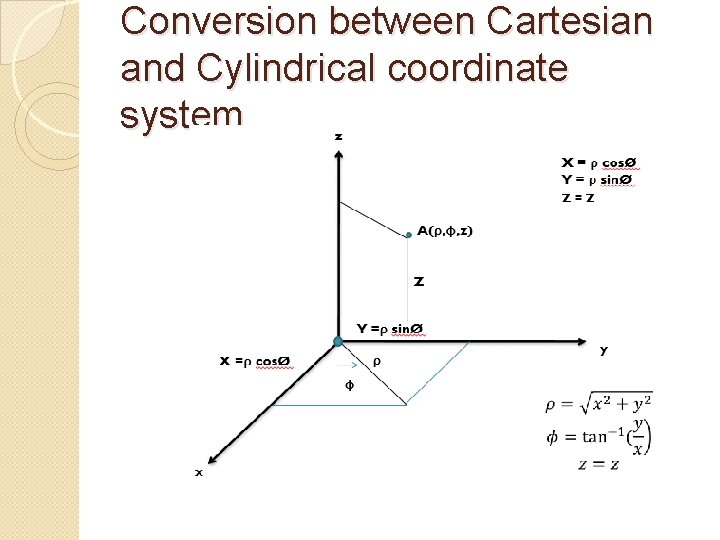
Conversion between Cartesian and Cylindrical coordinate system

Differential Length in cylindrical coordinate system �dl = dρaρ + ρd. Фa. Ф + dz az

Differential surfaces in cylindrical coordinate system �dl = dρaρ + ρd. Фa. Ф + dz az

Differential volume dv = dρρd. Фdz dv = ρdρd. Фdz

Spherical Coordinate system Sphere

Spherical Co-ordinates system i)Differential length ii)Differential surfaces iii)Differential volume

Point representation in spherical coordinate system

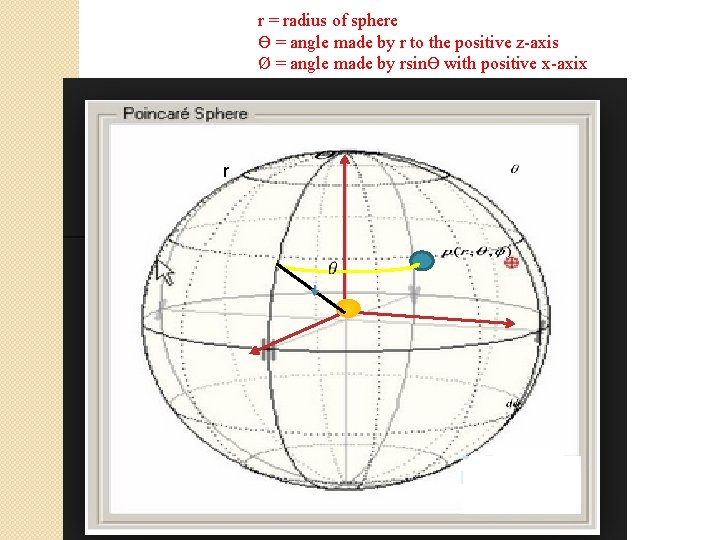
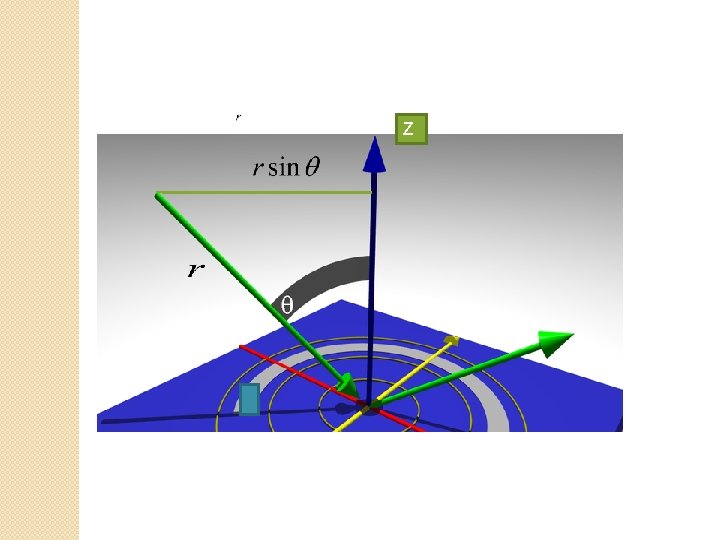
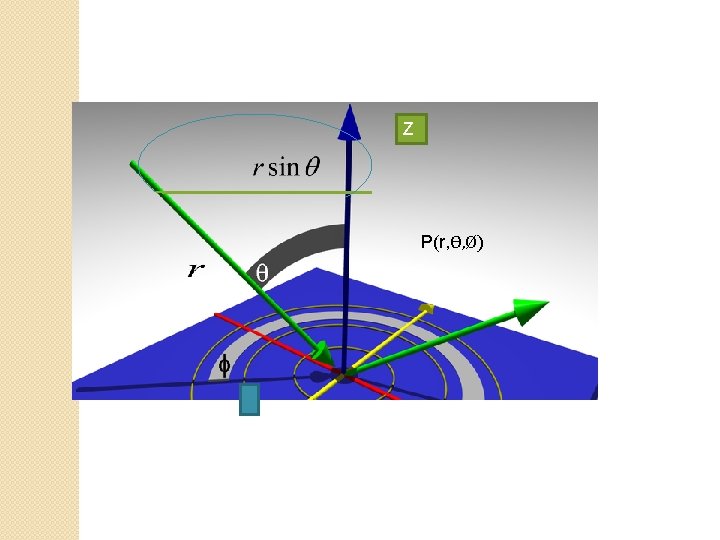
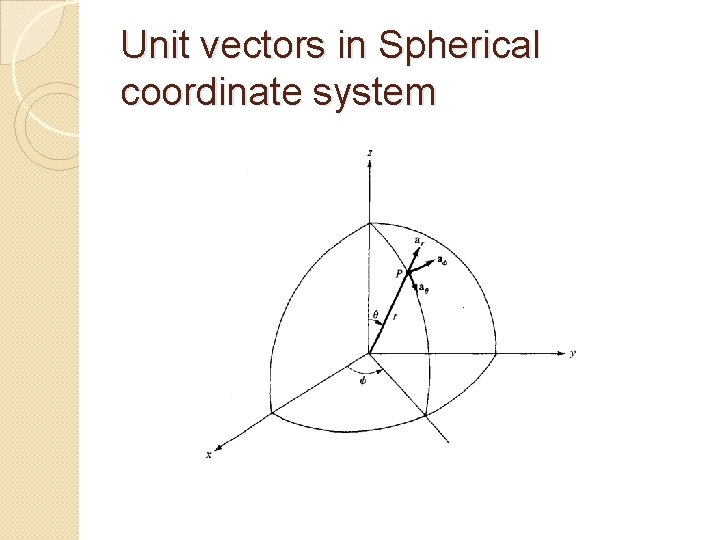
r = radius of sphere Ɵ = angle made by r to the positive z-axis Ø = angle made by rsinƟ with positive x-axix r

Z


Differential length








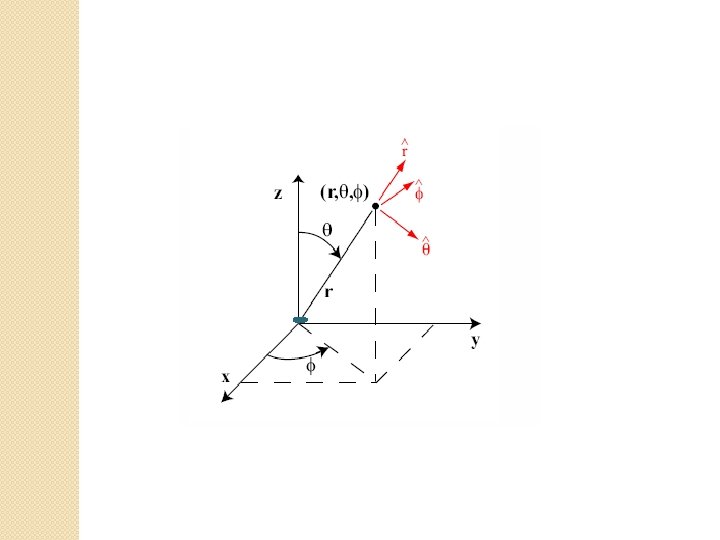
Unit vectors in Spherical coordinate system


Z





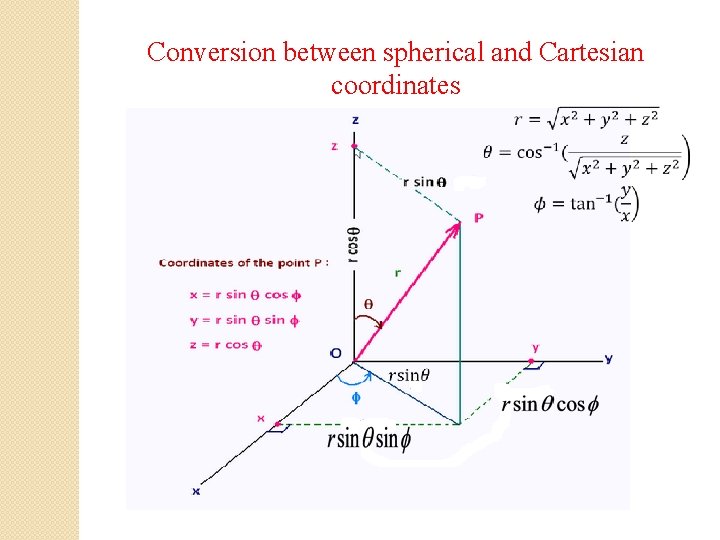
Conversion between spherical and Cartesian coordinates

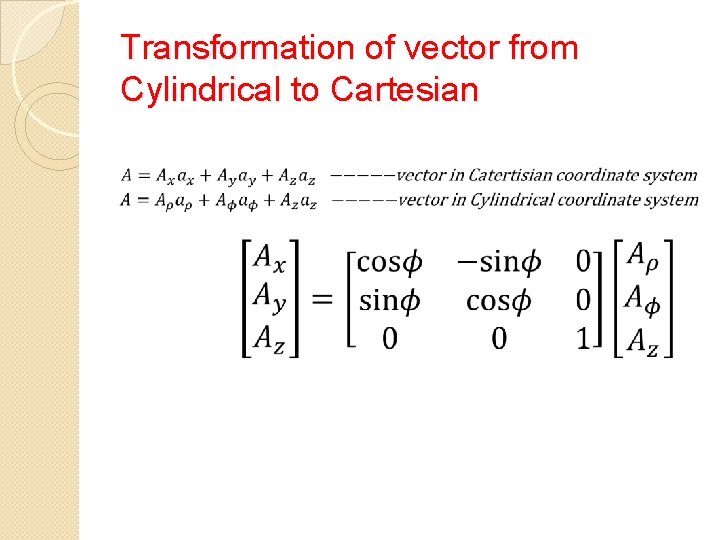
Transformation of vector from Cylindrical to Cartesian

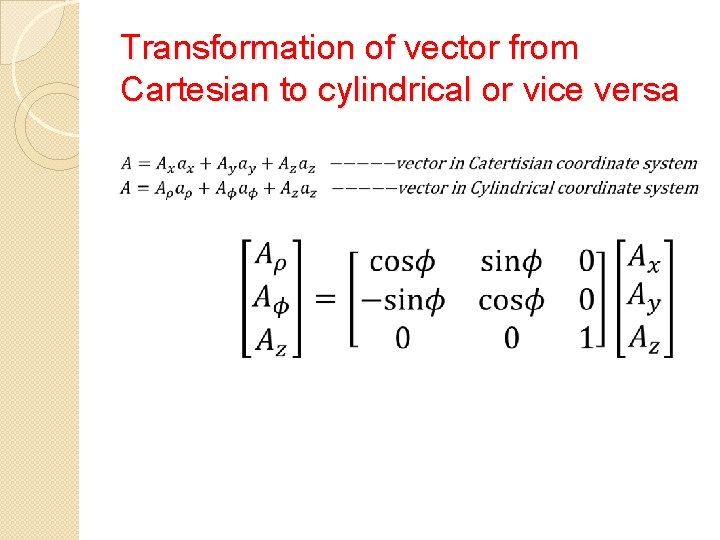
Transformation of vector from Cartesian to cylindrical or vice versa

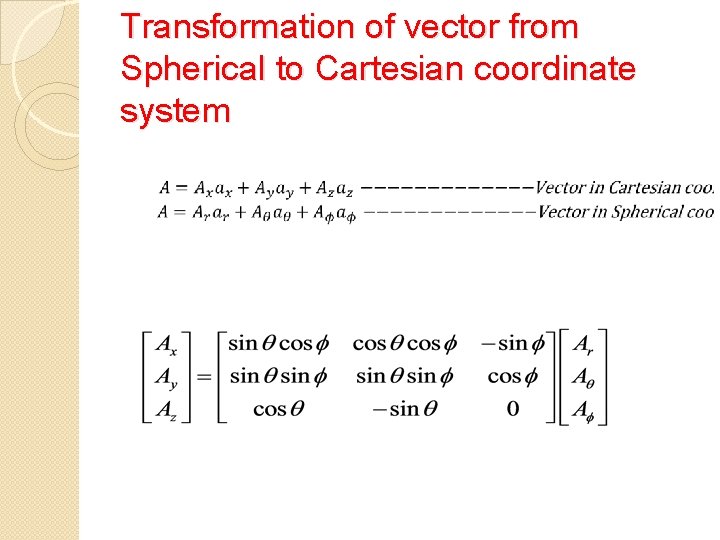
Transformation of vector from Spherical to Cartesian coordinate system

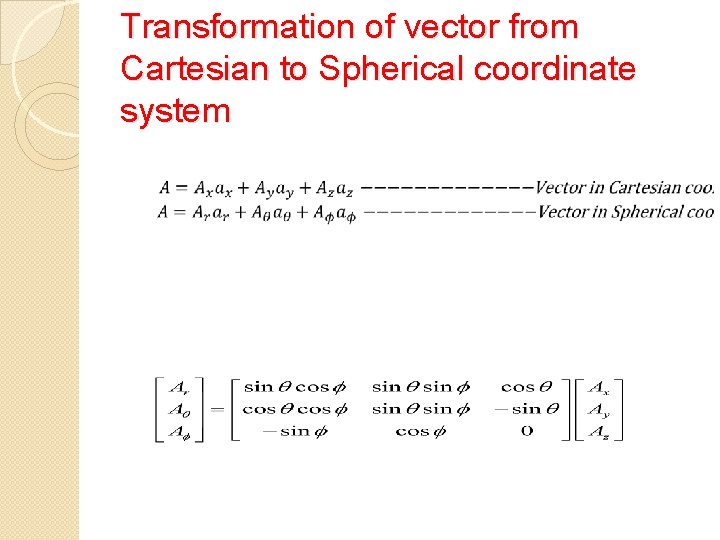
Transformation of vector from Cartesian to Spherical coordinate system

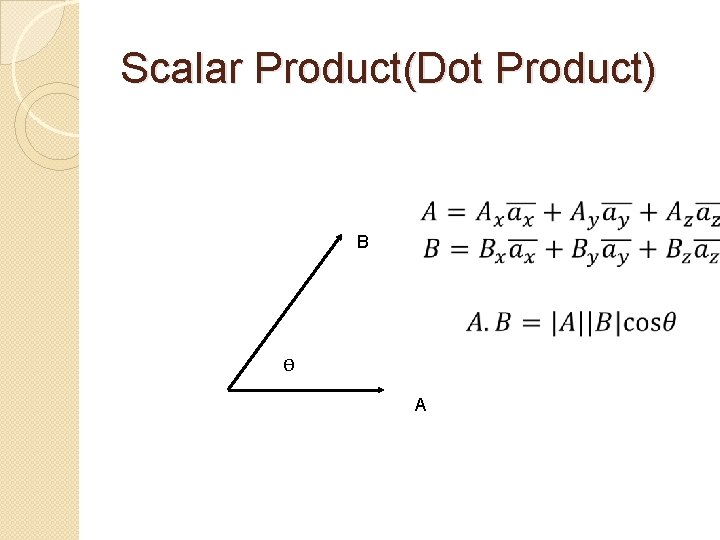
Scalar Product(Dot Product) B Ɵ A

Vector product(Cross product)

Divergence of vector in different coordinate system Cartesian Coordinate system Cylindrical Co-ordinates system Spherical Co-ordinates system


Divergence Theorem The volume integral of the divergence of vector field D taken over any volume V is equal to the surface integral of D taken over the closed surface enclosing the volume V

Curl

Gradient �V –Scalar field

Stoke’s theorem �It stats that integration of tangential component of vector field along the closed path is equal to integral of normal component of curl of the vector field over the surface enclosed by the closed path.

Line

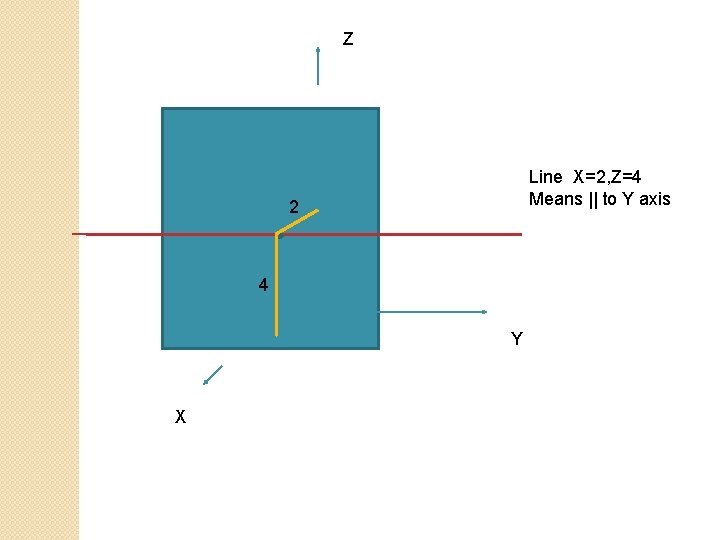
Z Line X=2, Z=4 Means || to Y axis 2 4 Y X

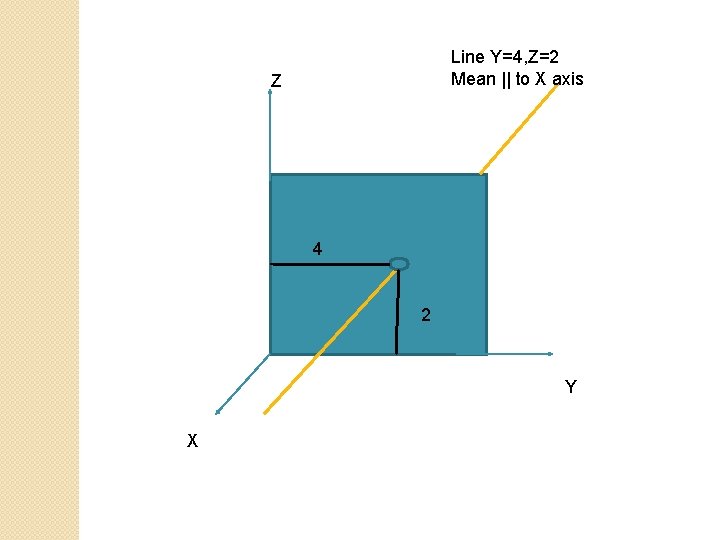
Line Y=4, Z=2 Mean || to X axis Z 4 2 Y X

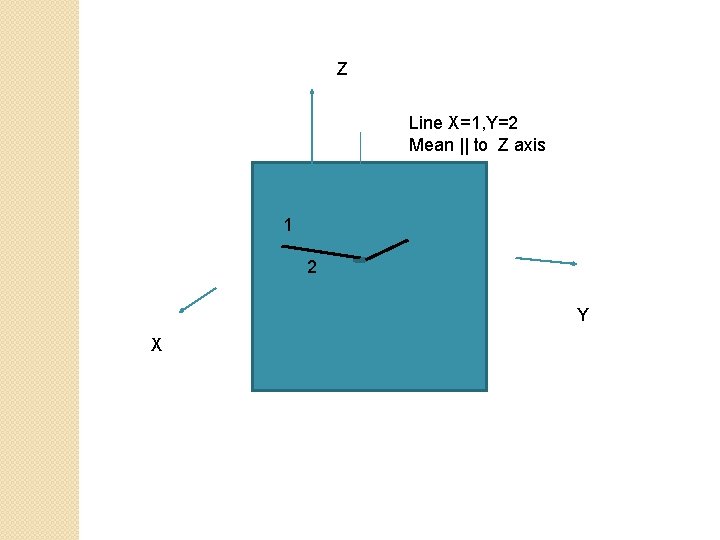
Z Line X=1, Y=2 Mean || to Z axis 1 2 Y X

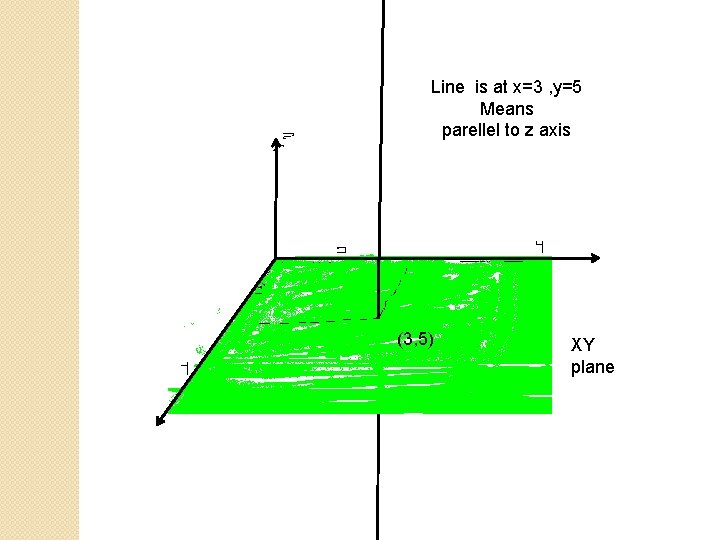
Line is at x=3 , y=5 Means parellel to z axis (3, 5) XY plane

Plane

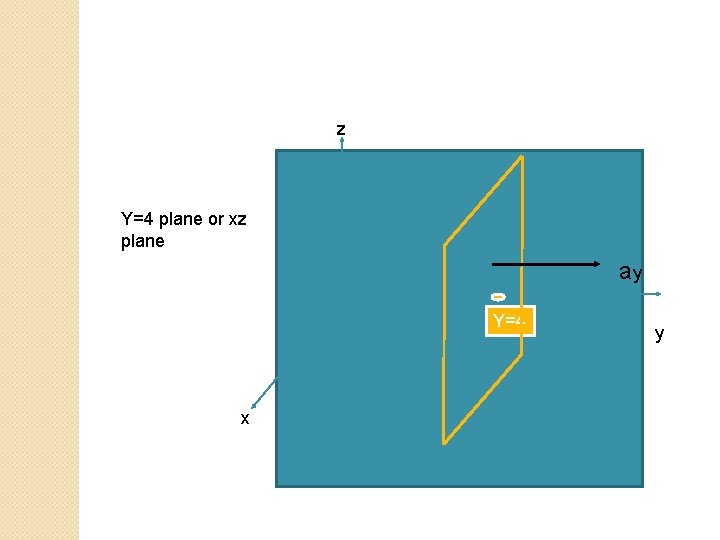
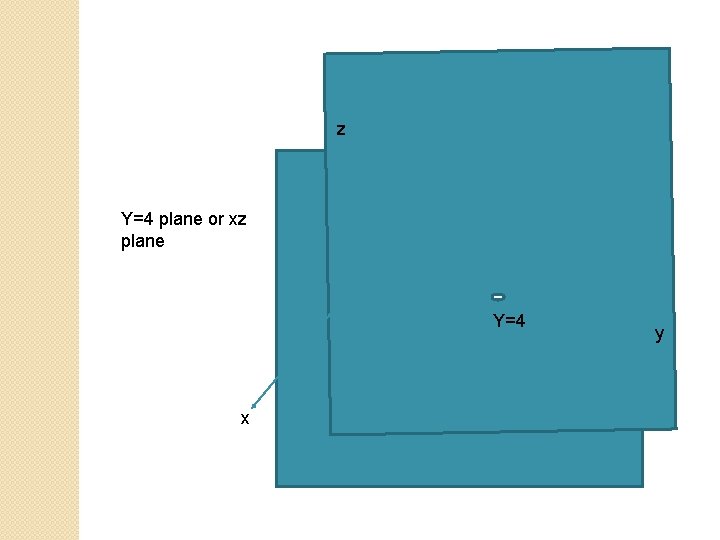
z Y=4 plane or xz plane ay Y=4 x y

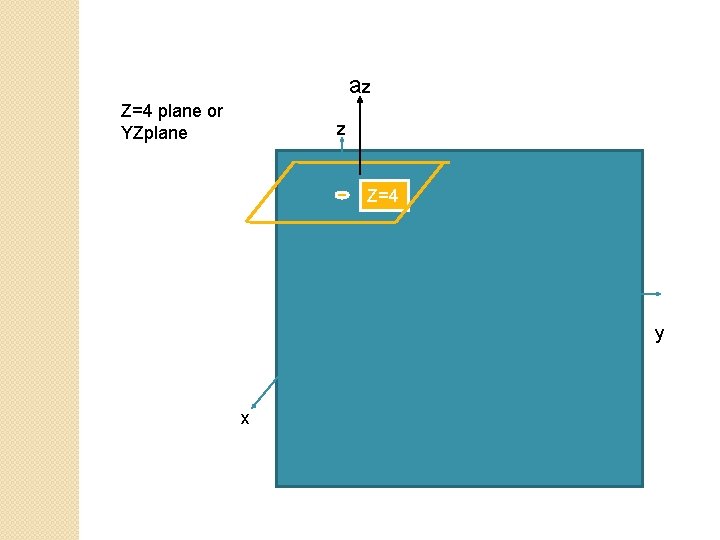
az Z=4 plane or YZplane z Z=4 y x

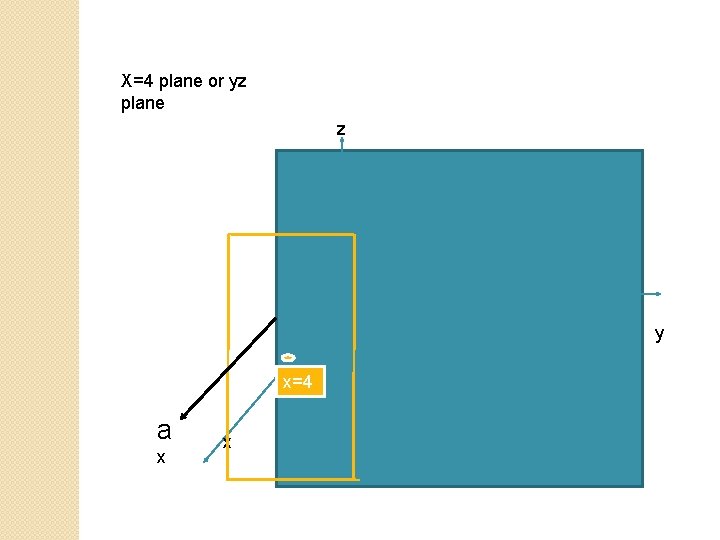
X=4 plane or yz plane z y x=4 a x x

z Y=4 plane or xz plane Y=4 x y
 The unforgettable history question and answer
The unforgettable history question and answer Coordinate direction angles
Coordinate direction angles Define position vector with example
Define position vector with example Cartesian vector
Cartesian vector What is rationalism
What is rationalism Mind body dualism descartes
Mind body dualism descartes Rectangular form
Rectangular form X axis quadrant
X axis quadrant Cartesian equations
Cartesian equations Draw this
Draw this Monism
Monism Cartesian product example
Cartesian product example Cartesian plane named after
Cartesian plane named after Cylindrical coordinate grapher
Cylindrical coordinate grapher Nested quantifiers
Nested quantifiers What is cartesian form
What is cartesian form Transformation from cartesian to spherical coordinates
Transformation from cartesian to spherical coordinates Cartesian plane activities
Cartesian plane activities Argand diagram argument
Argand diagram argument Fuzzy tolerance relation
Fuzzy tolerance relation Complex algebra and phasors
Complex algebra and phasors Unscented trajectory chapter 5
Unscented trajectory chapter 5 Cartesian product venn diagram
Cartesian product venn diagram Addition of cartesian vectors
Addition of cartesian vectors Cartesian product operation
Cartesian product operation Cartesian mind body dualism
Cartesian mind body dualism Cross join
Cross join Definition of power set
Definition of power set Cartesian method of doubt
Cartesian method of doubt Polar curves examples
Polar curves examples Disjoint sets
Disjoint sets Cartesian product example
Cartesian product example Cartesian product and relations
Cartesian product and relations Koordinat silinder
Koordinat silinder Complex numbers in cartesian form
Complex numbers in cartesian form Cartesian space vs joint space
Cartesian space vs joint space Contoh kalkulus relasional
Contoh kalkulus relasional Haskell operator precedence
Haskell operator precedence Cartesian vectors statics
Cartesian vectors statics Sistem koordinat cartesian
Sistem koordinat cartesian Cgvr
Cgvr Dot product properties
Dot product properties Proc sql cartesian product
Proc sql cartesian product Cartesian product
Cartesian product The new cartesian sign convention for spherical mirrors
The new cartesian sign convention for spherical mirrors Vector equation of line
Vector equation of line What is robot anatomy
What is robot anatomy クオリア問題
クオリア問題 Definition of power set
Definition of power set Cartesian trajectory
Cartesian trajectory Rectangular form of parametric equations
Rectangular form of parametric equations Converting polar coordinates to rectangular coordinates
Converting polar coordinates to rectangular coordinates Functionalism philosophy explained
Functionalism philosophy explained Cartesian form
Cartesian form Cr equation in polar form
Cr equation in polar form Directed line segment definition geometry
Directed line segment definition geometry Vector resultante
Vector resultante Vector resolution examples
Vector resolution examples Chapter review motion part a vocabulary review answer key
Chapter review motion part a vocabulary review answer key Uncontrollable spending ap gov
Uncontrollable spending ap gov Nader amin-salehi
Nader amin-salehi Traditional and systematic review venn diagram
Traditional and systematic review venn diagram Narrative review vs systematic review
Narrative review vs systematic review The analysis of ac circuits uses a rotating vector called a
The analysis of ac circuits uses a rotating vector called a Dot
Dot Review adalah
Review adalah Sentiment analysis for hotel reviews
Sentiment analysis for hotel reviews Swot analysis customer service example
Swot analysis customer service example Structured analysis process
Structured analysis process Static malware analysis vs dynamic malware analysis
Static malware analysis vs dynamic malware analysis Content meaning
Content meaning Difference between contrastive analysis and error analysis
Difference between contrastive analysis and error analysis Types of intralingual errors
Types of intralingual errors Types of fact gathering in system analysis and design
Types of fact gathering in system analysis and design Task analysis and content analysis
Task analysis and content analysis Transactions in transactional analysis
Transactions in transactional analysis Ssad vs ooad
Ssad vs ooad Lex
Lex Content analysis secondary data
Content analysis secondary data Feasibility in system analysis and design
Feasibility in system analysis and design Kmo test
Kmo test Ab
Ab Reciprocal lattice vector
Reciprocal lattice vector Poynting vector
Poynting vector Vector electrical engineering
Vector electrical engineering Standard unit vector
Standard unit vector Magnitude formula
Magnitude formula How to write component form of a vector
How to write component form of a vector Vector vs scalar
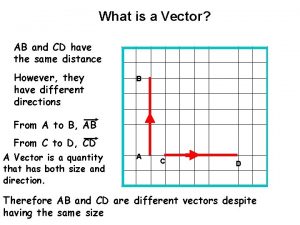
Vector vs scalar Vectors are quantities that have magnitude and
Vectors are quantities that have magnitude and What are vectors and scalars
What are vectors and scalars