Unit VII Logarithmic Functions Section VIIA Logarithmic Functions

Unit VII – Logarithmic Functions

Section VII-A: Logarithmic Functions • A logarithm is another way of writing a statement involving exponents. • A logarithm is equal to the exponent to which a specified base is raised to obtain a given value. • You can easily write an exponential equation as a logarithmic equation and vice versa.

EXAMPLE EXPONENTIAL FORM LOGARITHMIC FORM

EXAMPLE (cont. ) • Now, write each logarithmic equation in exponential form. • A logarithm with a base of 10 is known as a common logarithm. • Common logarithms are not written with a base.

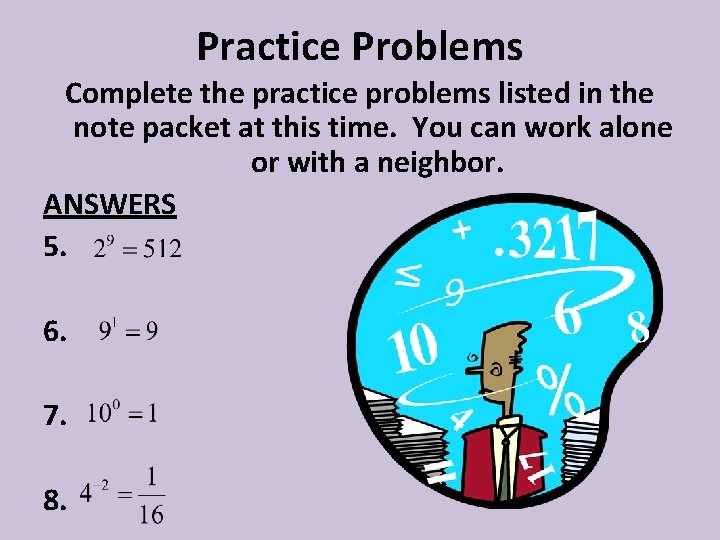
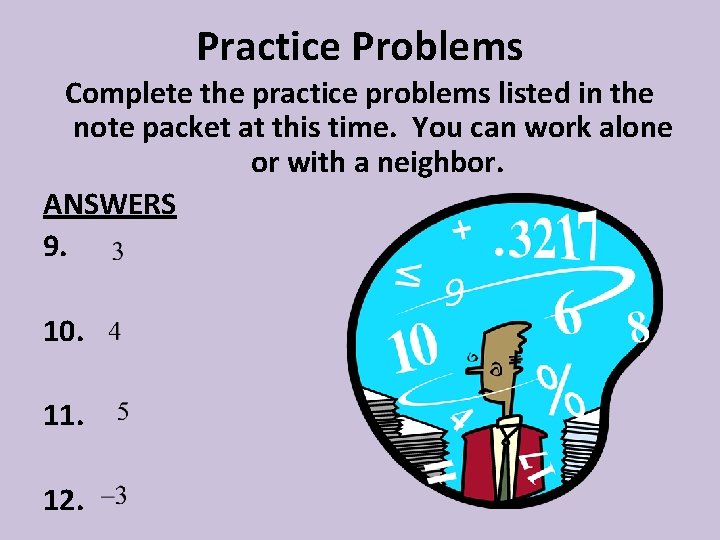
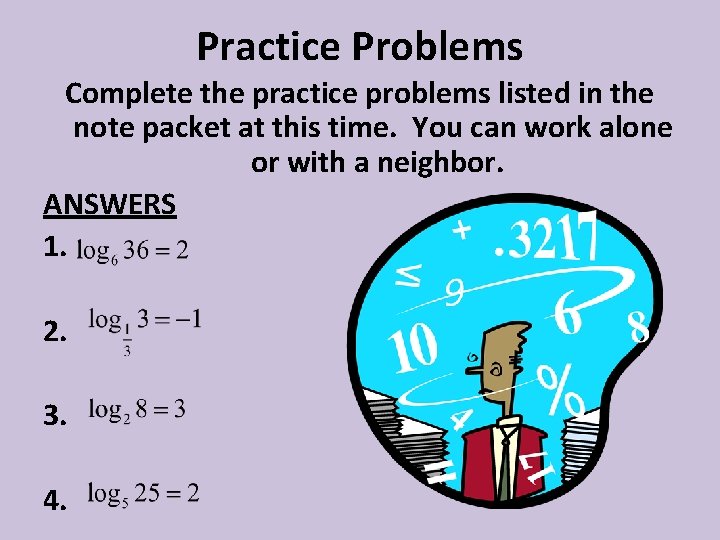
Practice Problems Write each exponential equation as a logarithmic equation. 1. 2. 3. 4. Write each logarithmic equation as an exponential equation. 5. 6. 8. Evaluate each. 9. 10. 11. 12. 7.

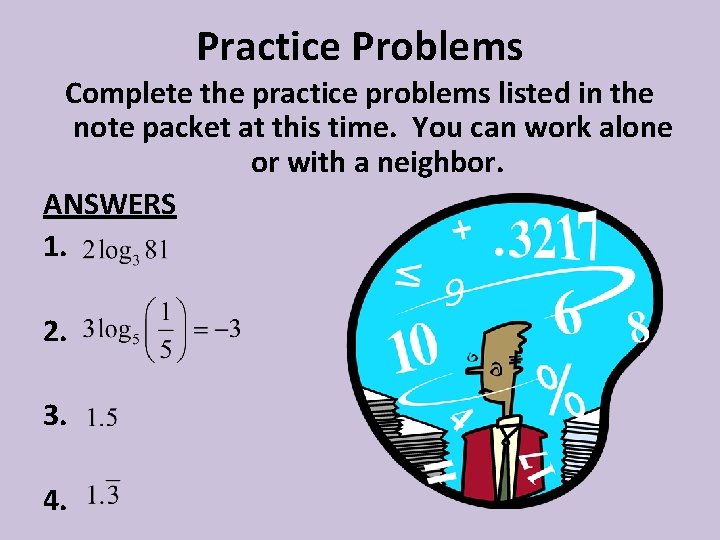
Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 1. 2. 3. 4.

Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 5. 6. 7. 8.

Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 9. 10. 11. 12.

HOMEWORK Complete problems on pg. 253 (#2 – 13; 17 – 28). This assignment will be due at the beginning of the next class session. 9

Section VII-B: Properties of Logarithms • Now that we know what logarithms are, we need to understand a little more about their general properties. • The Product Property of logarithms tells us that the logarithm of a product is equal to the sum of the logarithms of its factors.

EXAMPLE In other words, This is because we normally add exponents when we are multiplying.

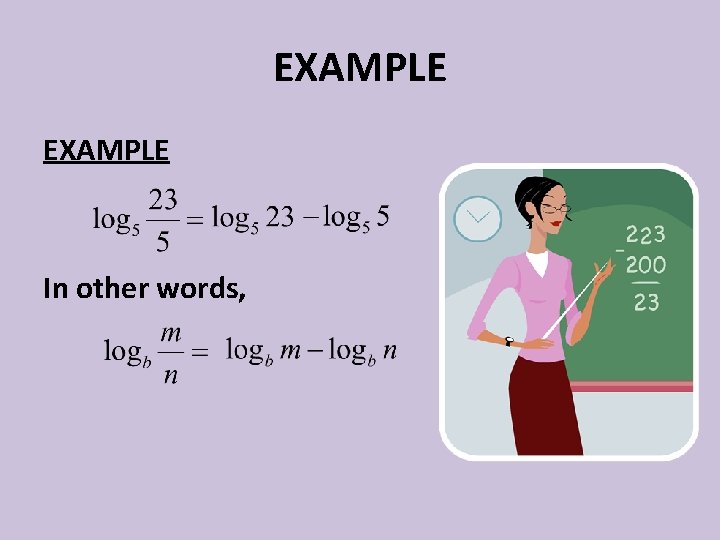
Division • When we are dividing, we usually subtract the exponents. • This leads us to the quotient property. • The quotient property tells us that the logarithm of a quotient is the logarithm of the dividend minus the logarithm of the divisor.

EXAMPLE In other words,

The Power Property • The power property of logarithms tells us that the logarithm of a power is the product of the exponent and the logarithm. EXAMPLE In other words,

Change of Base • Another important property is the change of base formula. • It allows us to change the base of any logarithm to any value we choose. • Since we have a common logarithm key on most calculators, we usually change the base to 10. CHANGE OF BASE FORMULA

EXAMPLE Evaluate using the change of base. • The change of base formula can be used to find the value of any logarithm. • If we change the base to 10 we can use the calculator to evaluate the common logarithms.

Practice Problems Express each as a single logarithm. Simplify if possible. 1. 2. 3. 4. Express each logarithm as a product. Simplify if possible. 5. 6. Evaluate each using the Change of Base Formula. 7. 8.

Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 1. 2. 3. 4.

Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 1. 2. 3. 4.

HOMEWORK Complete problems pg. 260 (#1 – 18; 20 – 31). This assignment will be due at the beginning of the next class session. 20

Section VII-C: Exponential and Logarithmic Equations • An exponential equation is any equation that contains a variable in one of the exponents. • To solve an exponential equation, we can do two things. Solving Exponential Equations 1. Write them so all of the bases are the same. 2. Take the common logarithm of both sides.

EXAMPLE Solve and Check. Remember to always check your answers!

EXAMPLE 2 Solve and Check.

Logarithmic Equations • A logarithmic equation is an equation with a logarithmic expression that contains a variable. • We can solve logarithmic equations by using the properties of logarithms. • In solving a logarithmic equation, we should try to reduce each side of the equation to a single logarithm. • Once this is done, make each side the exponent of the same base.

EXAMPLE 4 Solve and Check. Remember to always check your answers!

EXAMPLE 5 Solve and Check. Remember to always check your answers!

Practice Problems Solve and Check. 1. 2. 3. 4. 5. 6.

Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 1. 2. 3. 4. 5.

HOMEWORK Complete problems pg. 270 (#2 – 16; 21 – 33). This assignment will be due at the beginning of the next class session. 29

Section VII-D: The Natural Base, e • We often refer to e as the natural base. • Any logarithm with a base of e is referred to as a natural logarithm. • The natural logarithm button is also located on the calculator. (ln) • The natural logarithm is often used when we deal with exponential growth or decay. • The natural logarithm function can be used as the inverse of exponential functions with a base of e.

EXAMPLE Simplify.

Compounding Interest • We often use the base e when dealing with interest that is compounded continuously. FORMULA FOR CONTINUOUSLY COMPOUNDED INTEREST In this formula, A is the total value of the account, P is the principal, r is the annual interest rate, and t is time in years.

EXAMPLE What is the amount in an investment account that was opened with $1000 invested at 5% for 10 years compounded continuously?

Practice Problems Simplify. 1. 2. 3. Solve. 4. 5. 6. What is the total amount for an investment of $500 invested at 5. 25% interest for 40 years and compounded continuously?

Practice Problems Complete the practice problems listed in the note packet at this time. You can work alone or with a neighbor. ANSWERS 1. 2. 3. 4. 5.

HOMEWORK Complete problems pg. 278 (#6 – 11; 17 – 21; 31 – 36). This assignment will be due at the beginning of the next class session. 36