Unit V Code Optimization and Code Generation 1

Unit V – Code Optimization and Code Generation 1

Code Optimization - Introduction • It optimizes the three address codes into sequence of optimized three address codes. Intermediate Code Statements (Three Address Codes) Code Optimization Optimized Three Address Codes 2

Contd… • Properties of object Program: – Should occupy less memory space – Should run faster • Optimizing Compilers: – Compilers that apply code-improving transformations • Criteria for code – improving transformation: – Transformation - provides the meaning of programs i. e. , optimization must not change the output produced by a program. – Speed up the programs. 3

Contd… • Organization of an Optimizing Compiler: – This phase consists of control flow and data flow analysis followed by an application of transformations. FRONT END Control Flow Analysis CODE OPTIMIZER Data Flow Analysis CODE GENERATOR Transformations 4

Contd… • Advantages of this organization: – The operations needed to implement high-level constructs are made explicit in intermediate code, so it is possible to optimize them. – Intermediate code can be independent of the target machine, so the optimizer does not have to change much if the code generator is replaced by one for a different machine. 5

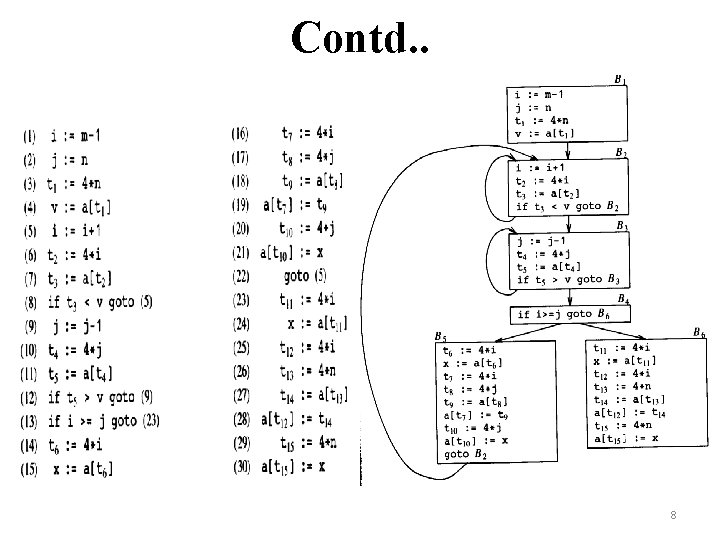
Basic Blocks • BB is a sequence of consecutive statements in which the flow control enters at the beginning and leaves at the end without halt or possible branching except at the end. • Algorithms for Partitioning the set of three address codes into Basic Blocks: – Input: A sequence of three address statements. – Output: A list of basic blocks with each three address statement in exactly one block. 6

Contd. . – Method: 1. First determine the set of leaders, the first statement of basic blocks. The rules to be used are: a. The first statement is a leader. b. Any statement which is the target of a conditional or unconditional goto is a leader. c. Any statement which immediately follows a conditional or unconditional goto is a leader. 2. For each construct its basic block, which consists of the leader and all statements up to but not including the next leader or the end of the program. 7

Contd. . 8

Contd… • Flow Graphs: – In this phase, programs are represented by Flow graphs. – Flow graph is a directed graph in which 1. Directed Edges indicate flow of control (execution) 2. Nodes indicate Basic Blocks 3. One node – Initial; it is the block whose leader is the first statement. 4. There is a directed edge from block B 1 to block B 2, if B 2 could follow B 1 during execution, i. e. , if a. There is a conditional or unconditional jump from the last statement of B 1 to the first statement of B 2 (or) b. B 2 immediately follows B 1 in the order of the program and B 1 does not end in an unconditional jump. 9

Principal Sources of Optimization • Code Optimization techniques consists of detecting patterns in the program and replacing these patterns by equivalent but more efficient constructs. • Types of Optimization: – Local optimization: within a basic block – Global optimization: otherwise – Mixed 10

Local Optimization • Otherwise known as Function-Preserving transformation. • Improving performance without changing function. • Techniques – – Common sub expression Elimination Copy Propagation Dead-code elimination Constant folding 11

Common sub expression Elimination • An occurrence of an expression E is common sub expression if E was previously computed and the values of variables in E have not changed since. • Example: Consider the following code, a = b * c + g; d = b * c * e; After process, the code becomes: tmp = b * c; a = tmp + g; d = tmp * e; 12

Copy Propagation • An idea behind this technique is to use g for f whenever possible after the copy of f : = g before After x : = t 3 x: = t 3 a[t 7]: =t 5 a[t 7] : = t 5 a[t 10] : = t 3 a[t 10] : = x Goto b 22 Goto b 2 13

Dead code elimination • A variable is live at a point in a program if its value can be used subsequently; otherwise it is dead at that point. • Remove unreachable code (Removes the code which does not affect the program results). 14

Contd… • In the example below, the value assigned to i is never used, and the dead store can be eliminated. The first assignment to global is dead, and the third assignment to global is unreachable; both can be eliminated. int global; void f () { int i; i = 1; /* dead store */ global = 2; return; global = 3; /* unreachable */ } After dead code elimination int global; void f () { global = 2; return; } 15

Constant Folding • Constant folding is the process of recognizing and evaluating constant expressions at compile time rather than computing them at runtime. • Expressions with constant operands can be evaluated at compile time, thus improving run-time performance and reducing code size by avoiding evaluation at compile-time. • Constant folding is a relatively easy optimization. 16

Contd… Example: • In the code fragment below, the expression (3 + 5) can be evaluated at compile time and replaced with the constant 8. int f (void) { return 3 + 5; } • Below is the code fragment after constant folding. int f (void) { return 8; } 17

Global Optimizations (Loop) • Otherwise known as Loop Optimizations. • Beyond basic block • Three important techniques – Code motion – Induction-variable elimination – Reduction in strength 18

Code motion • Move code outside the loop since there are potential many iterations • Look for expressions that yield the same result independent of the iterations. Before: • While ( I <= limit – 2) After applying Code Motion: • T = limit – 2 While ( I <= T) 19

Induction Variable Elimination • This will decrease the total number of instructions as well as speed up the loop. • A variable ‘x’ is called an induction variable of a loop if every time the variable x changes value, it is incremented or decremented by some constant. • When there are two or more induction variable in a loop, and if all of them but one can be eliminated , that process is known as induction variable elimination. 20

Contd… • Example: Consider the following code, int a[SIZE]; After induction variable elimination, int b[SIZE]; void f (void) { int i 1, i 2, i 3; for (i 1 = 0, i 2 = 0, i 3 = 0; i 1 < SIZE; i 1++) a[i 2++] = b[i 3++]; return; } int a[SIZE]; int b[SIZE]; void f (void) { int i 1; for (i 1 = 0; i 1 < SIZE; i 1++) a[i 1] = b[i 1]; return; } 21

Reduction in Strength • The replacement of an expensive operation by a cheaper one is known as reduction in strength. • Once, induction variables are determined, the instructions can be modified by changing the expensive operations like multiplication by additions or subtractions. This replacement is known as strength reduction. • It will speed up the object code. B 3: j=j-1 t 4 = 4 *j t 5 = a [ t 4] If t 5 > v goto B 3: j=j-1 t 4 = t 4 -4 t 5 = a [ t 4] If t 5 > v goto B 3 22

Other optimizations • • Optimizations for Basic blocks Reducible flow graph Global Data flow analysis Machine dependent Optimizations 23