UNIT IV Graphs Theory Contents Introduction to Graphs

UNIT IV Graphs Theory

Contents

Introduction to Graphs Definition: A graph is collection of points called vertices & collection of lines called edges each of which joins either a pair of points or single points to itself. Mathematically graph G is an ordered pair of (V, E) Each edge eij is associated with an ordered pair of vertices (Vi, Vj).

Introduction to Graphs For Example, In Fig. G has graph 4 vertices v 1 e 2 e 1 v 2 e 3 e 5 namely v 1, v 2, v 3, v 4& 7 edges e 4 v 3 Namely e 1, e 2, e 3, e 4, e 5, e 6, e 7 e 6 Then e 1=(v 1, v 2) Similarly for other Graph G edges. v 4 In short, we can represent G=(V, E) where V=(v 1, v 2, v 3, v 4) & E=(e 1, e 2, e 3, e 4, e 5, e 6, e 7 )

Self Loops & Parallel Edges Definition: If the end vertices Vi & Vj of any edge eij are same, then edge eij called as Self Loop. For Example, In graph G, the edge e 6 =(v 3, v 3) is self loop. Definition: If there are more than one edge is associated with given pair of vertices then those edge called as Parallel or Multiple edge. For Example, In graph G, e 4 & e 7 has (v 3, v 4) are called as Parallel edge.

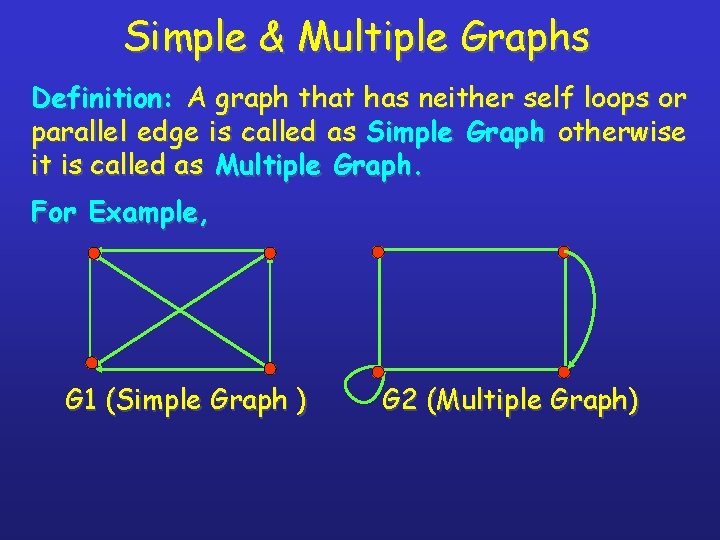
Simple & Multiple Graphs Definition: A graph that has neither self loops or parallel edge is called as Simple Graph otherwise it is called as Multiple Graph. For Example, G 1 (Simple Graph ) G 2 (Multiple Graph)

Weighted Graph Definition: If each edge or each vertex or both are associated with some +ve no. then the graph is called as Weighted Graph For Example, 1. 4 V 1 6 V 2 1. 5 V 4 1. 7 V 3

Finite & Infinite Graph Definition: A graph is Finite no. of vertices as well as finite no. of edges called as Finite Graph otherwise it is Infinite Graph. For Example, The graph G 1 & G 2 is Finite Graph. Definition: A graph G=(V, E) is called as Labeled Graph if its edges are labeled with some names or data. For Example, Graph G is labeled graph.

Adjacency & Incidence Definition: Two vertices v 1 & v 2 vertices of G joins directly by at least one edge then there vertices called Adjacent Vertices. For Example, In Graph G, v 1 & v 2 are adjacent vertices. Definition: If Vi is end vertex of edge eij=(vi, vj) then edge eij is said to be Incident on vi. Similarly eij is said to be Incident on vj. For Example, In Graph G, e 1 is incident on v 1 & v 2.

Degree of a Vertex Definition: The no. of edges incident on a vertex vi with self loop counted twice is called as degree of vertex vi. For Example, Consider the Graph G, d(v 1)=3 v 1 e 1 , d(v 2)=2 , d(v 3)=5 , d(v 4)= 4 e 2 v 4 e 3 e 5 e 4 v 3 e 7 Definition : e 6 A vertex with degree zero is called as Isolated Vertex & A vertex with degree one is called as Pendant Vertex.

Handshaking Lemma n i=1

Matrix Representation of Graphs A graph can also be represented by matrix. Two ways are used for matrix representation of graph are given as follows, 1. Adjacent Matrix 2. Incident Matrix Lets see one by one…

1. Adjacent Matrix The A. M. of Graph G with n vertices & no parallel edges is a symmetric binary matrix A(G)=[aij] or order n*n where, aij=1, if there is as edge between vi &vj. aij=0, if vi & vj are not adjacent. A self loop at vertex vi corresponds to aij=1. For Example, A(G)=

1. Adjacent Matrix The A. M. of multigraph G with n vertices is an n*n matrix A(G)=[aij] where, aij=N, if there one or more edge are there between vi &vj & N is no. of edges between vi & vj. aij=0, otherwise. For Example, A(G)=

2. Incident Matrix Given a graph G with n vertices , e edges & no self loops. The incidence matrix x(G)=[Xij] of the other graph G is an n*e matrix where, Xij=1, if jth edge ej is incident on ith vertex vi, Xij=0, otherwise. Here n vertices are rows & e edges are columns. X(G)=

Directed Graph or Diagraph Definition: If each edge of the graph G has a direction then graph called as diagraph. In a graph with directed edges, the in-degree of a vertex v, denoted by deg -(v) & out-degree of v, denoted by deg +(v). See the example in Next page….

Directed Graph or Diagraph Example: What are the in-degrees and out-degrees of the vertices a, b, c, d in this graph: deg-(a) = 1 deg+(a) = 2 deg-(d) = 2 deg+(d) = 1 a d b c deg-(b) = 4 deg+(b) = 2 deg-(c) = 0 deg+(c) = 2

Adjacency Matrix of a diagraph It is defined in similar fashion as it defined for undirected graph. For Example, A(D)=

Incident matrix of diagraph Given a graph G with n, e & no self loops is matrix x(G)=[Xij] or order n*e where n vertices are rows & e edges are columns such that, Xij=1, if jth edge ej is incident out ith vertex vi Xij=-1, if jth edge ej is incident into ith vertex vi Xij=0, if jth edge ej not incident on ith vertex vi.

Null Graph Definition: If the edge set of any graph with n vertices is an empty set, then the graph is known as null graph. It is denoted by Nn For Example, N 3 N 4

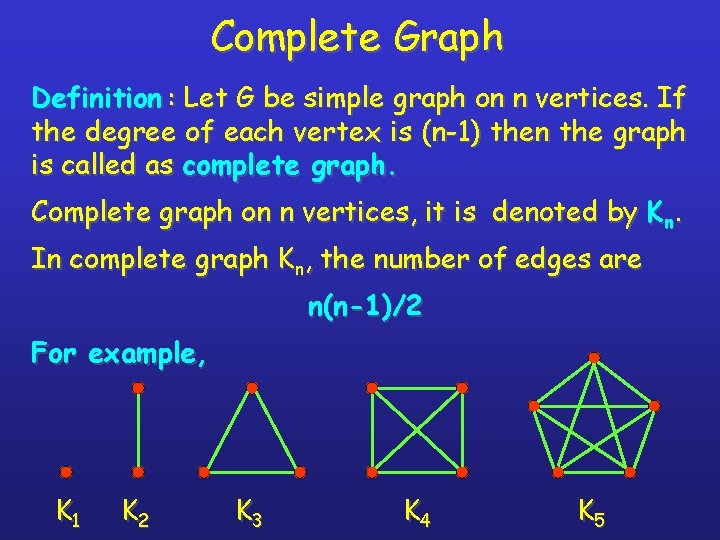
Complete Graph Definition : Let G be simple graph on n vertices. If the degree of each vertex is (n-1) then the graph is called as complete graph. Complete graph on n vertices, it is denoted by Kn. In complete graph Kn, the number of edges are n(n-1)/2 For example, K 1 K 2 K 3 K 4 K 5

Regular Graph Definition : If the degree of each vertex is same say ‘r’ in any graph G then the graph is said to be a regular graph of degree r. For example, K 3 K 4 K 5

Bipartite Graph

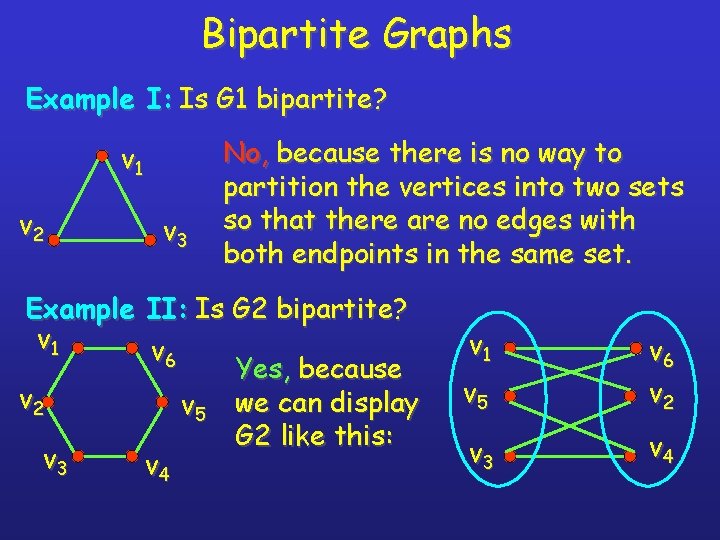
Bipartite Graphs Example I: Is G 1 bipartite? v 1 v 2 v 3 No, because there is no way to partition the vertices into two sets so that there are no edges with both endpoints in the same set. Example II: Is G 2 bipartite? v 1 v 6 Yes, because v 2 v 5 we can display G 2 like this: v 3 v 4 v 1 v 5 v 6 v 2 v 3 v 4

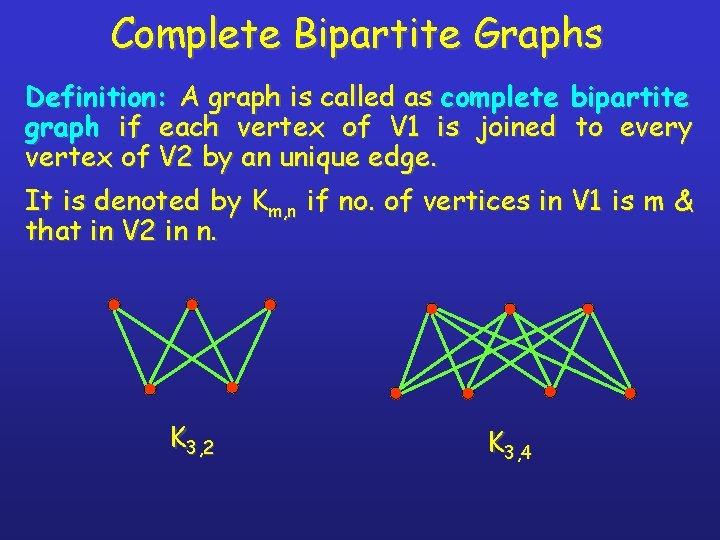
Complete Bipartite Graphs Definition: A graph is called as complete bipartite graph if each vertex of V 1 is joined to every vertex of V 2 by an unique edge. It is denoted by Km, n if no. of vertices in V 1 is m & that in V 2 in n. K 3, 2 K 3, 4

Linked representation of graphs a d b c Adjacent Vertex Vertices a b, c, d b a, d c a, d d a, b, c The above adjacency can be represented by, G=[a: b, c, d; b: a, d; c: a, d; d: a, b, c] This is link representation of the graph G.

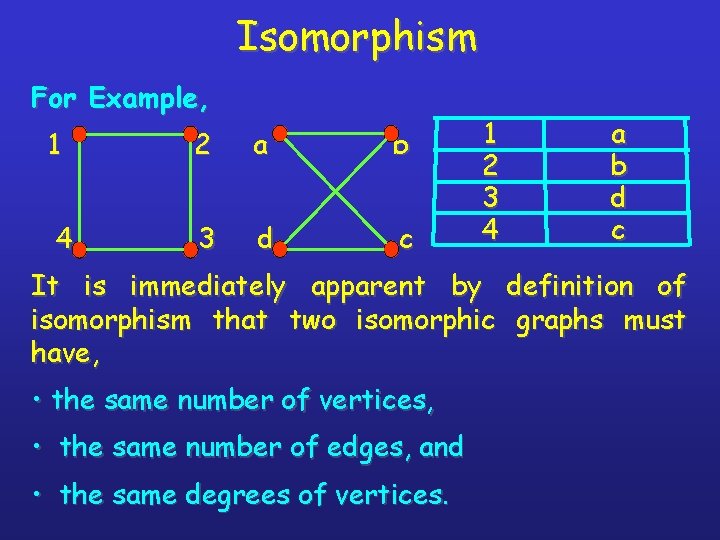
Isomorphism Definition : Two graphs are thought of as equivalent (called isomorphic ) if they have identical behavior in terms of graph theoretic properties. Two graphs G(V, E) & G’(V’, E’) are said to be isomorphic to each other if there is one-one correspondence between their vertices & between their edges such that incidence relationship in preserved. It is denoted by G 1=G 2

Isomorphism For Example, 1 2 a b 4 3 d c 1 2 3 4 a b d c It is immediately apparent by definition of isomorphism that two isomorphic graphs must have, • the same number of vertices, • the same number of edges, and • the same degrees of vertices.

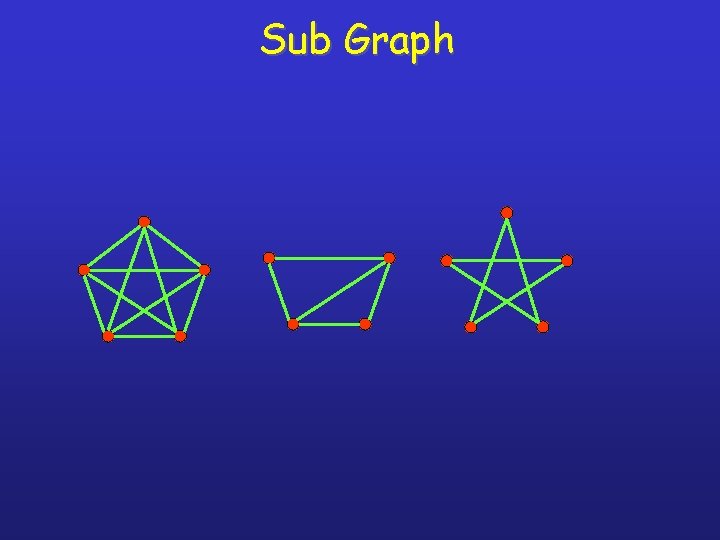
Sub Graph

Null Sub Graph Definition: A subgraph is called as null sub graph if its vertex set is same as vertex set of G & its edge set is empty set. i. e. it does not contain any edges. For Example: G Null Subgraph

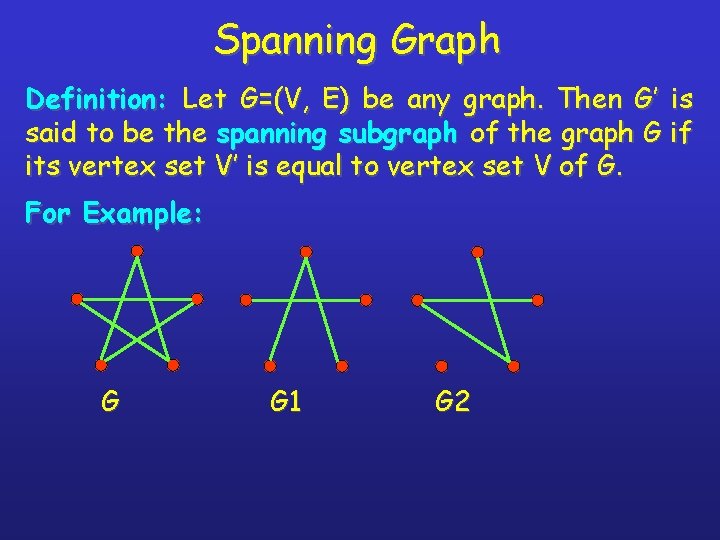
Spanning Graph Definition: Let G=(V, E) be any graph. Then G’ is said to be the spanning subgraph of the graph G if its vertex set V’ is equal to vertex set V of G. For Example: G G 1 G 2

Complement of a Graph Definition: Let G is a simple graph. Then complement of G denoted by ~G is graph whose vertex set is same as vertex set of G & in which two vertices are adjacent if & only if they are not adjacent in G. For Example: G ~G H ~H

Operations on Graphs G 1 G 2

Operations on Graphs G 1 G 2

Operations on Graphs G 1 G 2

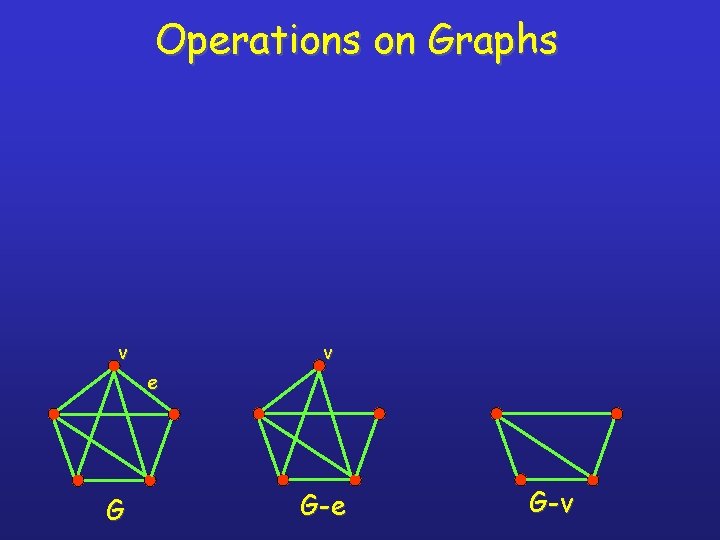
Operations on Graphs v v e G G-e G-v

Paths Definition: Path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. Definition: Path P of length n from v 0 to vn is a sequence of vertices & edges of form (v 0, e 1, v 1, e 2, …. , en, vn) where each ej is an edge between vj-1 & vj. The vertices v 0 & vn are called end points of path & the other vertices v 1…. , vn-1 are called its interior vertices. See the example in next page……

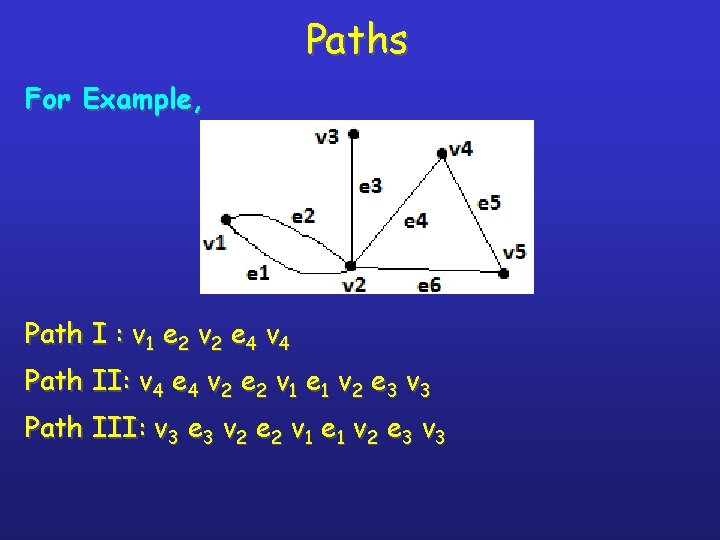
Paths For Example, Path I : v 1 e 2 v 2 e 4 v 4 Path II: v 4 e 4 v 2 e 2 v 1 e 1 v 2 e 3 v 3 Path III: v 3 e 3 v 2 e 2 v 1 e 1 v 2 e 3 v 3

Types of Paths 1. Simple Path: A path in a graph G is called as simple path if the edges do not repeat in the path. In Fig. path I & path II are simple graph but path III is not. 2. Elementary Path: A path is said to be elementary path if vertices do not repeat in the path. In Fig. path I is an elementary path but path II is not.

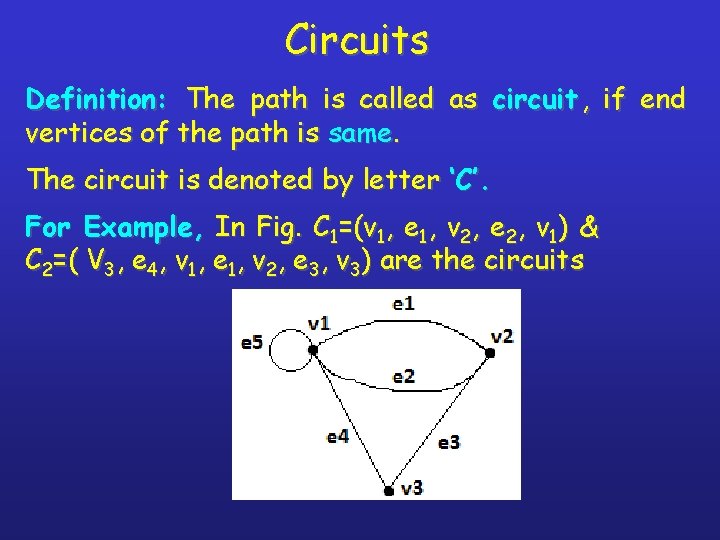
Circuits Definition: The path is called as circuit , if end vertices of the path is same. The circuit is denoted by letter ‘C’. For Example, In Fig. C 1=(v 1, e 1, v 2, e 2, v 1) & C 2=( V 3, e 4, v 1, e 1, v 2, e 3, v 3) are the circuits

Types of Circuits 1. Simple Circuit: A circuit in the graph G is said to be a simple circuit if is does not include the same edge twice. 2. Elementary Circuit: A circuit is said to be elementary circuit if it does not meet same vertex twice ( Except first & last vertex.

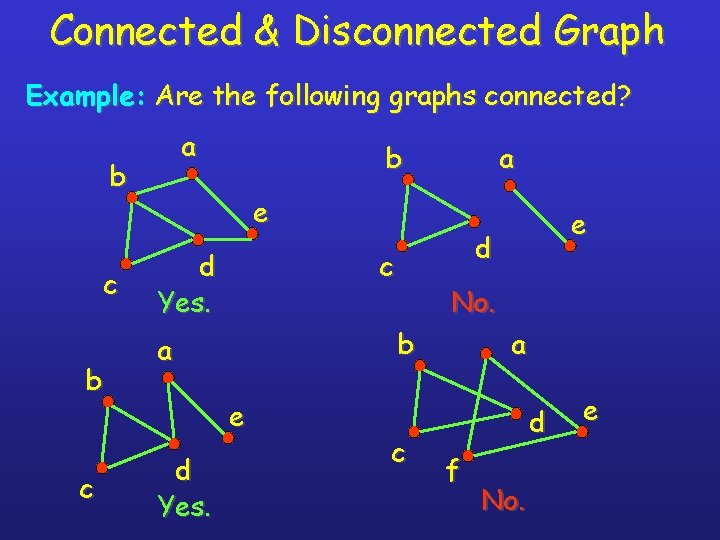
Connected & Disconnected Graphs Definition: A graph is said to be connected graph if there is exists the path between every pair of vertices, otherwise it is disconnected. See the example in next page….

Connected & Disconnected Graph Example: Are the following graphs connected? a b c b a e d Yes. No. b e d Yes. d c a e c a d f No. e

Connectivity In this section, we will see how the removal of edges & vertices disconnects the graph. For that we will see the concepts as given below, 1. Edge Connectivity 2. Vertex Connectivity Lets see one by one ……

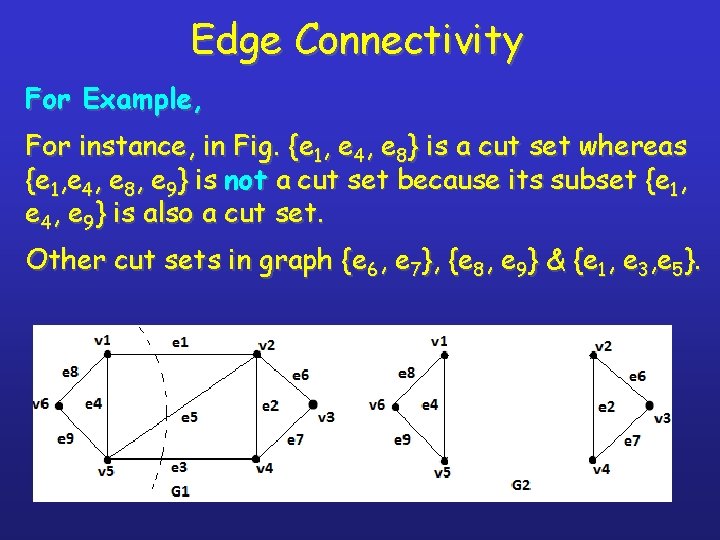
Edge Connectivity In Connected graph G, a cut set is a minimal set of edges whose removal disconnects the graph & increases the components of graph by one. The number of edges in a smallest cut set of a connected graph G is called as edge connectivity. It is denoted by λ (G). In other words, λ (G) is a smallest no. of edges in G whose removal disconnects G. See the example in Next Page…. .

Edge Connectivity For Example, For instance, in Fig. {e 1, e 4, e 8} is a cut set whereas {e 1, e 4, e 8, e 9} is not a cut set because its subset {e 1, e 4, e 9} is also a cut set. Other cut sets in graph {e 6, e 7}, {e 8, e 9} & {e 1, e 3, e 5}.

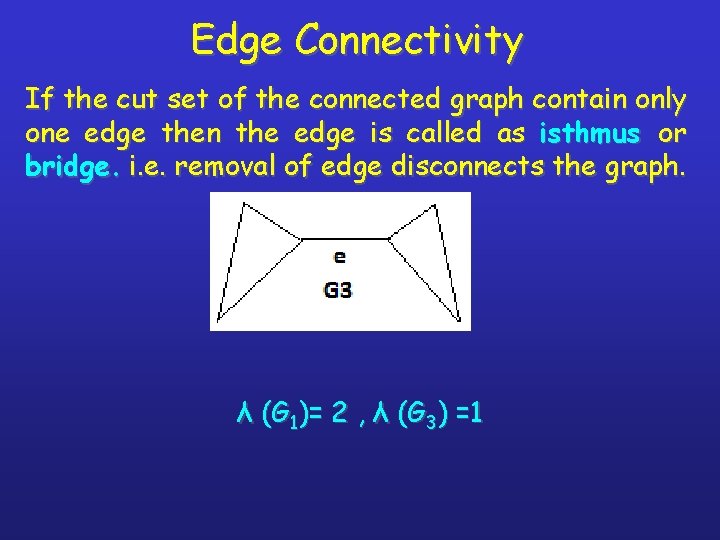
Edge Connectivity If the cut set of the connected graph contain only one edge then the edge is called as isthmus or bridge. i. e. removal of edge disconnects the graph. λ (G 1)= 2 , λ (G 3) =1

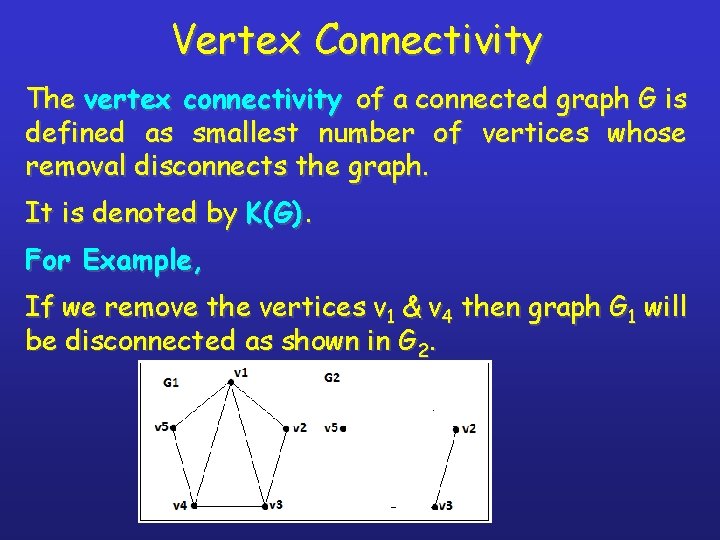
Vertex Connectivity The vertex connectivity of a connected graph G is defined as smallest number of vertices whose removal disconnects the graph. It is denoted by K(G). For Example, If we remove the vertices v 1 & v 4 then graph G 1 will be disconnected as shown in G 2.

Vertex Connectivity A graph is said to be separable graph if its vertex connectivity is one. Is separable graph, a vertex whose removal disconnects the graph is said to be a cut vertex or cut point. For Example, In this graph, the v is cut point.

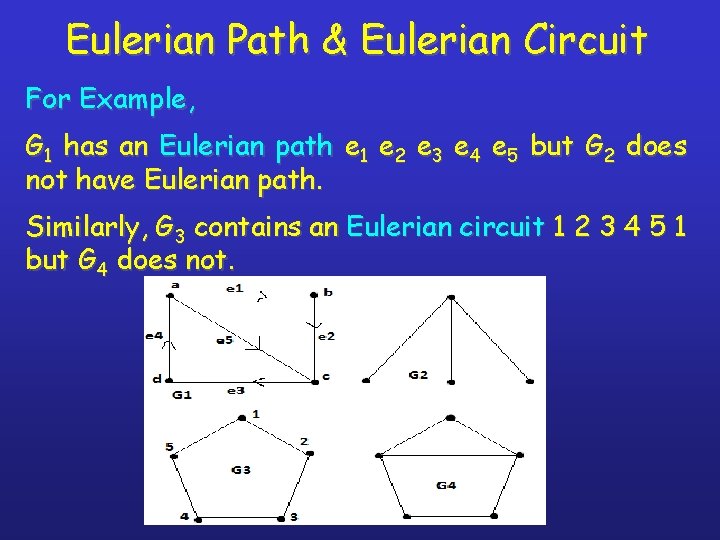
Eulerian Path & Eulerian Circuit A path is called as Eulerian Path if every edge in the graph G appears exactly once in the path. A circuit which contains every edge of the graph G exactly once is called as Eulerian Circuit. A graph which has an Eulerian circuit is called as Eulerian Graph. See the Example in next page…

Eulerian Path & Eulerian Circuit For Example, G 1 has an Eulerian path e 1 e 2 e 3 e 4 e 5 but G 2 does not have Eulerian path. Similarly, G 3 contains an Eulerian circuit 1 2 3 4 5 1 but G 4 does not.

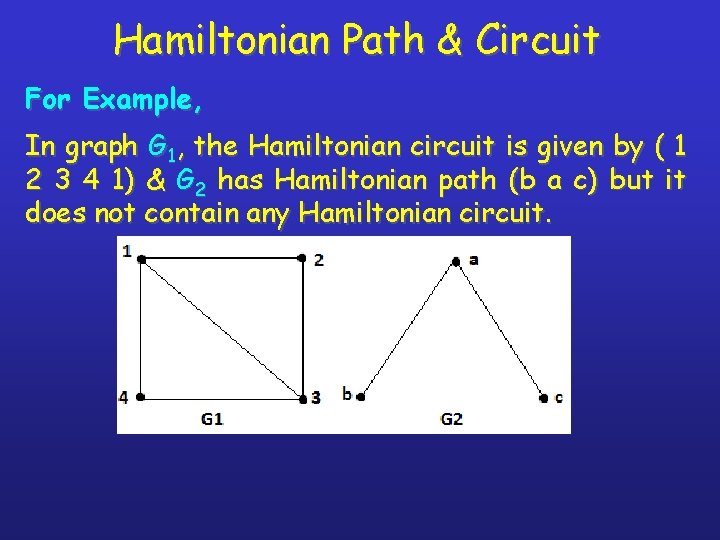
Hamiltonian Path & Circuit A path in a connected graph G is called as Hamiltonian Path if it contains every vertex of G exactly once. A circuit in a connected graph G is called Hamiltonian Circuit if it contains every vertex of G exactly once (Except first & last vertex). A graph which has Hamiltonian circuit is called as Hamiltonian Path. See the Example in next page…

Hamiltonian Path & Circuit For Example, In graph G 1, the Hamiltonian circuit is given by ( 1 2 3 4 1) & G 2 has Hamiltonian path (b a c) but it does not contain any Hamiltonian circuit.

Shortest Path Problem For Example, Given railway network connecting several cities, it is required to find shortest route between two cities. Pune 650 700 Mumbai 600 Nagpur 200 Nasik

Shortest Path Problem We now give an algorithm for solving the shortest path problem. The algorithm was found by Dijkstra in 1959 & is known as Dijkstra’s shortest path problem. This algorithm Gives shortest length of path from vertex ‘a’ to vertex ‘z’.

Dijkstra’s Algorithm

Dijkstra’s Algorithm Step 3: If v!=z, then revise labels of vertices of T. i. e. vertices which do not have permanent labels. The new label of vertex x in T is given by, L(x)= min {old L(x), L(v)+w (v, x)} Where w(v, x) is weight of edge joining vertex v & x. If there is no direct edge joining v & x then take w(v, x)= ∞. Step 4: Repeat steps 2 & 3 until z gets permanent label.

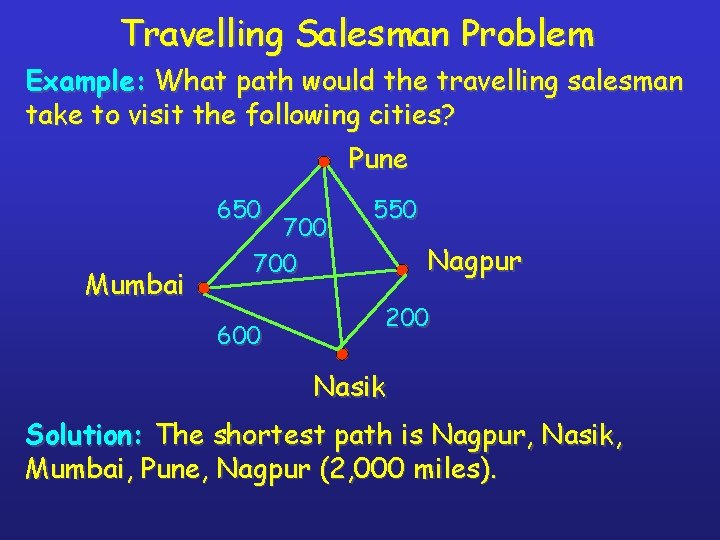
Travelling Salesman Problem The travelling salesman problem is one of the classical problems in computer science. A travelling salesman wants to visit a number of cities and then return to his starting point. Of course he wants to save time and energy, so he wants to determine the shortest path for his trip. We can represent the cities and the distances between them by a weighted, complete, undirected graph. The problem then is to find the circuit of minimum total weight that visits each vertex exactly one.

Travelling Salesman Problem Example: What path would the travelling salesman take to visit the following cities? Pune 650 Mumbai 700 600 550 Nagpur 200 Nasik Solution: The shortest path is Nagpur, Nasik, Mumbai, Pune, Nagpur (2, 000 miles).

Nearest Neighbour Method So efficient method is available to find the solution of travelling salesman problem. So method is Nearest Neighbour method which gives good results by travelling salesman problem. In this method, we start the H. Circuit with any vertex & find vertex which is nearest to it. Containing this way & coming back to starting vertex by travelling through all the vertices exactly once, we get the H. Circuit.

Nearest Neighbour Method This method is described below, 1. Start with any vertex (say v 1) & choose the vertex closest to starting vertex to form an initial path of one edge. Construct this path by selecting different vertices as described in step (2). 2. Let vn denote the latest vertex that was added to the path. Select vertex vn+1 closest to vn from all vertices that are not in the path & add this vertex to the path. 3. Repeat step (2) till all vertices of the graph G are included in the path. 4. Lastly form a circuit by adding the edge connecting the starting vertex & last vertex added.

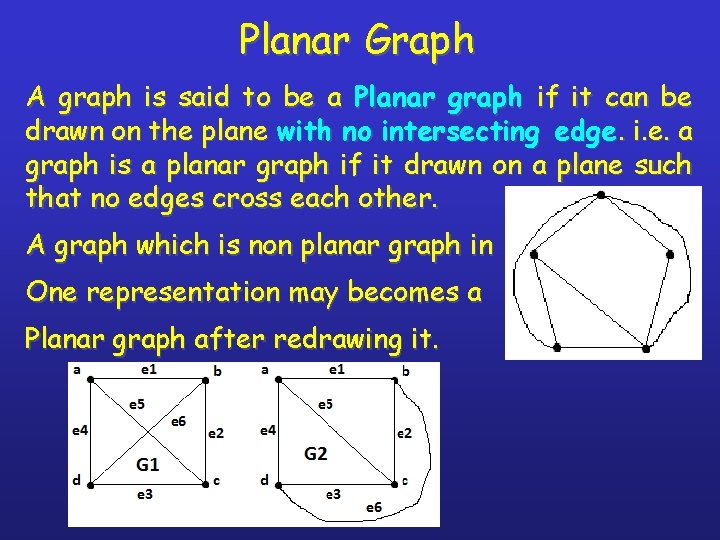
Planar Graph A graph is said to be a Planar graph if it can be drawn on the plane with no intersecting edge. i. e. a graph is a planar graph if it drawn on a plane such that no edges cross each other. A graph which is non planar graph in One representation may becomes a Planar graph after redrawing it.

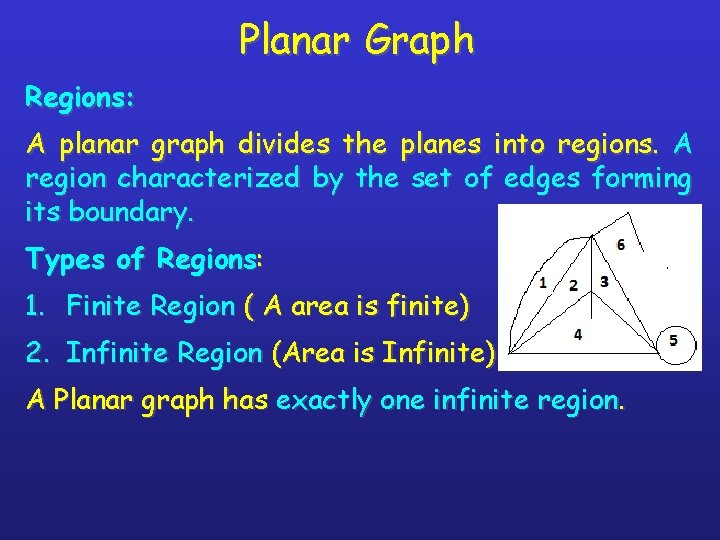
Planar Graph Regions: A planar graph divides the planes into regions. A region characterized by the set of edges forming its boundary. Types of Regions: 1. Finite Region ( A area is finite) 2. Infinite Region (Area is Infinite) A Planar graph has exactly one infinite region.

Planar Graph Euler’s Formula: The no. of regions in any planar representation depends upon no. of vertices & no. of edges in graph. The relation between edges, vertices & regions of any graph is given by Euler’s Formula. For any connected graph, v - e + r = 2 Where v, e, r the total no. of vertices, edges & regions in graph resp.

Planar Graph For Example, Here, v = 12 & e=15 then find r=? Acc. To Euler’s Formula, v-e-+r=2 r= 2 -v+e r= 2 -12+15 r= 5 So the graph G contains 5 Regions

The End