UNIT IV Beam Deflection Outline Deflection diagrams the

UNIT - IV Beam Deflection

Outline • • • Deflection diagrams & the elastic curve Elastic-beam theory The double integration method Moment-area theorems Conjugate-beam method 1

Deflection diagrams & the elastic curve • Deflections of structures can come from loads, temperature, fabrication errors or settlement. • In designs, deflections must be limited in order to prevent cracking of attached brittle materials. • A structure must not vibrate or deflect severely for the comfort of occupants. • Deflections at specified points must be determined if one is to analyze statically indeterminate structures. 2

• In this topic, only linear elastic material response is considered. • This means a structure subjected to load will return to its original undeformed position after the load is removed. • It is useful to sketch the shape of the structure when it is loaded in order to visualize the computed results & to partially check the results. 3

• This deflection diagram rep the elastic curve for the points at the centroids of the cross-sectional areas along each of the members. • Table 8. 1 shows the deflection at some typical joints. • If the elastic curve seems difficult to establish, it is suggested that the moment diagram be drawn first. • From there, the curve can be constructed. 4

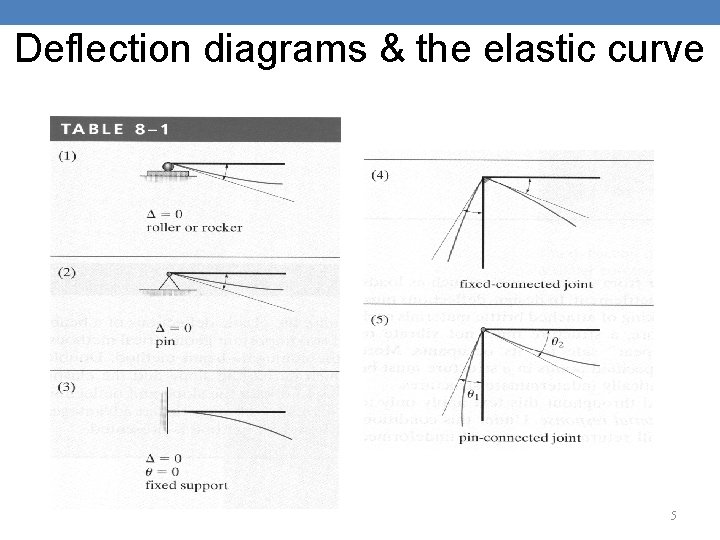
Deflection diagrams & the elastic curve 5

3 -1 Deflection diagrams & the elastic curve • Consider the beam in Fig 8. 3 • Due to pin-and-roller support, the displacement at A & D must be zero. • Within the region of –ve moment, the elastic curve is concave downward. • Within the region of +ve moment, the elastic curve is concave upward. • There must be an inflection point where the curve changes from concave down to concave up. 6

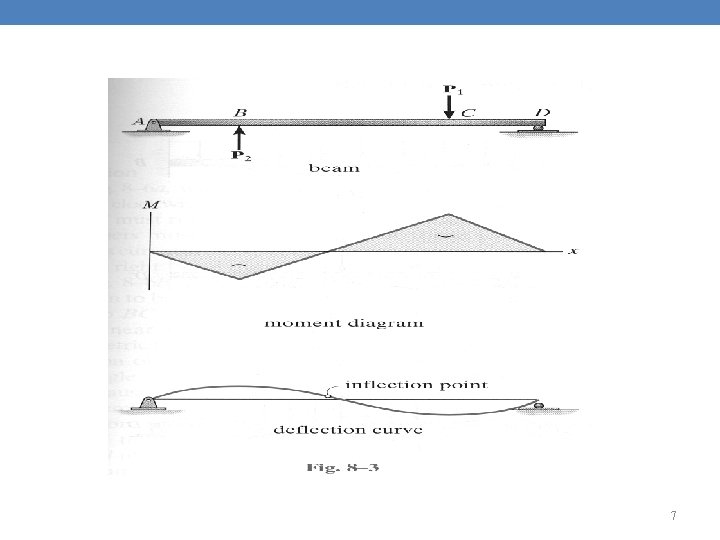
7

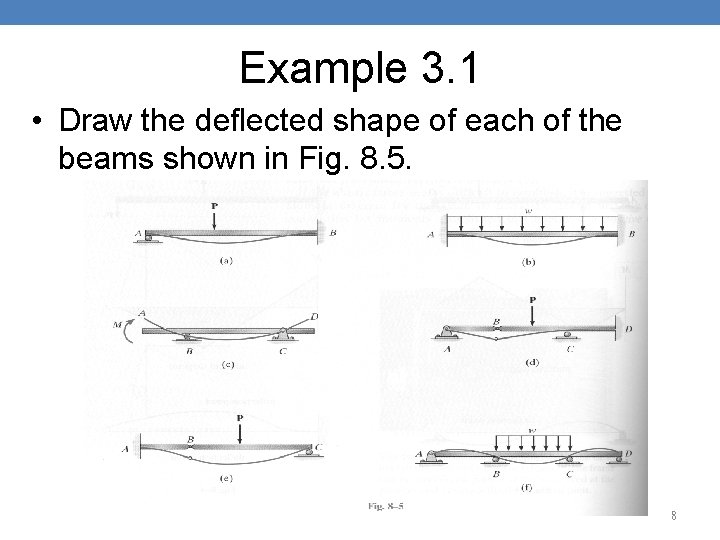
Example 3. 1 • Draw the deflected shape of each of the beams shown in Fig. 8. 5. 8

Example 3. 1 - solution • In Fig 8. 5(a), the roller at A allows free rotation with no deflection while the fixed wall at B prevents both rotation and deflection. • The deflected shape is shown by the bold line. • In Fig. 8. 5(b), no rotation or deflection occur at A & B. • In Fig. 8. 5(c), the couple moment will rotate end A. • This will cause deflections at both ends of the beam since no deflection is possible at B & C. 9

Example 3. 1 - solution • Notice that segment CD remains undeformed since no internal load acts within. • In Fig. 8. 5(d), the pin at B allows rotation, so the slope of the deflection curve will suddenly. change at this point while the beam is constrained by its support. • In Fig. 8. 5(e), the compound beam deflects as shown. • The slope changes abruptly on each side of B. 10

Example 3. 1 - solution • In Fig. 8. 5(f), span BC will deflect concave upwards due to load. • Since the beam is continuous, the end spans will deflect concave downwards. 11

Elastic Beam theory • To derive the DE, we look at an initially straight beam that is elastically deformed by loads applied perpendicular to beam’s x-axis & lying in x-v plane of symmetry as shown in Fig. 8. 7(a). • Due to loading, the beam deforms under shear & bending. • If beam L >> d, greatest deformation will be caused by bending. • When M deforms the element of beam, the angle between the cross sections becomes d as shown in Fig. 8. 7(b). 12

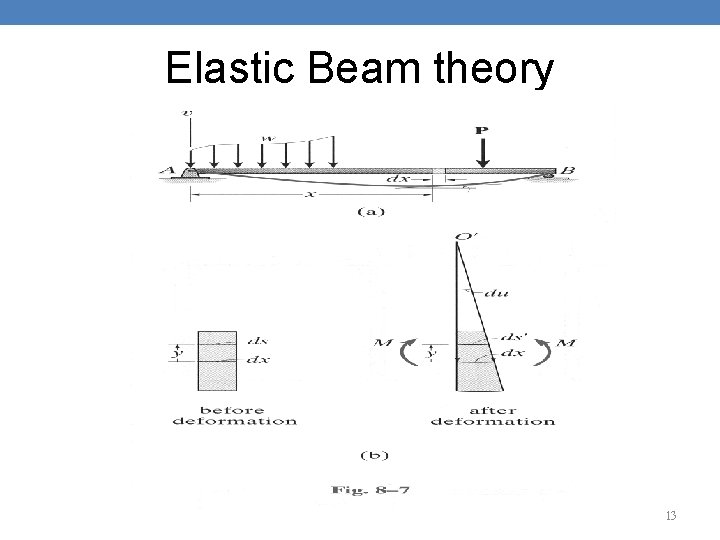
Elastic Beam theory 13

Elastic Beam theory • The arc dx that rep a portion of the elastic curve intersects the neutral axis. • The radius of curvature for this arc is defined as the distance, , which is measured from centroid of curvature O’ to dx. • Any arc on the element other than dx is subjected to normal strain. • The strain in arc ds located at position y from the neutral axis is. 14

Elastic Beam theory • If the material is homogeneous & behaves in a linear manner, then Hooke’s law applies • The flexure formula also applies 15

Elastic Beam theory • Combining these equations, we have: 16

Elastic Beam theory 17

Elastic Beam theory • This equations rep a non-linear second DE. • V=f(x) gives the exact shape of the elastic curve. • The slope of the elastic curve for most structures is very small. • Using small deflection theory, we assume dv/dx ~ 0. • Equation 3 reduces to 18

Elastic Beam theory • By assuming dv/dv ~ 0 ds in Fig. 7(b) is approximately equal to dx • This implies that points on the elastic curve will only be displaced vertically and not horizontally. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 19

The double integration method • M = f(x), successive integration of equation 8. 4 will yield the beam’s slope. – tan = dv/dx = M/EI dx • Equation of elastic curve – V = f(x) = M/EI dx • Consider the beam shown in Fig 8. 8 • The internal moment in regions AB, BC and CD must be written in terms of x 1, x 2 and x 3. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 20

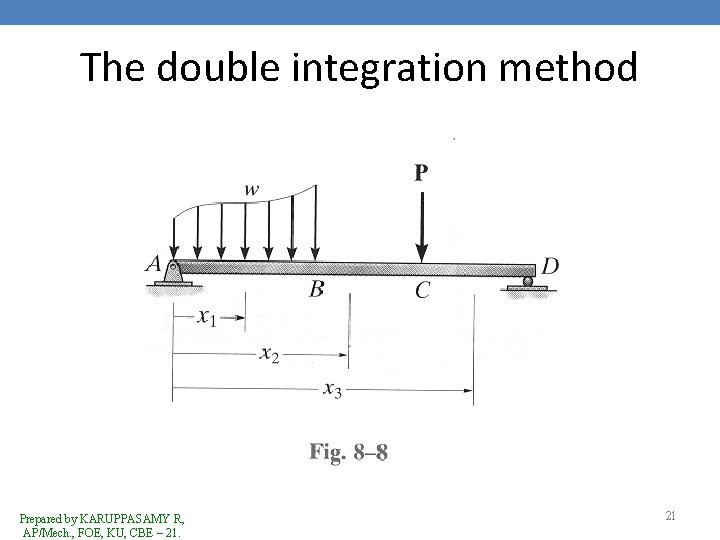
The double integration method Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 21

The double integration method • Once these functions are integrated through the applications of equation 8. 4 & the constants determined, the functions will give the slope & deflection for each region of the beam. • When applying equation 8. 4, it is important to use the proper sign for M as established by the sign convention used in derivation. • +ve v is upward, hence, the +ve slope angle, will be measured counterclockwise from the x-axis. • Reason for this is shown in Fig. 8. 9(b). Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 22

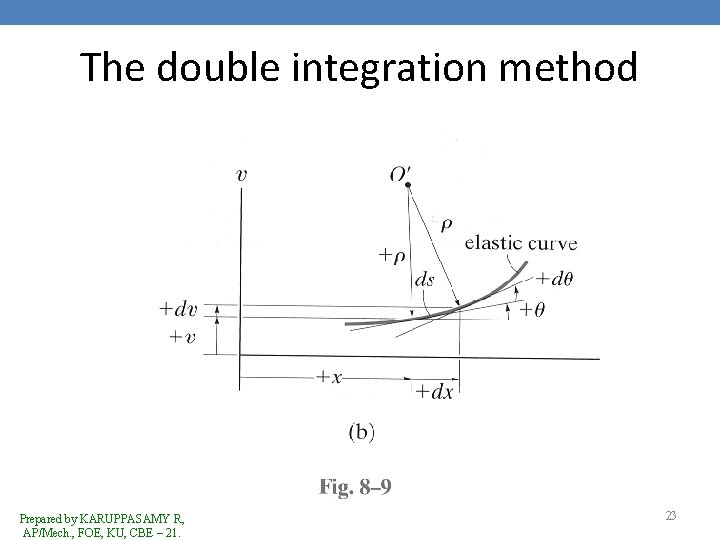
The double integration method Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 23

The double integration method • The constants of integration are determined by evaluating the functions for slope or displacement at a particular point on the beam where the value of the function is known. • These values are called boundary conditions. • Consider the beam shown in Fig 8. 10 • Here x 1 and x 2 coordinates are valid within the regions AB & BC. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 24

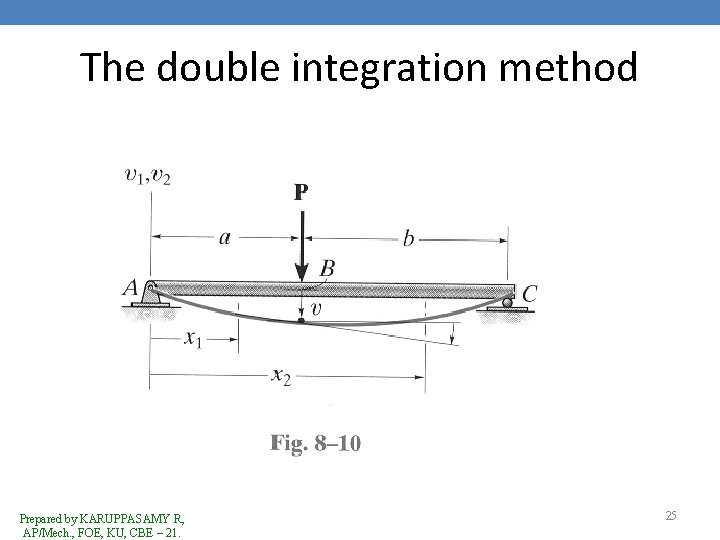
The double integration method Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 25

The double integration method • Once the functions for the slope and deflections are obtained, they must give the same values for slope & deflection at point B. • This is so as for the beam to be physically continuous. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 26

Example 3. 3 • The cantilevered beam shown in Fig. 8. 11(a) is subjected to a couple moment Mo at its end. • Determine the equation of the elastic curve • EI is constant. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 27

Example 3. 3 - solution • The load tends to deflect the beam as shown in Fig. 8. 9(a). • By inspection, the internal moment can be represented throughout the beam using a single x coordinate. • From the free-body diagram, with M acting in +ve direction as shown in Fig. 8. 11(b), we have: Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 28

Example 3. 3 - solution • Applying equation 8. 4 & integrating twice yields: • Using boundary conditions, dv/dx = 0 at x = 0 & v = 0 at x = 0 then C 1 = C 2 =0 Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 29

Example 3. 3 - solution • Substituting these values into earlier equations, we get: • Max slope & displacement occur at A (x = L) for which Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 30

Example 3. 3 - solution • The +ve result for A indicates counterclockwise rotation & the +ve result for v. A indicates that it is upwards. • This agrees with results sketched in Fig. 8. 11(a). • In order to obtain some idea to the actual magnitude of the slope • Consider the beam in Fig. 8. 11(a) to: – Have a length of 3. 6 m – Support a couple moment of 20 k. Nm – Be made of steel having Est = 200 GPa Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 31

Example 3. 3 - solution • If this beam were designed w/o as by assuming the allowable normal stress = yield stress = 250 k. Nm/2 • A W 6 x 9 would be found to be adequate Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 32

Example 3. 3 - solution • Since 2 A = 0. 00280(10 -6)<<1, this justifies the use of equation 8. 4. • Also this numerical application is for cantilevered beam, we have obtained larger values for max and v than would have been obtained if the beam were supported using pins, rollers or other supports. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 33

Example 3. 3 - solution Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 34

Moment-Area theorems • To develop theorems, reference is made to Fig. 8. 13(a). • If we draw the moment diagram for the beam & then divide it by the flexural rigidity, EI, the “M/EI diagram” shown in Fig. 8. 13(b) results. • By equation 8. 2, Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 35

Moment-Area theorems • d on either side of the element dx = the lighter shade area under the M/EI diagram. • Integrating from point A on the elastic curve to point B, Fig 8. 13(c), we have • This equation forms the basis for the first moment-area theorem. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 36

Moment-Area theorems • Theorem 1 – The change in slope between any 2 points on the elastic curve equals the area of the M/EI diagram between the 2 points. • The second moment-area theorem is based on the relative derivation of tangents to the elastic curve. • Shown in Fig 8. 12(c) is a greatly exaggerated view of the vertical deviation dt of the tangents on each side of the differential element, dx. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 37

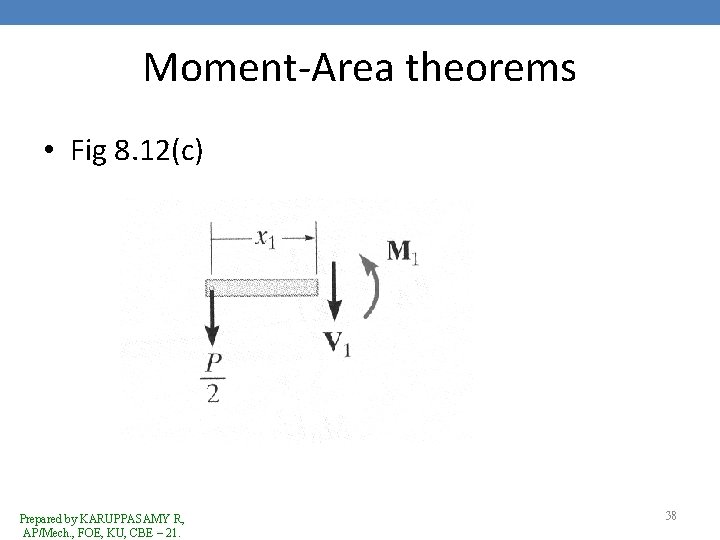
Moment-Area theorems • Fig 8. 12(c) Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 38

Moment-Area theorems • Since slope of elastic curve & its deflection are assumed to be very small, it is satisfactory to approximate the length of each tangent line by x & the arc ds’ by dt. • Using s = r dt = xd • Using equation 8. 2, d = (M/EI) dx • The vertical deviation of the tangent at A with the tangent at B can be found by integration. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 39

Moment-Area theorems • Centroid of an area Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 40

Moment-Area theorems • Theorem 1 – The vertical deviation of the tangent at a point (A) on the elastic curve with the tangent extended from another point (B) equals the “moment” of the area under the M/EI diagram between the 2 points (A & B). – This moment is computed about point A where the derivation is to be determined. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 41

Moment-Area theorems • Provided the moment of a +ve M/EI area from A to B is computed as in Fig. 8. 14(b), it indicates that the tangent at point A is above the tangent to the curve extended from point B as shown in Fig. 8. 14(c). • -ve areas indicate that the tangent at A is below the tangent extended from B. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 42

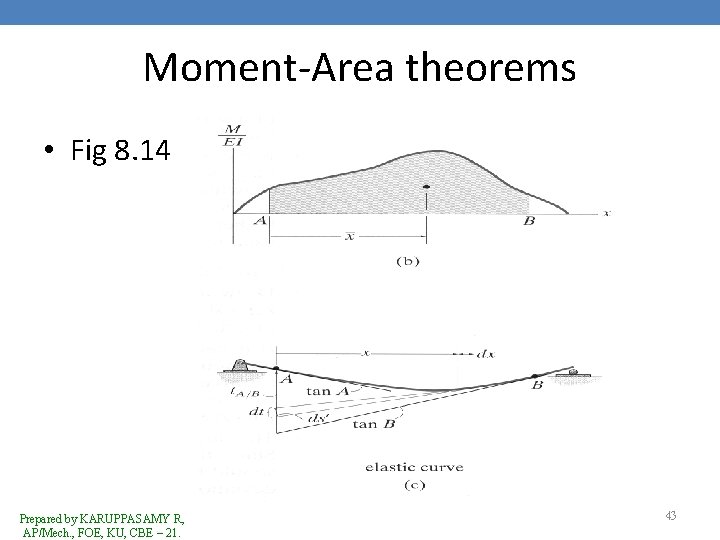
Moment-Area theorems • Fig 8. 14 Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 43

Moment-Area theorems • It is important to realize that the momentarea theorems can only be used to determine the angles and deviations between 2 tangents on the beam’s elastic curve. • In general, they do not give a direct solution for the slope or displacement at a point. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 44

Example 3. 5 • Determine the slope at points B & C of the beam shown in Fig. 8. 15(a). • Take – E = 200 GPa – I = 360(106)mm 4 Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 45

Example 3. 5 - solution • This diagram is shown in Fig. 8. 15(b). • It is easier to solve the problem in terms of EI & substitute the numerical data as a last step. • The 10 k. N load causes the beam to deflect as shown in Fig. 8. 15(c). • Here the tangent at A is always horizontal. • The tangents at B & C are also indicated. • By construction, the angle between tan A and tan B ( B/A) is equivalent to B. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 46

Example 3. 5 - solution • Fig 8. 15 Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 47

Example 3. 5 - solution • Applying Theorem 1, is equal to the area under the M/EI diagram between points A and B. Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 48

Example 3. 5 - solution • Substituting numerical data for E & I • The –ve sign indicates that the angle is measured clockwise from A as shown in Fig. 8. 15(c). • In a similar manner, the area under the M/EI diagram between points A and C equals ( C/A). Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 49

Example 3. 5 - solution Prepared by KARUPPASAMY R, AP/Mech. , FOE, KU, CBE – 21. 50