Unit III Message Authentication message authentication is concerned

























- Slides: 45

Unit III

Message Authentication message authentication is concerned with: protecting the integrity of a message validating identity of originator non-repudiation of origin (dispute resolution) will consider the security requirements then three alternative functions used: hash function message encryption message authentication code (MAC)

Message Security Requirements disclosure traffic analysis masquerade content modification sequence modification timing modification source repudiation destination repudiation

MESSAGE AUTHENTICATION FUNCTION • Message Encryption cipher text generation • Message Authentication code(MAC) function of message and secret key produces fixed length value • Hash Function Any length message to fixed length hash value

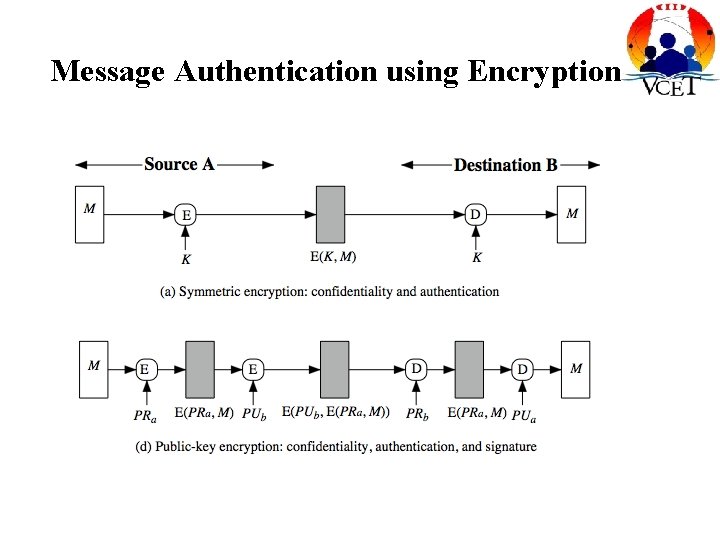
Message Authentication using Encryption

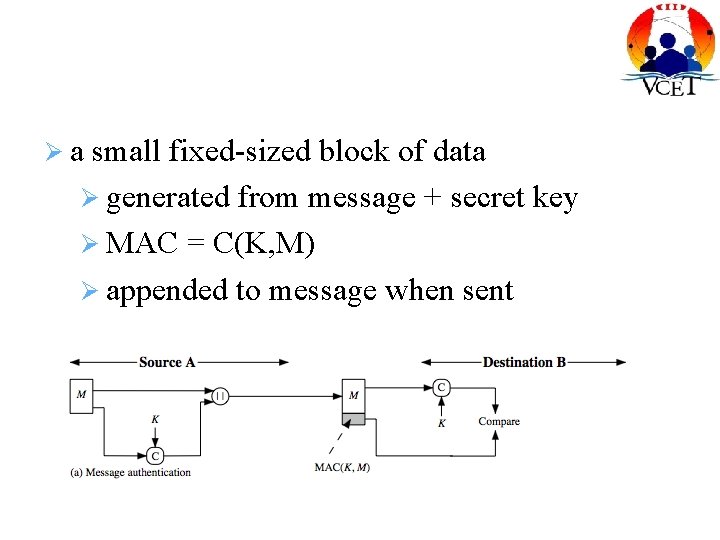
MAC generated by an algorithm that creates a small fixed-sized block depending on both message and secret key like encryption though need not be reversible appended to message as a “signature” receiver performs same computation on message and checks it matches the MAC provides assurance that message is unaltered and comes from sender

a small fixed-sized block of data generated from message + secret key MAC = C(K, M) appended to message when sent

Message Authentication Codes as shown the MAC provides authentication can also use encryption for secrecy generally use separate keys for each can compute MAC either before or after encryption is generally regarded as better done before.

Message Authentication Codes why use a MAC? sometimes only authentication is needed sometimes need authentication to persist longer than the encryption (e. g. archival use) note that a MAC is not a digital signature • Does NOT provide non-repudiation

MAC Properties a MAC is a cryptographic checksum MAC = CK(M) condenses a variable-length message M using a secret key K to a fixed-sized authenticator is a many-to-one function potentially many messages have same MAC but finding these needs to be very difficult

Requirements for MACs taking into account the types of attacks need the MAC to satisfy the following: • • • knowing a message and MAC, is infeasible to find another message with same MACs should be uniformly distributed MAC should depend equally on all bits of the message

Security of MACs like block ciphers have: brute-force attacks exploiting strong collision resistance hash have cost 2 • 128 -bit hash looks vulnerable, 160 -bits better MACs with known message-MAC pairs • can either attack key space (cf. key search) or MAC • at least 128 -bit MAC is needed for security m/ 2

Security of MACs cryptanalytic attacks exploit structure like block ciphers want brute-force attacks to be the best alternative more variety of MACs so harder to generalize about cryptanalysis

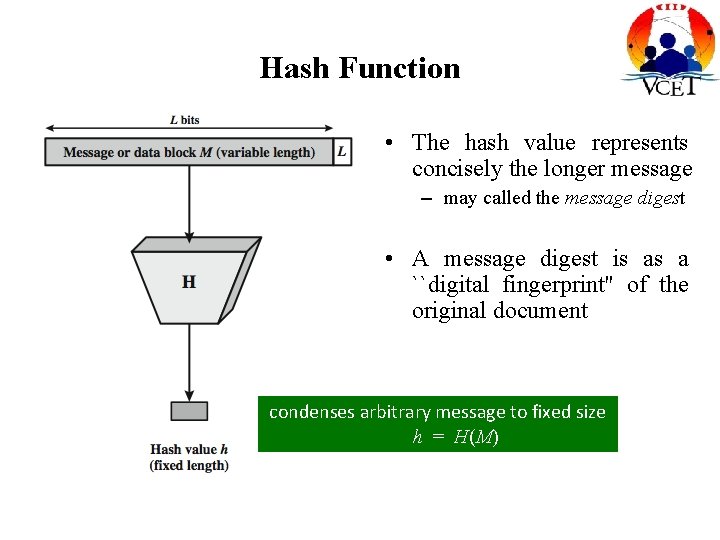
Hash Function • The hash value represents concisely the longer message – may called the message digest • A message digest is as a ``digital fingerprint'' of the original document condenses arbitrary message to fixed size h = H(M)

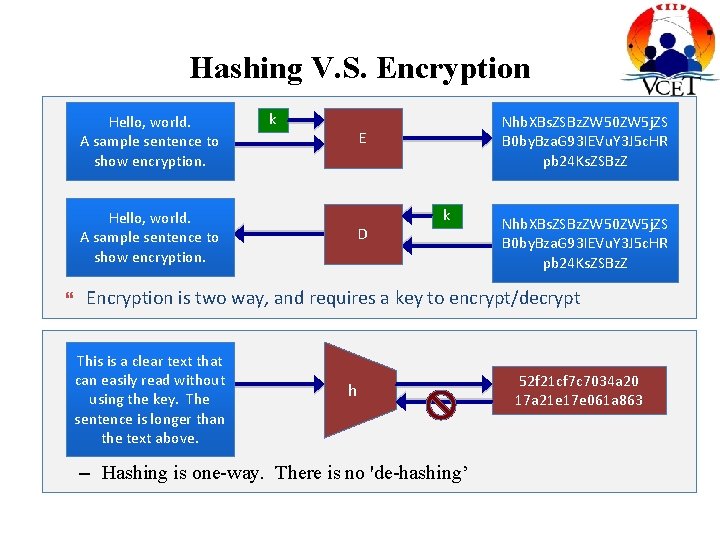
Hashing V. S. Encryption Hello, world. A sample sentence to show encryption. k E Hello, world. A sample sentence to show encryption. Nhb. XBs. ZSBz. ZW 50 ZW 5 j. ZS B 0 by. Bza. G 93 IEVu. Y 3 J 5 c. HR pb 24 Ks. ZSBz. Z D k Nhb. XBs. ZSBz. ZW 50 ZW 5 j. ZS B 0 by. Bza. G 93 IEVu. Y 3 J 5 c. HR pb 24 Ks. ZSBz. Z Encryption is two way, and requires a key to encrypt/decrypt This is a clear text that can easily read without using the key. The sentence is longer than the text above. h – Hashing is one-way. There is no 'de-hashing’ 52 f 21 cf 7 c 7034 a 20 17 a 21 e 17 e 061 a 863

HASH FUNCTIONS a)Encrypt message and Hash code b)Encrypt hash code-secret key c)Encrypt hash code-public key encryption d)Encrypt result of step C by secret key e)Compute hash code value for that message by combining both message and secret value f)Encrypt the result of e

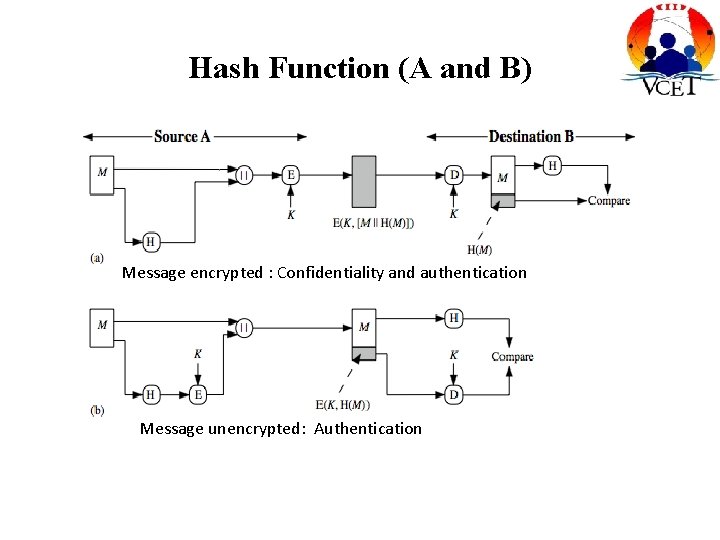
Hash Function (A and B) Message encrypted : Confidentiality and authentication Message unencrypted: Authentication

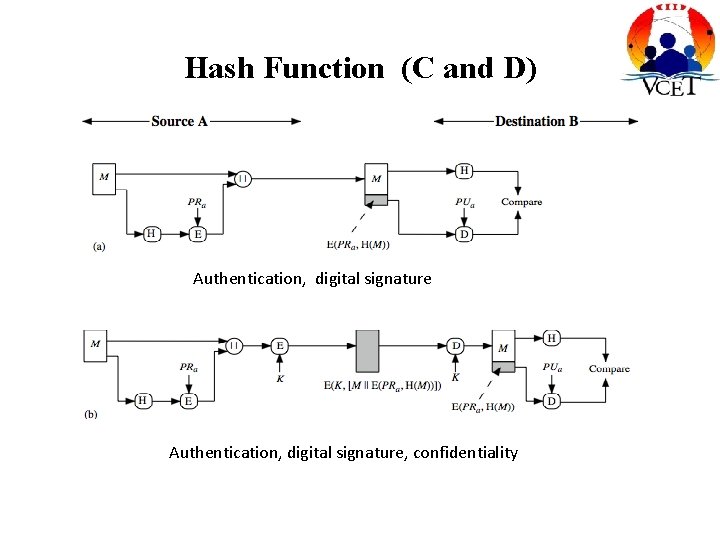
Hash Function (C and D) Authentication, digital signature, confidentiality

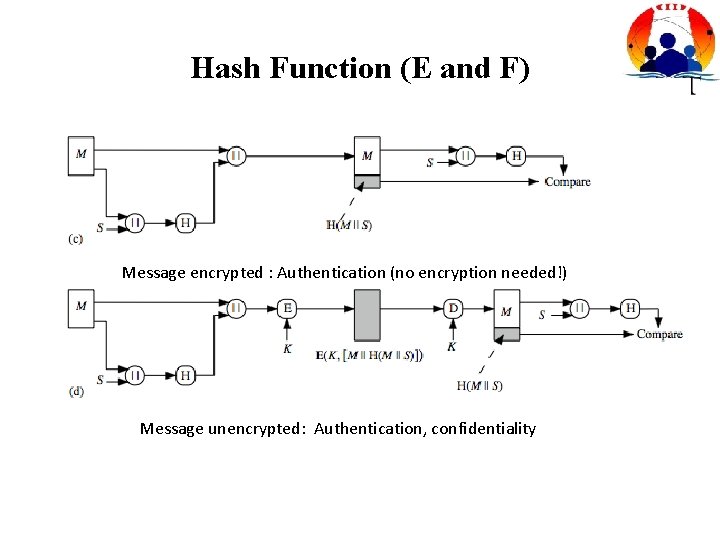
Hash Function (E and F) Message encrypted : Authentication (no encryption needed!) Message unencrypted: Authentication, confidentiality

Hash Function Properties • Arbitrary-length message to fixed-length digest • Preimage resistant (One-way property) • Second preimage resistant (Weak collision resistant) • Collision resistant (Strong collision resistance)

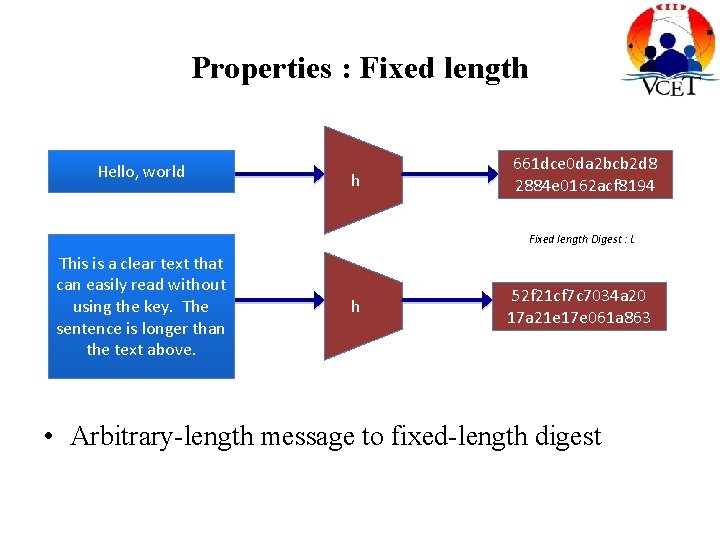
Properties : Fixed length Hello, world h 661 dce 0 da 2 bcb 2 d 8 2884 e 0162 acf 8194 Fixed length Digest : L This is a clear text that can easily read without using the key. The sentence is longer than the text above. h 52 f 21 cf 7 c 7034 a 20 17 a 21 e 17 e 061 a 863 • Arbitrary-length message to fixed-length digest

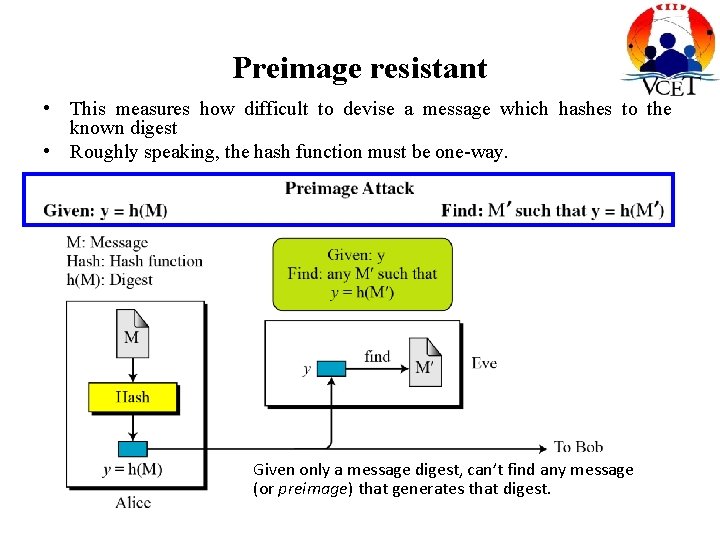
Preimage resistant • This measures how difficult to devise a message which hashes to the known digest • Roughly speaking, the hash function must be one-way. Given only a message digest, can’t find any message (or preimage) that generates that digest.

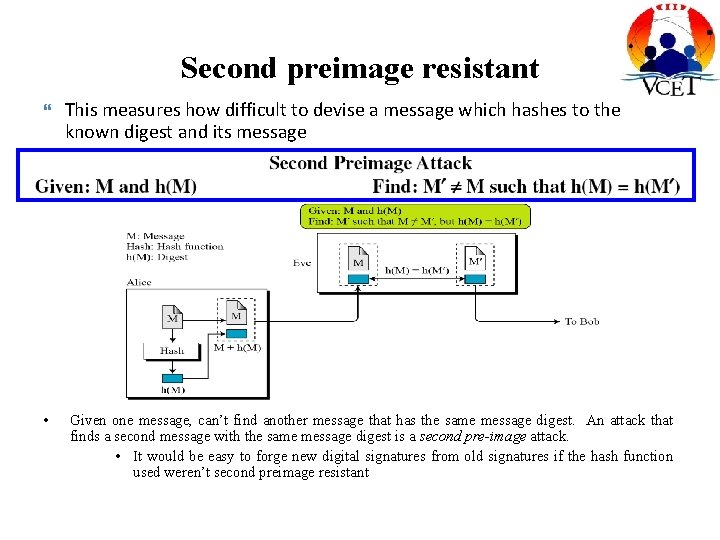
Second preimage resistant • This measures how difficult to devise a message which hashes to the known digest and its message Given one message, can’t find another message that has the same message digest. An attack that finds a second message with the same message digest is a second pre-image attack. • It would be easy to forge new digital signatures from old signatures if the hash function used weren’t second preimage resistant

Collision Resistant – Can’t find any two different messages with the same message digest • Collision resistance implies second preimage resistance • Collisions, if we could find them, would give signatories a way to repudiate their signatures

Hash Functions Family • MD (Message Digest) – Designed by Ron Rivest – Family: MD 2, MD 4, MD 5 • SHA (Secure Hash Algorithm) – Designed by NIST – Family: SHA-0, SHA-1, and SHA-2 • SHA-2: SHA-224, SHA-256, SHA-384, SHA-512 • SHA-3: New standard in competition • RIPEMD (Race Integrity Primitive Evaluation Message Digest) – Developed by Katholieke University Leuven Team – Family : RIPEMD-128, RIPEMD-160, RIPEMD-256, RIPEMD-320,

MD 5, SHA-1, and RIPEMD-160

MD 2, MD 4 and MD 5 • Family of one-way hash functions by Ronald Rivest – All produces 128 bits hash value • MD 2: 1989 – Optimized for 8 bit computer – Collision found in 1995 • MD 4: 1990 – Full round collision attack found in 1995 • MD 5: 1992 – – Specified as Internet standard in RFC 1321 since 1997 it was theoretically not so hard to create a collision Practical Collision MD 5 has been broken since 2004 CA attack published in 2007

Secure Hash Algorithm SHA originally designed by NIST & NSA in 1993 was revised in 1995 as SHA-1 US standard for use with DSA signature scheme standard is FIPS 180 -1 1995, also Internet RFC 3174 based on design of MD 4 with key differences produces 160 -bit hash values recent 2005 results on security of SHA-1 have raised concerns on its use in future applications

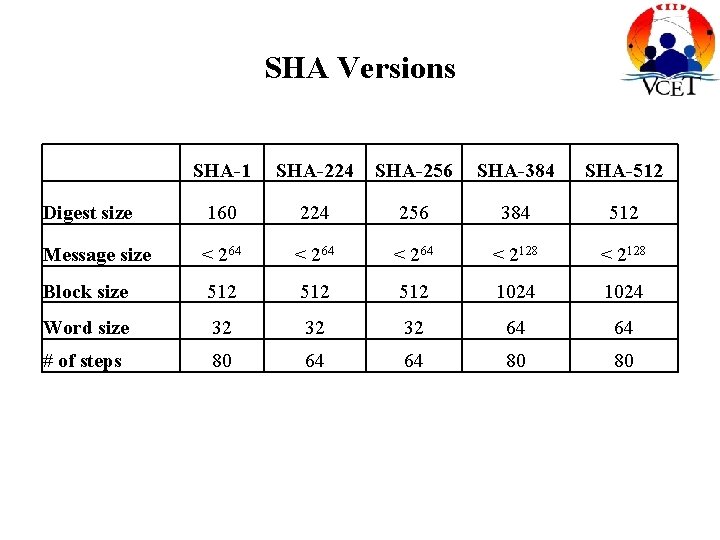
SHA Versions SHA-1 SHA-224 SHA-256 SHA-384 SHA-512 Digest size 160 224 256 384 512 Message size < 264 < 2128 Block size 512 512 1024 Word size 32 32 32 64 64 # of steps 80 64 64 80 80

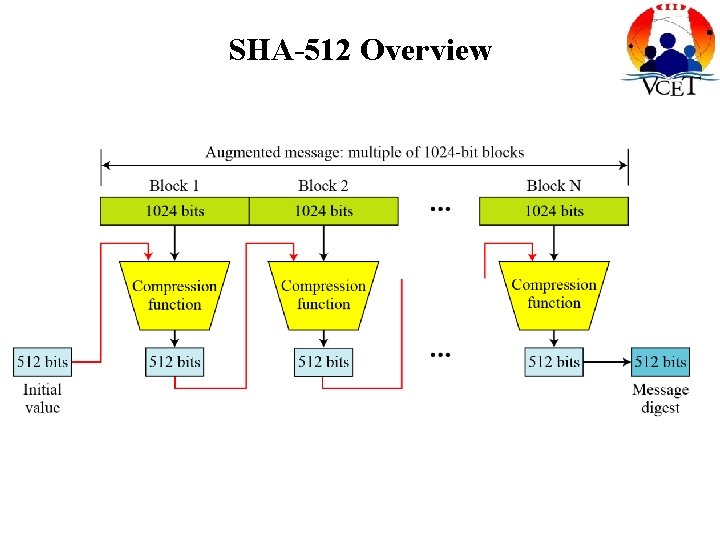
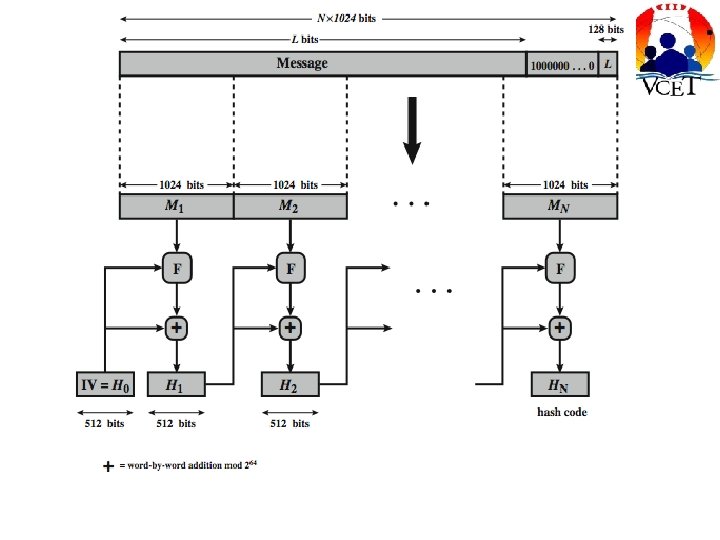
SHA-512 Overview

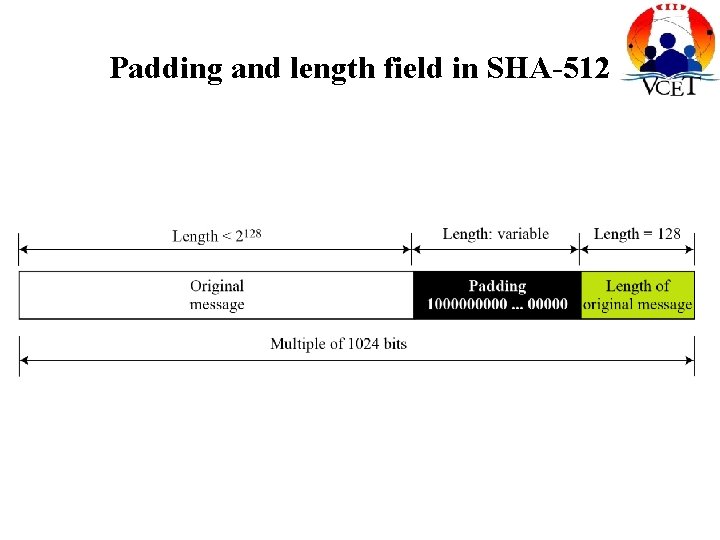
STEPS • Append Padding bits • Append padding bit length • Message is considered as a ‘L’ no. of blocks each contains 512 bits • ‘L’ no. of Message digest Hash functions are used as an iterations

Padding and length field in SHA-512



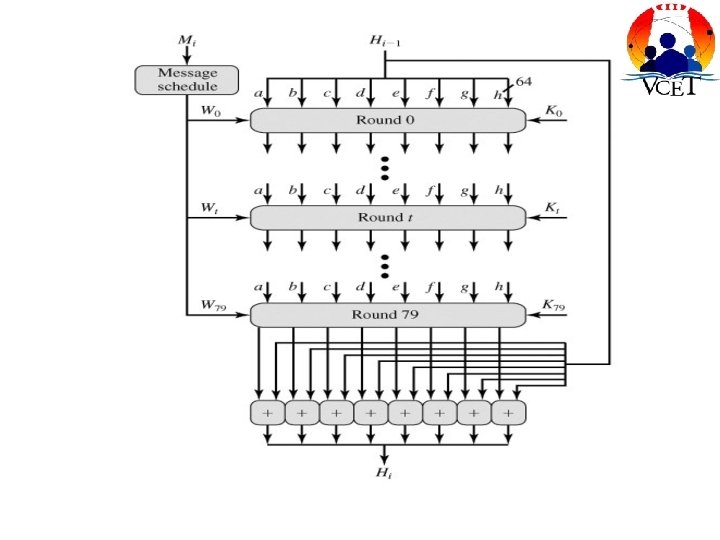
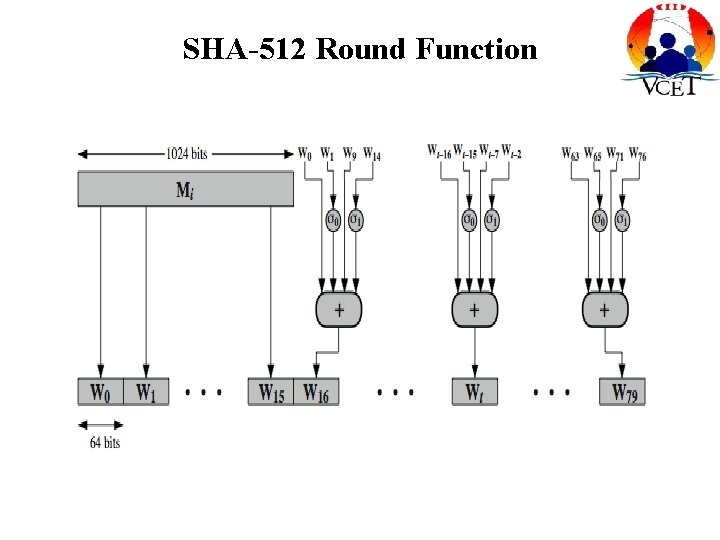
SHA-512 Round Function

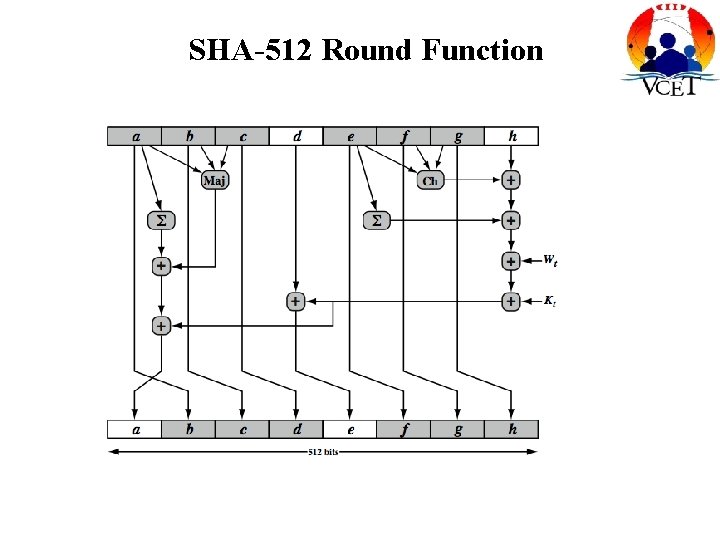
SHA-512 Round Function

Function Elements • • • Ch(e, f, g) = (e AND f) XOR (NOT e AND g) Maj(a, b, c) = (a AND b) XOR (a AND c) XOR (b AND c) ∑(a) = ROTR(a, 28) XOR ROTR(a, 34) XOR ROTR(a, 39) ∑(e) = ROTR(e, 14) XOR ROTR(e, 18) XOR ROTR(e, 41) + = addition modulo 2^64 – Kt = a 64 -bit additive constant – Wt = a 64 -bit word derived from the current 512 -bit input block. – ROTR(x, n) Circular right shift of the 64 bit argument x by n bits

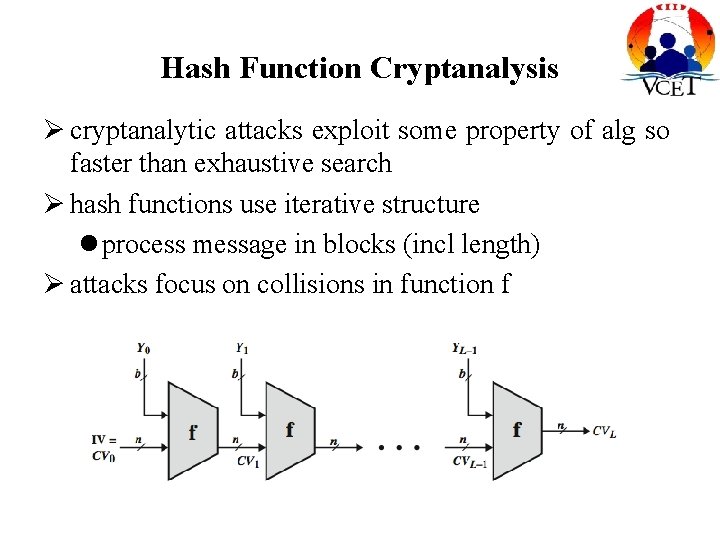
Hash Function Cryptanalysis cryptanalytic attacks exploit some property of alg so faster than exhaustive search hash functions use iterative structure process message in blocks (incl length) attacks focus on collisions in function f

Attacks on Hash Functions have brute-force attacks and cryptanalysis a preimage or second preimage attack find y s. t. H(y) equals a given hash value collision resistance find two messages x & y with same hash so H(x) = H(y)

Birthday Attack • How many people do you need so that the probability of having two of them share the same birthday is > 50% ? • N distinct values, k randomly chosen ones – P(N, i) = prob(i randomly selected values from 1. . N have at least one match) – P(N, 2) = 1/N – P(N, i+1) = P(N, i)+(1 -P(N, i))(i/N) • For P(N, k)>0. 5, need k ≈ N 1/2 For m bits hash code, hence value 2 m/2 determines strength of hash code against brute-force attacks 128 -bits inadequate, 160 -bits suspect

MD 5

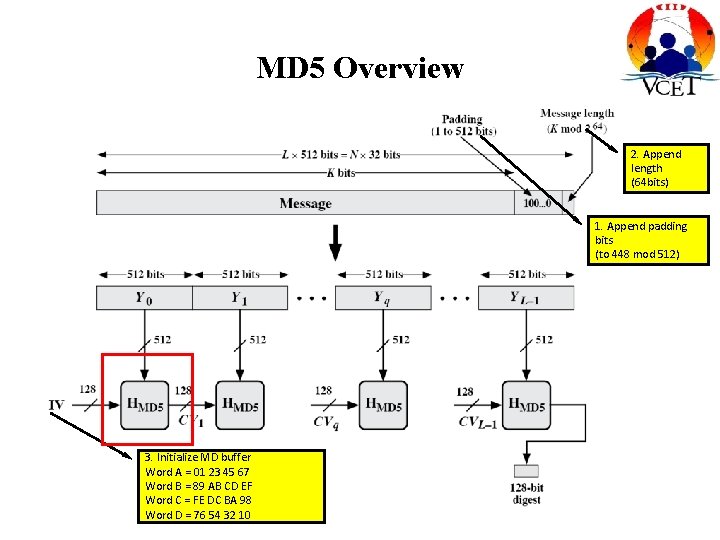
MD 5 Overview 2. Append length (64 bits) 1. Append padding bits (to 448 mod 512) 3. Initialize MD buffer Word A = 01 23 45 67 Word B = 89 AB CD EF Word C = FE DC BA 98 Word D = 76 54 32 10

STEPS • Append Padding bits • Append padding bit length • Message is considered as a ‘L’ no. of blocks each contains 512 bits • ‘L’ no. of Message digest Hash functions are used as an iterations

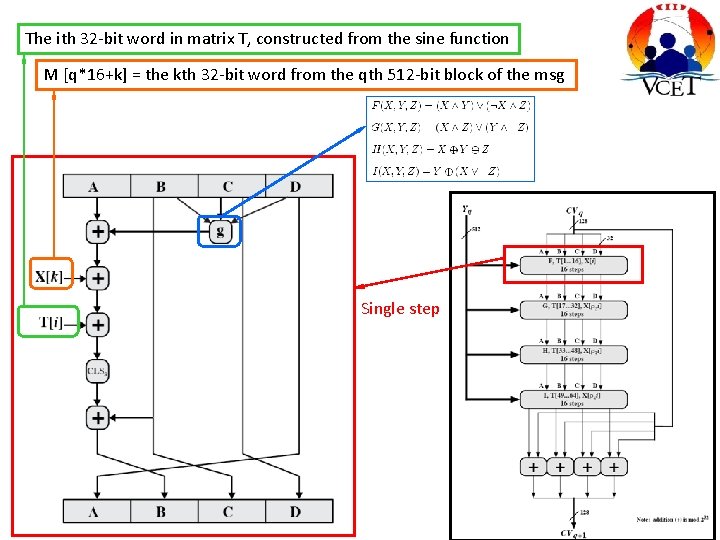
The ith 32 -bit word in matrix T, constructed from the sine function M [q*16+k] = the kth 32 -bit word from the qth 512 -bit block of the msg Single step

continues 1. Each MD 5 contains 64 steps that can be divided into 4 rounds. Each rounds contains 16 steps 2. Each round contains three inputs 512 bit message 128 bit buffer message t[i]=constructed from sine function [2^32 *abs(sin (i))] x[i]=no change X[k] = M [q*16+k] P 2[i]=(1+5 i)mod 16 P 3[i]=(5+3 i)mod 16 P 3[i]=7 i mod 16