UNIT III DYNAMIC PROGRAMMING ALGORITHMS Developing a Dynamic

UNIT III DYNAMIC PROGRAMMING ALGORITHMS Developing a Dynamic Programming Algorithm-Subtle Points- Question for the Little Bird- Sub instances and Sub solutions-Set of Substances-Decreasing Time and Space-Number of Solutions-Code. Reductions and NPCompleteness-Satisfiability-Proving NP-Completeness- 3 -Coloring- Bipartite Matching. Randomized Algorithms-Randomness to Hide Worst Cases. Optimization Problems with a Random Structure.

Dynamic Programming • A hard topic. • I try to provide a unified way to think of it and a fixed set of steps to follow. • Even if you don’t get the details of the algorithm correct, at least get the right structure. • I provide analogies (little bird) to make it hopefully more fun & easier to follow.

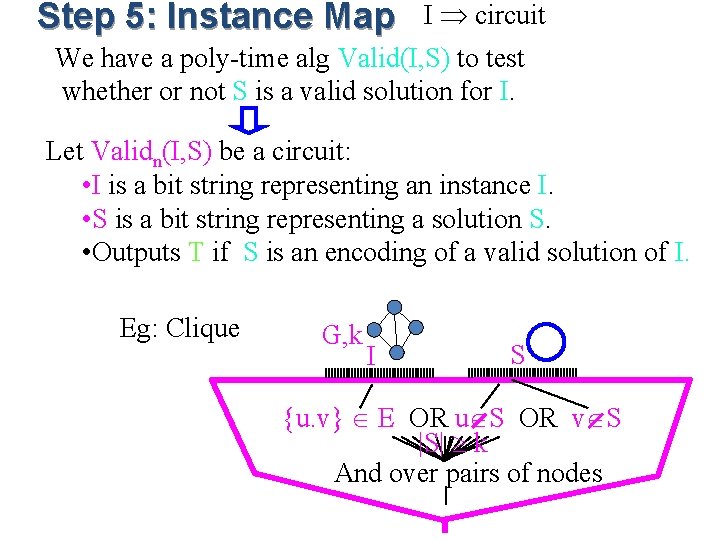
Non-Deterministic Poly-Time Decision Problems (NP) • An optimization problem • Each solution is either valid or not (no cost) • The output is • Yes, it has a valid solution. • No, it does not • the solution is not returned • Eg: Given graph and integer <G, k>, does G have a clique of size k?

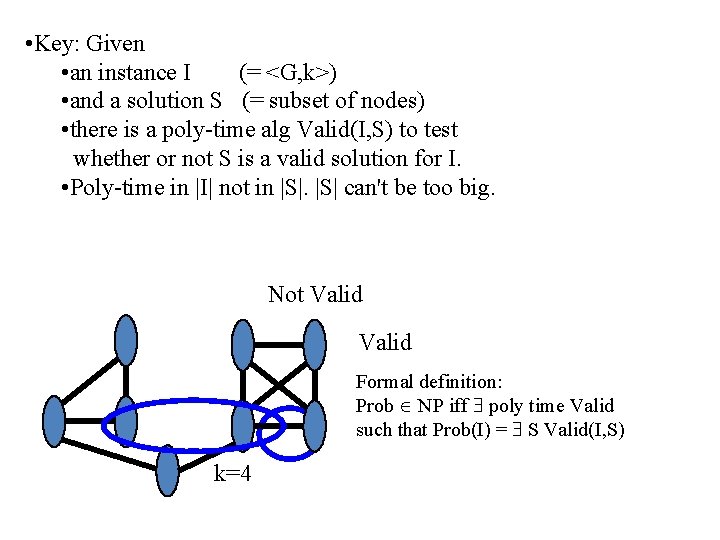
• Key: Given • an instance I (= <G, k>) • and a solution S (= subset of nodes) • there is a poly-time alg Valid(I, S) to test whether or not S is a valid solution for I. • Poly-time in |I| not in |S| can't be too big. Not Valid Formal definition: Prob NP iff poly time Valid such that Prob(I) = S Valid(I, S) k=4

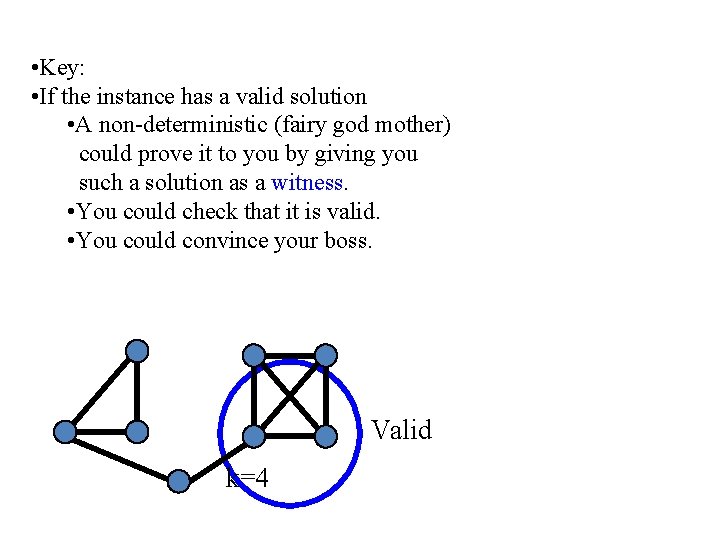
• Key: • If the instance has a valid solution • A non-deterministic (fairy god mother) could prove it to you by giving you such a solution as a witness. • You could check that it is valid. • You could convince your boss. Valid k=4

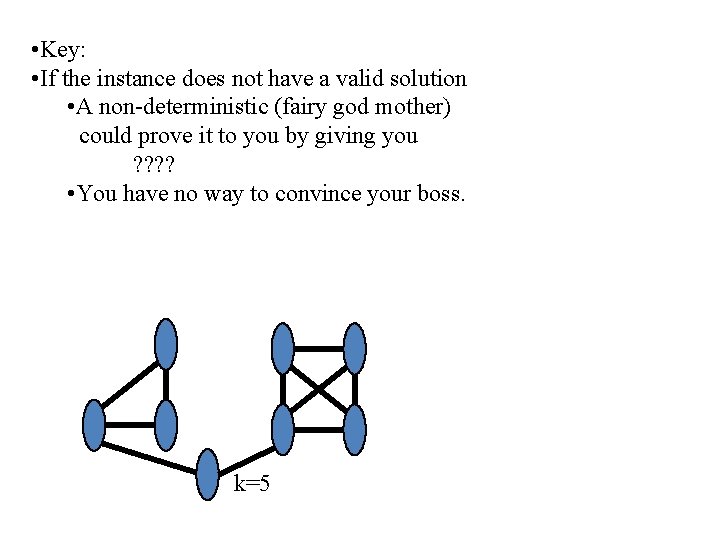
• Key: • If the instance does not have a valid solution • A non-deterministic (fairy god mother) could prove it to you by giving you ? ? • You have no way to convince your boss. k=5

Non-Deterministic Poly-Time (NP) • Example: 3 -Col: • Instance: A graph G. • Solution: Colouring C nodes of G with 3 colours such that every edge has two colours. • G is a Yes instance if there is such a colouring. • Given an instance G and a solution C, there is a poly-time alg Valid(G, C) to test whether or not C is a valid 3 colouring of G. 3 -Col NP.

Non-Deterministic Poly-Time (NP) • Example: Airplane Wing: • Instance: Requirements I of the wing. • Solution: A description S of how to make the wing. • I is a Yes instance if there is such a wing. • Given an instance I and a proof S, there is a poly-time alg Valid(I, S) to test whether or not S is a valid solution for I. Airplane Wing NP. I = [weight, lift, cost, …]

Reductions Palg ≤poly Poracle • Reduction: Design a fast algorithm for one computational problem, using a supposedly fast algorithm for another problem as a subroutine.

NP vs Co-NP Preserving Reductions • Definition is asymmetric. • There is a witness that a graph has a 3 -Col. • There is no known witness that a graph has no 3 -Col. Cook Reduction: • Design any fast algorithm for Palg using a supposed fast algorithm for Poracle as a subroutine. Karp Reduction: The algorithm for Palg calls that for Poracle only once Yes & No

Karp Reduction: Yes & No We will only consider reductions of this simple form. Because they preserve NP vs Co-NP

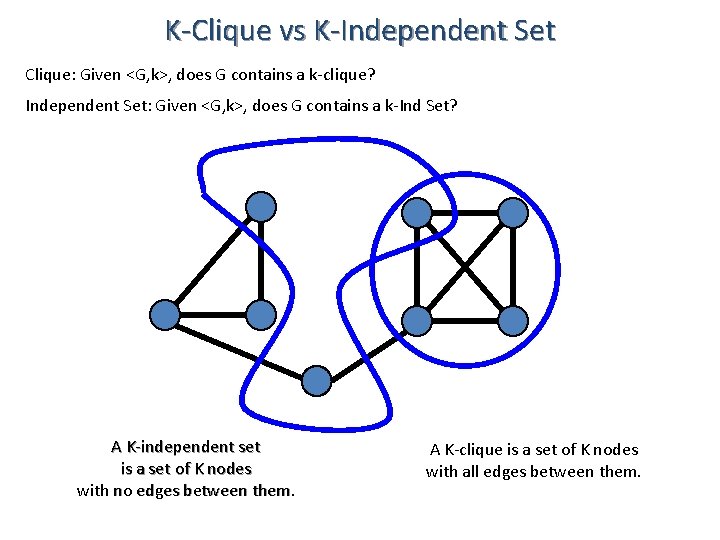
• Problem Pnew is NP-Complete • Pnew not too hard. • Pnew NP

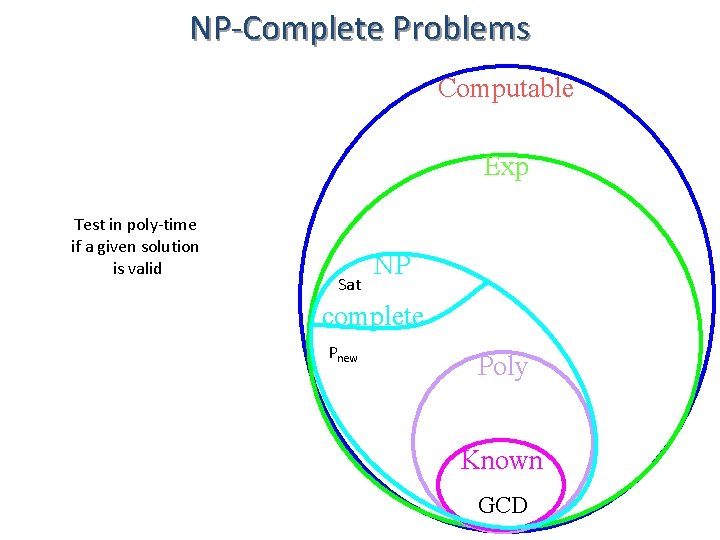
NP-Complete Problems Computable Exp Test in poly-time if a given solution is valid Sat NP complete Pnew Poly Known GCD

NP-Complete Problems Computable Problem Pnew is NP-Complete • Pnew not too hard. Exp • Pnew NP • Pnew sufficiently hard. • P NP, P ≤poly Pnew NP Sat • Easier: Sat ≤poly Pnew • Cook: P ≤poly Sat complete Pnew Poly Known GCD

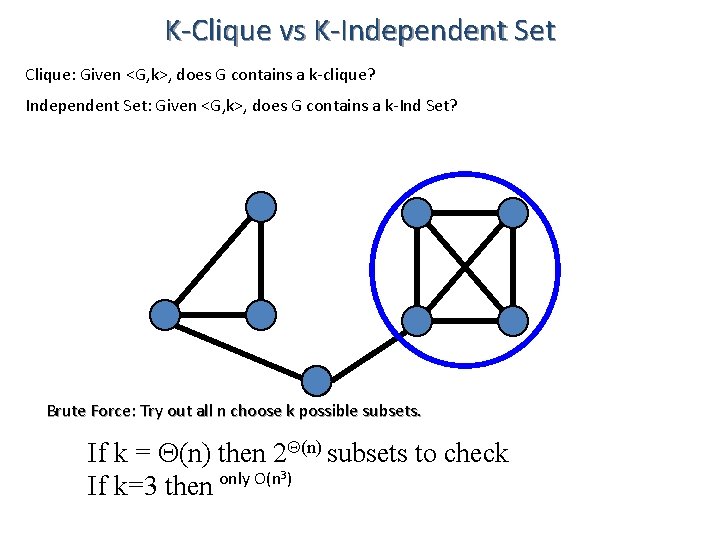
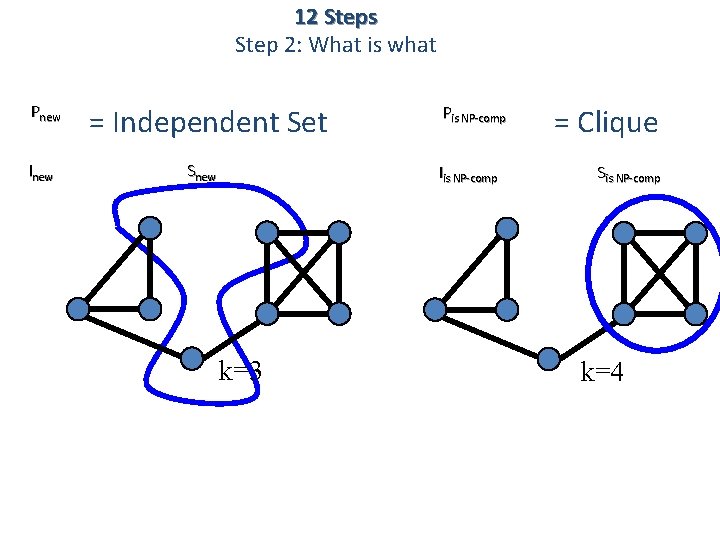
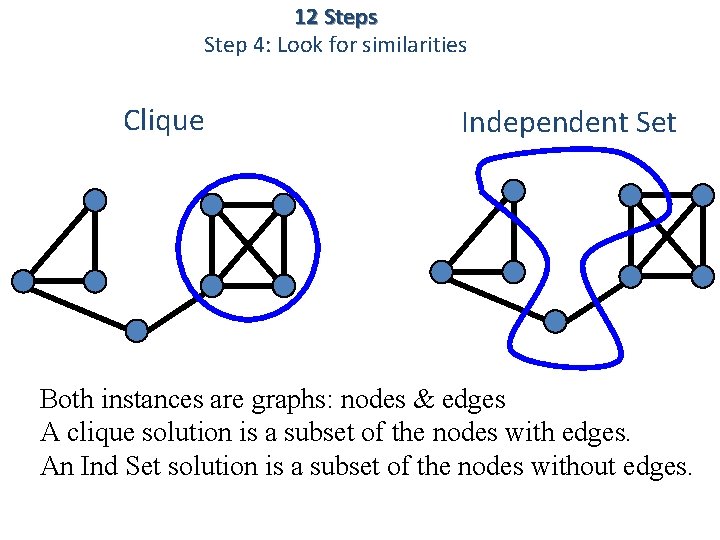
K-Clique vs K-Independent Set Clique: Given <G, k>, does G contains a k-clique? Independent Set: Given <G, k>, does G contains a k-Ind Set? A K-independent set is a set of K nodes with no edges between them. A K-clique is a set of K nodes with all edges between them.

K-Clique vs K-Independent Set Clique: Given <G, k>, does G contains a k-clique? Independent Set: Given <G, k>, does G contains a k-Ind Set? Brute Force: Try out all n choose k possible subsets. If k = (n) then 2 (n) subsets to check only O(n 3) If k=3 then

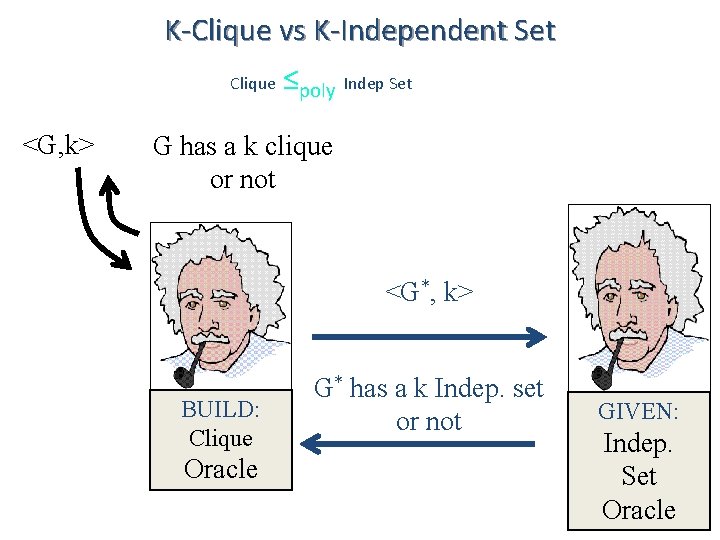
K-Clique vs K-Independent Set Clique <G, k> ≤poly Indep Set G has a k clique or not <G*, k> BUILD: Clique Oracle G* has a k Indep. set or not GIVEN: Indep. Set Oracle

K-Clique vs K-Independent Set Clique <G, k> ≤poly Indep Set G has a k clique or not <G*, k> Proof of correctness: G* has a k Indep. set BUILD: Our oracle says yes to <G, k> or not Clique iff Old oracle says yes to <G*, k> iff G* has Oracle a k indep. set iff G has a k clique GIVEN: Indep. Set Oracle

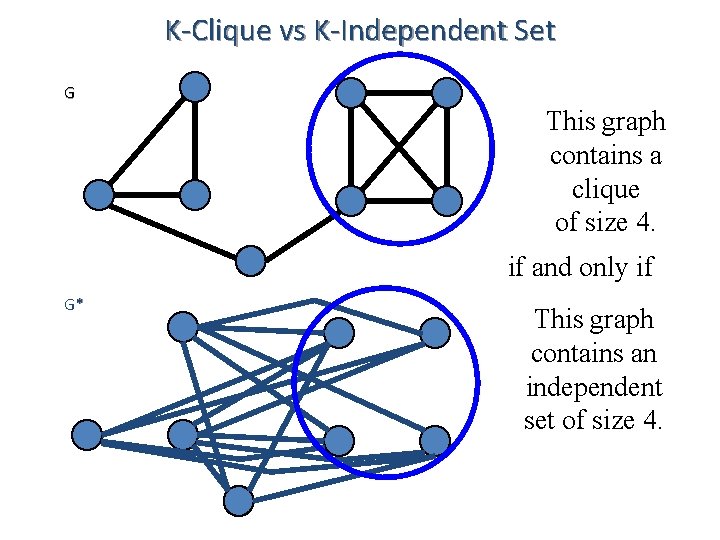
K-Clique vs K-Independent Set G G* G* has edge if and only if G does not

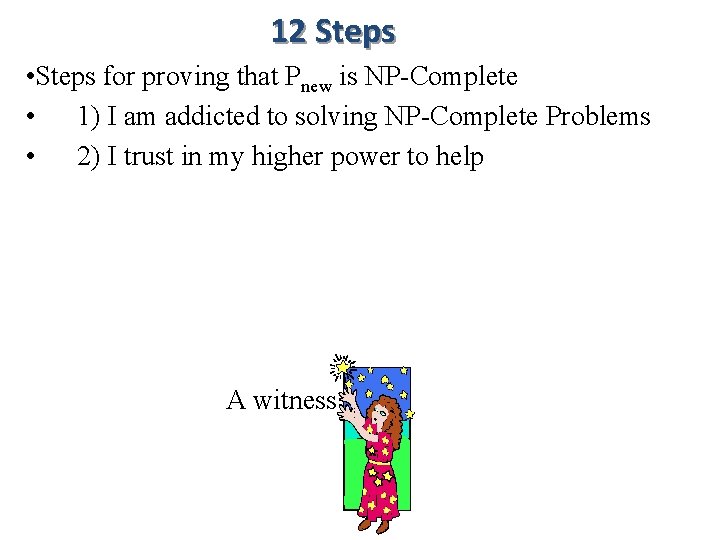
K-Clique vs K-Independent Set G This graph contains a clique of size 4. if and only if G* This graph contains an independent set of size 4.

12 Steps • Steps for proving that Pnew is NP-Complete • 1) I am addicted to solving NP-Complete Problems • 2) I trust in my higher power to help A witness

12 Steps • Steps for proving that Pnew is NP-Complete • 0) Pnew NP • 1) What to reduce it to 2) What is what 3) Direction of reduction & Code 4) Look for similarities 5) Instance Map 6) Solution Map 7) Valid to Valid 8) Reverse Solution Map 9) Valid to Valid 10) Working Algorithm 11) Running Time

12 Steps Step 0: Pnew NP Formal definition: Pnew NP iff poly time Valid such that Pnew(I) = S Valid(I, S) • Design poly-time algorithm Valid(I, S) • which determines whether a given solution S • is valid for a given instance I.

12 Steps Step 1: What to reduce it to Palg ≤poly Poracle Choose a problem Pis NP-comp that is as similar to Pnew as possible and that is already known to be NP-Complete.

12 Steps Step 2: What is what Pnew Inew = Independent Set Snew Pis NP-comp Iis NP-comp k=3 = Clique Sis NP-comp k=4

12 Steps Step 3: Direction of reduction & Code Reduce Pnew to Pis NP-comp or Pis NP-comp to Pnew? Pis NP-comp ≤poly Pnew Palg ≤poly Poracle

12 Steps Step 3: Direction of reduction & Code

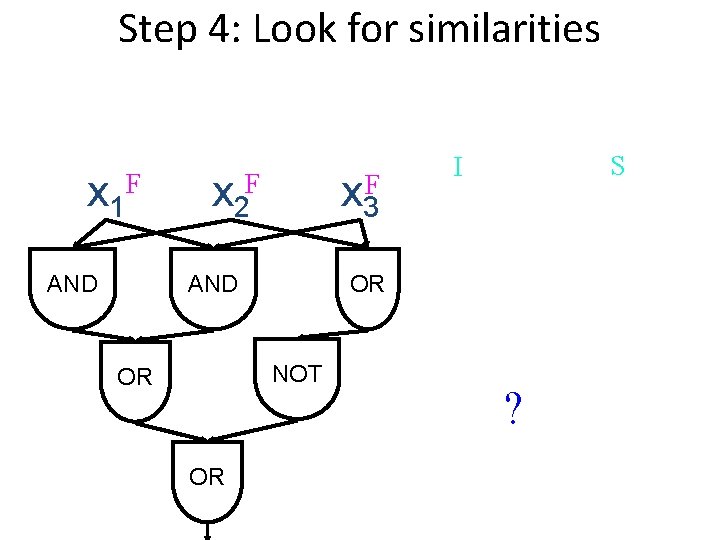
12 Steps Step 4: Look for similarities Clique Independent Set Both instances are graphs: nodes & edges A clique solution is a subset of the nodes with edges. An Ind Set solution is a subset of the nodes without edges.

12 Steps Step 5: Instance Map

12 Steps Step 5: Instance Map Ialg Ioracle = Instance. Map(Ialg)

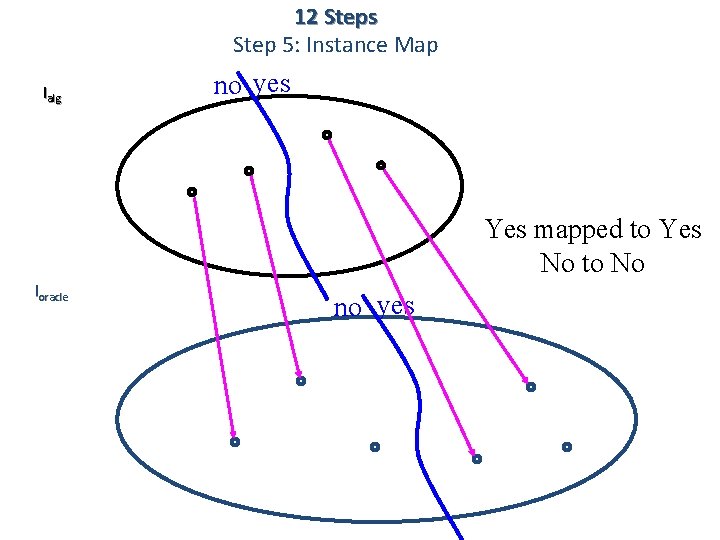
12 Steps Step 5: Instance Map Ialg no yes Yes mapped to Yes No to No Ioracle no yes

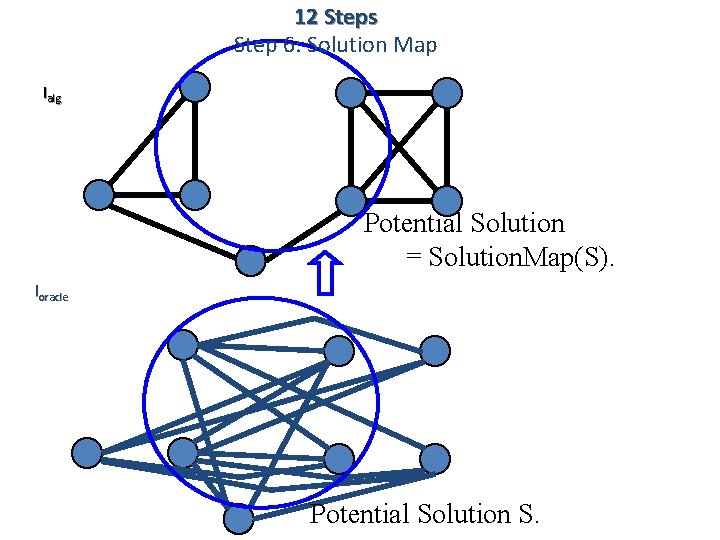
12 Steps Step 6: Solution Map

12 Steps Step 6: Solution Map Ialg Potential Solution = Solution. Map(S). Ioracle Potential Solution S.

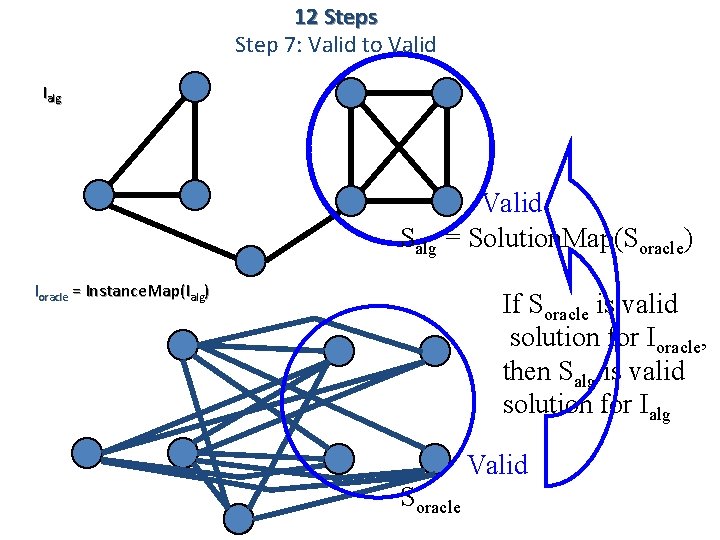
12 Steps Step 7: Valid to Valid Ialg Valid Salg = Solution. Map(Soracle) Ioracle = Instance. Map(Ialg) If Soracle is valid solution for Ioracle, then Salg is valid solution for Ialg Valid Soracle

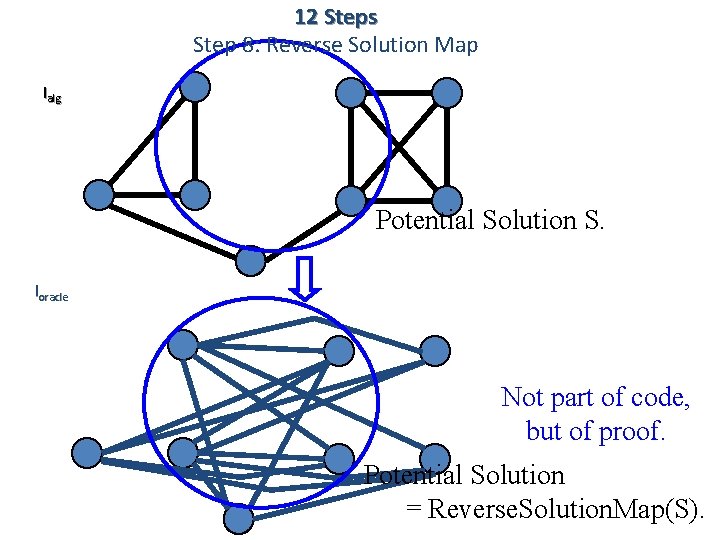
12 Steps Step 8: Reverse Solution Map Ialg Potential Solution S. Ioracle Not part of code, but of proof. Potential Solution = Reverse. Solution. Map(S).

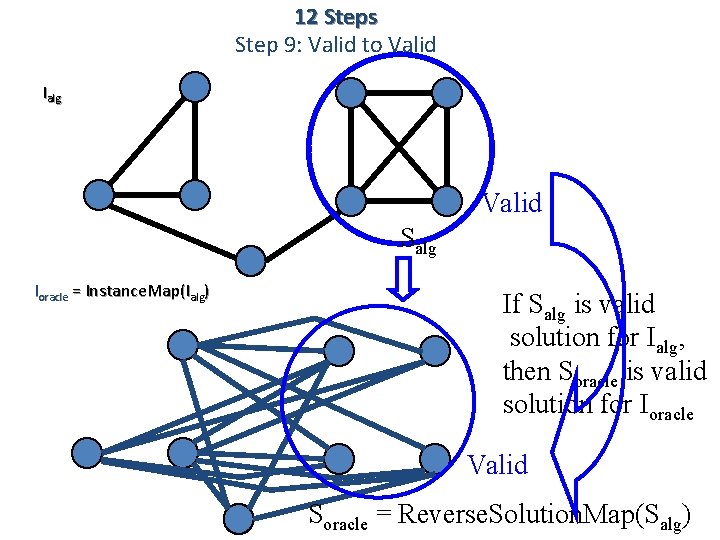
12 Steps Step 9: Valid to Valid Ialg Valid Salg Ioracle = Instance. Map(Ialg) If Salg is valid solution for Ialg, then Soracle is valid solution for Ioracle Valid Soracle = Reverse. Solution. Map(Salg)

12 Steps Step 10: Working Algorithm Our Algalg says yes to Ialg iff old Algoracle says yes to Ioracle iff Ioracle has a valid solution Soracle iff Ialg has a valid solution Salg iff Ialg is a yes instance. 6&7 Steps 8&9

12 Steps Step 11: Running Time Algalg(Ialg) is poly time if the following are poly time: Algoracle(Ioracle) Assumed Ioracle = Instance. Map(Ialg) Salg = Solution. Map(Soracle) Your job

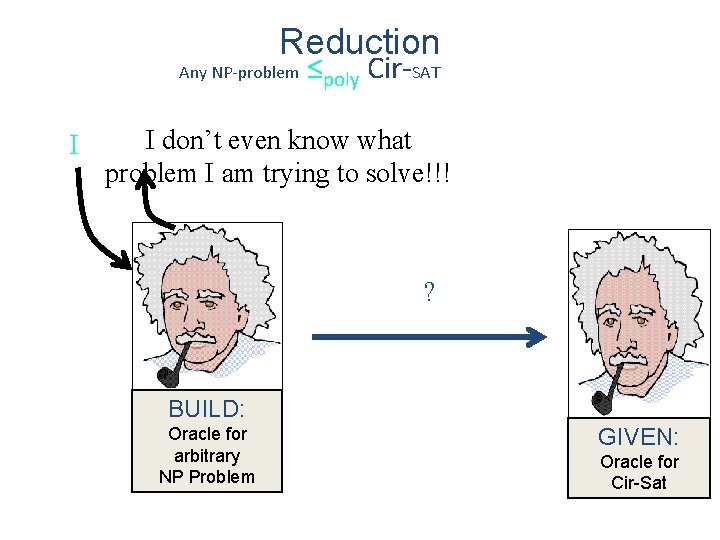
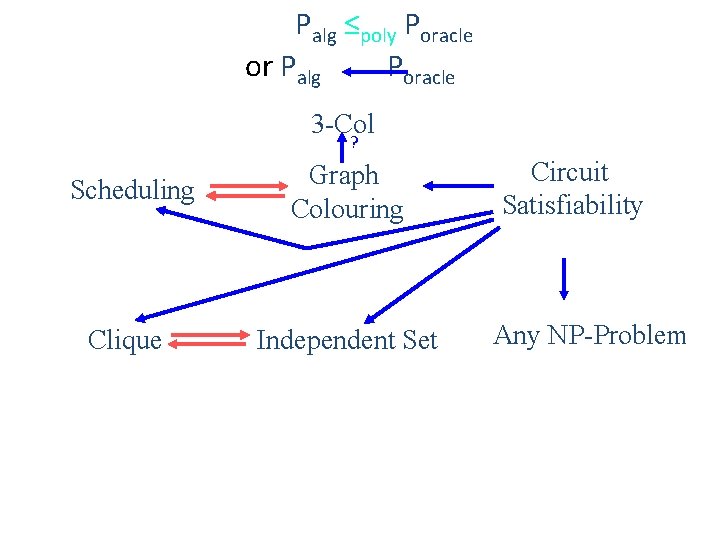
Palg ≤poly Poracle or Palg Poracle Scheduling Graph Colouring Clique Independent Set Circuit Satisfiability Any NP-Problem This will prove that Cir-SAT is NP-Complete.

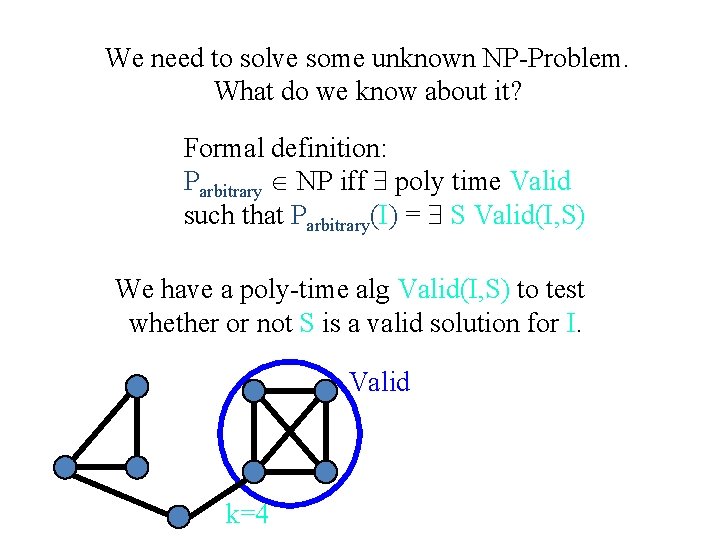
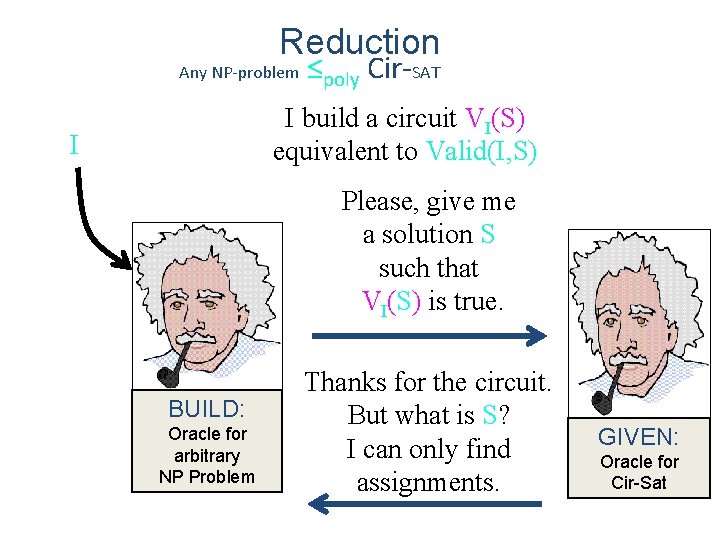
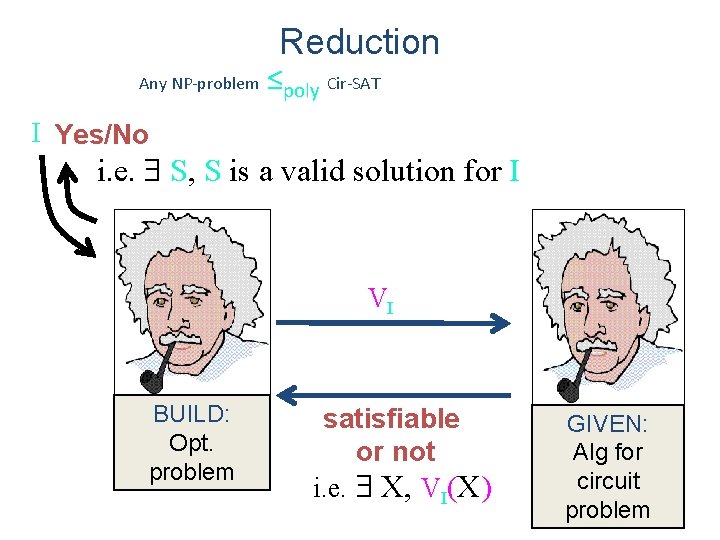
Reduction Any NP-problem I ≤poly Cir-SAT I don’t even know what problem I am trying to solve!!! ? BUILD: Oracle for arbitrary NP Problem GIVEN: Oracle for Cir-Sat

We need to solve some unknown NP-Problem. What do we know about it? Formal definition: Parbitrary NP iff poly time Valid such that Parbitrary(I) = S Valid(I, S) We have a poly-time alg Valid(I, S) to test whether or not S is a valid solution for I. Valid k=4

Reduction Any NP-problem ≤poly Cir-SAT I Please, give me a solution S such that Valid(I, S) is true. BUILD: Oracle for arbitrary NP Problem That looks like a Turing Machine. I only know about circuits GIVEN: Oracle for Cir-Sat

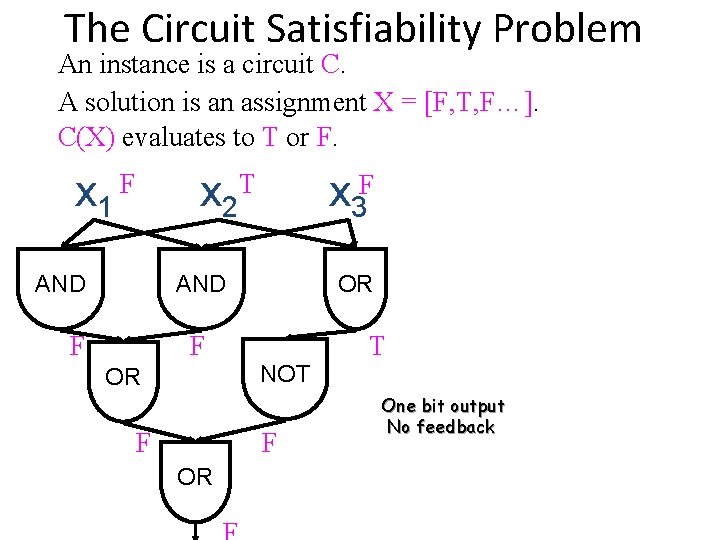
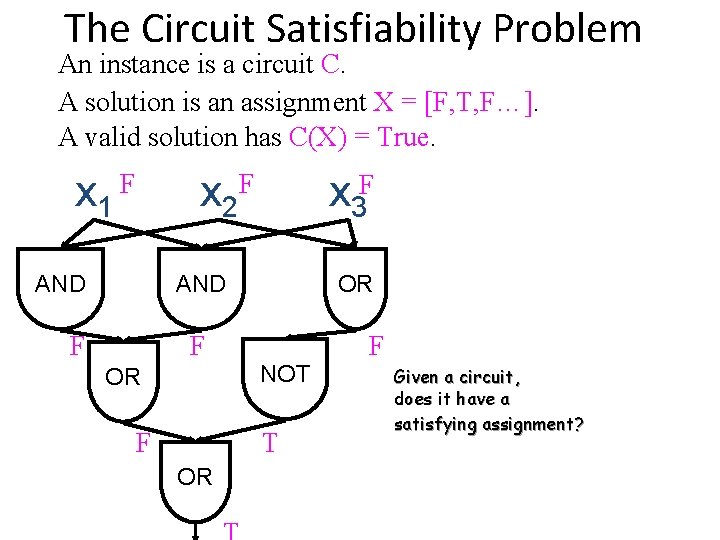
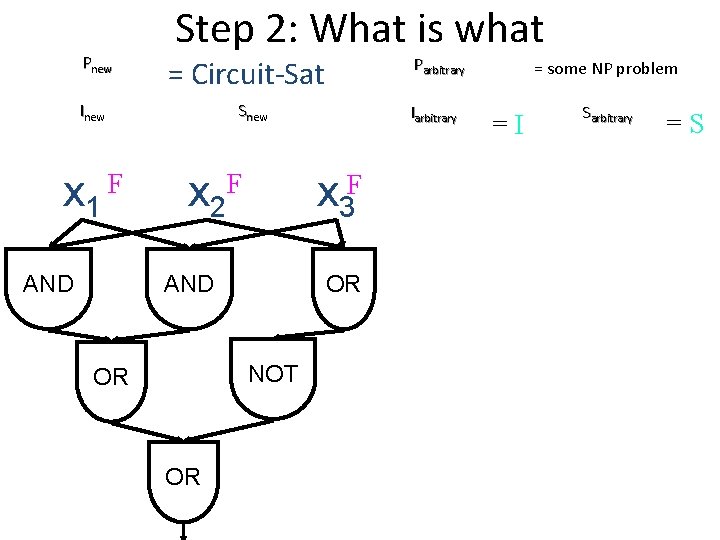
The Circuit Satisfiability Problem An instance is a circuit C. A solution is an assignment X = [F, T, F…]. C(X) evaluates to T or F. x 1 F x 2 T x 3 F AND F F OR NOT F OR T One bit output No feedback

The Circuit Satisfiability Problem An instance is a circuit C. A solution is an assignment X = [F, T, F…]. A valid solution has C(X) = True. x 1 F x 2 F x 3 F AND F F OR NOT T OR F Given a circuit, does it have a satisfying assignment?

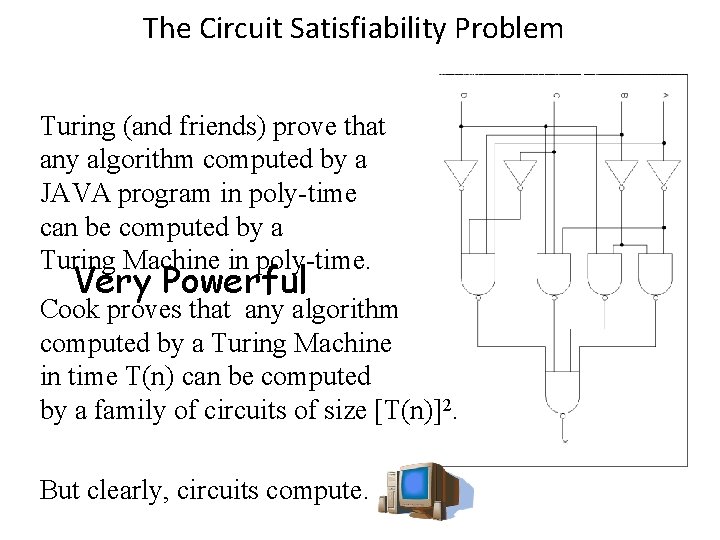
The Circuit Satisfiability Problem Turing (and friends) prove that any algorithm computed by a JAVA program in poly-time can be computed by a Turing Machine in poly-time. Very Powerful Cook proves that any algorithm computed by a Turing Machine in time T(n) can be computed by a family of circuits of size [T(n)]2. But clearly, circuits compute.

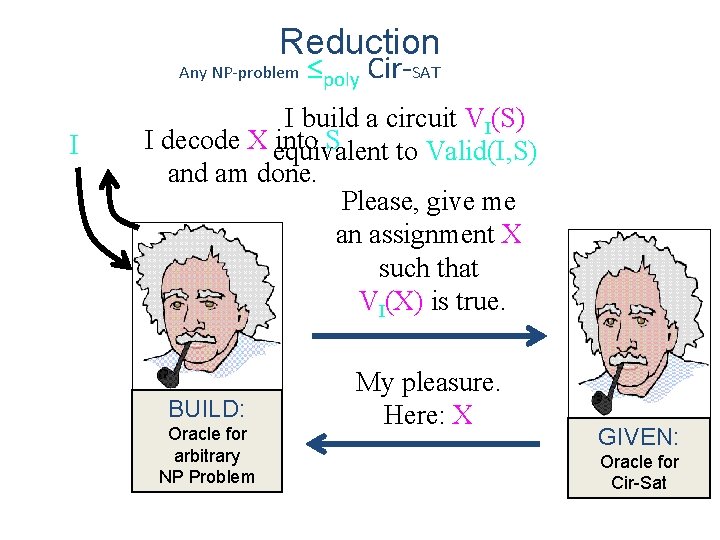
Reduction Any NP-problem ≤poly Cir-SAT I build a circuit VI(S) equivalent to Valid(I, S) I Please, give me a solution S such that VI(S) is true. BUILD: Oracle for arbitrary NP Problem Thanks for the circuit. But what is S? I can only find assignments. GIVEN: Oracle for Cir-Sat

Reduction Any NP-problem I ≤poly Cir-SAT I build a circuit VI(S) I decode X equivalent into S to Valid(I, S) and am done. Please, give me an assignment X such that VI(X) is true. BUILD: Oracle for arbitrary NP Problem My pleasure. Here: X GIVEN: Oracle for Cir-Sat

12 Step Program • Let's be more formal. • And flow the 12 steps.

Step 0: Cir-SAT NP • Design poly-time algorithm Valid. Cir-SAT(C, X) • which determines whether a given assignment X • is valid for a given circuit C. • Easy: Evaluate C(X).

Step 1: What to reduce it to Palg ≤poly Cir-Sat Choose a problem Pis NP-comp that is as similar to Cir-Sat as possible and that is already known to be NP-Complete. Have none. Any NP-problem ≤poly Cir-SAT We have a poly-time alg Valid(I, S) to test whether or not S is a valid solution for I.

Pnew Step 2: What is what Inew x 1 F AND Parbitrary = Circuit-Sat Snew x 2 F x 3 F AND OR NOT OR OR Iarbitrary = some NP problem =I Sarbitrary =S

Step 3: Direction of reduction & Code Given oracle for Cir-Sat, we need to be able to solve any NP-Complete problem. Parbitrary Cir-Sat

Step 4: Look for similarities x 1 F AND x 2 F x 3 F AND OR NOT OR OR S I ?

Step 5: Instance Map

Step 5: Instance Map I circuit We have a poly-time alg Valid(I, S) to test whether or not S is a valid solution for I. Let Validn(I, S) be a circuit: • I is a bit string representing an instance I. • S is a bit string representing a solution S. • Outputs T if S is an encoding of a valid solution of I. Eg: Clique G, k I S {u. v} E OR u S OR v S |S| k And over pairs of nodes

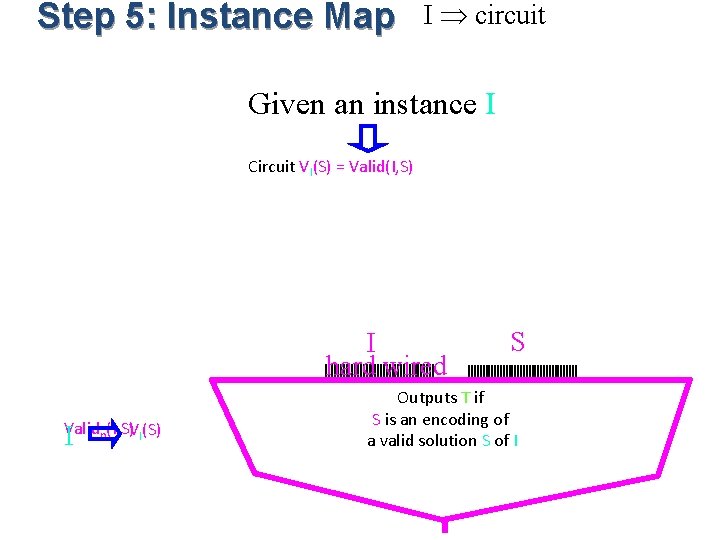
Step 5: Instance Map I circuit Given an instance I Circuit VI(S) = Valid(I, S) I hard wired Validn(I, S)VI(S) I S Outputs T if S is an encoding of a valid solution S of I

Step 6: Solution Map

Step 6: Solution Map S assignment X=[T, F, F, T] X is viewed as a bit string S representing a solution S. If X is not a bit string representing a solution then “what ever” I hard wired I VI(S) S Outputs T if S is an encoding of a valid solution S of I

Step 6: Solution Map S assignment X=[T, F, F, T] X is viewed as a bit string S representing a solution S I hard wired I VI(S) S Outputs T if S is an encoding of a valid solution S of I

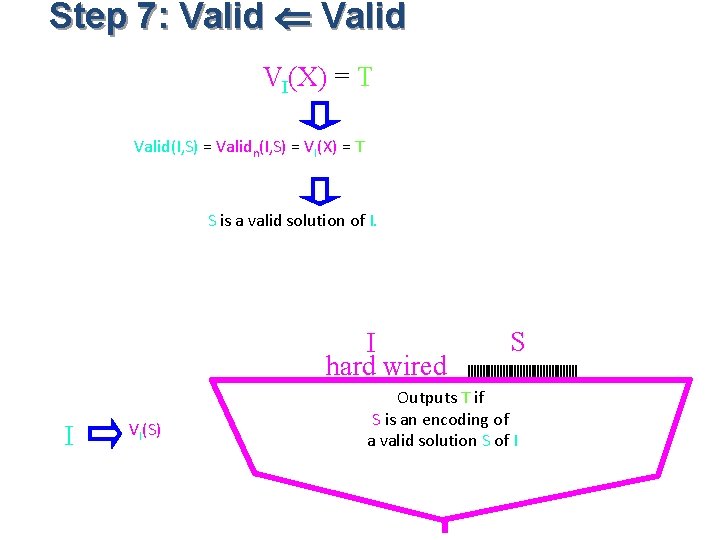
Step 7: Valid VI(X) = T Valid(I, S) = Validn(I, S) = VI(X) = T S is a valid solution of I. I hard wired I VI(S) S Outputs T if S is an encoding of a valid solution S of I

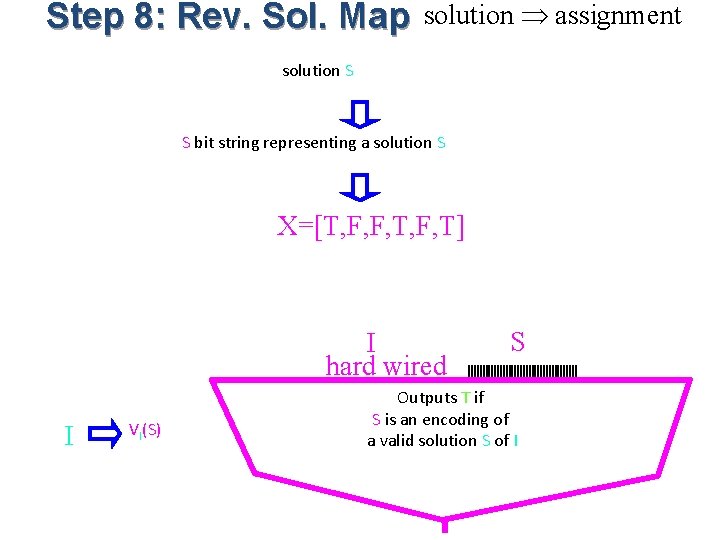
Step 8: Rev. Sol. Map solution assignment solution S S bit string representing a solution S X=[T, F, F, T] I hard wired I VI(S) S Outputs T if S is an encoding of a valid solution S of I

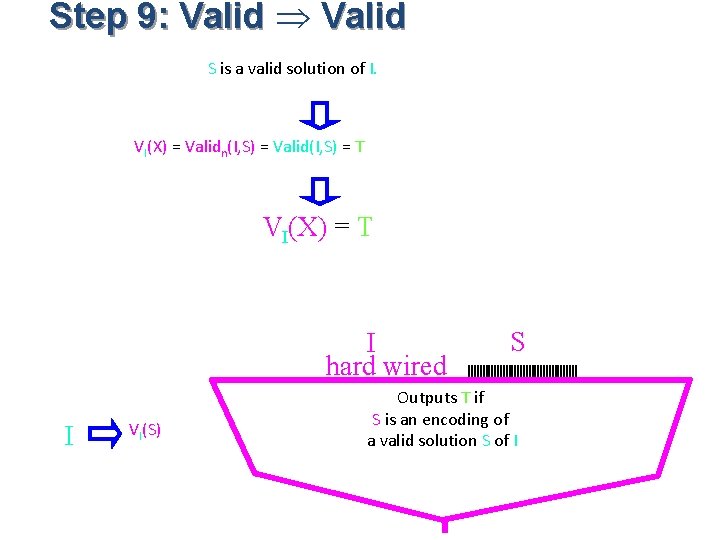
Step 9: Valid S is a valid solution of I. VI(X) = Validn(I, S) = Valid(I, S) = T VI(X) = T I hard wired I VI(S) S Outputs T if S is an encoding of a valid solution S of I

Reduction Any NP-problem ≤poly Cir-SAT I Yes/No i. e. S, S is a valid solution for I VI BUILD: Opt. problem satisfiable or not i. e. X, VI(X) GIVEN: Alg for circuit problem

Palg ≤poly Poracle or Palg Poracle 3 -Col ? Scheduling Graph Colouring Clique Independent Set Circuit Satisfiability Any NP-Problem

3 -Col Graph Col: Given graph G & k can G be coloured with k colours? 3 -Col: Given graph G can G be coloured with 3 colours? 3 -Col ≤poly Graph Col If you can decide whether you can colour with k colours, then you can decide whether you can colour with 3 colours. G, k C G C

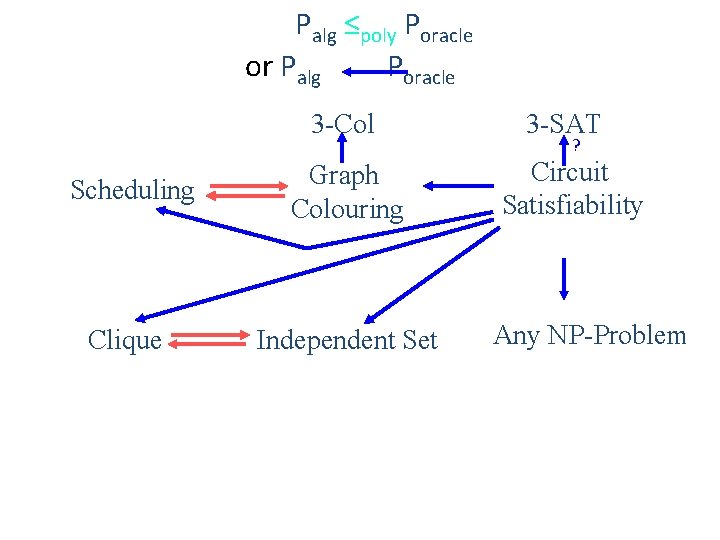
Palg ≤poly Poracle or Palg Poracle 3 -Col Scheduling Graph Colouring Clique Independent Set 3 -SAT ? Circuit Satisfiability Any NP-Problem

3 -SAT Cir Sat: Given circuit C does it have a satisfying assignment X? 3 -SAT: Given an expression: • A circuit consisting of a big AND of clauses • Each clause is the OR of at most 3 literals • Each literal is a variable or its negation. does it have a satisfying assignment X? FT F F T F xoryorz AND xorwora AND …

3 -SAT Cir Sat: Given circuit C does it have a satisfying assignment X? 3 -SAT: Given an expression: does it have a satisfying assignment X? 3 -Sat ≤poly Cir Sat If you can decide whether any circuit is satifiable, then you can decide whether a circuit that happens to be an expression is satisfiable. FT F F T F xoryorz AND xorwora AND …

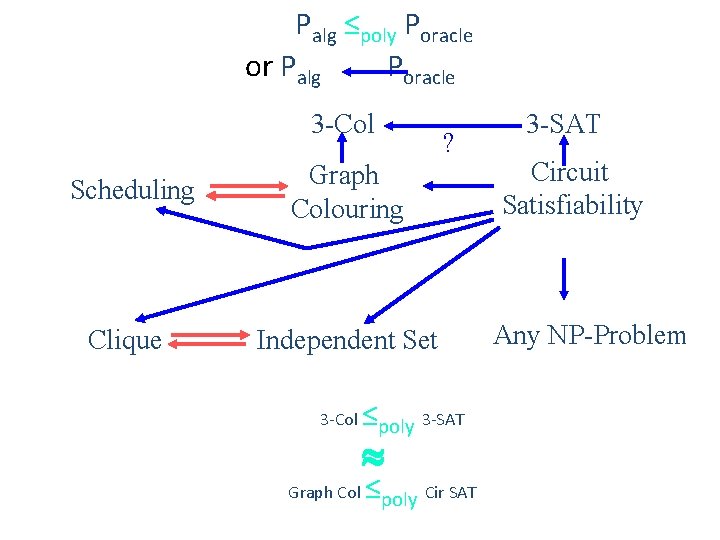
Palg ≤poly Poracle or Palg Poracle 3 -Col Scheduling Graph Colouring Clique Independent Set 3 -Col Graph Col ? ≤poly 3 -SAT » ≤poly Cir SAT 3 -SAT Circuit Satisfiability Any NP-Problem

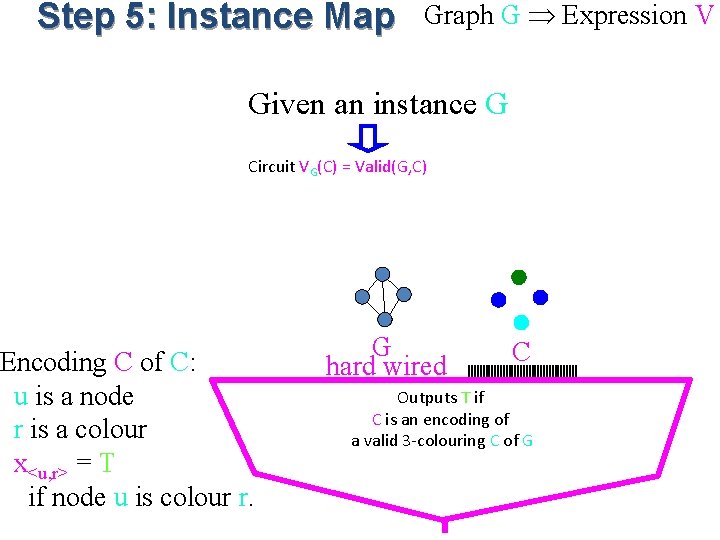
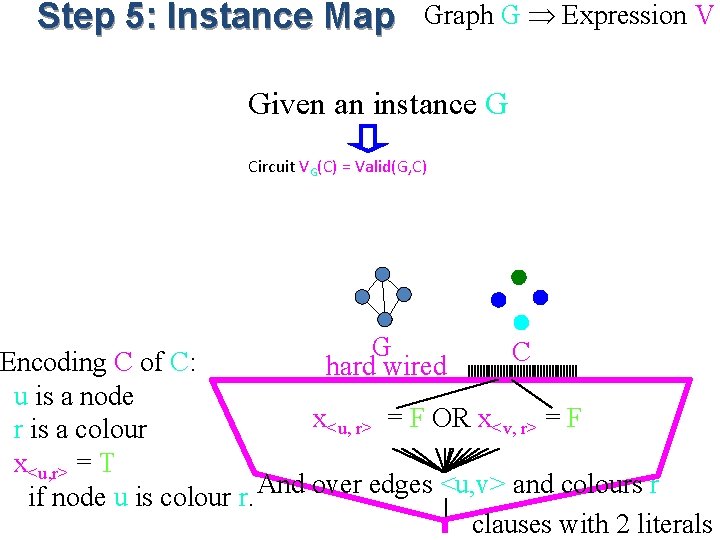
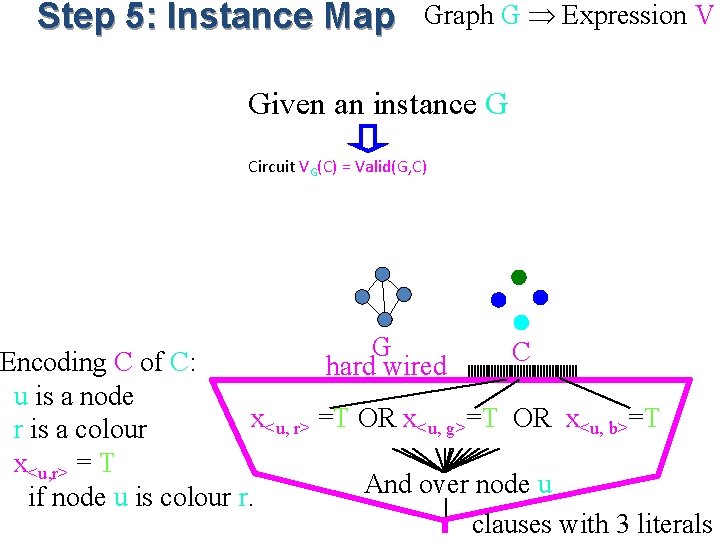
Step 5: Instance Map Graph G Expression V Given an instance G Circuit VG(C) = Valid(G, C) Encoding C of C: u is a node r is a colour x<u, r> = T if node u is colour r. G hard wired C Outputs T if C is an encoding of a valid 3 -colouring C of G

Step 5: Instance Map Graph G Expression V Given an instance G Circuit VG(C) = Valid(G, C) G hard wired C Encoding C of C: u is a node x<u, r> = F OR x<v, r> = F r is a colour x<u, r> = T if node u is colour r. And over edges <u, v> and colours r clauses with 2 literals

Step 5: Instance Map Graph G Expression V Given an instance G Circuit VG(C) = Valid(G, C) G hard wired C Encoding C of C: u is a node x<u, r> =T OR x<u, g>=T OR x<u, b>=T r is a colour x<u, r> = T And over node u if node u is colour r. clauses with 3 literals