UNIT II Shear Force Diagrams and Bending Moment

UNIT - II Shear Force Diagrams and Bending Moment Diagrams Lecture Number -1 Prof. M. J. Naidu Mechanical Engineering Department Smt. Kashibai Navale College of Engineering, Pune-41 Strength of Materials

Introduction Ø SFD and BMD used for analysis of Beam. Ø SFD- Variation of the shear force along the length. Ø BMD- Variation of the bending moment along the length. Ø Value of Shear Force use to calculate shear stress Ø Value of Bending moment use to calculate Bending Stress

Types of Load Concentrated Load Uniform Varying Load Applied Couple

Types of Support Fixed or Build in Roller Pinned or Hingged

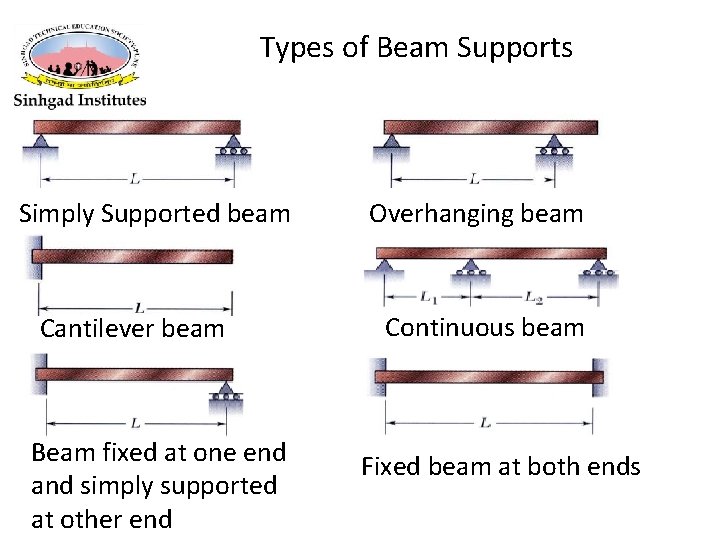
Types of Beam Supports Simply Supported beam Cantilever beam Beam fixed at one end and simply supported at other end Overhanging beam Continuous beam Fixed beam at both ends

Sign Convention for Shear Force When moves from left to right Direction of Shear force Positive Shear force Negative Shear force

Relation between Load, SFD and BMD

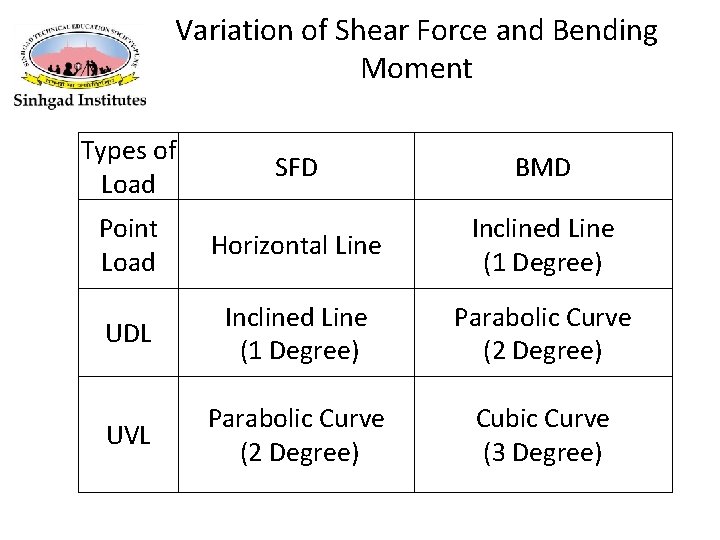
Variation of Shear Force and Bending Moment Types of Load SFD BMD Point Load Horizontal Line Inclined Line (1 Degree) UDL Inclined Line (1 Degree) Parabolic Curve (2 Degree) UVL Parabolic Curve (2 Degree) Cubic Curve (3 Degree)

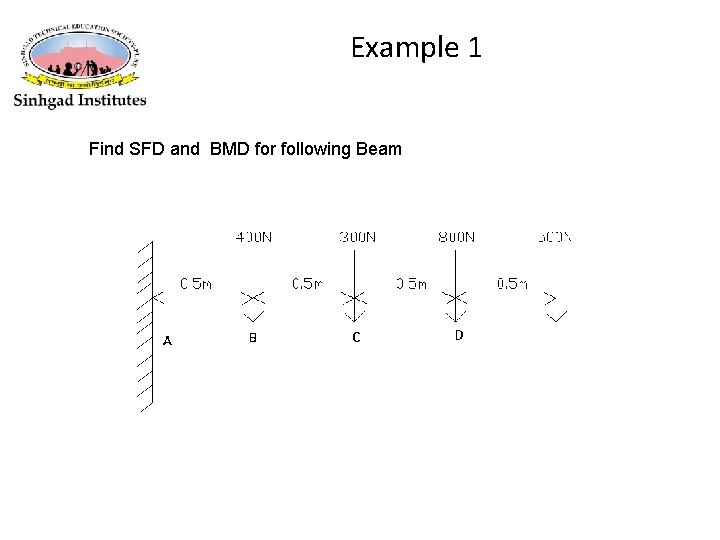
Example 1 Find SFD and BMD for following Beam

Reaction at A is sum of all forces at right side of A RA =400+300+800+500 = 2000 N Shear Force To find shear force start from left side Shear force at A (Just left) = 0 N Shear force at A (Just right) = 2000 N Shear force at B (Just left) = 2000 N Shear force at B(Just right) = 2000 -400= 1600 N Shear force at C (Just left) = 1600 N Shear force at C (Just right) = 1600 -300= 1300 N Shear force at D (Just left) = 1300 N Shear force at D (Just right) = 1300 -800= 500 N Shear force at E (Just left) = 500 N Shear force at E (Just right) = 500 -500 N= 0 N

Bending moment Starting from free end BME= 0 Nm BMD= -500*0. 5= -250 Nm BMC= -800*0. 5 -500*1= -900 Nm BMB= -300*0. 5 -800*1 -500*1. 5= -1700 Nm BMA= -400*0. 5 -300*1 -800*1. 5 -500*2= -2000 Nm

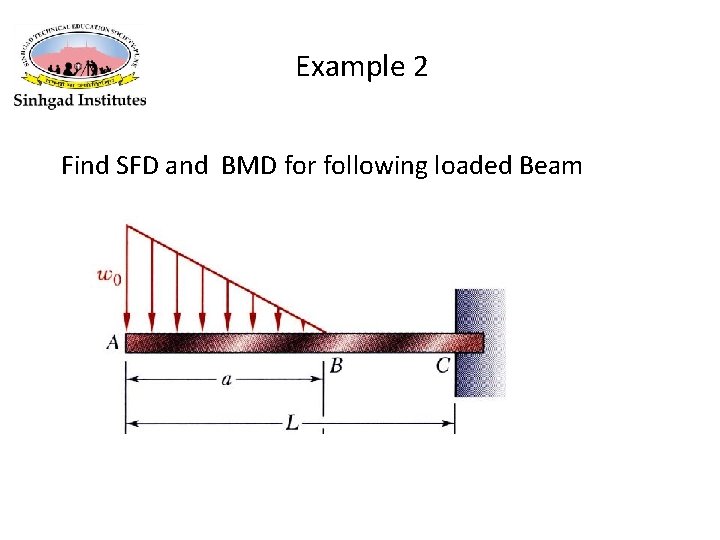
Example 2 Find SFD and BMD for following loaded Beam

HINTS Take the entire beam as a free body. Determine the reactions at C. Apply the relationship between shear and load Develop the shear diagram. . Apply the relationship between bending moment and shear • Develop the bending moment diagram. • • •

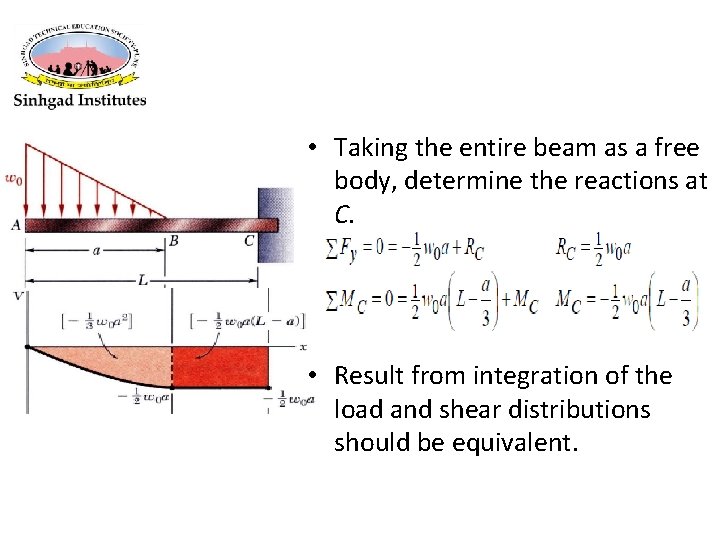
• Taking the entire beam as a free body, determine the reactions at C. • Result from integration of the load and shear distributions should be equivalent.

• Apply the relationship between shear and load to develop the shear diagram. • No change in shear between Band C. • Compatible with free body analysis

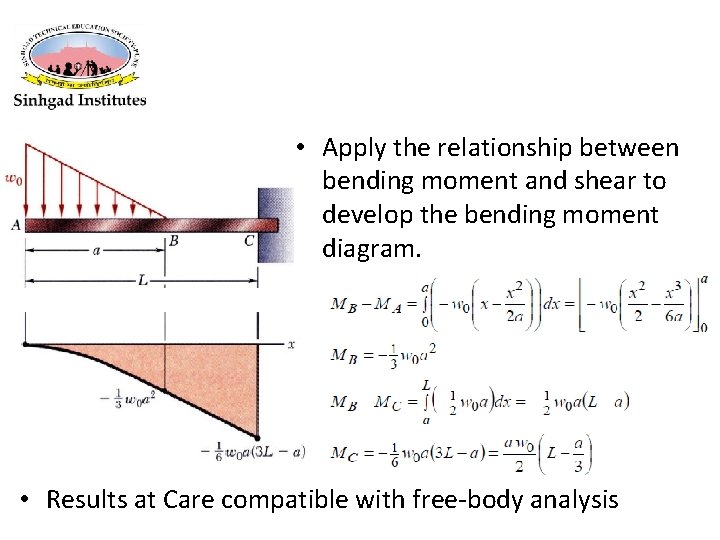
• Apply the relationship between bending moment and shear to develop the bending moment diagram. • Results at Care compatible with free-body analysis

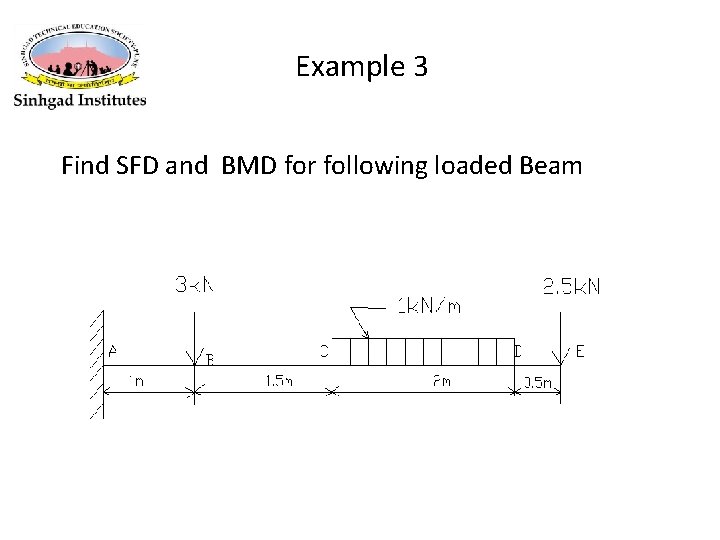
Example 3 Find SFD and BMD for following loaded Beam

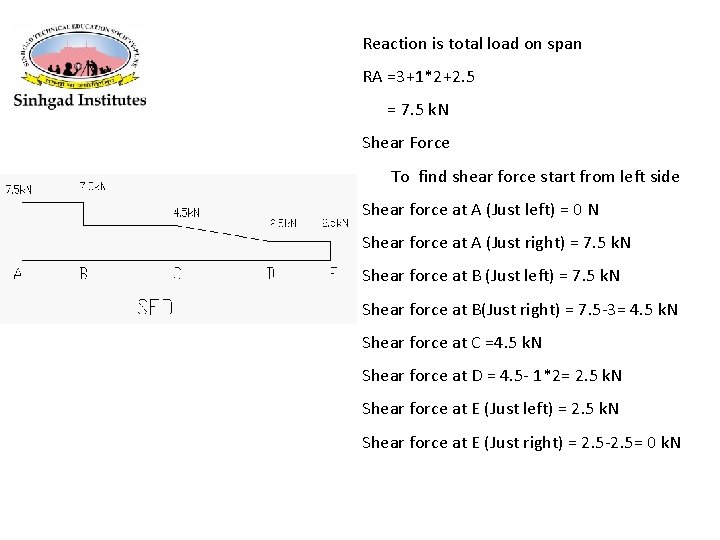
Reaction is total load on span RA =3+1*2+2. 5 = 7. 5 k. N Shear Force To find shear force start from left side Shear force at A (Just left) = 0 N Shear force at A (Just right) = 7. 5 k. N Shear force at B (Just left) = 7. 5 k. N Shear force at B(Just right) = 7. 5 -3= 4. 5 k. N Shear force at C =4. 5 k. N Shear force at D = 4. 5 - 1*2= 2. 5 k. N Shear force at E (Just left) = 2. 5 k. N Shear force at E (Just right) = 2. 5 -2. 5= 0 k. N

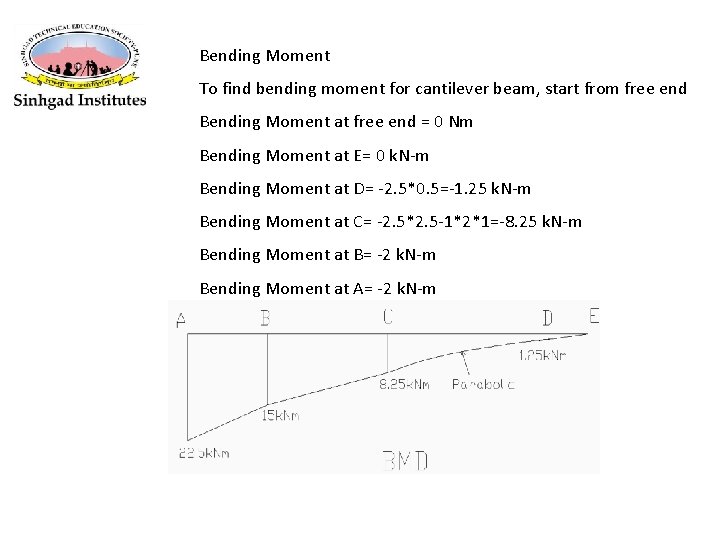
Bending Moment To find bending moment for cantilever beam, start from free end Bending Moment at free end = 0 Nm Bending Moment at E= 0 k. N-m Bending Moment at D= -2. 5*0. 5=-1. 25 k. N-m Bending Moment at C= -2. 5*2. 5 -1*2*1=-8. 25 k. N-m Bending Moment at B= -2 k. N-m Bending Moment at A= -2 k. N-m

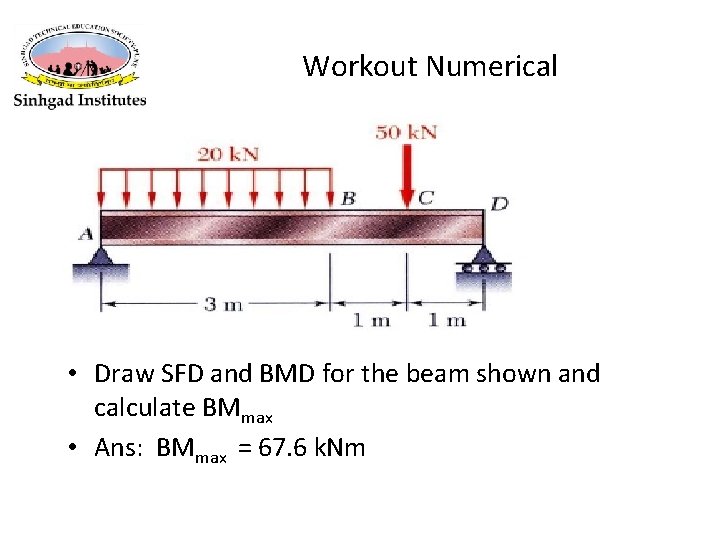
Workout Numerical • Draw SFD and BMD for the beam shown and calculate BMmax • Ans: BMmax = 67. 6 k. Nm