UNIT II Queue Syllabus Contents Concept of queue

UNIT II Queue

Syllabus Contents • Concept of queue as ADT • Implementation using linked and sequential organization. – linear – circular queue • Concept – multiqueue – double ended queue – priority queue • Applications of queue 2

Abstract Data Type • What does ‘abstract’ mean? • From Latin: to ‘pull out’—the essentials – To defer or hide the details – Abstraction emphasizes essentials and defers the details, making engineering artifacts easier to use • I don’t need a mechanic’s understanding of what’s under a car’s hood in order to drive it – What’s the car’s interface? – What’s the implementation? 3

ADT = properties + operations • An ADT describes a set of objects sharing the same properties and behaviors – The properties of an ADT are its data (representing the internal state of each object • double d; -- bits representing exponent & mantissa are its data or state – The behaviors of an ADT are its operations or functions (operations on each instance) • sqrt(d) / 2; //operators & functions are its behaviors • Thus, an ADT couples its data and operations – OOP emphasizes data abstraction 4

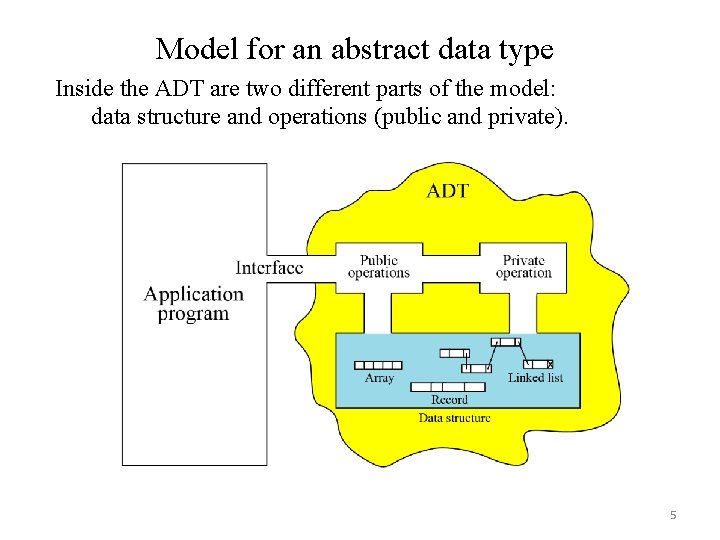
Model for an abstract data type Inside the ADT are two different parts of the model: data structure and operations (public and private). 5

Definition of a Queue • A queue is a data structure that models/enforces the firstcome first-serve order, or equivalently the first-in first-out (FIFO) order. • That is, the element that is inserted first into the queue will be the element that will deleted first, and the element that is inserted last is deleted last. • A waiting line is a good real-life example of a queue. (In fact, the British word for “line” is “queue”. ) 6

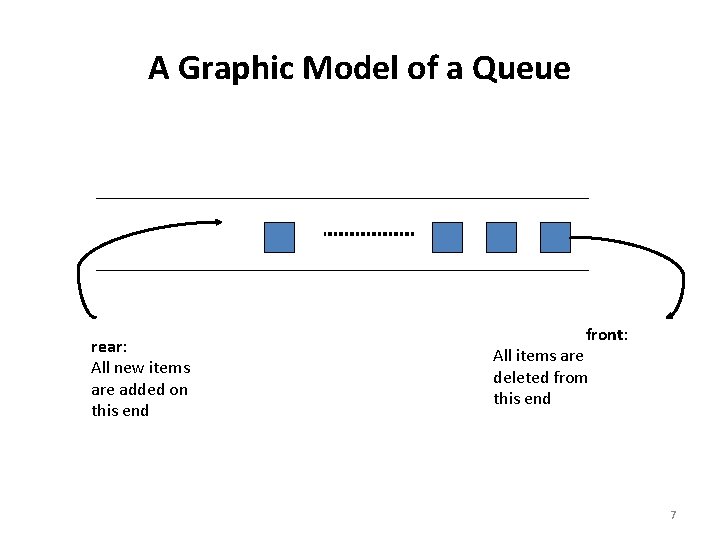
A Graphic Model of a Queue rear: All new items are added on this end front: All items are deleted from this end 7

Operations on Queues • Insert(item): (also called enqueue) – It adds a new item to the rear of the queue • Remove( ): (also called delete or dequeue) – It deletes the front item of the queue, and returns to the caller. If the queue is already empty, this operation returns NULL • getfront( ): – Returns the value in the front element of the queue • getrear( ): – Returns the value in the rear element of the queue • is. Empty( ) – Returns true if the queue has no items • is. Full() – Returns true if the queue is full • size( ) – Returns the number of items in the queue 8

Queue ADT objects: a finite ordered list with zero or more elements. methods: for all queue Queue, item element, max_ queue_ size positive integer Queue create. Q(max_queue_size) : : = create an empty queue whose maximum size is max_queue_size Boolean is. Full. Q(queue, max_queue_size) : : = if(number of elements in queue == max_queue_size) return TRUE else return FALSE 9

Queue ADT (cont’d) Queue Enqueue(queue, item) : : = if (Is. Full. Q(queue)) queue_full else insert item at rear of queue and return queue Boolean is. Empty. Q(queue) : : = if (queue ==Create. Q(max_queue_size)) return TRUE else return FALSE Element dequeue(queue) : : = if (Is. Empty. Q(queue)) return else remove and return the item at front of queue. 10

Array-based Queue Implementation • As with the array-based stack implementation, the array is of fixed size – A queue of maximum N elements • Slightly more complicated – Need to maintain track of both front and rear Implementation 1 Implementation 2 11

FIFO queue ADT interface template <class Item> class QUEUE { private: // Implementation-dependent code public: QUEUE(int); int empty(); void put(Item); Item get(); int full(); }; 12

Linear Queue Operation • Explain all operations with example 13

Linear queue array implementation template <class Item> class QUEUE { private: Item *q; int N, front, rear; public: QUEUE(int max. N) { q = new Item[max. N+1]; N = max. N+1; front = 0; rear = 0; } int empty() const { return front % N == rear; } void put(Item item) { q[rear++] = item; rear = rear % N; } Item get() { front = front % N; return q[front++]; } int full() const { return rear == max. N; } }; If front = rear, then empty; if put would make them equal, then full. Array is 1 larger to allow checks. 14

Circular Queue Operations EMPTY QUEUE [2] [1] [2] J 2 [0] [3] [5] front = 0 rear = 0 [4] J 3 [0]J 1 [3] [5] [4] front = 0 rear = 2 15

FULL QUEUE [1] [2] J 2 [0] J 3 J 1 J 4 J 6 [4] front =0 rear = 4 [2] J 9 [3][0]J 7 J 10 J 6 J 5 [5] [1] J 8 [3] J 5 [5] [4] front =4 rear =2 16

Circular Queue Operations • Explain all operations with example 17

Circular queue array implementation template <class Item> class QUEUE { private: Item *q; int N, front, rear; public: QUEUE(int max. N) { q = new Item[max. N]; N = max. N; front = max. N; rear = 0; } int empty() const { return front % N == rear; } void put(Item item) { q[rear++] = item; rear = rear % N; } Item get() { front = front % N; return q[front++]; } int full() const { return (rear+1)%N == front; } }; If front = rear, then empty; if put would make them equal, then full. Array is 1 larger to allow checks. 18

Linear Queue using Linked List • Explain all operations with example 19

Linear queue linked-list implementation template <class Item> class QUEUE { private: struct node { Item item; node* next; node(Item x) { item = x; next = 0; } }; typedef node *link; link head, tail; public: QUEUE(int) { head = 0; } int empty() const { return head == 0; } void put(Item x) { link t = tail; tail = new node(x); if (head == 0) head = tail; else t->next = tail; } Item get() { Item v = head->item; link t = head->next; delete head; head = t; return v; } }; 20

Circular Queue using Linked List • Explain all operations with example 21

Circular queue linked-list implementation template <class Item> class QUEUE { private: struct node { Item item; node* next; node(Item x) { item = x; next = 0; } }; typedef node *link; link head, tail; public: QUEUE(int) { head = 0; } int empty() const { return head == 0; } void put(Item x) { link t = tail; tail = new node(x); if (head == 0) { head = tail; head->next=head; } else { t->next = tail; tail->next = head; } } Item get() { Item v = head->item; link t = head->next; delete head; head = t; tail->next = head; return v; } }; 22

Algorithm Analysis • • • enqueue. O(1) dequeue O(1) size O(1) is. Empty O(1) is. Full O(1) 23

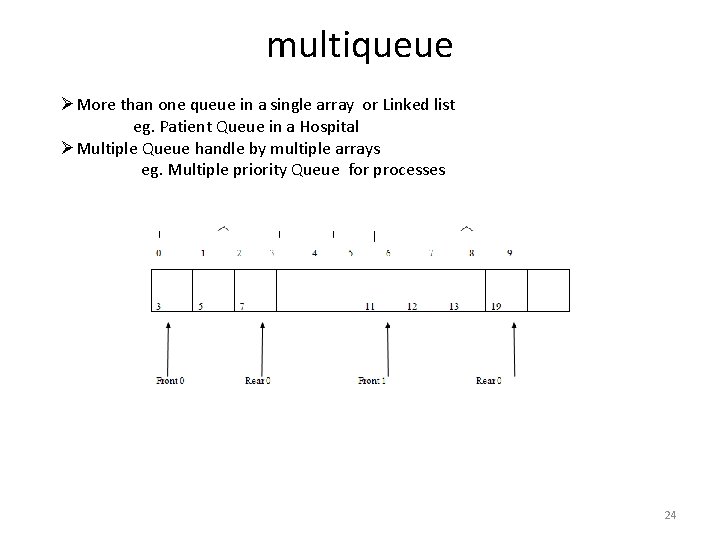
multiqueue ØMore than one queue in a single array or Linked list eg. Patient Queue in a Hospital ØMultiple Queue handle by multiple arrays eg. Multiple priority Queue for processes 24

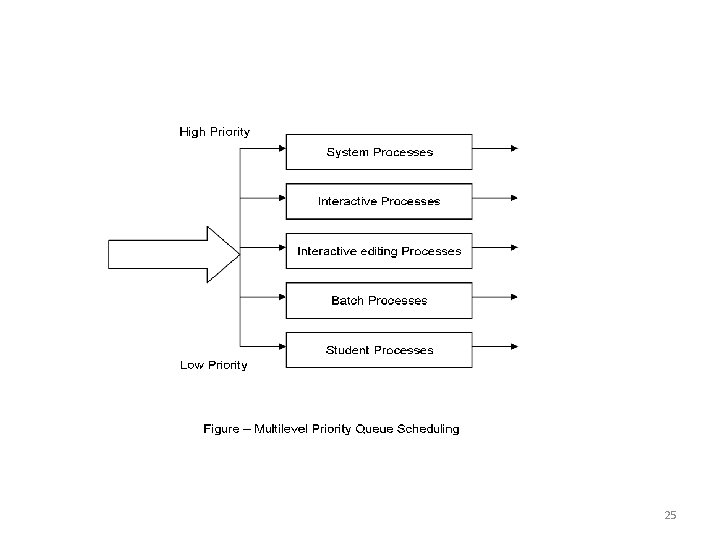
25

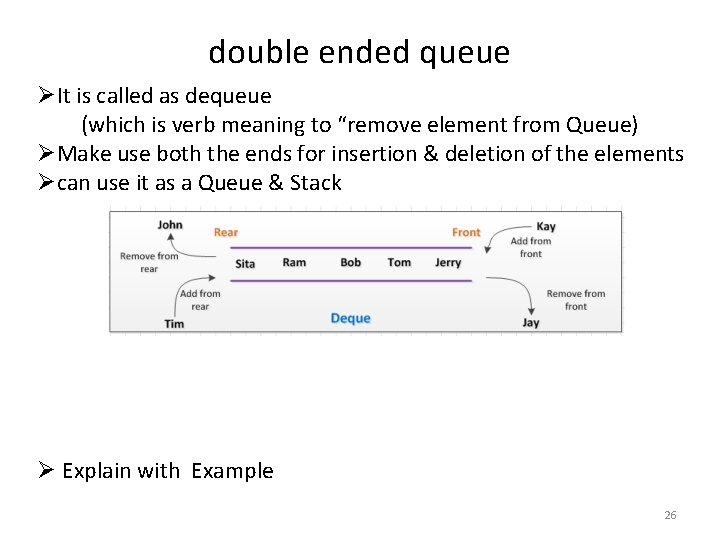
double ended queue ØIt is called as dequeue (which is verb meaning to “remove element from Queue) ØMake use both the ends for insertion & deletion of the elements Øcan use it as a Queue & Stack Ø Explain with Example 26

Priority queue Ø Elements associated with specific ordering Ø Two types ⁻ Ascending priority queue ⁻ Descending priority queue Ø Application ⁻ Priority scheduling in OS ⁻ N/W communication 27

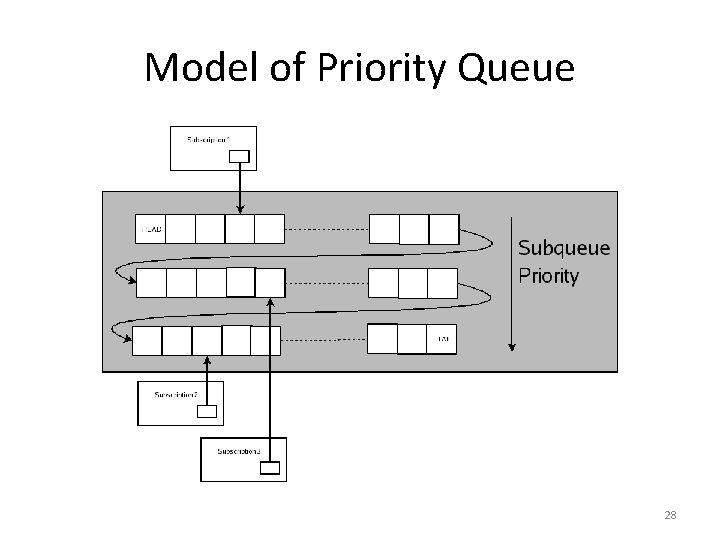
Model of Priority Queue 28

Implementation of Priority Queue template <class Item> class QUEUE { private: struct node { Item item; int priority; node* next; node(Item x) { item = x; next = 0; } }; typedef node *link; link head; public: QUEUE(int) { head = 0; } int empty() const { return head == 0; } item get() { item patient = head->item ; head = head->next; return patient; } 29

Implementation of Priority Queue ( continue…) void put(Item x int p) { link temp , prev , n. Patient = new node(x); n. Patient->priority = p; if (head == 0) head = n. Patient; else { temp = prev = head; while( temp->priority >= p & temp != 0) { prev = temp; temp = temp->next; } if( temp == head ) { n. Patient->next = head ; head = n. Patient; } else { prev->next = n. Patient; n. Patient->next = temp; } } }; 30

Queues Applications • An electronic mailbox is a queue – The ordering is chronological (by arrival time) • A waiting line in a store, at a service counter, on a one-lane road, Patient in a Hospital • Applications related to Computer Science – Threads – Job scheduling (e. g. Round-Robin algorithm for CPU allocation) 31

Thank You ! 32