Unit II Polygons Clipping Ordered set of vertices

Unit II: Polygons & Clipping

� Ordered set of vertices (points) ◦ Usually counter-clockwise � Two consecutive vertices define an edge � Left side of edge is inside � Right side is outside � Last vertex implicitly connected to first 22

� Convex : In a convex polygon, any line segment joining any two inside points lies inside the polygon. � Concave: In a concave polygon, a line segment connecting any two points may or may not lie inside the polygon. 3

□ To determine whether point is inside or outside the polygon, following tests are done: 1. Odd-Even Method 2. Winding number Method 4

Odd-Even Method : 1. 2. 3. Draw a line between a point P to be tested for inside or outside and a point which is surely outside the polygon. Count the number of intersections by the line with edges of the polygon. If the number of polygon edges crossed by this line is odd then P is an interior point. Else P is an exterior point 5

Odd-Even Method : Special Cases: When line passing through the vertex of the polygon, then a) b) c) Check other end points of the polygon edges which meet at this point. If these points lie on the same side of line then intersection point counts as an even count. But if these points lie on opposite side of line then intersection point counts as odd count. 6

Odd-Even Method : Example: 1. For Point A: No of intersection is 1 ie odd So Point A is Inside the polygon. 2. For Point D: No of intersection is 2 ie Even So Point D is Outside the polygon. 3. For Point B: Line is passing through vertex, So check polygon edges. Both polygon edges are at opposite to the line so consider intersection only once. ie odd So Point B is Inside the polygon. 4. For Point C: Line is passing through vertex, So check polygon edges. Both polygon edges are at same side of the line so consider intersection twice. ie even So Point C is Inside the polygon. 7

Winding Number Method: □ 1. 2. Counts the number of times the polygon edges wind around a particular point in the counterclockwise direction. This count is called the winding number, and the interior points of a two- dimensional object are defined to be those that have a nonzero value for the winding number. Initializing the winding number to 0. Imagine a line drawn from any position P to a distant point beyond the coordinate extents of the object. 8

Winding Number Method: 3. Count the number of edges that cross the line in each direction. We add 1 to the winding number every time we intersect a polygon edge that crosses the line from right to left, and we subtract 1 every time we intersect an edge that crosses from left to right. 4. If the winding number is nonzero, then P is defined to be an interior point Else P is taken to be an exterior point. 9

10

• This algorithm is used to fill polygon having boundary in single color. • Algorithm starts from seed point and start filling towards the boundary. As the boundary is specified in a single color, the fill algorithm proceeds outward pixel by pixel until the boundary color is encountered. • The inputs of the this algorithm are: • • • Coordinates of the interior point (x, y) Fill Color Boundary Color 11

• Algorithm Starts from point(x, y), the algorithm tests neighboring pixels to determine whether they are of the boundary color and fill color. If not, they are painted with the fill color, and their neighbors are tested. This process continues until all pixels up to the boundary have been tested. • There are two methods for proceeding to neighboring pixels from the current test position: 12

1. The 4 -connected method. 2. The 8 -connected method. Department of Computer Engineering, DYPCOE, Akurdi 13

void boundary. Fill 4 (int x, int y, int fill. Color, int boundary. Color) { interior. Color = get. Pixel (x, y); if ( (interior. Color != border. Color) && (interior. Color != fill. Color) ) { set. Pixel (x, y); // set color of pixel to fill. Color boundary. Fill 4 (x + 1, y, fill. Color, boundary. Color); boundary. Fill 4 (x - 1, y, fill. Color, boundary. Color); boundary. Fill 4 (x, y + 1, fill. Color, boundary. Color); boundary. Fill 4 (x, y - 1, fill. Color, boundary. Color); } } 14 14

□ When polygon has boundary in many colors then flood-fill algorithm is used to fill the polygon. Department of Computer Engineering, DYPCOE, Akurdi 15

• • • Algorithm starts from a specified interior point (x, y), check its color. If it is in old color then assign new color to that pixel. Check neighboring pixels for color. Using either a 4 -connected or 8 -connected approach, we then step through pixel positions until all interior points have been repainted. Department of Computer Engineering, DYPCOE, Akurdi 16

void flood. Fill 4 (int x, int y, int fill. Color, interior. Color) { int color; /* set current color to fill. Color, then perform following operations. */ Color = get. Pixel (x, y); if (color = interior. Color) { set. Pixel (x, y); // set color of pixel to fill. Color flood. Fill 4 (x + 1, y, fill. Color, interior. Color); flood. Fill 4 (x - 1, y, fill. Color, interior. Color); flood. Fill 4 (x, y + 1, fill. Color, interior. Color); flood. Fill 4 (x, y - 1, fill. Color, interior. Color); } } Department of Computer Engineering, DYPCOE, Akurdi 17

� Object Model: object with dimensions � Image Model : image of object � Object space : object model is stored in object space. � Image Space : image is viewed Department of Computer Engineering, DYPCOE, Akurdi 18

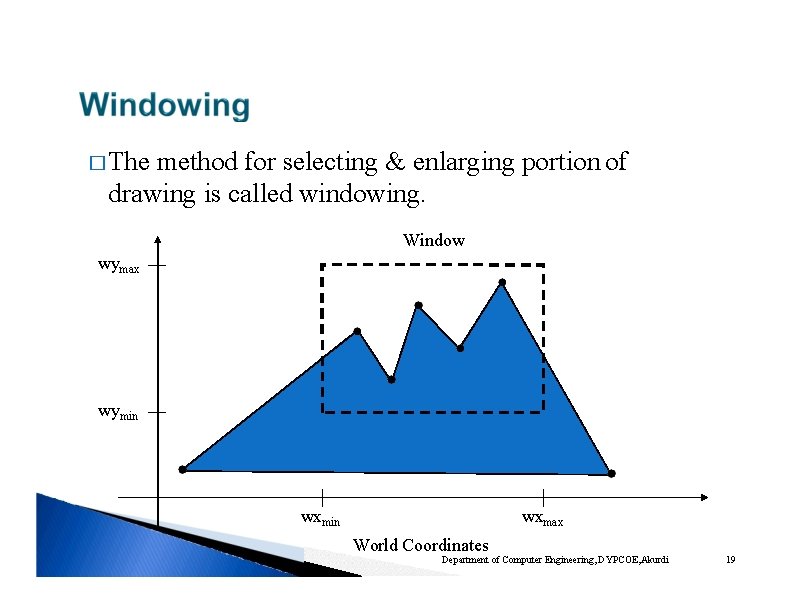
� The method for selecting & enlarging portion of drawing is called windowing. Window wymax wymin wxmax World Coordinates Department of Computer Engineering, DYPCOE, Akurdi 19

� Because drawing things to a display takes time we clip everything outside the window Window wymax wymin wxmax World Coordinates Department of Computer Engineering, DYPCOE, Akurdi 20

� The technique for not showing that part of drawing which one is not interested in is called clipping P 4 Window wymax P 2 P 6 P 3 P 1 P 5 P 7 P 9 P 8 wymin P 10 wxmin wxmax 21

22

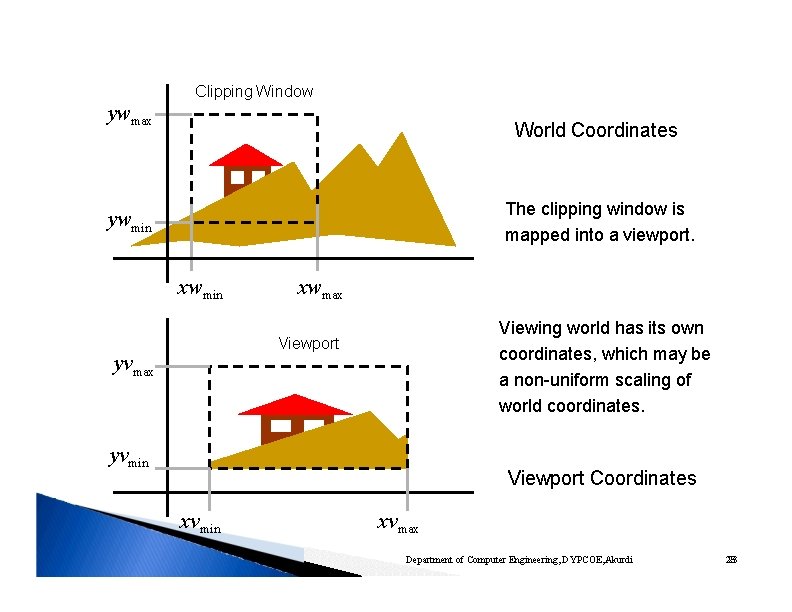
ywmax Clipping Window World Coordinates The clipping window is mapped into a viewport. ywmin xwmax Viewing world has its own coordinates, which may be a non-uniform scaling of world coordinates. Viewport yvmax yvmin Viewport Coordinates xvmin xvmax Department of Computer Engineering, DYPCOE, Akurdi 23 23

Department of Computer Engineering, DYPCOE, Akurdi 24 24

� Translation ◦ Object is translated until lower left corner is at origin � Scaling ◦ Object and window are scaled until window has the dimensions of the viewport � Translation ◦ Move the viewport to its correct position on the screen. Department of Computer Engineering, DYPCOE, Akurdi 25 25

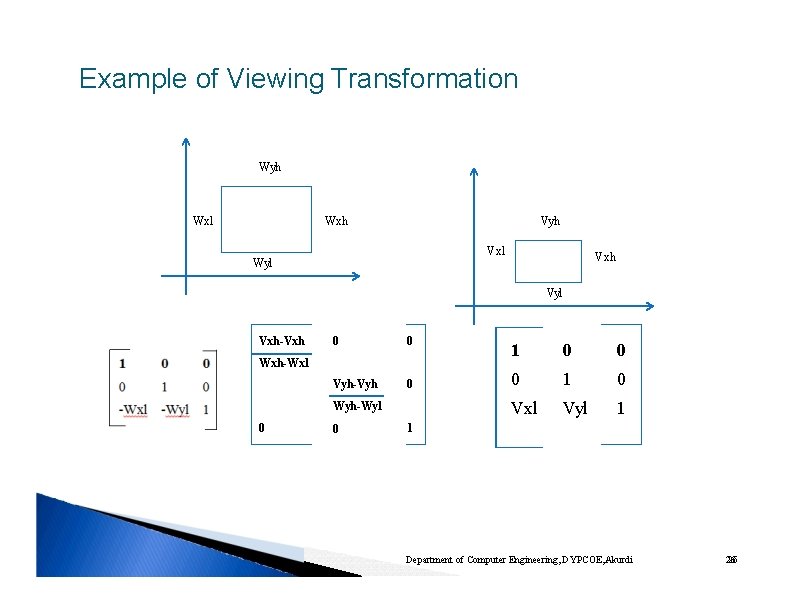
Example of Viewing Transformation Wyh Wxl Vyh Wxh Vxl Wyl Vxh Vyl Vxh-Vxh 0 0 Vyh-Vyh 0 Wxh-Wxl Wyh-Wyl 0 0 1 0 Vxl Vyl 1 1 Department of Computer Engineering, DYPCOE, Akurdi 26 26

27

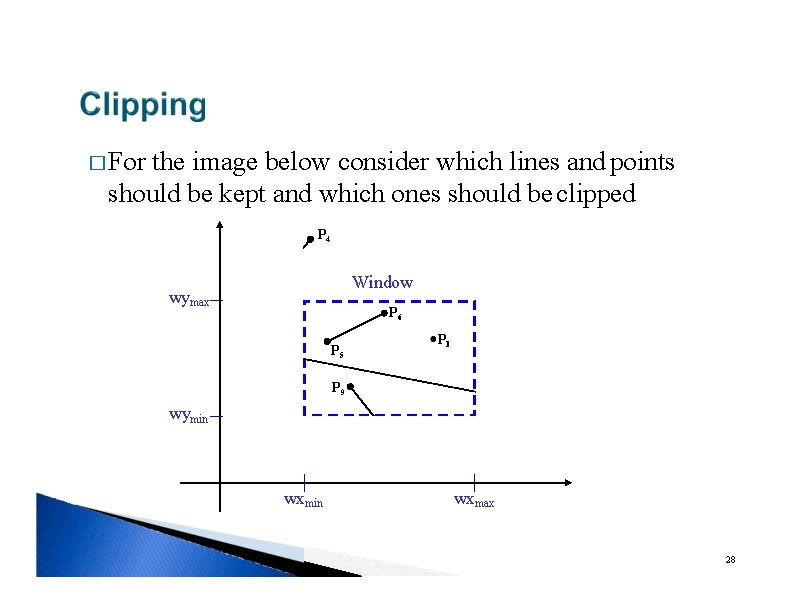
� For the image below consider which lines and points should be kept and which ones should be clipped P 4 Window wymax P 2 P 6 P 3 P 1 P 5 P 7 P 9 P 8 wymin P 10 wxmin wxmax 28

�An efficient line clipping algorithm �The key advantage of the algorithm is that it reduces the number of line intersections that must be calculated 29

� World space is divided into regions based on the window boundaries ◦ Each region has a unique four bit region code ◦ Region codes indicate the position of the regions with respect to the window 1001 3 2 1 above below right Region Code Legend 0 left 0001 0101 1000 0000 Window 0100 1010 0110 30

� Every end-point is labelled with the appropriate region code P 11 [1010] P 4 [1000] Window wymax P 6 [0000] P 3[0001] P 12 [0010] P 5 [0000] P 7 [0001] P 9 [0000] wymin P 13 [0101] wxmin P 8 [0010] P 10 [0100] P 14 [0110] wxmax 31

�Lines that cannot be identified as completely inside or outside the window may or may not cross the window interior �These lines are processed as follows: ◦ Compare an end-point outside the window to a boundary (choose any order in which to consider boundaries e. g. left, right, bottom, top) and determine how much can be discarded ◦ If the remainder of the line is entirely inside or outside the window, retain it or clip it respectively 32

◦ Otherwise, compare the remainder of the line against the other window boundaries ◦ Continue until the line is either discarded or a segment inside the window is found � We can use the region codes to determine which window boundaries should be considered for intersection ◦ To check if a line crosses a particular boundary we compare the appropriate bits in the region codes of its end-points ◦ If one of these is a 1 and the other is a 0 then the line crosses the boundary 33

� Consider the line P 9 to P 10 below ◦ Start at P 10 Window ◦ From the region codes wymax of the two end-points we know the line doesn’t cross the left or right P [0000] boundary wymin P ’ [0000] ◦ Calculate the P [0100] intersection of the line with the wxmin wxmax bottom boundary to generate point P 10’ ◦ The line P 9 to P 10’ is completely inside the window so is retained 9 10 10 34

� Consider the line P 3 to P 4 below ◦ Start at P 4 ◦ From the region codes of the two end-points we know the line crosses the left boundary so calculate the intersection point to generate P 4’ ◦ The line P 3 to P 4’ is completely outside the window so is clipped P 4’ [1001] wymax P 4 [1000] Window P 3 [0001] wymin wxmax 35

� Consider the line P 7 to P 8 below ◦ Start at P 7 ◦ From the two region codes of the two end-points we know the line crosses the left boundary so calculate the intersection point to generate P 7’ Window wymax P 7’ [0000] P 7 [0001] wymin wxmin P 8 [0010] P 8’ [0000] wxmax 36

� Consider the line P 7’ to P 8 ◦ Start at P 8 ◦ Calculate the intersection with the right boundary to generate P 8’ ◦ P 7’ to P 8’ is inside the window so is retained Window wymax P 7’ [0000] P 7 [0001] wymin wxmin P 8 [0010] P 8’ [0000] wxmax 37

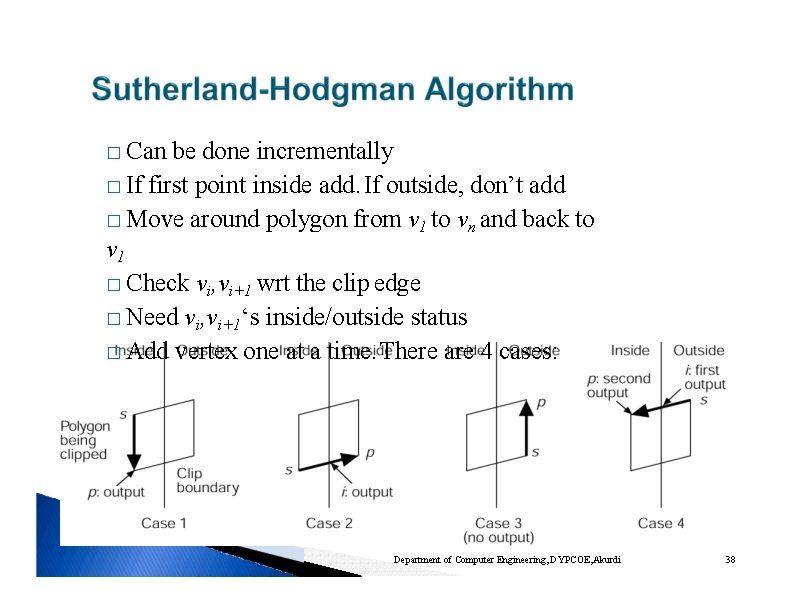
� Can be done incrementally � If first point inside add. If outside, don’t add � Move around polygon from v 1 to vn and back to v 1 � Check vi, vi+1 wrt the clip edge � Need vi, vi+1‘s inside/outside status � Add vertex one at a time. There are 4 cases: Department of Computer Engineering, DYPCOE, Akurdi 38

Sutherland-Hodgman Algorithm �For each polygon P P’ = P ◦ For each clipping edge (there are 4) { �Clip polygon P’ to clipping edge �For each edge in polygon P’ �Check clipping cases (there are 4) �Case 1 : Output vi+1 �Case 2 : Output intersection point �Case 3 : No output �Case 4 : Output intersection point & vi+1} 39

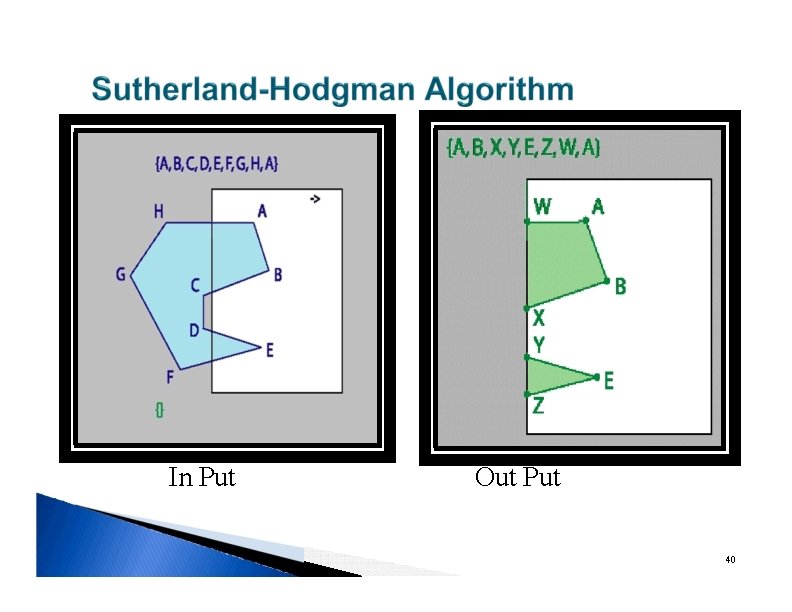
In Put Out Put 40