UNIT II 2 D TRANSFORMATIONS Objectives n Basic

UNIT II 2 D TRANSFORMATIONS

Objectives n Basic 2 D Transformations (rigid-body transformations): q q q n n Translation Rotation Scaling Homogenenous Representations and Coordinates 2 D Composite Transformations Computer Graphics Rathi, AP(SG) M. 2

Objectives (cont. ) n Other Transformations: q q n n Reflection Shearing Raster Methods for Transformations and Open. GL Transformations between 2 D Coordinate Systems and Open. GL Computer Graphics Rathi, AP(SG) M. 3

Geometric Transformations n Sometimes also called modeling transformations q q n Geometric transformations: Changing an object’s position (translation), orientation (rotation) or size (scaling) Modeling transformations: Constructing a scene or hierarchical description of a complex object Others transformations: reflection and shearing operations Computer Graphics M. Rathi, AP(SG) 4

Basic 2 D Geometric Transformations n 2 D Translation P’ T q q q x’ = x + tx , y’ = y + ty P P’=P+T Translation moves the object without deformation Computer Graphics (rigid-body transformation) M. Rathi, AP(SG) 5

Basic 2 D Geometric Transformations (cont. ) n 2 D Translation q q To move a line segment, apply the transformation equation to each of the two line endpoints and redraw the line between new endpoints To move a polygon, apply the transformation equation to coordinates of each vertex and regenerate the polygon using the new set of vertex coordinates Computer Graphics M. Rathi, AP(SG) 6

Basic 2 D Geometric Transformations (cont. ) n 2 D Rotation q q q Rotation axis Rotation angle rotation point or pivot point (xr, yr) θ yr xr Computer Graphics M. Rathi, AP(SG) 7

Basic 2 D Geometric Transformations (cont. ) n 2 D Rotation q q q If θ is positive counterclockwise rotation If θ is negative clockwise rotation Remember: n n cos(a + b) = cos a cos b - sin a sin b cos(a - b) = cos a sin b + sin a cos b Computer Graphics M. Rathi, AP(SG) 8

Basic 2 D Geometric Transformations (cont. ) n 2 D Rotation At first, suppose the pivot point is at the origin x’=r cos(θ+Φ) = r cos θ cos Φ - r sin θ sin Φ y’=r sin(θ+Φ) = r cos θ sin Φ + r sin θ cos Φ x = r cos Φ, y = r sin Φ x’=x cos θ - y sin θ y’=x sin θ + y cos θ q q (x’, y’) r θ Φ r (x, y) Computer Graphics M. Rathi, AP(SG) 9

Basic 2 D Geometric Transformations n 2 D Rotation P’=R·P q (x’, y’) r θ Φ r (x, y) Computer Graphics M. Rathi, AP(SG) 10

Basic 2 D Geometric Transformations (cont. ) n 2 D Rotation q q Rotation of a point about any specified position (xr, yr) x’=xr+(x - xr) cos θ – (y - yr) sin θ y’=yr+(x - xr) sin θ + (y - yr) cos θ Rotations also move objects without deformation A line is rotated by applying the rotation formula to each of the endpoints and redrawing the line between the new end points A polygon is rotated by applying the rotation formula to each of the vertices and redrawing the polygon using new vertex coordinates Computer Graphics M. Rathi, AP(SG) 11

Basic 2 D Geometric Transformations (cont. ) n 2 D Scaling q q Scaling is used to alter the size of an object Simple 2 D scaling is performed by multiplying object positions (x, y) by scaling factors sx and sy x’ = x · sx y’ = y · sx or P’ = S·P Computer Graphics M. Rathi, AP(SG) 12

Basic 2 D Geometric Transformations (cont. ) n 2 D Scaling q Any positive value can be used as scaling factor n n n x’ Values less than 1 reduce the size of the object Values greater than 1 enlarge the object If scaling factor is 1 then the object stays unchanged If sx = sy , we call it uniform scaling If scaling factor <1, then the object moves closer to the origin and If scaling factor >1, then the object moves farther from the origin x Computer Graphics M. Rathi, AP(SG) 13

Basic 2 D Geometric Transformations (cont. ) n Computer Graphics M. Rathi, AP(SG) 14

Basic 2 D Geometric Transformations (cont. ) n 2 D Scaling q q We can control the location of the scaled object by choosing a position called the fixed point (xf, yf) x’ – xf = (x – xf) sx y’ – yf = (y – yf) sy x’=x · sx + xf (1 – sx) y’=y · sy + yf (1 – sy) Polygons are scaled by applying the above formula to each vertex, then regenerating the polygon using the transformed vertices Computer Graphics M. Rathi, AP(SG) 15

Matrix Representations and Homogeneous Coordinates n Many graphics applications involve sequences of geometric transformations q q n Animations Design and picture construction applications We will now consider matrix representations of these operations q Sequences of transformations can be efficiently processed using matrices Computer Graphics M. Rathi, AP(SG) 16

Matrix Representations and Homogeneous Coordinates (cont. ) n P’ = M 1 · P + M 2 q q q P and P’ are column vectors M 1 is a 2 by 2 array containing multiplicative factors M 2 is a 2 element column matrix containing translational terms For translation M 1 is the identity matrix For rotation or scaling, M 2 contains the translational terms associated with the pivot point or scaling fixed point Computer Graphics M. Rathi, AP(SG) 17

Matrix Representations and Homogeneous Coordinates (cont. ) n n To produce a sequence of operations, such as scaling followed by rotation then translation, we could calculate the transformed coordinates one step at a time A more efficient approach is to combine transformations, without calculating intermediate coordinate values Computer Graphics M. Rathi, AP(SG) 18

Matrix Representations and Homogeneous Coordinates (cont. ) n Multiplicative and translational terms for a 2 D geometric transformation can be combined into a single matrix if we expand the representations to 3 by 3 matrices q We can use third column for translation terms, and all transformation equations can be expressed as matrix multiplications Computer Graphics M. Rathi, AP(SG) 19

Matrix Representations and Homogeneous Coordinates (cont. ) n n Expand each 2 D coordinate (x, y) to three element representation (xh, yh, h) called homogeneous coordinates h is the homogeneous parameter such that x = xh/h, y = yh/h, infinite homogeneous representations for a point A convenient choice is to choose h = 1 Computer Graphics M. Rathi, AP(SG) 20

Matrix Representations and Homogeneous Coordinates (cont. ) n 2 D Translation Matrix or, P’ = T(tx, ty)·P Computer Graphics M. Rathi, AP(SG) 21

Matrix Representations and Homogeneous Coordinates (cont. ) n 2 D Rotation Matrix or, P’ = R(θ)·P Computer Graphics M. Rathi, AP(SG) 22

Matrix Representations and Homogeneous Coordinates (cont. ) n 2 D Scaling Matrix or, P’ = S(sx, sy)·P Computer Graphics M. Rathi, AP(SG) 23

Inverse Transformations n 2 D Inverse Translation Matrix n By the way: Computer Graphics M. Rathi, AP(SG) 24

Inverse Transformations (cont. ) n 2 D Inverse Rotation Matrix n And also: Computer Graphics M. Rathi, AP(SG) 25

Inverse Transformations (cont. ) n 2 D Inverse Rotation Matrix: q q q If θ is negative clockwise In Only sine function is affected Therefore we can say Is that true? Proof: It’s up to you Computer Graphics M. Rathi, AP(SG) 26

Inverse Transformations (cont. ) n 2 D Inverse Scaling Matrix n Of course: Computer Graphics M. Rathi, AP(SG) 27

2 D Composite Transformations n n We can setup a sequence of transformations as a composite transformation matrix by calculating the product of the individual transformations P’=M 2·M 1·P =M·P Computer Graphics M. Rathi, AP(SG) 28

2 D Composite Transformations (cont. ) n Composite 2 D Translations q If two successive translation are applied to a point P, then the final transformed location P' is calculated as Computer Graphics M. Rathi, AP(SG) 29

2 D Composite Transformations (cont. ) n Composite 2 D Rotations Computer Graphics M. Rathi, AP(SG) 30

2 D Composite Transformations (cont. ) n Composite 2 D Scaling Computer Graphics M. Rathi, AP(SG) 31

2 D Composite Transformations (cont. ) Don’t forget: Successive translations are additive Successive scalings are multiplicative n n n q q For example: If we triple the size of an object twice, the final size is nine (9) times the original 9 times? Why? Proof: Again up to you Computer Graphics Rathi, AP(SG) M. 32

General Pivot Point Rotation n Steps: 1. 2. 3. Translate the object so that the pivot point is moved to the coordinate origin. Rotate the object about the origin. Translate the object so that the pivot point is returned to its original position. Computer Graphics Rathi, AP(SG) M. 33
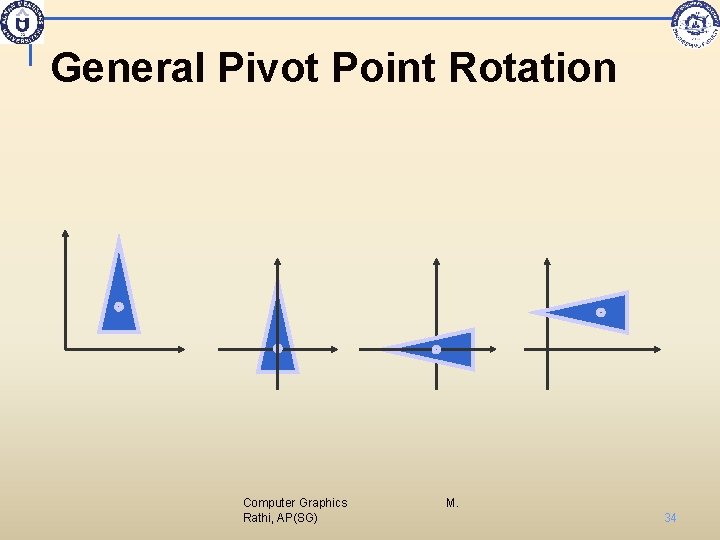
General Pivot Point Rotation Computer Graphics Rathi, AP(SG) M. 34

2 D Composite Transformations (cont. ) n General 2 D Pivot-Point Rotation Computer Graphics M. Rathi, AP(SG) 35

General Fixed Point Scaling n Steps: 1. 2. 3. Translate the object so that the fixed point coincides with the coordinate origin. Scale the object about the origin. Translate the object so that the pivot point is returned to its original position. Computer Graphics Rathi, AP(SG) M. 36

General Fixed Point Scaling (cont. ) l(xr, yr) Computer Graphics Rathi, AP(SG) M. 37

General Fixed Point Scaling (cont. ) • General 2 D Fixed-Point Scaling: Computer Graphics Rathi, AP(SG) M. 38

2 D Composite Transformations (cont. ) n General 2 D scaling directions: q q q Above: scaling parameters were along x and y directions What about arbitrary directions? Answer: See next slides Computer Graphics M. Rathi, AP(SG) 39

General 2 D Scaling Directions Scaling parameters s 1 and s 2 along Computer Graphicsorthogonal directions defined by the 40 angular displacement θ. M. Rathi, AP(SG)

General 2 D Scaling Directions (cont. ) Computer Graphics M. Rathi, AP(SG) 41

2 D Composite Transformations (cont. ) n Matrix Concatenation Properties: q Matrix multiplication is associative ! n n q M 3· M 2· M 1= (M 3· M 2 ) · M 1 = M 3· ( M 2 · M 1 ) A composite matrix can be created by multiplicating leftto-right (premultiplication) or right-to-left (postmultiplication) Matrix multiplication is not commutative ! n M 2 · M 1 ≠ M 1 · M 2 Computer Graphics M. Rathi, AP(SG) 42

2 D Composite Transformations (cont. ) n Matrix Concatenation Properties: n But: q q q n q q Two successive rotations Two successive translations Two successive scalings are commutative! Why? Proof: You got it: Up to you Computer Graphics M. Rathi, AP(SG) 43

Reversing the order in which a sequence of transformations is performed may affect the transformed position of an object. In (a), an object is first translated in the x direction, then rotated counterclockwise through an angle of 45°. In (b), the object is first rotated 45° counterclockwise, then translated in the x direction Computer Graphics M. Rathi, AP(SG) 44

Other 2 D Transformations n Reflection q Transformation that produces a mirror image of an object Computer Graphics M. Rathi, AP(SG) 45
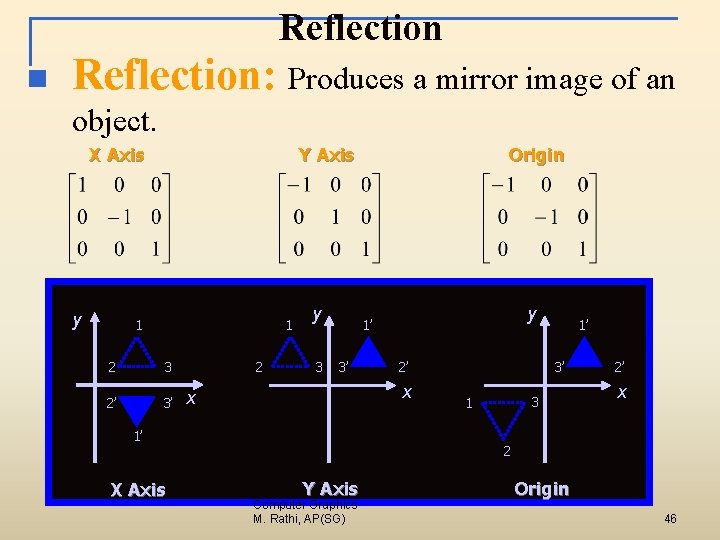
Reflection n Reflection: Produces a mirror image of an object. X Axis y Y Axis 1 1 2 3 2’ 3’ 2 y 3 y 1’ 3’ 2’ x x 1’ X Axis Origin 1’ 3’ 3 1 2’ x 2 Y Axis Computer Graphics M. Rathi, AP(SG) Origin 46

Other 2 D Transformations (cont. ) n Reflection q Image is generated relative to an axis of reflection by rotating the object 180° about the reflection axis Computer Graphics M. Rathi, AP(SG) 47
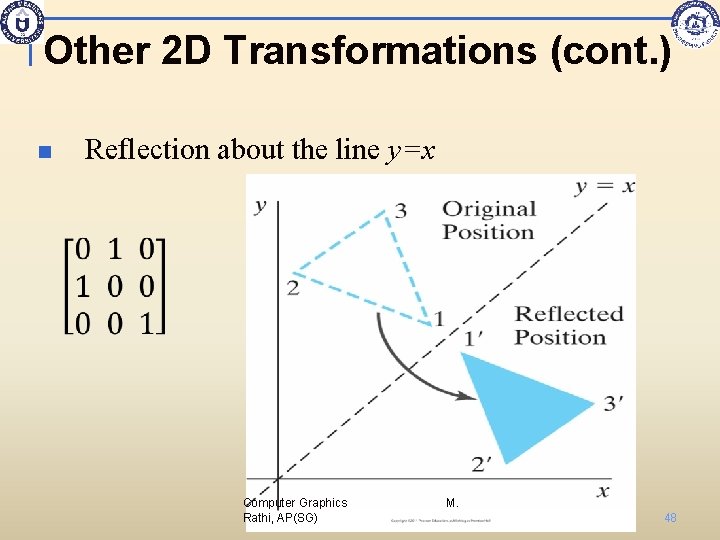
Other 2 D Transformations (cont. ) n Reflection about the line y=x Computer Graphics Rathi, AP(SG) M. 48

Other 2 D Transformations (cont. ) n Reflection about the line y=-x Computer Graphics Rathi, AP(SG) M. 49

Other 2 D Transformations (cont. ) n • • • Shear A Transformation that slants the shape of an object is called the shear transformation. Two common shearing transformations are used. 1. shifts x coordinate values 2. shift y coordinate values. However in both the cases only one coordinate (x or y) changes its coordinates and other preserves its values. Computer Graphics M. Rathi, AP(SG) 50
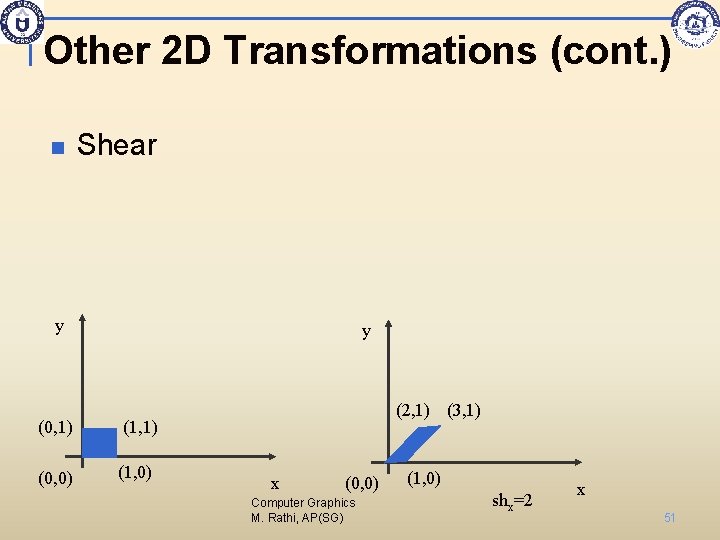
Other 2 D Transformations (cont. ) n Shear y (0, 1) (0, 0) y (2, 1) (3, 1) (1, 0) x (0, 0) Computer Graphics M. Rathi, AP(SG) (1, 0) shx=2 x 51

Other 2 D Transformations (cont. ) n Shear q An x-direction shear relative to the x axis q An y-direction shear relative to the y axis Computer Graphics M. Rathi, AP(SG) 52

Other 2 D Transformations (cont. ) n Shear q x-direction shear relative to other reference lines Computer Graphics M. Rathi, AP(SG) 53

Example A unit square (a) is transformed to a shifted parallelogram (b) with shx = 0. 5 and yref = − 1 in the shear matrix from Slide 56 Computer Graphics M. Rathi, AP(SG) 54

Other 2 D Transformations (cont. ) n Shear q y-direction shear relative to the line x = xref Computer Graphics M. Rathi, AP(SG) 55
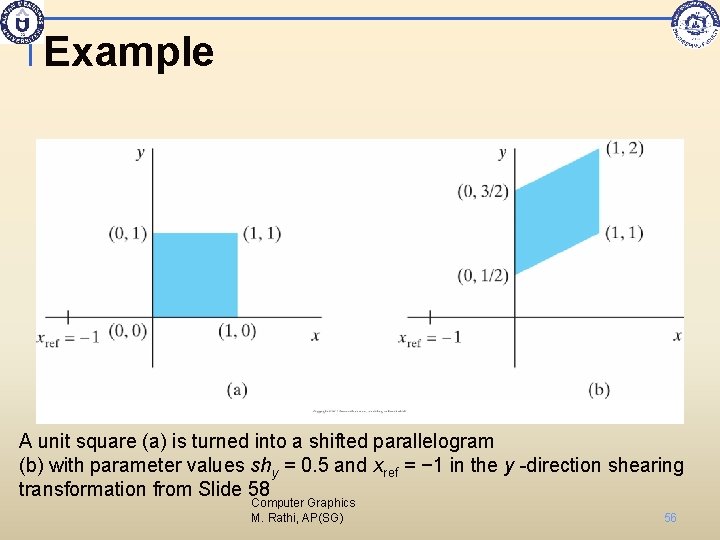
Example A unit square (a) is turned into a shifted parallelogram (b) with parameter values shy = 0. 5 and xref = − 1 in the y -direction shearing transformation from Slide 58 Computer Graphics M. Rathi, AP(SG) 56
- Slides: 56