Unit ConversionsTake II We use the FactorLabel method

Unit Conversions-Take II We use the Factor-Label method to convert from one unit to another. Key Idea: -Use “conversion factors” to convert between units. PAY ATTENTION TO UNITS so that they cancel. Units are your friends!!! They prevent mistakes

1 km = 1000 m (This is called an Equivalence Statement or Definition) Any equivalence statement can be made into two (conversion factors) 1000 m = 1 km Note: both of these = 1 1 km 1000 m Which one to use? Depends on which direction you are trying to go.

For example: Convert 25 km to meters Use the conversion factor that allows units to cancel. Which one? 1000 m or 1 km 1000 m 25 km x 1000 m = 25000 m (or 2. 5 x 104 m) 1 km given conversion factor

Step-By-Step Method to Solving Problems. Example: How many centimeters are there in 5. 54 inches? – Step 1: Find how many centimeters are equal to one inch (Equivalence Statement). 1 inch = 2. 54 cm or 2. 54 cm = 1 inch

Step 2: Turn the statement into a “conversion factor” 1 inch 2. 54 cm = 1 or 2. 54 cm = 1 1 inch Step 3: Multiply the given by the conversion factor which will allow the unit to cancel out. 5. 54 inch X 2. 54 cm = 14. 1 cm 1 inch given conversion factor

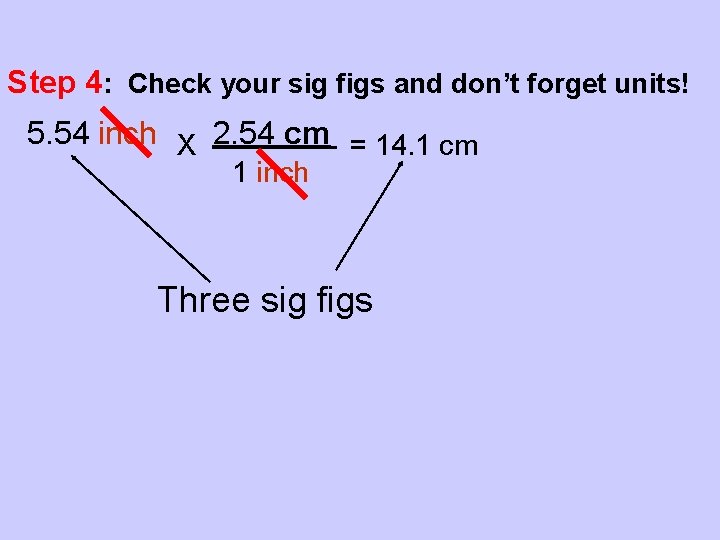
Step 4: Check your sig figs and don’t forget units! 5. 54 inch X 2. 54 cm = 14. 1 cm 1 inch Three sig figs

Ex #2. How many kilometers is the 26. 2 mile marathon? Definition: 1 mi = 1. 6093 km or 1 km =. 62137 mi 26. 2 mi x 1. 6093 km = 42. 2 km 1 mi given conversion factor

You can do more than one conversion at a time. Example: How many inches in 4. 2 meters? Definitions: 1 meter = 100 cm 1 inch = 2. 54 cm Set up: 4. 2 meters X 100 cm X 1 meter given conversion factor 1 inch = ? ? ? 2. 54 cm conversion factor

Top and Bottom Conversions: Mr Clauson’s Durango gets 7. 2 km/L of gas. How many miles per gallon is that? Logic: Need to go from km mi on top, and from L to gal on the bottom. 1 mi = 1. 6093 km; 1 gal = 3. 7854 L 7. 2 km x 1 mi x 3. 7854 L = 1 L 1. 6093 km 1 gal Are the Sig Figs right? NO!! 17 mpg

Another Top and Bottom example: This year in physics, the fastest baseball throw was 39. 8 m/sec. What is the speed in miles/hour? • Logic: Need to go from m mi on top, and from sec to hr on the bottom. 1 m = 3. 28 ft; 1 mi = 5280 ft; 1 hr = 60 min; 1 min = 60 sec

Doing Area Conversions Use the conversion factors, but square them!! Example: How many square feet in 3. 3 square yards? The linear conversion factor 1 yard = 3 feet Has to be squared! 3. 3 yd 2 X 3 ft = 3. 3 yd 2 x 3 ft 1 yd 2 = Answer = 29. 7 sq ft = 3. 0 x 101 sq ft (sig figs!)

Doing Volume Conversions Use the conversion factors, but cube them!! Example: How many cubic meters in 357 cm 3? The linear conversion factor 1 m = 100 cm Has to be cubed! 3. 57 cm 3 X 1 m 100 cm X 100 cm 1 m = 3. 57 cm 3 x 100 cm Answer = 3. 57 x 10 -6 cubic meters 1 m 100 cm 3

Homework • Paddy’s Pool Procedure (Your individual best!) • Conversion WS #3

Learning Check A Nalgene water bottle holds 1000 cm 3 of dihydrogen monoxide (H 2 O). How many cubic decimeters is that?

Solution 1000 cm 3 ( ) 1 dm 10 cm 3 = 1 dm 3 So, a dm 3 is the same as a Liter ! A cm 3 is the same as a milliliter.