Unit Conversion Recall Math 10 you did unit

Unit Conversion

Recall • Math 10, you did unit conversions from metric to imperial. – If you followed the unit cancellation method, you are already ahead. If not, we will work on it. • You are driving from Vancouver to Toronto • You travel at 100 km/h. It took you 55 hours to get to Toronto • How far is it from Vancouver to Toronto?

Unit Conversions - 1 • Lets say you can buy 5 carrots for $1. 60. – Well this means 5 carrots = $1. 60 – We can represent it as a ratio as well since its • 5 carrots : $1. 60 • But how else can we represent it? – AS A FRACTION! • It can be represented as 5 carrots / $1. 60 • Or $1. 60/ 5 carrots • This means the top and the bottom part are equivalent! • Because they are equal, they are equal to 1!

Unit Conversion - 2 • We use conversions everywhere! • We use it for time! – 60 seconds = 1 minute – 60 minutes = 1 hour – 24 hours = 1 day – 7 days = 1 week – 52 weeks = 1 year – 365 days = 1 year – 10 years = 1 decade • We can put all of these into fractions!

Unit Conversion - 3 • Strategies to solving questions – Your conversion factors can be put into fractions • Ie. 60 min/1 hour or 1 hour/60 min – Whatever units you want to cancel, they can only cancel if you have 1 in the numerator and one in the denominator • So flip your conversion factors according to cancellation! – Multiplying fractions means multiplying across • Numerators with numerators • Denominators with denominators – Values without any denominator will have a denominator of 1! – The unit you want to solve should be the only unit left after you cancel everything out!

Sample - 1 • 5 A’s = 9 B’s • How many A’s will you get for 81 B’S? • This is basically proportional reasoning, but with multiple steps • 5 A = 9 B • x. A = 81 B

Example 1. • How many days are in 35679 seconds?

Example 2 • How many millimeters are in 1. 679 miles?

Example 3 • If a car can go 150 km in 1 hour. How far can it go in 24 hours?

Unit Conversion - 4 • You cancel things in the denominator too! • As long as you follow the strategies that the units you want are the only units remaining after cancellation

Example - 4 • Gasoline currently cost around $1. 31/litre. What is the price per gallon?

Example - 5 • The density of liquid methanol is 0. 678 g/m. L. What is the density if the units are in lb/L?

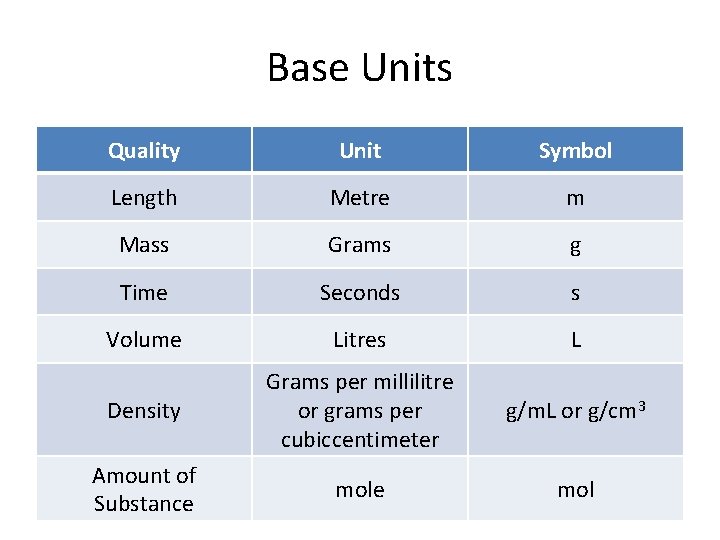
SI Units • SI = Systeme International in French • Or the International System in English • The SI units has base units – Base units are the main units we use to represent each quality of something • Pressure, temperature, mass, volume etc

Base Units Quality Unit Symbol Length Metre m Mass Grams g Time Seconds s Volume Litres L Density Grams per millilitre or grams per cubiccentimeter g/m. L or g/cm 3 Amount of Substance mol

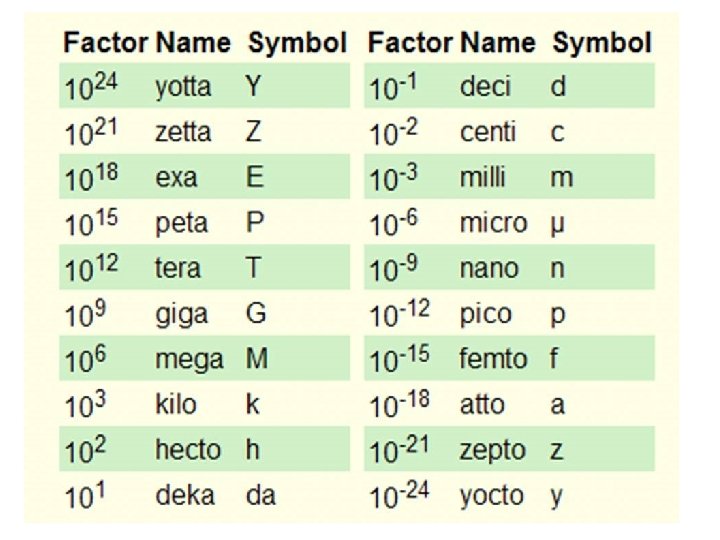
How to read the prefixes • 103 or 1000 means kilo – So 1000 grams = 1 kilogram • 10 -3 or 0. 001 means milli – So 0. 001 L is 1 m. L • You have to think that each prefix means the BASE unit and the name means the unit it is turning into! • There is MEGA which means 1 million • Micro which means 1 millionth

How to read the prefixes • But if you want to represent 50 m. L into L, you have two ways – 1. 0. 050 L – 2. 50 x 10 -3 L (multiply 50 by its prefix multiple) • Both ways work and give you 0. 050 L

But what do you need to know? • • You need to know Milli, Centi, Kilo, and Micro You also need to know 1 m. L = 1 cm 3 – So a box that means 1 cm by 1 cm will take up 1 m. L of space • 1 ton = 1000 kg

So what does this all mean? • We can do unit conversions and turn these SI units into conversion factors • 0. 001 L = 1 m. L can be turned into a fraction • 1000 m = 1 km can be turned into a fraction

Example - 6 • • • 10 kilograms to grams 5 ms to s 5. 3 x 10 -2 m to cm 30 tonnes to kg 5 Mg/m. L to kg/L

Practice – 1 Unit Conversion and SI Units • Page 19 #11 -14 • Page 21 - #17 • Page 22 - #18 -19

Derived Quantities • Derived quantities are numbers made by combining two or more other values • Derived unit is a unit which is made by combining two or more other units • Density = g/m. L • Area = m 2 • Concentration = mol/L • Newton = kg*m/s 2

Density • • It is the mass (g) per a unit volume (m. L or cm 3) Density = mass/volume d = m/v Water has a density of 1 g/m. L at 4°C

Note! When you get 5 g/3 m. L We can rearrange and get 5/3 * g/m. L We never want a denominator other than 1 with density or any derived unit. • So we must divided 5 by 3 • 1. 6666 g/m. L • •

Example - 7 • Find the density of an object with the mass of 600 g and a volume of 1. 2 L?

Example - 8 • A piece of gold has a mass of 29. 2 kg and a volume of 2. 5 L. What is its density in g/m. L?

Example - 9 • Bromine, a liquid has a density of 1200 g/L and has a mass of 123 g, what volume will the bromine take up in m. L?

Practice – 2 Derived Units • Page 26 - #31 -41 (pick 5)