Unit 8 Trigonometry Part 2 By Ginamarie Ivers

Unit 8: Trigonometry (Part 2) By Ginamarie Ivers

Parts of a Periodic Function Periodic functions have y-vales that repeat at regular intervals Cycle: one complete pattern Period: the horizontal length of one cycle Amplitude: one half of the distance between the maximum and minimum vales of the function Asymptote: a line that a curve approaches but does not meet

Sine Graph Parent Function y=sinq Domain All real numbers Range {y| -1 ≤ y ≤ 1} Amplitude 1 Period 360º X-intercepts (0, 0) (½ • 360/b, 0) (360/b, 0)

Cosine Graph Parent Function y=cosq Domain All real numbers Range {y| -1 ≤ y ≤ 1} Amplitude 1 Period 360º X-intercepts (¼ • 360/b, 0) (¾ • 360/b, 0)

Tangent Graph Parent Function y=tanq Domain {q|q≠ 90+180 n} Range All real numbers Amplitude undefined Period 180º X-intercepts (0, 0) (½ • 360/b, 0) (360/b, 0)

Sine. Transformations and Cosine Tangent Basic forms y=asinbq y=acosbq amplitude= |a| period= 360/|b| Basic form y=atanbq period= 180/|b| asymptote= 180/2|b asymptotes are only the odd multiples there is no amplitude

Translations Phase shift (h): horizontal translation equations: y=asinb(q-h) y=acosb(q-h) y=atanb(q-h) phase shift to right: h<0 phase shift to left: h>0 Vertical Shift (k) equations: y=asin(bq)+k upwards shift: k>0 downwards shift : k<0 midline: new horizontal axis about which the graph oscillates y=k

Frequency: number of cycles in a given unit of time; how many cycles are within 2π In applications, it is the reciprocal of the period of the function
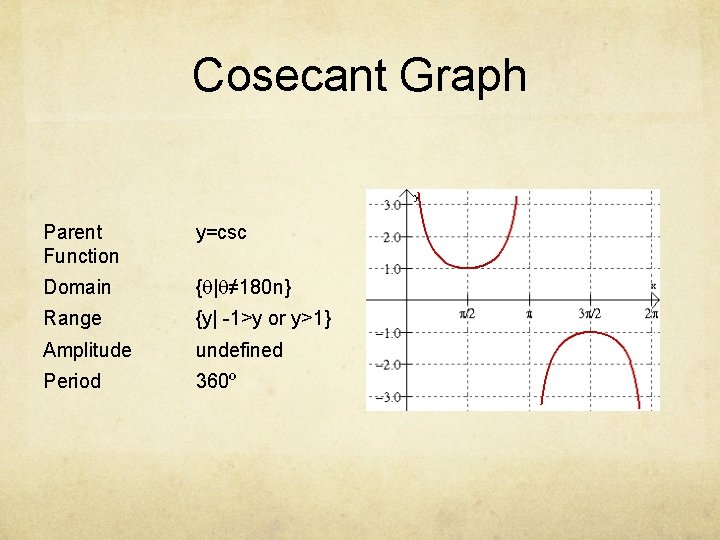
Cosecant Graph Parent Function y=csc Domain {q|q≠ 180 n} Range {y| -1>y or y>1} Amplitude undefined Period 360º

Secant Graph Parent Function y=sec Domain {q|q≠ 90+180 n} Range {y| -1>y or y>1} Amplitude undefined Period 360º
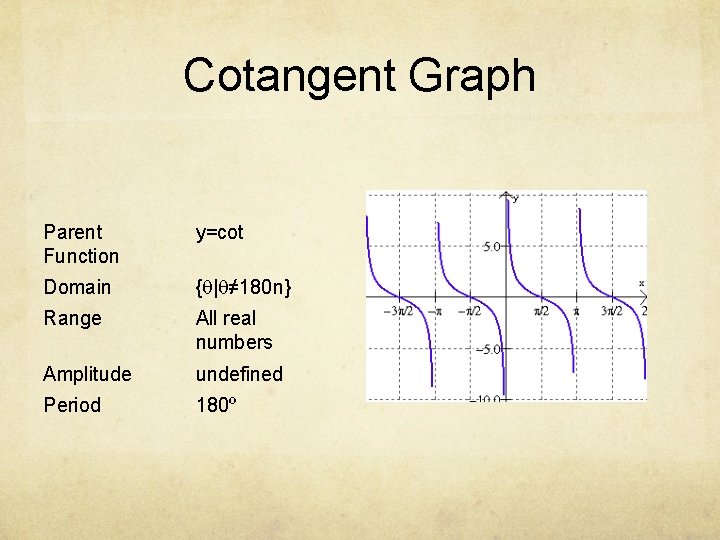
Cotangent Graph Parent Function y=cot Domain {q|q≠ 180 n} Range All real numbers Amplitude undefined Period 180º

Inverse Trigonometric Functions Inverse function: all values of x and y are switched When this is done, domains must be restricted, or else it it not a function Arccosine y=arccos(x) or y=cos-1 x Domain: -1 ≤ x ≤ 1 Range: 0 ≤ y ≤ π Arcsine y=arcsin(x) or y=sin-1 x Domain: -1 ≤ x ≤ 1 Range: -π/2 ≤ y ≤ π/2 Arctangent y=arctan(x) or y=tan-1 x Domain: all real numbers Range: -π/2 ≤ y ≤ π/2
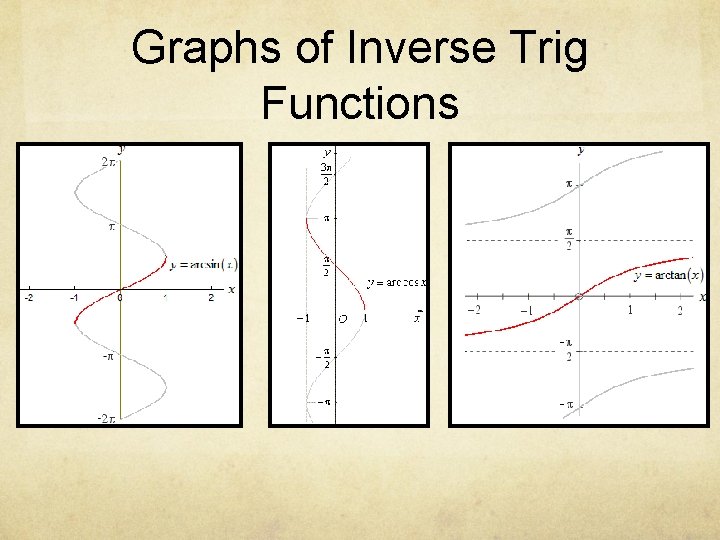
Graphs of Inverse Trig Functions

Practice Problem #1 Relative to the graph of y=3 sinx, what is the shift of the graph of y=3 sin(x+π/3)? 1) π/3 right 2) π/3 left 3) π/3 up 4) π/3 down Answer: 2) π/3 left Mistakes and Things to Remember: • y=3 sinx has no phase or vertical shifts • When there is a number inside the parentheses following the x (h value), as in the equation, it is a phase shift to the left or right. • y=asinb(q-h) • Phase shifts to the left are +h, and to the right are –h • If using calculator to graph, remember
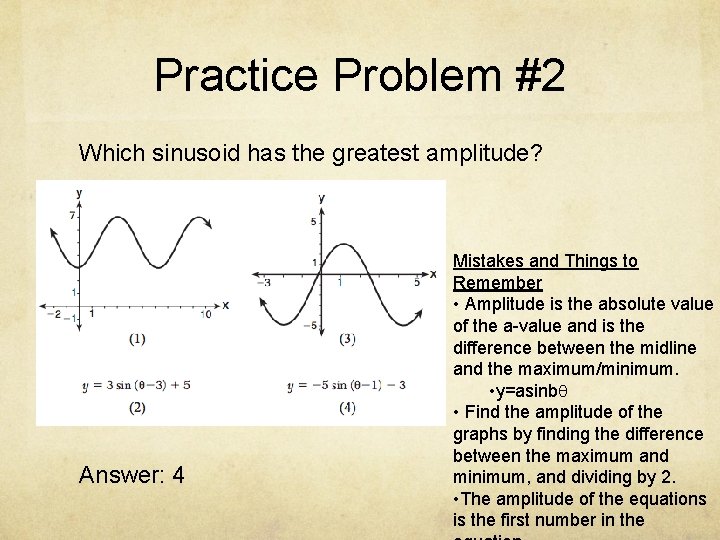
Practice Problem #2 Which sinusoid has the greatest amplitude? Answer: 4 Mistakes and Things to Remember • Amplitude is the absolute value of the a-value and is the difference between the midline and the maximum/minimum. • y=asinbq • Find the amplitude of the graphs by finding the difference between the maximum and minimum, and dividing by 2. • The amplitude of the equations is the first number in the

Practice Problem #3 The graph below represents the height above the ground, h, in inches, of a point on a triathlete's bike wheel during a Mistakes and Things training ride in terms of time, t, in seconds. to Remember • Remember what one cycle of a cosine graph looks like to identify the period • Read the question to know that the x-axis is the height of the wheel relative to the ground Identify the period of the graph and describe what the period • With that represents in this situation. information, you can determine Answer: the period of the graph represents the amount of that one cycle is a rotation time it takes for the wheel to complete one rotation; because it period=2/3

Practice Problem #4 As x increases from 0 to π/2, the graph of the equation y=2 tanx will 1) Increase from 0 to 2 2) Decrease from 0 to -2 3) Increase without limit 4) Decrease without limit Answer: 3 Mistakes and Things to Remember: • The amplitude of a tangent graph does not matter. • y=atanbq • Since there is no b value, the period is 180 (π) and the asymptote is 90 (π/2) • Remember to convert to radians • Because the asymptote is 90 (π/2),
- Slides: 17