Unit 8 Triangles This unit continues with triangles

Unit 8 –Triangles • This unit continues with triangles. • It defines midsegments, bisectors, altitudes, medians, centroids, points of concurrency, incenters, inscribed circles, circumscribed circles, midpoints and perpendicular bisectors. • It also proves triangles are congruent by SSS, SAS, ASA, AAS, HL, and CPCTC.

Standards • • • • • SPI’s taught in Unit 8: SPI 3108. 1. 1 Give precise mathematical descriptions or definitions of geometric shapes in the plane and space. SPI 3108. 4. 11 Use basic theorems about similar and congruent triangles to solve problems. SPI 3108. 4. 12 Solve problems involving congruence, similarity, proportional reasoning and/or scale factor of two similar figures or solids. CLE (Course Level Expectations) found in Unit 8: CLE 3108. 1. 2 Apply and adapt a variety of appropriate strategies to problem solving, including testing cases, estimation, and then checking induced errors and the reasonableness of the solution. CLE 3108. 1. 4 Move flexibly between multiple representations (contextual, physical written, verbal, iconic/pictorial, graphical, tabular, and symbolic), to solve problems, to model mathematical ideas, and to communicate solution strategies. CLE 3108. 1. 5 Recognize and use mathematical ideas and processes that arise in different settings, with an emphasis on formulating a problem in mathematical terms, interpreting the solutions, mathematical ideas, and communication of solution strategies. CLE 3108. 1. 7 Use technologies appropriately to develop understanding of abstract mathematical ideas, to facilitate problem solving, and to produce accurate and reliable models. CLE 3108. 4. 8 Establish processes for determining congruence and similarity of figures, especially as related to scale factor, contextual applications, and transformations. CFU (Checks for Understanding) applied to Unit 8: 3108. 1. 5 Use technology, hands-on activities, and manipulatives to develop the language and the concepts of geometry, including specialized vocabulary (e. g. graphing calculators, interactive geometry software such as Geometer’s Sketchpad and Cabri, algebra tiles, pattern blocks, tessellation tiles, MIRAs, mirrors, spinners, geoboards, conic section models, volume demonstration kits, Polyhedrons, measurement tools, compasses, Penta. Blocks, pentominoes, cubes, tangrams). 3108. 1. 7 Recognize the capabilities and the limitations of calculators and computers in solving problems. 3108. 4. 35 Prove that two triangles are congruent by applying the SSS, SAS, ASA, AAS, and HL congruence statements. 3108. 4. 36 Use several methods, including AA, SSS, and SAS, to prove that two triangles are similar. 3108. 4. 38 Use the principle that corresponding parts of congruent triangles are congruent to solve problems. 3108. 4. 41 Use inscribed and circumscribed polygons to solve problems concerning segment length and angle measures.

A basic review before we move on… • Triangle Sum theorem: The sum of the measure of the angles of a triangle is…. – m of angle A plus angle B plus angle C = 180 • Triangles classified by sides: – Equilateral (all sides equal) – Isosceles (at least 2 sides equal) – Scalene (no sides equal) • Triangles classified by angles: – – Equiangular (all angles equal) Acute (all angles acute) (less than 90 degrees) Right (one right angle) (equal to 90 degrees) Obtuse (one obtuse angle) (greater than 90 degrees)

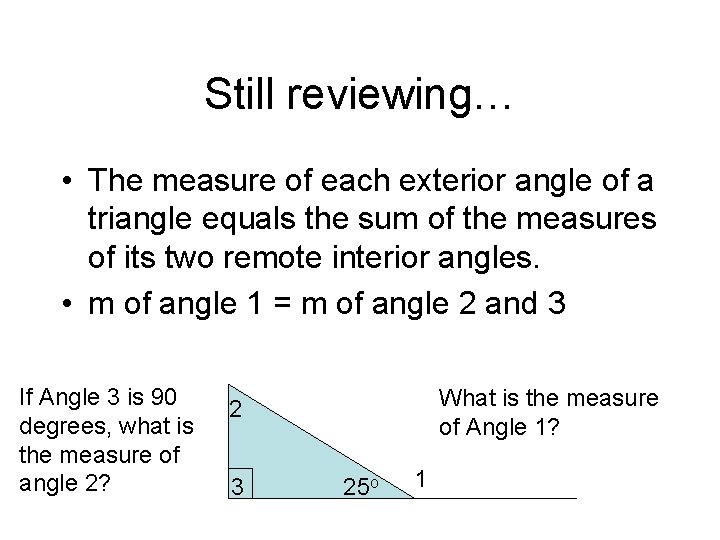
Still reviewing… • The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles. • m of angle 1 = m of angle 2 and 3 If Angle 3 is 90 degrees, what is the measure of angle 2? What is the measure of Angle 1? 2 3 25 o 1

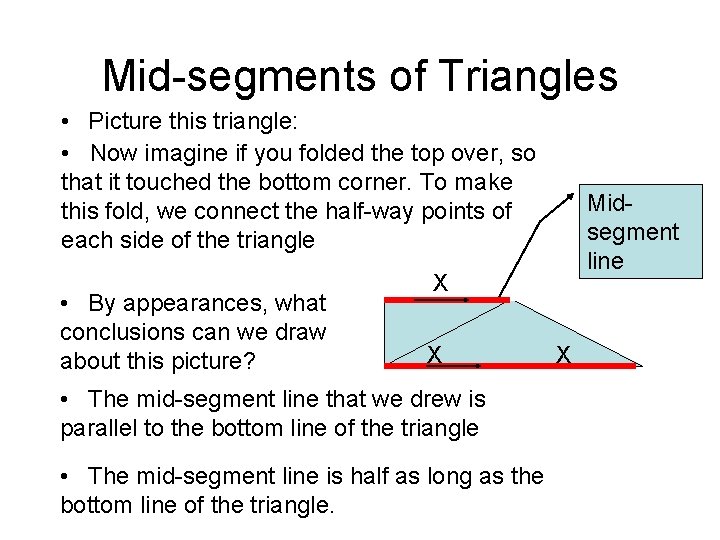
Mid-segments of Triangles • Picture this triangle: • Now imagine if you folded the top over, so that it touched the bottom corner. To make this fold, we connect the half-way points of each side of the triangle • By appearances, what conclusions can we draw about this picture? Midsegment line X X • The mid-segment line that we drew is parallel to the bottom line of the triangle • The mid-segment line is half as long as the bottom line of the triangle. X

Triangle Mid-segment Theorem • Therefore we can create a theorem to capture these ideas: • If a segment joins the midpoints of two sides of a triangle, then the segment is parallel to the third side, and is half its length • Converse thinking comes in handy here as well -> if it’s not connecting two midpoints, then its not parallel, and it’s not half as long… • …and, if a segment connects a midpoint, it’s parallel to a side… • Therefore, three segments connecting midpoints would create three parallel sides, and you would have a triangle which is half as big…whew…

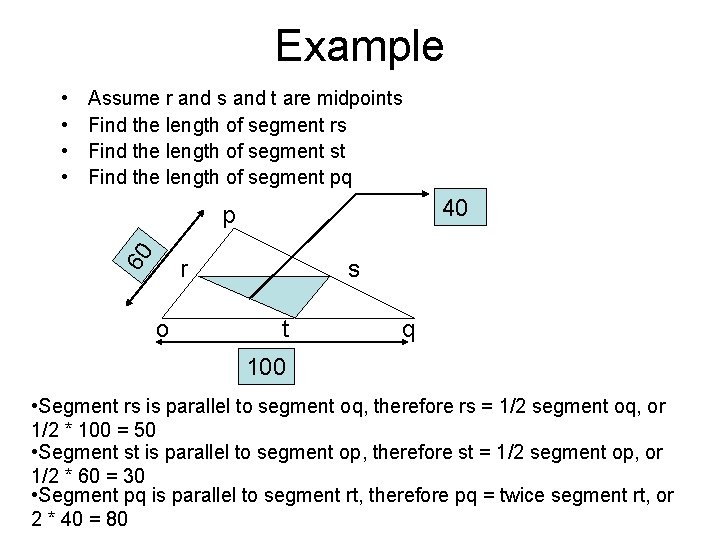
Example • • Assume r and s and t are midpoints Find the length of segment rs Find the length of segment st Find the length of segment pq 40 60 p r o s t q 100 • Segment rs is parallel to segment oq, therefore rs = 1/2 segment oq, or 1/2 * 100 = 50 • Segment st is parallel to segment op, therefore st = 1/2 segment op, or 1/2 * 60 = 30 • Segment pq is parallel to segment rt, therefore pq = twice segment rt, or 2 * 40 = 80

Assignment • Page 288 -289 7 -26 • Worksheet 5 -1

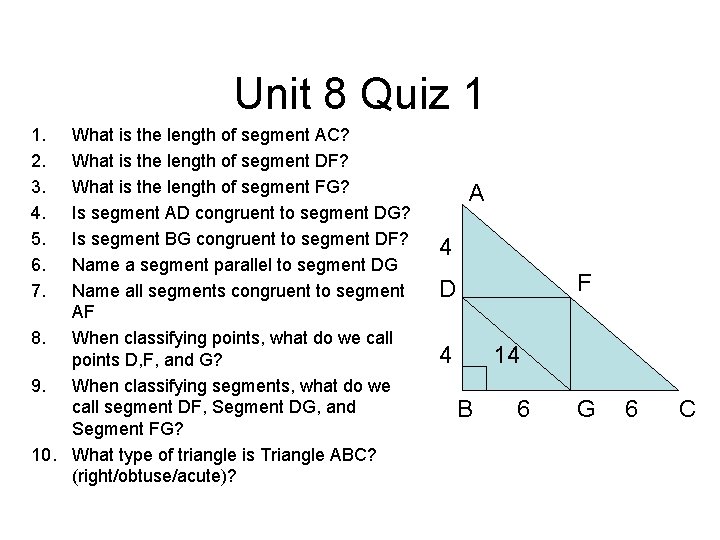
Unit 8 Quiz 1 1. 2. 3. 4. 5. 6. 7. What is the length of segment AC? What is the length of segment DF? What is the length of segment FG? Is segment AD congruent to segment DG? Is segment BG congruent to segment DF? Name a segment parallel to segment DG Name all segments congruent to segment AF 8. When classifying points, what do we call points D, F, and G? 9. When classifying segments, what do we call segment DF, Segment DG, and Segment FG? 10. What type of triangle is Triangle ABC? (right/obtuse/acute)? A 4 F D 4 14 B 6 G 6 C

Bisectors in Triangles • This is really a review, but hey… • Theorem - If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment (that’s why it’s called a bisector, right? ) • Converse: If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment

Angle Bisector Theorem • Theorem - If a point is on the bisector of an angle, then the point is equidistant from the sides of the angle • Converse - If a point in the interior of an angle is equidistant from the sides of the angle, then the point is on the angle bisector

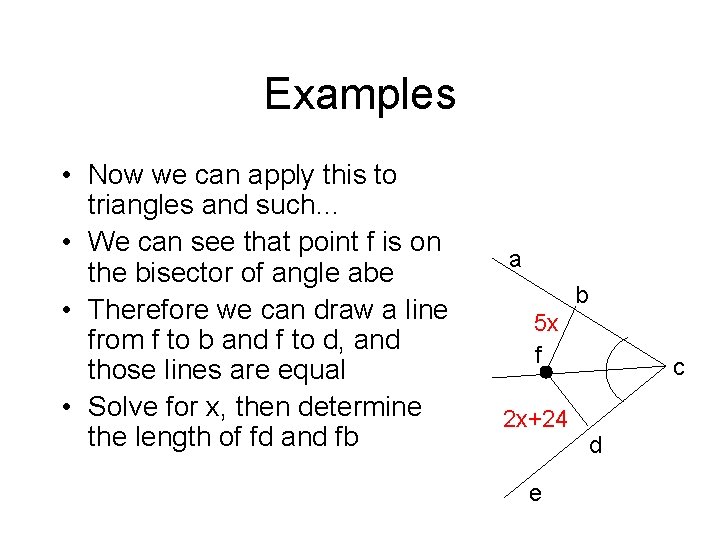
Examples • Now we can apply this to triangles and such… • We can see that point f is on the bisector of angle abe • Therefore we can draw a line from f to b and f to d, and those lines are equal • Solve for x, then determine the length of fd and fb a b 5 x f 2 x+24 e c d

Assignment • P. 296 -297 7, 8, 12 -20 • Worksheet 5 -2

Make a Quiz • Task: You must make a 10 question quiz • This quiz must have questions on: 1. Mid-segments 2. Angle Bisectors 3. Perpendicular Bisectors • You must work with only ONE partner • You must have proper pictures, labels etc. • You must make an answer key, and check all your questions to make sure they work • You will give this test to someone else in this class • You will grade their answers • You have 20 minutes to make this test

Concurrent Lines, Medians, and Altitudes • Question: What do you think the result would be if you bisected all the angles in a triangle? x x x • They all meet in one point • When 3 or more lines intersect in one point, they are considered “concurrent. ” • Therefore the answer is “The lines intersect in a point of concurrency. ” • Theorem - The bisectors of the angles of a triangle are concurrent at a point equidistant from the sides.

Perpendicular Bisectors • Question: What do you think happens if you draw perpendicular bisectors for the sides of a triangle? x • Answer: they are concurrent, and… x x • The perpendicular bisectors of the sides of a triangle are concurrent at a point equidistant from the vertices (corners)

And how do I find the centers of Circles (a life question)? • How do I find the center of a circle drawn around a triangle? (we call that circumscribed) • Draw perpendicular bisectors (the 3 rd one isn’t required here since the other two intersect exactly at the Remember, we want rd midpoint of the 3 side – to be the exact same because it’s a right triangle) distance from all 3 corners

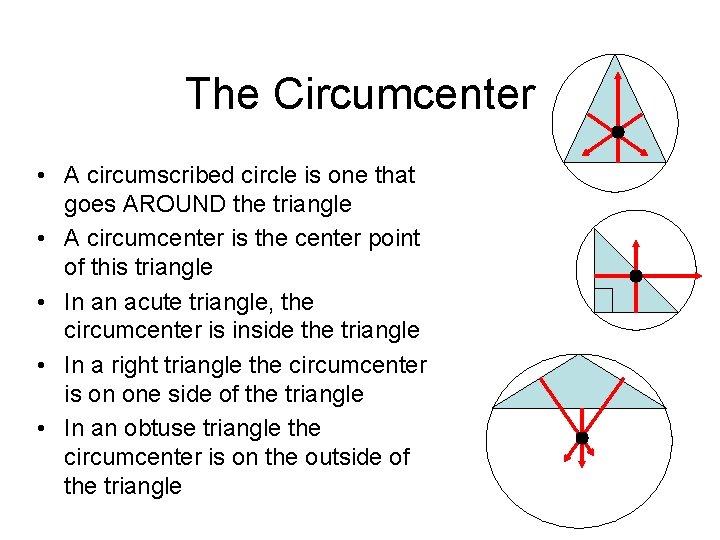
The Circumcenter • A circumscribed circle is one that goes AROUND the triangle • A circumcenter is the center point of this triangle • In an acute triangle, the circumcenter is inside the triangle • In a right triangle the circumcenter is on one side of the triangle • In an obtuse triangle the circumcenter is on the outside of the triangle

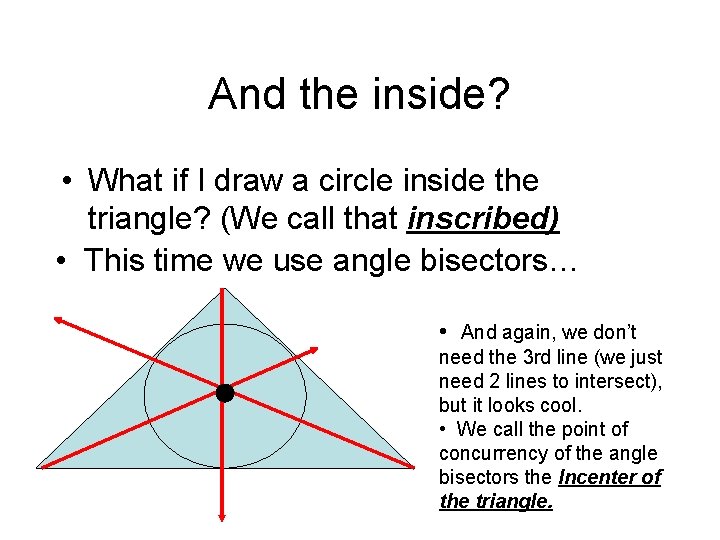
And the inside? • What if I draw a circle inside the triangle? (We call that inscribed) • This time we use angle bisectors… • And again, we don’t need the 3 rd line (we just need 2 lines to intersect), but it looks cool. • We call the point of concurrency of the angle bisectors the Incenter of the triangle.

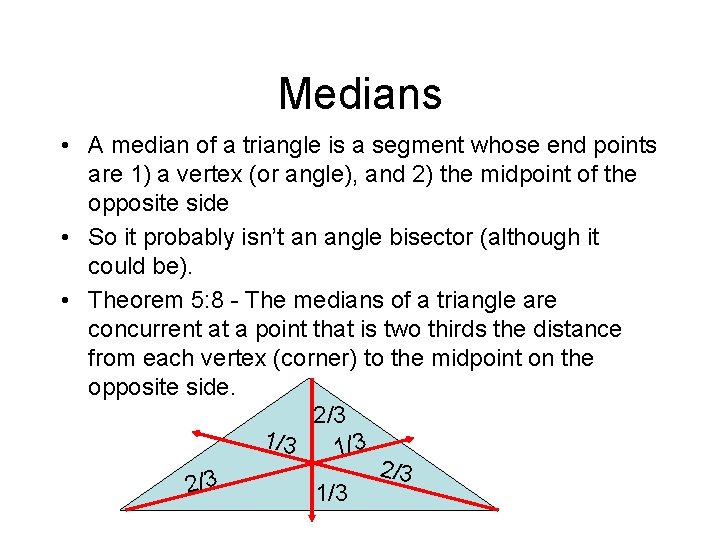
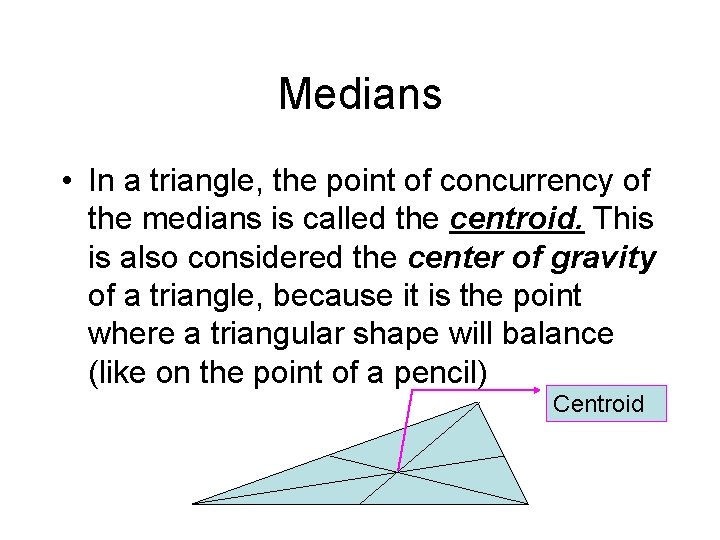
Medians • A median of a triangle is a segment whose end points are 1) a vertex (or angle), and 2) the midpoint of the opposite side • So it probably isn’t an angle bisector (although it could be). • Theorem 5: 8 - The medians of a triangle are concurrent at a point that is two thirds the distance from each vertex (corner) to the midpoint on the opposite side. 2/3 1/3

Medians • In a triangle, the point of concurrency of the medians is called the centroid. This is also considered the center of gravity of a triangle, because it is the point where a triangular shape will balance (like on the point of a pencil) Centroid

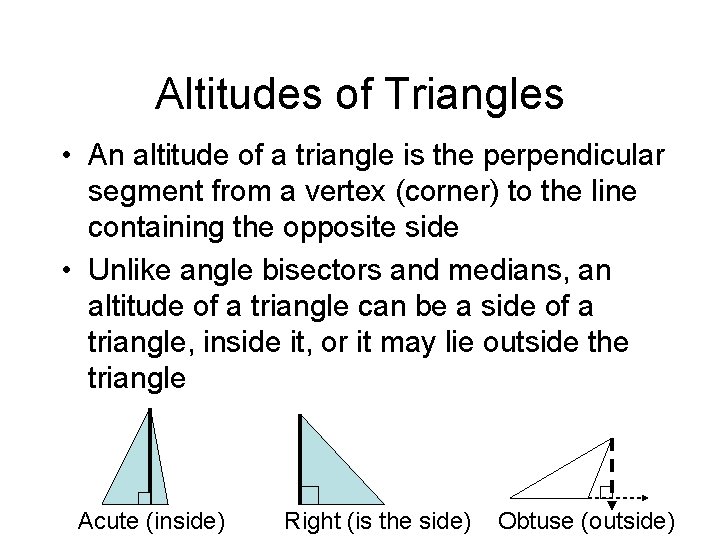
Altitudes of Triangles • An altitude of a triangle is the perpendicular segment from a vertex (corner) to the line containing the opposite side • Unlike angle bisectors and medians, an altitude of a triangle can be a side of a triangle, inside it, or it may lie outside the triangle Acute (inside) Right (is the side) Obtuse (outside)

Assignment • Page 312 8 -13, • Page 313 17 -20, 24 -27 • Worksheet 5 -3

Unit 8 Quiz 2 1. 2. 3. 4. A mid-segment is twice as long as the side it parallels (true/false) An altitude is “how high” a triangle is (true/false) When three points intersect, it is called a point of _____ (fill in blank)? Where three medians of a triangle intersect it is called the _____ (fill in the blank)? 5. The intersection of a) Angle Bisectors, or B) Perpendicular Bisectors is used to find the center point of the circle that goes outside the triangle (A or B)? 6. The intersection of a) Angle Bisectors, or B) Perpendicular Bisectors is used to find the center point of the circle that goes inside the triangle (A or B)? 7. If a circle is inside the triangle, it is called ________ ? (Starts with I) 8. If a circle is outside the triangle, it is called _______ ? (Starts with C) 9. A line that goes from the corner, to the opposite midpoint is called the ________ ? (fill in blank) 10. A median is broken into two lengths, the long length before the median intersects with other medians, and the short length after the intersection of medians. If the length of the median is 9 inches, how long is the long section, and how long is the short section?

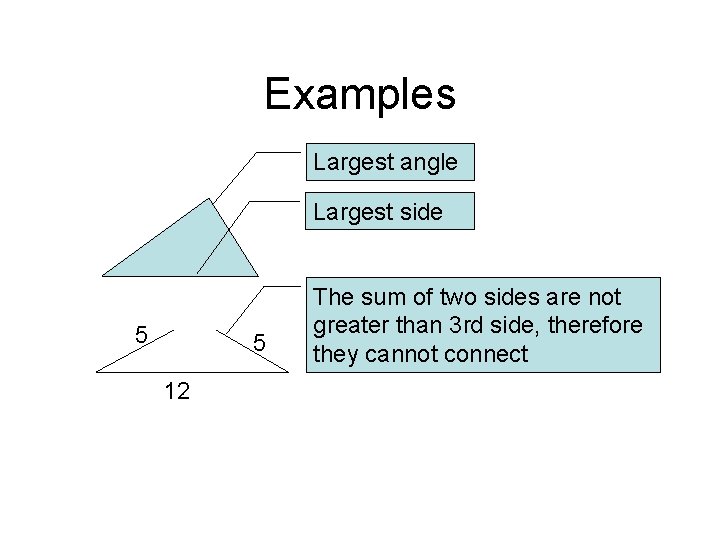
Comparing Sides of a Triangle • If two sides of a triangle are not equal, (congruent) then the largest angle lies opposite the largest side • If two angles of a triangle are not congruent, then the longest side lies opposite the largest angle • The sum of the lengths of any two sides of a triangle must be greater than the length of the third side • These all seem pretty common sense, eh?

Examples Largest angle Largest side 5 5 12 The sum of two sides are not greater than 3 rd side, therefore they cannot connect

Example • Algebra: A triangle has side lengths of 8 cm and 10 cm. Use inequalities to describe possible lengths for the 3 rd side. • Let X = the length of the 3 rd side • Try all three combinations of sides: • X + 8 > 10 or --> X > 2 • X + 10 > 8 or --> X > -2 (not a solution) • 8 + 10 > X or --> X < 18 • Therefore, 2 < X < 18 • The shortcut (whoo hoo!) is this: “Big minus little, Big plus little, put X in the middle…”

Example • A triangle has side lengths of 3 and 12 inches. Describe the lengths possible for the 3 rd side. • X + 3 > 12, so X > 9 • X + 12 > 3, so X > -9 • 3 + 12 > X, so X < 15 • Therefore, 9 < X < 15 • Again, we can just subtract the 2 numbers (as long as I get a positive answer), and add the 2 numbers, and put X in between them.

Assignment • Page 329 9 -32 • Worksheet 5 -5

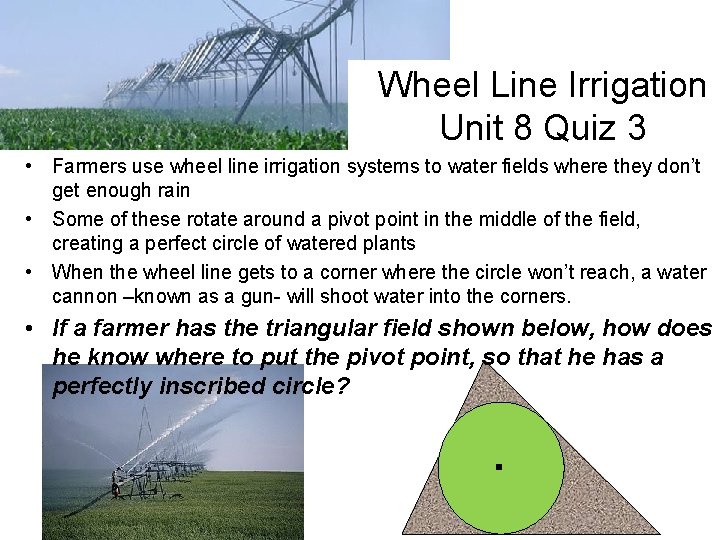
Wheel Line Irrigation Unit 8 Quiz 3 • Farmers use wheel line irrigation systems to water fields where they don’t get enough rain • Some of these rotate around a pivot point in the middle of the field, creating a perfect circle of watered plants • When the wheel line gets to a corner where the circle won’t reach, a water cannon –known as a gun- will shoot water into the corners. • If a farmer has the triangular field shown below, how does he know where to put the pivot point, so that he has a perfectly inscribed circle? .

Congruent Triangles • Question: If you took 3 straws of different lengths (or not, it doesn’t matter), and made a triangle, and took 3 more straws that were exactly the same length, and made another triangle, would it be the same? • Does it have to be the same, or could you make more than one different triangle?

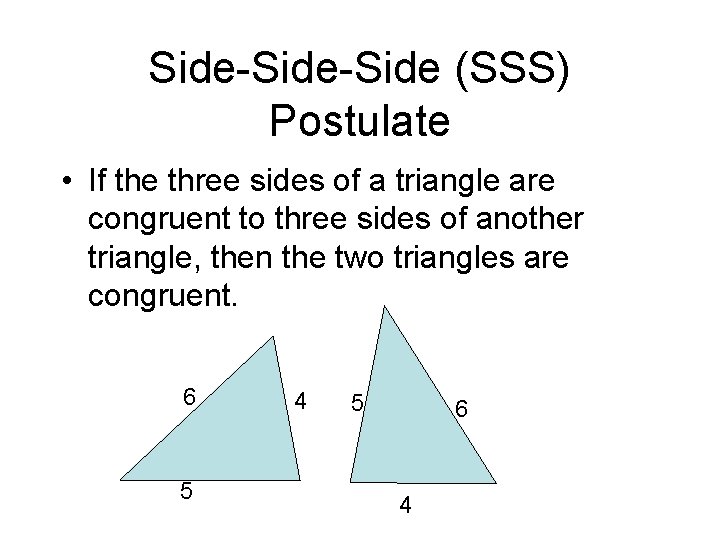
Side-Side (SSS) Postulate • If the three sides of a triangle are congruent to three sides of another triangle, then the two triangles are congruent. 6 5 4 5 6 4

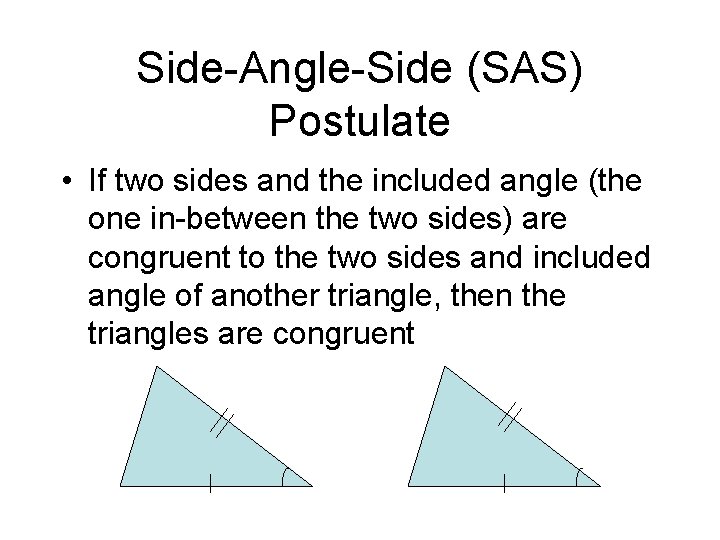
Side-Angle-Side (SAS) Postulate • If two sides and the included angle (the one in-between the two sides) are congruent to the two sides and included angle of another triangle, then the triangles are congruent

Assignment • Page 231 11 -14 • Page 232 24 -26 • Worksheet 4 -2

Unit 8 Quiz 4 • • Miguel wants to make a triangular shaped deck. The side of the deck that runs along the house is called the ledger, and is 15 feet long. The second side of the deck angles out from the house, and is 10 feet long. Miguel is trying to figure out the third side of the deck. He wants to make third side with just one board. Draw a picture (2 points) Label the picture with all information (2 points) 1. 2. • • How short can this board be and still make a triangle? (2 points) How long can this board be and still make a triangle? (2 points) Hint: Since he doesn’t know how long, Miguel calls the length of the board “X” Put your name on the paper (2 points)

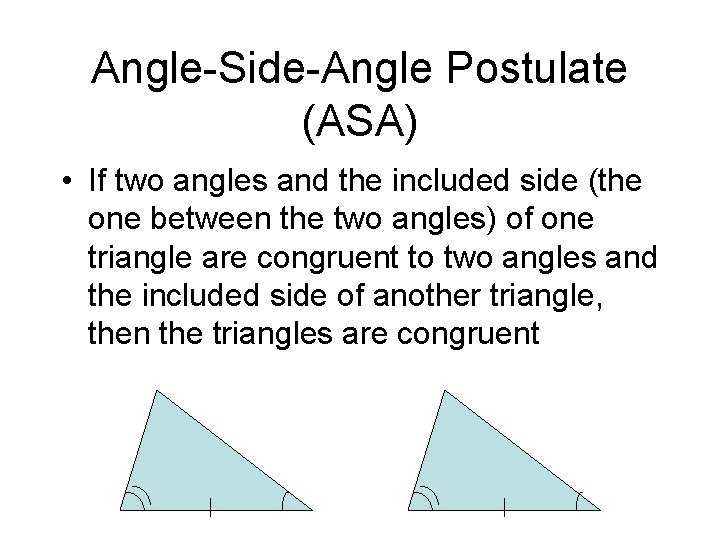
Angle-Side-Angle Postulate (ASA) • If two angles and the included side (the one between the two angles) of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent

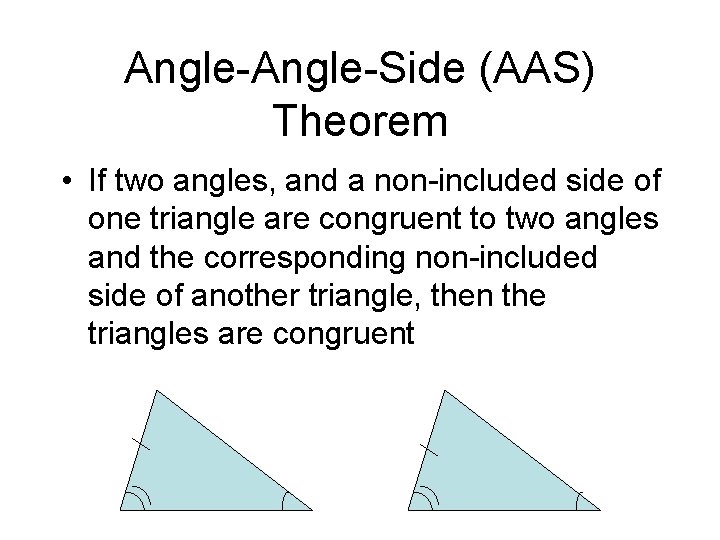
Angle-Side (AAS) Theorem • If two angles, and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent

Assignment • • Page 238 8 -9 Page 239 16 -18 Page 243 6 -11 Worksheet 4 -3

Using Congruent Triangles: (CPCTC) • We used SSS, SAS, ASA, and AAS to show that triangles are congruent • We could then draw conclusions about other parts of the triangles, because by definition all parts of congruent triangles are congruent. • We will call this “corresponding parts of congruent triangles are congruent” or CPCTC

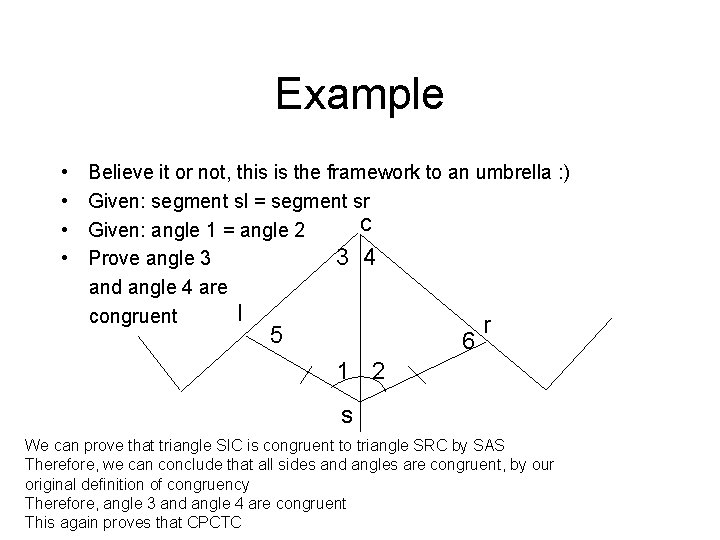
Example • • Believe it or not, this is the framework to an umbrella : ) Given: segment sl = segment sr c Given: angle 1 = angle 2 3 4 Prove angle 3 and angle 4 are l congruent r 5 6 1 2 s We can prove that triangle SIC is congruent to triangle SRC by SAS Therefore, we can conclude that all sides and angles are congruent, by our original definition of congruency Therefore, angle 3 and angle 4 are congruent This again proves that CPCTC

Hypotenuse Leg (HL) Congruency in Right Triangles • Theorem 4: 6 -If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent. (HL)

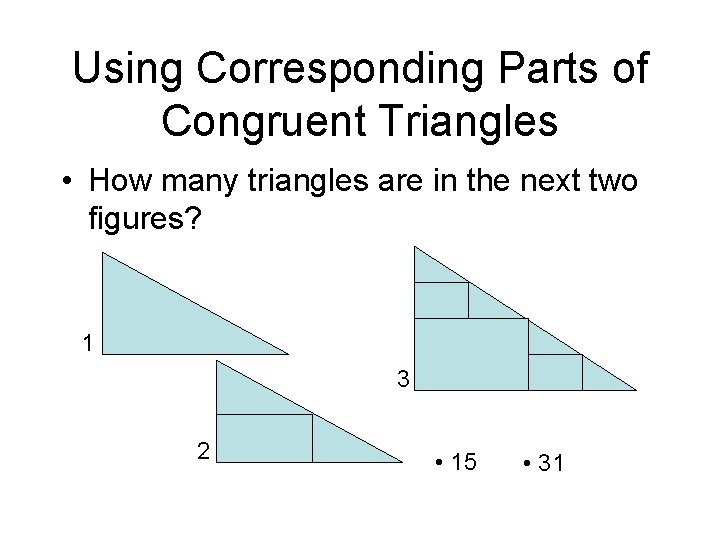
Using Corresponding Parts of Congruent Triangles • How many triangles are in the next two figures? 1 3 2 • 15 • 31

Identifying Common Parts • The idea behind this whole section (as seen on the last slide) is that triangles may share sides or angles. • You need to identify these shared sides and angles • Sometimes you have to pull these triangles apart to see the relationship

Assignment • • • Page 261 1 -4 Page 262 12, 13 Worksheet 4 -4 Worksheet 4 -6 Worksheet 4 -7

Similarity Introduction • Previously, we learned how to prove triangles congruent • Now we will look at how to prove triangles are similar • As a reminder, by definition triangles are similar if they have congruent angles, and sides which have a uniform similarity ratio

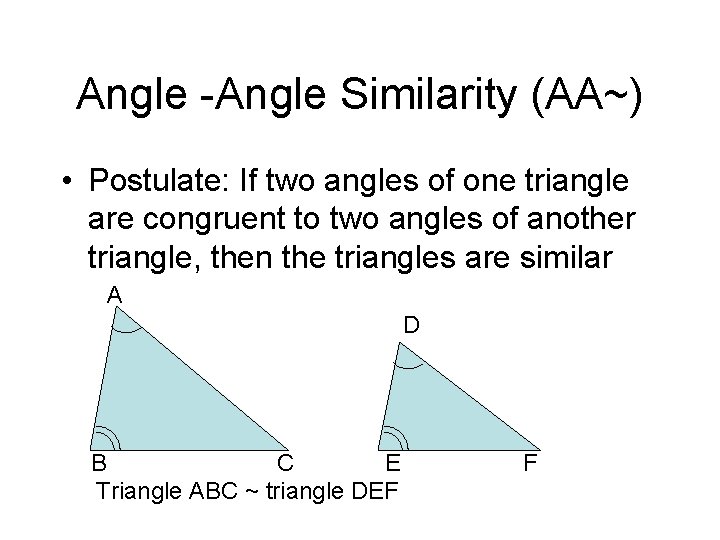
Angle -Angle Similarity (AA~) • Postulate: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar A D B C E Triangle ABC ~ triangle DEF F

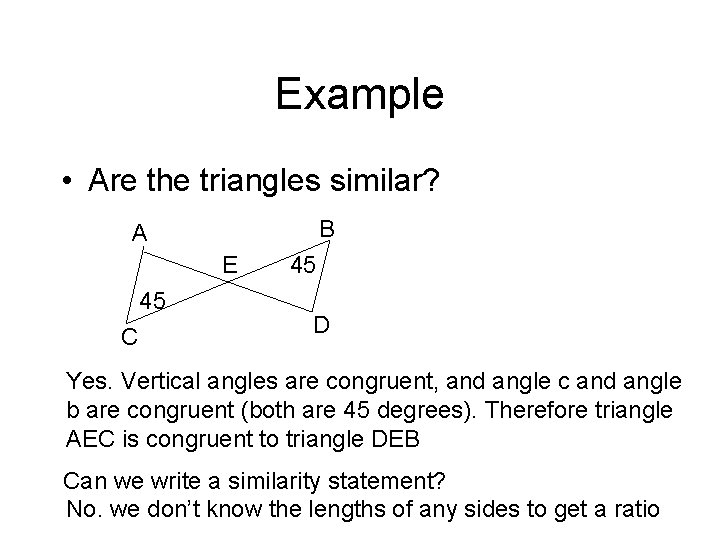
Example • Are the triangles similar? B A E 45 C 45 D Yes. Vertical angles are congruent, and angle c and angle b are congruent (both are 45 degrees). Therefore triangle AEC is congruent to triangle DEB Can we write a similarity statement? No. we don’t know the lengths of any sides to get a ratio

Side Angle Side Similarity (SAS ~) • If an angle of one triangle is congruent to an angle of a second triangle, and the sides which are connected to each angle are proportional, then the triangles are similar

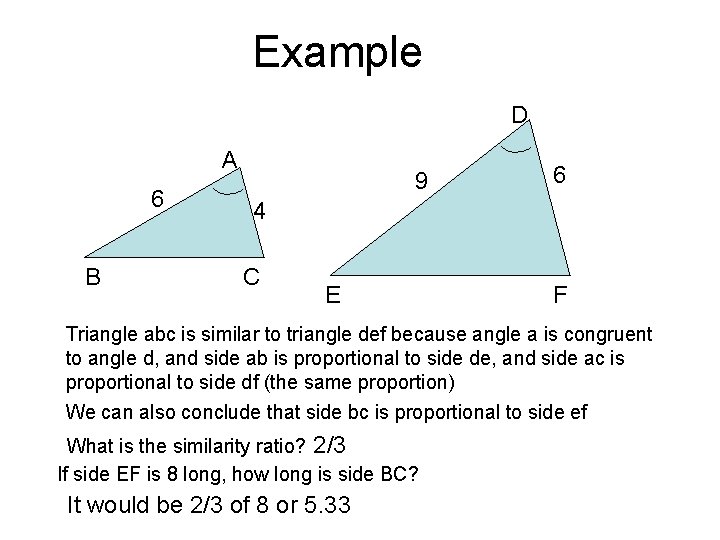
Example D A 6 B 9 6 4 C E F Triangle abc is similar to triangle def because angle a is congruent to angle d, and side ab is proportional to side de, and side ac is proportional to side df (the same proportion) We can also conclude that side bc is proportional to side ef What is the similarity ratio? 2/3 If side EF is 8 long, how long is side BC? It would be 2/3 of 8 or 5. 33

Side-Side Similarity (SSS ~) • If the corresponding sides of two triangles are proportional, then the triangles are similar • Again, this makes sense. If all sides are in proportion, then the angles will necessarily be equal, which is the definition of similar • No matter how you try to put the second triangle together, it will only fit one way, and that way will produce a similar triangle

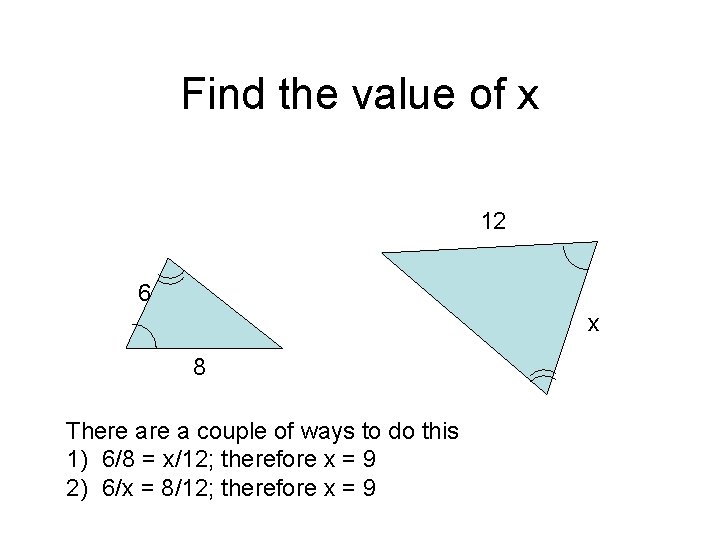
Find the value of x 12 6 x 8 There a couple of ways to do this 1) 6/8 = x/12; therefore x = 9 2) 6/x = 8/12; therefore x = 9

Assignment • Page 455 7 -12 • Page 457 24 -26 • Worksheet 8 -3

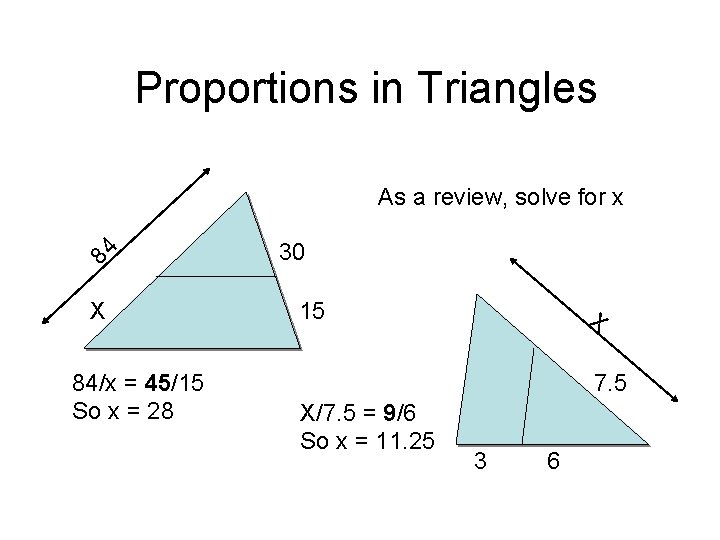
Proportions in Triangles 84 As a review, solve for x X 84/x = 45/15 So x = 28 30 15 X 7. 5 X/7. 5 = 9/6 So x = 11. 25 3 6

Side Splitter Theorem • If a line is parallel to one side of a triangle and intersects the other two sides, then it divides the sides proportionally

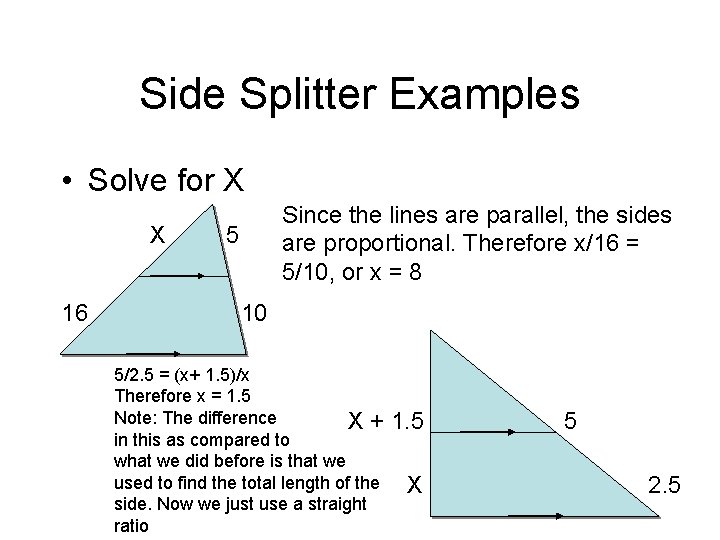
Side Splitter Examples • Solve for X X 16 Since the lines are parallel, the sides are proportional. Therefore x/16 = 5/10, or x = 8 5 10 5/2. 5 = (x+ 1. 5)/x Therefore x = 1. 5 Note: The difference X+ in this as compared to what we did before is that we used to find the total length of the side. Now we just use a straight ratio 1. 5 X 5 2. 5

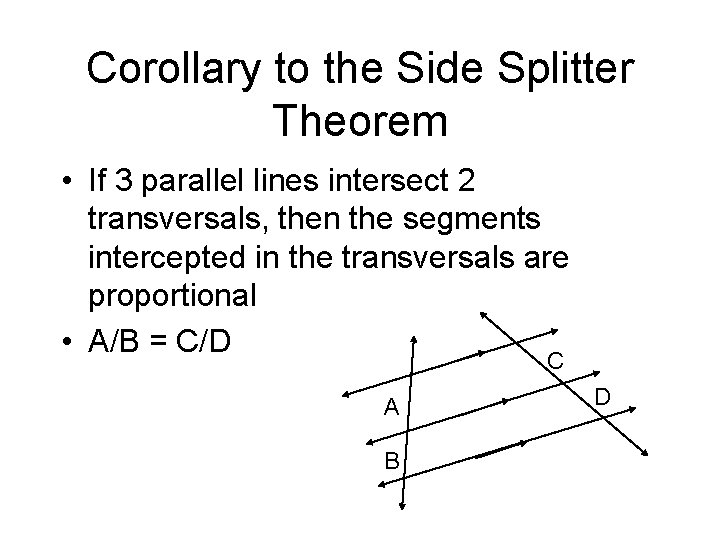
Corollary to the Side Splitter Theorem • If 3 parallel lines intersect 2 transversals, then the segments intercepted in the transversals are proportional • A/B = C/D C A B D

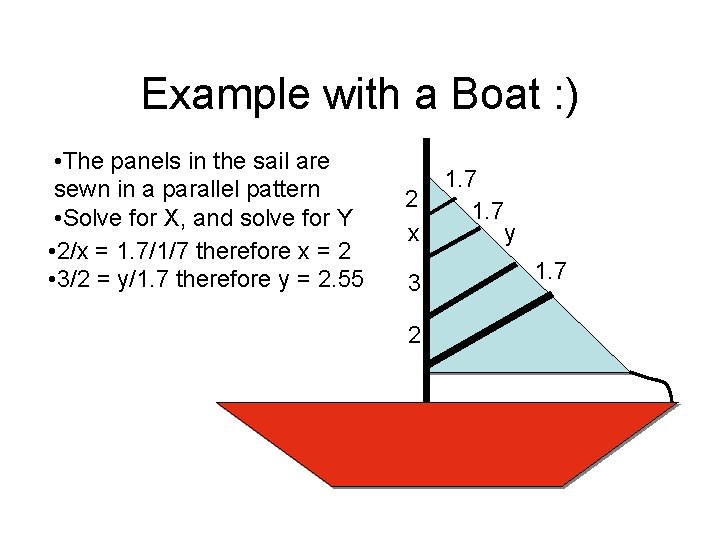
Example with a Boat : ) • The panels in the sail are sewn in a parallel pattern • Solve for X, and solve for Y • 2/x = 1. 7/1/7 therefore x = 2 • 3/2 = y/1. 7 therefore y = 2. 55 2 x 3 2 1. 7 y 1. 7

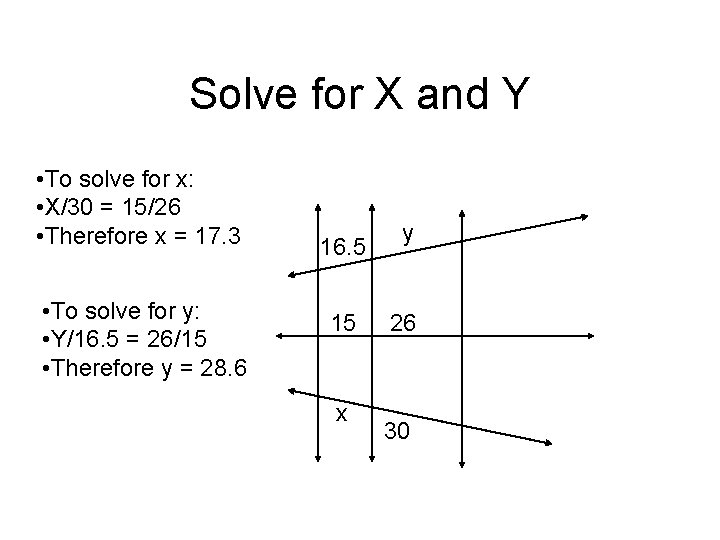
Solve for X and Y • To solve for x: • X/30 = 15/26 • Therefore x = 17. 3 • To solve for y: • Y/16. 5 = 26/15 • Therefore y = 28. 6 16. 5 15 x y 26 30

Triangle-Angle-Bisector Theorem • If a ray bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the other two sides of the triangle

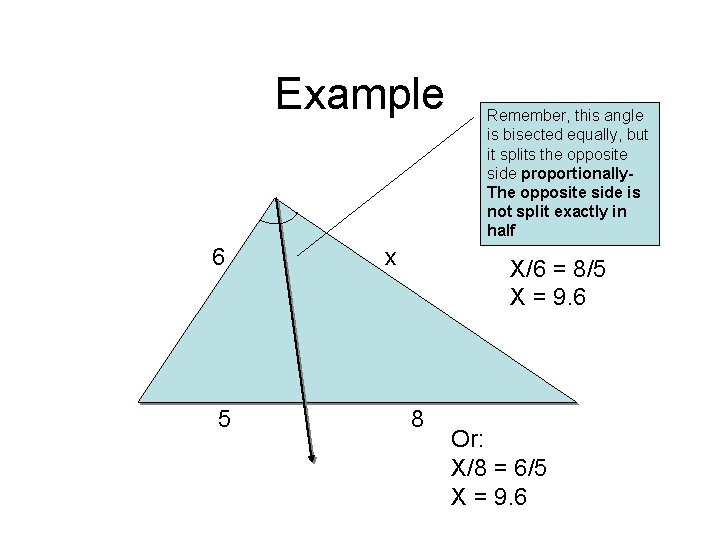
Example 6 5 x Remember, this angle is bisected equally, but it splits the opposite side proportionally. The opposite side is not split exactly in half X/6 = 8/5 X = 9. 6 8 Or: X/8 = 6/5 X = 9. 6

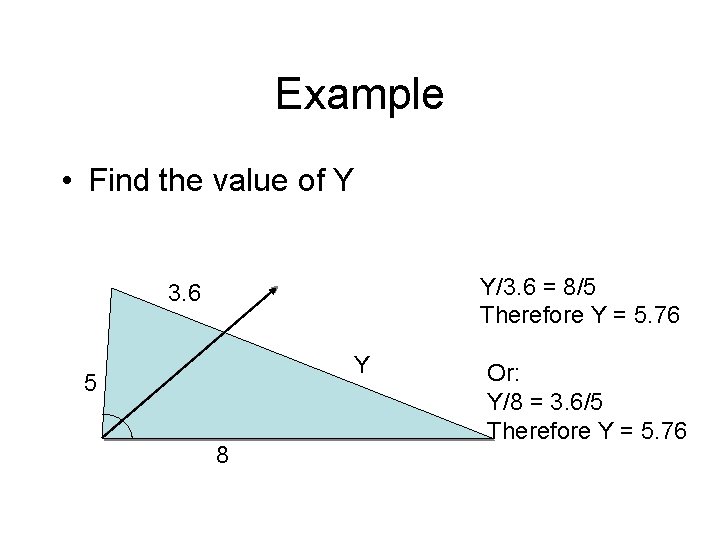
Example • Find the value of Y Y/3. 6 = 8/5 Therefore Y = 5. 76 3. 6 Y 5 8 Or: Y/8 = 3. 6/5 Therefore Y = 5. 76

Assignment • Page 475 9 -22 • Page 476 25 -35 • Worksheet 8 -5

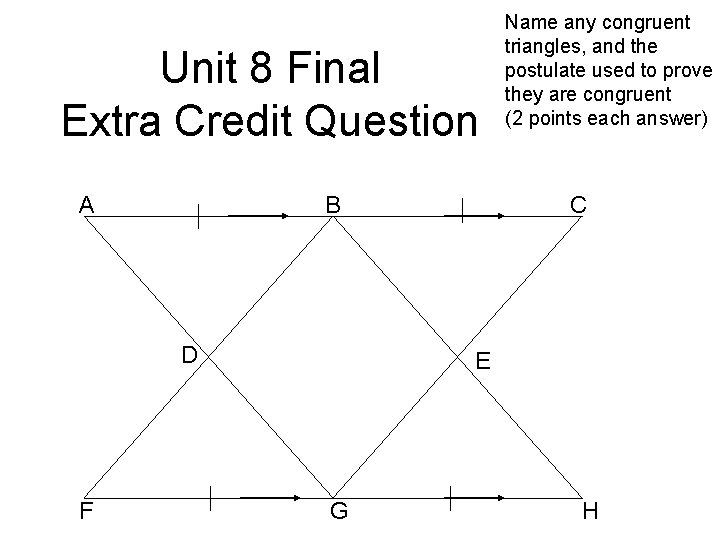
Unit 8 Final Extra Credit Question B A D F Name any congruent triangles, and the postulate used to prove they are congruent (2 points each answer) C E G H