Unit 8 Modeling with Trigonometric Functions Mathematics 3


















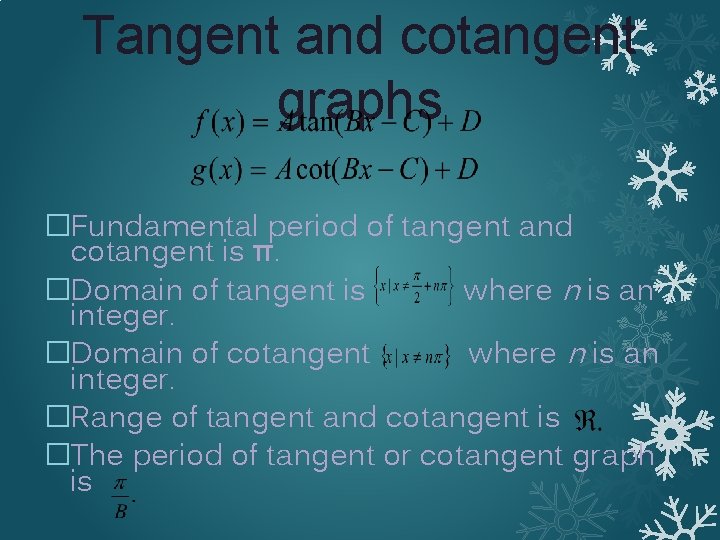

























- Slides: 54

Unit 8: Modeling with Trigonometric Functions Mathematics 3 Ms. C. Taylor

Warm-Up �


The ratios have names & abbreviations… Ratio Name sine Abbreviation sin cosine cos tangent tan cotangent secant cot sec csc

The Trigonometric (trig) ratios: FUNCTION INVERSE FUNCTION

Also true are…

In the ratios: � x is an angle (not the 90 degree angle) � “adjacent”, “opposite” and “hypotenuse” are all side lengths, not angles � “Adjacent” is the side next to the known angle � “Opposite” is the side across from the known angle

!IMPORTANT! To solve trig functions in the calculator, make sure to set your MODE to DEGREES �Directions: Press MODE, arrow down to Radian Arrow over to Degrees Press ENTER

Warm-Up

Measuring Angles The measure of an angle is determined by the amount of rotation from the initial side to the terminal side. There are two common ways to measure angles, in degrees and in radians. We’ll start with degrees, denoted by the symbol º. One degree (1º) is equivalent to a rotation of revolution. 10 of one

Measuring Angles

Radian Measure Definition of Radian: One radian is the measure of a central angle that intercepts arc s equal in length to the radius r of the circle. In general,

Conversions Between Degrees and Radians 1. To convert degrees to radians, multiply degrees by 2. To convert radians to degrees, multiply radians by

Ex 5. Convert the degrees to radian measure. a) 60 b) 30 c) -54 d) -118 e) 45

Ex 6. Convert the radians to degrees. a) b) c) d)

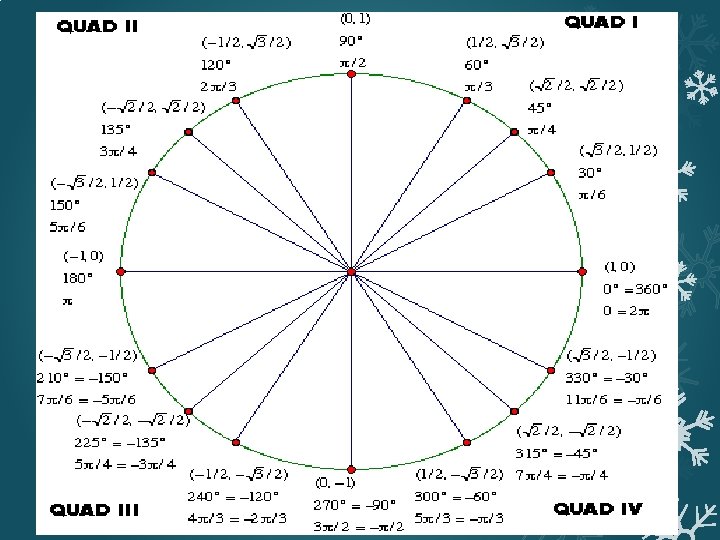
Unit circle �Radius of the circle is 1. �x = cos(θ) �y = sin(θ) �Pythagorean Theorem: �This gives the identity: �Zeros of sin(θ) are �Zeros of cos(θ) are where n is an integer.


Warm-Up

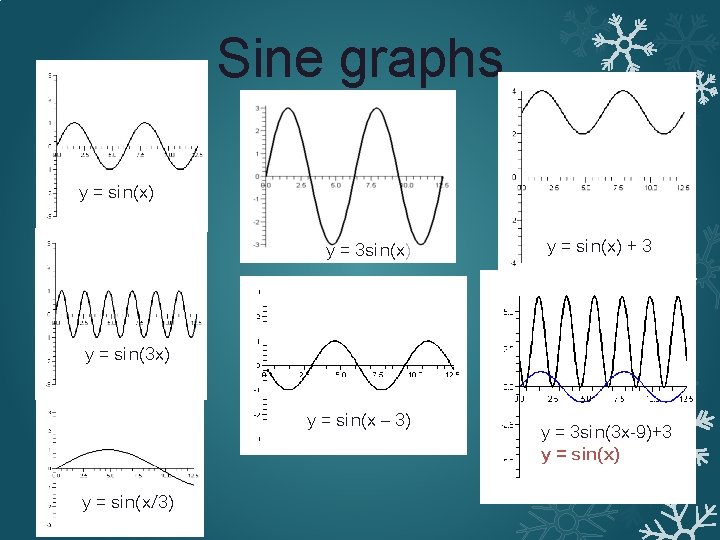
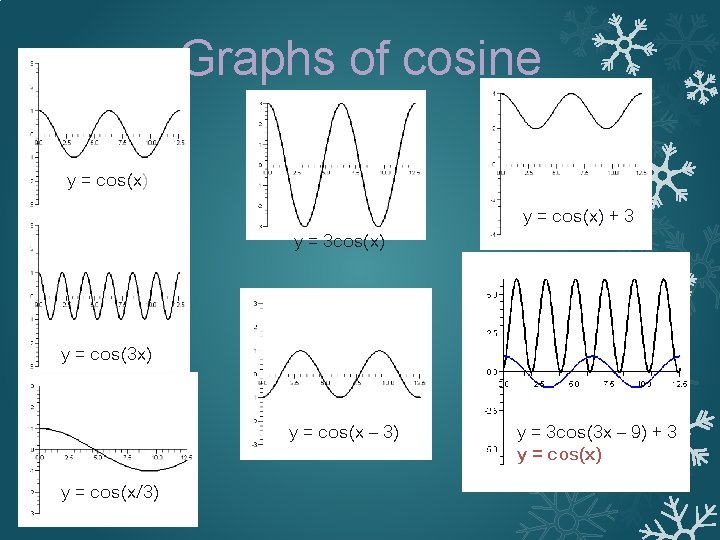
Graphs of sine & cosine �Fundamental period of sine and cosine is 2π. �Domain of sine and cosine is �Range of sine and cosine is [–|A|+D, |A|+D]. �The amplitude of a sine and cosine graph is |A|. �The vertical shift or average value of sine and cosine graph is D. �The period of sine and cosine graph is �The phase shift or horizontal shift is

Sine graphs y = sin(x) y = 3 sin(x) y = sin(x) + 3 y = sin(3 x) y = sin(x – 3) y = sin(x/3) y = 3 sin(3 x-9)+3 y = sin(x)

Graphs of cosine y = cos(x) y = 3 cos(x) y = cos(x) + 3 y = cos(3 x) y = cos(x – 3) y = cos(x/3) y = 3 cos(3 x – 9) + 3 y = cos(x)
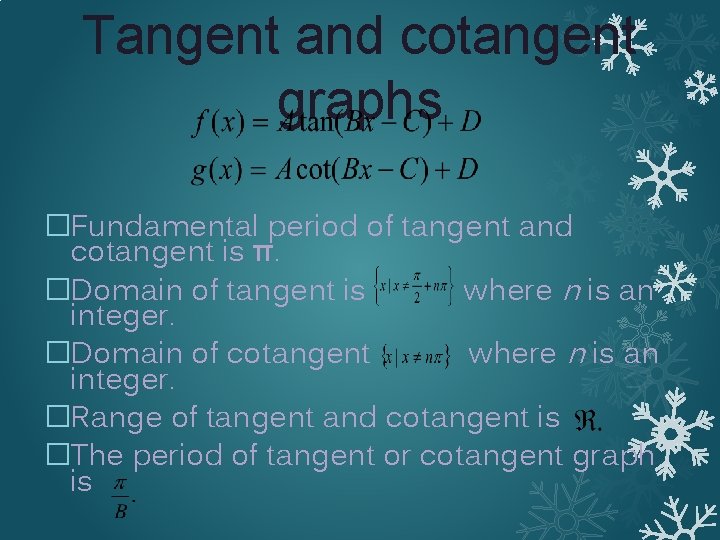
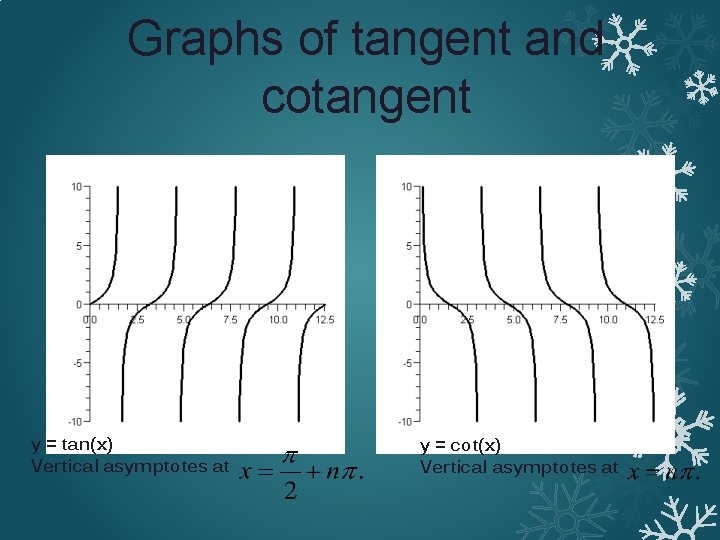
Tangent and cotangent graphs �Fundamental period of tangent and cotangent is π. �Domain of tangent is where n is an integer. �Domain of cotangent where n is an integer. �Range of tangent and cotangent is �The period of tangent or cotangent graph is

Graphs of tangent and cotangent y = tan(x) Vertical asymptotes at y = cot(x) Vertical asymptotes at

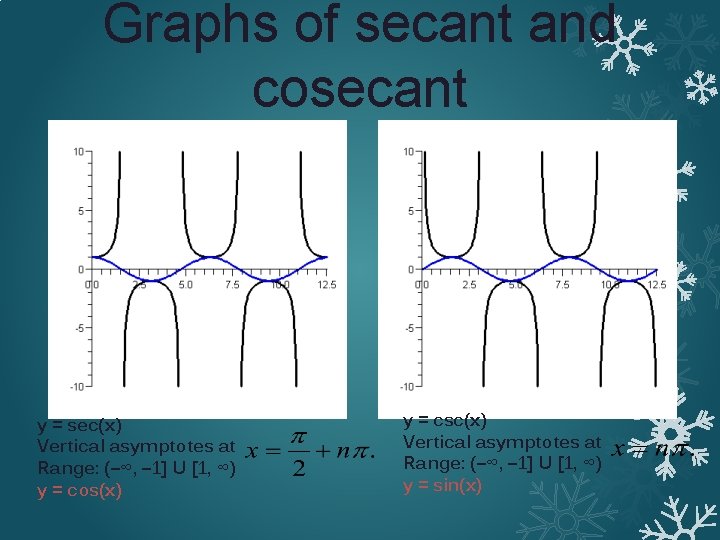
Graphs of secant and cosecant y = sec(x) Vertical asymptotes at Range: (–∞, – 1] U [1, ∞) y = cos(x) y = csc(x) Vertical asymptotes at Range: (–∞, – 1] U [1, ∞) y = sin(x)

Warm-Up

re did our Pythagorean identities come from Do you remember the Unit Circle? � What is the equation for the unit circle? x 2 + y 2 = 1 • What does x = ? What does y = ? (in terms of trig functions) sin 2θ + cos 2θ = 1 Pythagorean Identity!

Take the Pythagorean Identity and discover a new one! Hint: Try dividing everything by cos 2θ sin 2θ + cos 2θ = 1. cos 2θ tan 2θ + 1 = sec 2θ Quotient Identity another Pythagorean Identity Reciprocal Identity

Take the Pythagorean Identity and discover a new one! Hint: Try dividing everything by sin 2θ + cos 2θ = 1. sin 2θ 1 + cot 2θ = csc 2θ Quotient Identity a third Pythagorean Identity Reciprocal Identity

Trigonometric Identities Quotient Identities Reciprocal Identities Pythagorean Identities sin 2 q + cos 2 q = 1 tan 2 q + 1 = sec 2 q cot 2 q + 1 = csc 2 q sin 2 q = 1 - cos 2 q tan 2 q = sec 2 q - 1 cot 2 q = csc 2 q - 1 cos 2 q = 1 - sin 2 q

Simplifying trig Identity Example 1: simplify tanxcosx sin x tanx cos x tanxcosx = sin x

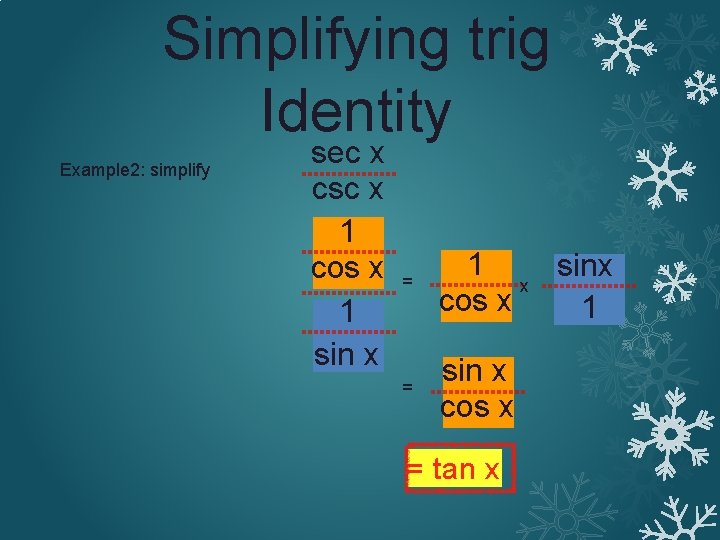
Simplifying trig Identity Example 2: simplify sec x csc x 1 cos sec x csc 1 x sin x = 1 sinx x cos x 1 = sin x cos x = tan x

Example Simplify: = cot x (csc 2 x - 1) Factor out cot x = cot x (cot 2 x) Use pythagorean identi = cot 3 x Simplify

Warm-Up

Types of Angles There are four different types of angles in any given circle. The type of angle is determined by the location of the angles vertex. 1. In the Center of the Circle: Central Angle 2. On the Circle: Inscribed Angle 3. In the Circle: Interior Angle 4. Outside the Circle: Exterior Angle * The measure of each angle is determined by the Intercepted Arc

Intercepted Arc: An angle intercepts an arc if and only if each of the following conditions holds: 1. The endpoints of the arc lie on the angle. 2. All points of the arc, except the endpoints, are in the interior of the angle. 3. Each side of the angle contains an endpoint of the arc.

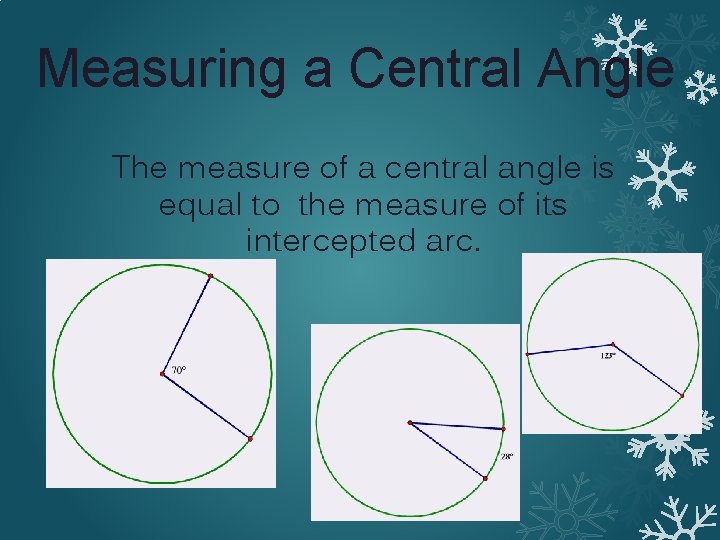
Central Angle Definition: An angle whose vertex lies on the center of the circle. Central Angle (of a circle) NOT A Central Angle (of a circle) * The measure of a central angle is equal to the measure of the intercepted arc.

Measuring a Central Angle The measure of a central angle is equal to the measure of its intercepted arc.

Inscribed Angle: An angle whose vertex lies on a circle and whose sides are chords of the circle (or one side tangent to the circle). Examples: 1 2 No! Yes! 3 No! 4 Yes!

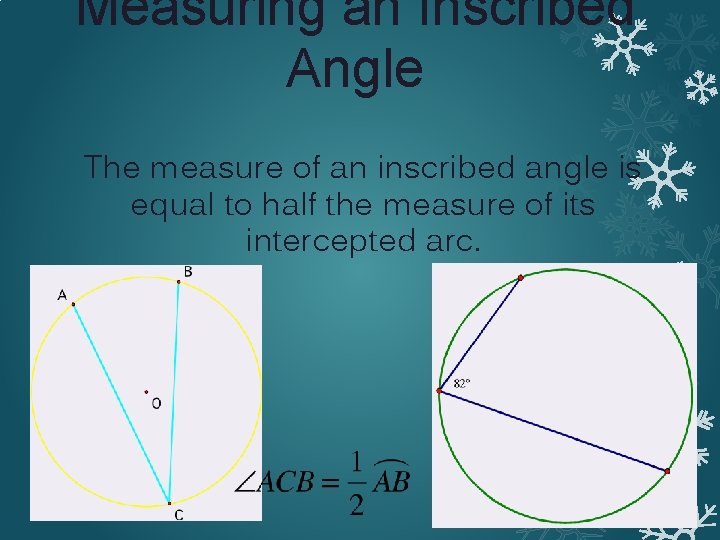
Measuring an Inscribed Angle The measure of an inscribed angle is equal to half the measure of its intercepted arc.

Corollaries If two inscribed angles intercept the same arc, then the angles are congruent.

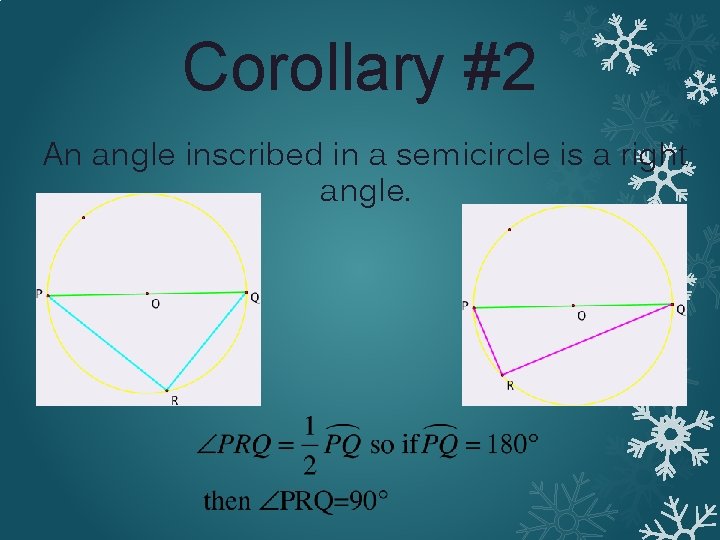
Corollary #2 An angle inscribed in a semicircle is a right angle.

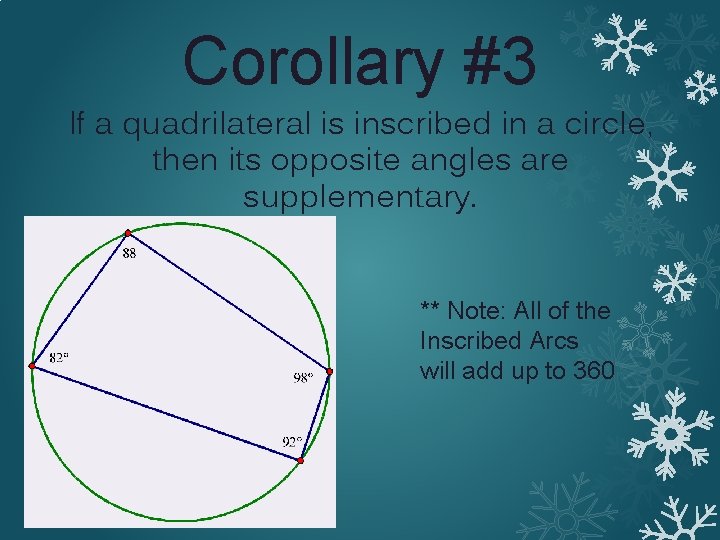
Corollary #3 If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary. ** Note: All of the Inscribed Arcs will add up to 360

Warm-Up

Area of a Sector Formula measure of the central angle or arc Area of a sector = m 2 πr 360 The area of the entire circle! The fraction of the circle! .

6. The area of sector AOB is 48π and Area of a sector = m πr 2 360 270 48π = πr 2 360 4 16 3 4 48 = r 2 3 4 3 64 = r 2 r=8 . Find the radius of ○O.

7. The area of sector AOB is Area of a sector = and m πr 2 360 9 40 π= πr 2 4 360 99 1 2 9 = r 1 4 9 1 81 2 = r 4 r= 9 2 . Find the radius of ○O.

The standard form of the equation of a circle with its center at the origin is r is the radius of the circle so if we take the square root of the right hand side, we'll know how big the radius is. Notice that both the x and y terms are squared. Linear equations don’t have either the x or y terms squared. Parabolas have only the x term was squared (or only the y term, but NOT both).

Let's look at the equation This is r 2 so r = 3 The center of the circle is at the origin and the radius is 3. Let's graph this circle. Count out 3 in all directions since that is the radius Center at (0, 0) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

If the center of the circle is NOT at the origin the equation for the standard form of a circle looks like this: The center of the circle is at (h, k). This is r 2 so r = 4 Find the center and radius and graph this circle. The center of the circle is at (h, k) which is (3, 1). The radius is 4 - - - - 12345678 765432 1 0

If you take the equation of a circle in standard form for example: This is r 2 so r = 2 (x - (-2)) Remember center is at (h, k) with (x - h) and (y - k) since the x is plus something and not minus, (x + 2) can be written as (x - (-2)) You can find the center and radius easily. The center is at (-2, 4) and the radius is 2. But what if it was not in standard form but multiplied out (FOILED) Moving everything to one side in descending order and combining like terms we'd have:

If we'd have started with it like this, we'd have to complete the square on both the x's and y's to get in standard form. Group x terms and a Group y terms and a place to complete the square 4 16 Complete the square Write factored and wahlah! back in standard form. Move constant to the other side 4 16

Warm-Up

Warm-Up

Law of Sines & Law of Cosines Law of sines Use when you have a complete ratio: SSA. Law of cosines Use when you have SAS, SSS.