Unit 8 Final Review 1 Final Exam Review

















































































- Slides: 115

Unit 8: Final Review 1. Final Exam Review Sta 101 - Fall 2018 Duke University, Department of Statistical Science Dr. Ellison Slides posted at https: //www 2. stat. duke. edu/courses/Fall 18/sta 101. 001/

Outline 1. Housekeeping 2. Review

Announcements This week: • Monday and Wednesday Lectures: Final Exam Review • Submit Project Presentation slides, rmd, and html files on Sakai Wednesday 12/5 11: 59 pm. • Project Presentations in your Lab 12/6 • Teacher evaluations in Lab 12/6 (Extra credit if we get 80% of class to participate) Final Office Hours • Final day of TA office hours is this Thursday • My office hours Fridays 12/7 and 12/14 • Another review session (Doodle poll)? Final Exam: • Sunday 12/16 2: 00 pm-5: 00 pm 1

Final Exam Announcemen ts • Exam • written questions (like • Material Covered: AEs) • Units 1 -7 • Fill in the blank • Slightly higher emphasis on questions Units 6 and 7 • 10 T/F • What to bring: • 10 MC • Cheat sheet • 1 page (8. 5’’ by 11’’) • Front/back ok • CAN be typed • Calculator (no phones) • Provided: • Z-tables, t-tables, Chi-Squaredtables 1

Final Review Suggestions Announcemen ts • Short answer review: • Make sure you understand how to do the application exercises. • Review Problem Sets (graded) • Short answer practice: • Practice test • Suggested practice problems in the book • Lab Review tomorrow 1

Final Review Suggestions Announcemen ts • Concept review: • Video notes: • Lecture slides (has material not in the videos/book): • Readiness Assessments+Performance Assessments: • Why are all the other options wrong? • What to think about (among other things): • Interpretations of analyses (WORDING IS IMPORTANT) • Conclusions we would make (WORDING IS IMPORTANT) • Relationships between different analyses • Know exact definitions • FOCUS ON THE WHY BEHIND ANALYSES • If there’s an equation/analysis, make sure you know how to put that equation/analysis into words in the context of the problem. • Common misconceptions (lecture notes) • What test to use under certain conditions 1

Outline 1. Housekeeping 2. Review

Outline

Clicker question A recent research study randomly divided participants into groups who were told that they were given different levels of Vitamin E to take daily. Actually, one group received only a placebo pill, and the other received Vitamin E. The research study followed the participants for eight years to see how many developed a particular type of cancer during that time period. Which of the following responses gives the best explanation as to the purpose of the random assignment in this study? Bayesian inference Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median two means & medians categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) To prevent skewness in the results. (b) To reduce the amount of sampling variability. (c) To ensure that all potential cancer patients had an equal chance of being selected for the study. (d) To produce treatment groups with similar characteristics. (e) To ensure that the sample is representative of all cancer patients. 2

Clicker question A recent research study randomly divided participants into groups who were told that they were given different levels of Vitamin E to take daily. Actually, one group received only a placebo pill, and the other received Vitamin E. The research study followed the participants for eight years to see how many developed a particular type of cancer during that time period. Which of the following responses gives the best explanation as to the purpose of the random assignment in this study? Bayesian inference Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median two means & medians categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) To prevent skewness in the results. (b) To reduce the amount of sampling variability. (c) To ensure that all potential cancer patients had an equal chance of being selected for the study. (d) To produce treatment groups with similar characteristics. (e) To ensure that the sample is representative of all cancer patients. 2

Clicker question A recent research study randomly divided participants into groups who were told that they were given different levels of Vitamin E to take daily. Actually, one group received only a placebo pill, and the other received Vitamin E. The research study followed the participants for eight years to see how many developed a particular type of cancer during that time period. Which of the following responses gives the best explanation as to the purpose of the random assignment in this study? Bayesian inference Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median two means & medians categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) To prevent skewness in the results. (b) To reduce the amount of sampling variability. → What could we change to do this? (c) To ensure that all potential cancer patients had an equal chance of being selected for the study. → How do/did we achieve this? (d) To produce treatment groups with similar characteristics. → What other purposes are there? (e) To ensure that the sample is representative of all cancer patients. → How do/did we achieve this? 2

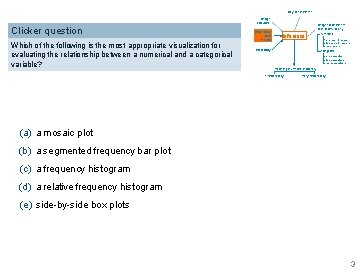
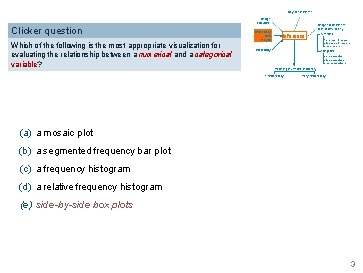
Bayesian inference Design ofstudies Clicker question Which of the following is the most appropriate visualization for evaluating the relationship between a numerical and a categorical variable? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) a mosaic plot (b) a segmented frequency bar plot (c) a frequency histogram (d) a relative frequency histogram (e) side-by-side box plots 3

Bayesian inference Design ofstudies Clicker question Which of the following is the most appropriate visualization for evaluating the relationship between a numerical and a categorical variable? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) a mosaic plot (b) a segmented frequency bar plot (c) a frequency histogram (d) a relative frequency histogram (e) side-by-side box plots 3

Bayesian inference Design ofstudies Clicker question Which of the following is the most appropriate visualization for evaluating the relationship between a numerical and a categorical variable? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) a mosaic plot → (two categorical variables) (b) a segmented frequency bar plot→ (two categorical variables) (c) a frequency histogram → (one numerical variable) (d) a relative frequency histogram → (one numerical variable) (e) side-by-side box plots 3

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Box plots are useful for highlighting outliers, but we cannot determine skew based on a box plot. (b) Median and IQR are more robust statistics than mean and SD, respectively, since they are not affected by outliers or extreme skewness. (c) When the response variable is extremely right skewed, it may be useful to apply a log transformation to obtain a more symmetric distribution, and model the logged data. (d) Segmented frequency bar plots are “good enough” for evaluating the relationship between two categorical variables if the sample sizes are the same for various levels of the explanatory variable. 4

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Box plots are useful for highlighting outliers, but we cannot determine skew based on a box plot. (b) Median and IQR are more robust statistics than mean and SD, respectively, since they are not affected by outliers or extreme skewness. (c) When the response variable is extremely right skewed, it may be useful to apply a log transformation to obtain a more symmetric distribution, and model the logged data. (d) Segmented frequency bar plots are “good enough” for evaluating the relationship between two categorical variables if the sample sizes are the same for various levels of the explanatory variable. 4

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Box plots are useful for highlighting outliers, but we cannot determine skew based on a box plot. → What aspect of shape can we not determine from a boxplot? (b) Median and IQR are more robust statistics than mean and SD, respectively, since they are not affected by outliers or extreme skewness. → Why is this? (c) When the response variable is extremely right skewed, it may be useful to apply a log transformation to obtain a more symmetric distribution, and model the logged data (Slides 7. 2) (d) Segmented frequency bar plots are “good enough” for evaluating the relationship between two categorical variables if the sample sizes are the same for various levels of the explanatory variable. → (See graph) 4

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) If A and B are independent, then having information on A does not tell us anything about B. (b) If A and B are disjoint, then knowing that A occurs tells us that B cannot occur. (c) Disjoint (mutually exclusive) events are always dependent since if one event occurs we know the other one cannot. (d) If A and B are independent, then P(A and B) = P(A) + P(B). (e) If A and B are not disjoint, then P(A or B) = P(A) + P(B) - P(A and B). 5

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) If A and B are independent, then having information on A does not tell us anything about B. (b) If A and B are disjoint, then knowing that A occurs tells us that B cannot occur. (c) Disjoint (mutually exclusive) events are always dependent since if one event occurs we know the other one cannot. (d) If A and B are independent, then P(A and B) = P(A) + P(B). (e) If A and B are not disjoint, then P(A or B) = P(A) + P(B) - P(A and B). 5

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) If A and B are independent, then having information on A does not tell us anything about B. → Which independent variables equation is most helpful for showing this property? (b) If A and B are disjoint, then knowing that A occurs tells us that B cannot occur. → Disjoint means P(A and B) = 0 (c) Disjoint (mutually exclusive) events are always dependent since if one event occurs we know the other one cannot. → Disjoint means P(A and B) = 0 P(A) × P(B). (d) If A and B are independent, then P(A and B) = P(A) + P(B). (e) If A and B are not disjoint, then P(A or B) = P(A) + P(B) - P(A and B). 5

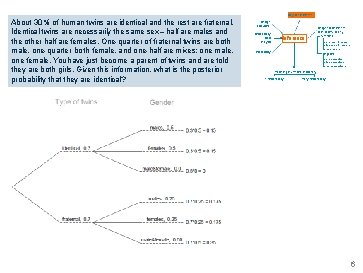
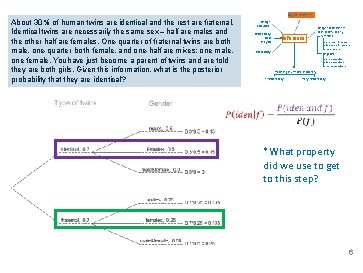
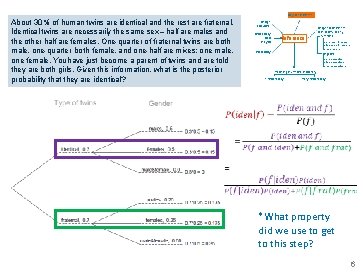
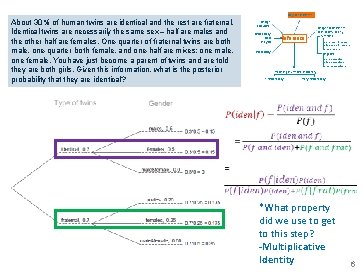
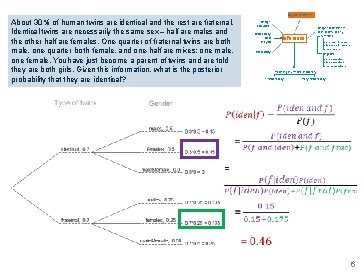
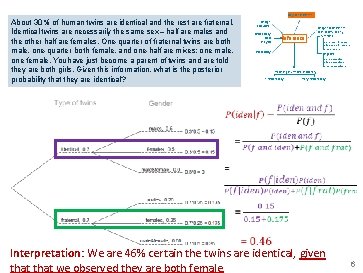
Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory 6

Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory 6

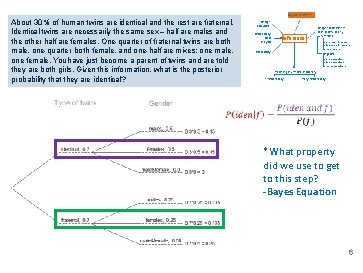
Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory *What property did we use to get to this step? 6

Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory *What property did we use to get to this step? -Bayes Equation 6

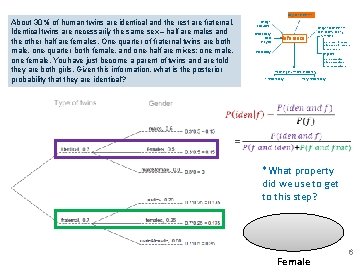
Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory *What property did we use to get to this step? Female 6

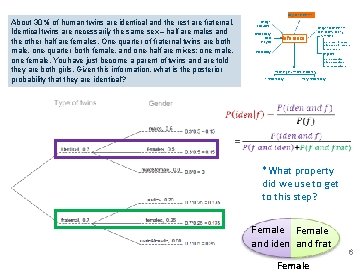
Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory *What property did we use to get to this step? Female and iden and frat Female 6

Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory *What property did we use to get to this step? 6

Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory *What property did we use to get to this step? -Multiplicative Identity 6

Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory 6

Bayesian inference About 30% of human twins are identical and the rest are fraternal. Identical twins are necessarily the same sex – half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the posterior probability that they are identical? Design ofstudies Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory Interpretation: We are 46% certain the twins are identical, given that we observed they are both female. 6

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Suppose you’re evaluating 4 claims. If prior to data collection you don’t have a preference for one claim over another, you should assign 0. 25 as the prior probability to each claim. (b) Posterior probability and the p-value are the equivalent. (c) One advantage of Bayesian inference is that data can be integrated to the inferential scheme as they are collected. (d) Suppose a patient tests positive for a disease that 2% of the population are known to have. A doctor wants to confirm the test result by retesting the patient. In the second test the prior probability for “having the disease” should be more than 2%. 7

Bayesian inference Design ofstudies Clicker question Which of the following is false? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Suppose you’re evaluating 4 claims. If prior to data collection you don’t have a preference for one claim over another, you should assign 0. 25 as the prior probability to each claim. (b) Posterior probability and the p-value are the equivalent. (c) One advantage of Bayesian inference is that data can be integrated to the inferential scheme as they are collected. (d) Suppose a patient tests positive for a disease that 2% of the population are known to have. A doctor wants to confirm the test result by retesting the patient. In the second test the prior probability for “having the disease” should be more than 2%. Posterior = P(hypothesis | data), p-value ≈ P(data | hypothesis) 7

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 1: 25 pm section 3: 05 pm section Everyone 8

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 3: 05 pm section Everyone 0. 45 1: 25 pm section 8

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 3: 05 pm section Everyone 0. 45 1: 25 pm section 0. 04 8

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 0. 45 0. 39 1: 25 pm section 3: 05 pm section Everyone 0. 04 8

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 0. 45 0. 39 1: 25 pm section 3: 05 pm section 0. 04 0. 0002 Everyone 8

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 0. 45 0. 39 0. 29 1: 25 pm section 3: 05 pm section Everyone 0. 04 0. 0002 8

Activity: Test the hypothesis H 0 : µ = 10 vs. H A : µ > 10 for the following 6 samples. Assume σ = 2. n = 30 p − value n = 5000 p − value 10. 05 10. 1 10. 2 8: 30 am section 10: 05 am section 11: 45 am section 0. 45 0. 39 0. 29 1: 25 pm section 3: 05 pm section Everyone 0. 04 0. 0002 ≈0 *What relationships between the following does this activity show? • Sample size • How far away sample statistic is away from the null value • Test Statistic • P-value 8

Bayesian inference Design ofstudies Clicker question Which of the following is the best method for evaluating the if the distribution of a categorical variable follows a hypothesized distribution? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) chi-square test of independence (b) chi-square test of goodness of fit (c) anova (d) linear regression (e) t-test 9

Bayesian inference Design ofstudies Clicker question Which of the following is the best method for evaluating the if the distribution of one categorical variable follows a hypothesized distribution? Exploratory data analysis Inference Probability Frequentist inference (CLT & simulation) numerical one mean & median two means & medians many means categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) chi-square test of independence (b) chi-square test of goodness of fit (c) anova (d) linear regression (e) t-test 9

Bayesian inference Clicker question Which of the following is the best method for evaluating the relationship between a numerical and a categorical variable with many levels? Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) z-test (b) chi-square test of goodness of fit (c) anova (d) linear regression (e) t-test 10

Bayesian inference Clicker question Which of the following is the best method for evaluating the relationship between a numerical and a categorical variable with many levels? Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) z-test (b) chi-square test of goodness of fit (c) anova (d) linear regression (e) t-test 10

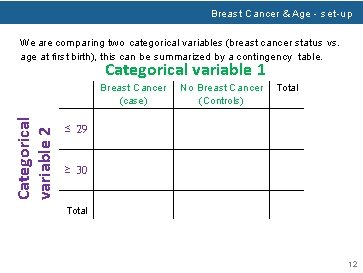
Example - Breast Cancer & Age It is theorized that an important risk factor for breast cancer is age at first birth. An international study was set up to test this hypothesis. Breast-cancer cases were identified among women in selected hospitals in the United States, Greece, Yugoslavia, Brazil, Taiwan, and Japan. Controls were chosen from women of comparable age who were in the hospital at the same time as the cases but who did not have breast cancer. All women were asked about their age at first birth. The set of women with at least one birth was arbitrarily divided into two categories: (1) women whose age at first birth was less than or equal to 29 years and (2) women whose age at first birth was greater than of equal to 30 years. The following results were found among women with at least one birth: 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than or equal to 30. How can we assess whether this difference is significant or simply due to chance? 11

Example - Breast Cancer & Age It is theorized that an important risk factor for breast cancer is age at first birth. An international study was set up to test this hypothesis. Breast-cancer cases were identified among women in selected hospitals in the United States, Greece, Yugoslavia, Brazil, Taiwan, and Japan. Controls were chosen from women of comparable age who were in the hospital at the same time as the cases but who did not have breast cancer. All women were asked about their age at first birth. The set of women with at least one birth was arbitrarily divided into two categories: (1) women whose age at first birth was less than or equal to 29 years and (2) women whose age at first birth was greater than of equal to 30 years. The following results were found among women with at least one birth: 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than or equal to 30. How can we assess whether this difference is significant or simply due to chance? 11

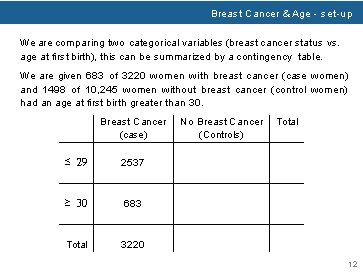
Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. Categorical variable 1 Categorical variable 2 Breast Cancer (case) No Breast Cancer (Controls) Total ≤ 29 ≥ 30 Total 12

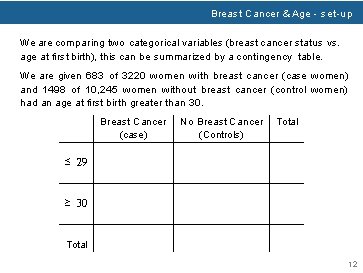
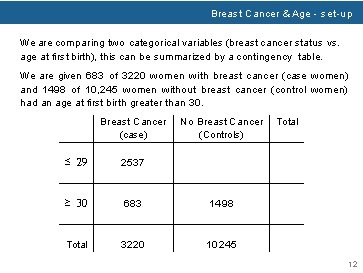
Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. We are given 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than 30. Breast Cancer (case) No Breast Cancer (Controls) Total ≤ 29 ≥ 30 Total 12

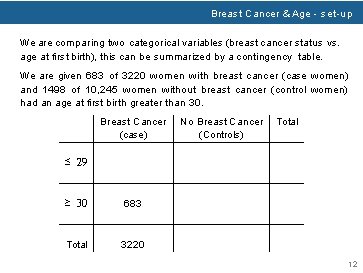
Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. We are given 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than 30. Breast Cancer (case) No Breast Cancer (Controls) Total ≤ 29 ≥ 30 683 Total 3220 12

Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. We are given 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than 30. Breast Cancer (case) ≤ 29 2537 ≥ 30 683 Total 3220 No Breast Cancer (Controls) Total 12

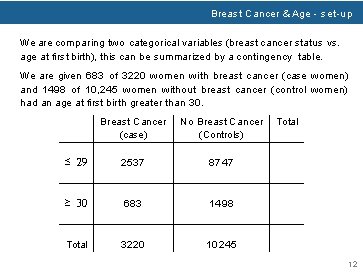
Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. We are given 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than 30. Breast Cancer (case) No Breast Cancer (Controls) ≤ 29 2537 ≥ 30 683 1498 Total 3220 10245 Total 12

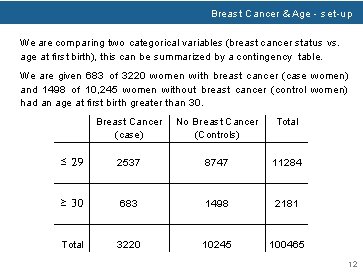
Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. We are given 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than 30. Breast Cancer (case) No Breast Cancer (Controls) ≤ 29 2537 8747 ≥ 30 683 1498 Total 3220 10245 Total 12

Breast Cancer & Age - set-up We are comparing two categorical variables (breast cancer status vs. age at first birth), this can be summarized by a contingency table. We are given 683 of 3220 women with breast cancer (case women) and 1498 of 10, 245 women without breast cancer (control women) had an age at first birth greater than 30. Breast Cancer (case) No Breast Cancer (Controls) Total ≤ 29 2537 8747 11284 ≥ 30 683 1498 2181 Total 3220 10245 100465 12

Breast Cancer & Age - set-up n case = 3220, nctrl = 10245 ▶ cases: 10

Breast Cancer & Age - set-up n case = 3220, nctrl = 10245 ▶ cases: 100465 women (hospital patients) with at least one child ▶ variable(s): 10

Breast Cancer & Age - set-up n case = 3220, nctrl = 10245 ▶ cases: 100465 women (hospital patients) with at least one child ▶ variable(s): (1) breast cancer status - categorical, (2) age at first birth - categorical ▶ parameter of interest: 10

Breast Cancer & Age - set-up n case = 3220, nctrl = 10245 ▶ cases: 100465 women (hospital patients) with at least one child ▶ variable(s): (1) breast cancer status - categorical, (2) age at first birth - categorical ▶ parameter of interest: p case − pctrl – Note: p c a s e = P( age ≥ 30 |case) and p c a s e = P( age ≥ 30 |ctrl) 10

Breast Cancer & Age - set-up n case = 3220, nctrl = 10245 ▶ cases: 100465 women (hospital patients) with at least one child ▶ variable(s): (1) breast cancer status - categorical, (2) age at first birth - categorical ▶ parameter of interest: p case − pctrl – Note: p c a s e = P( age ≥ 30 |case) and p c a s e = P( age ≥ 30 |ctrl) ▶ test: compare two population proportion of independent groups ▶ hypotheses: 10

Breast Cancer & Age - set-up n case = 3220, nctrl = 10245 ▶ cases: 100465 women (hospital patients) with at least one child ▶ variable(s): (1) breast cancer status - categorical, (2) age at first birth - categorical ▶ parameter of interest: p case − pctrl – Note: p c a s e = P( age ≥ 30 |case) and p c a s e = P( age ≥ 30 |ctrl) ▶ test: compare two population proportion of independent groups ▶ hypotheses (two tailed): Ho: p case − pctrl = 0 Ha: p case − pctrl ≠ 0 10

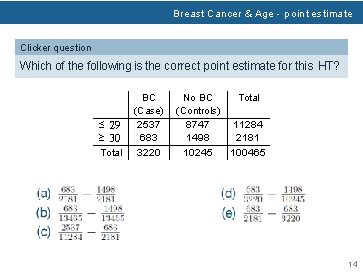
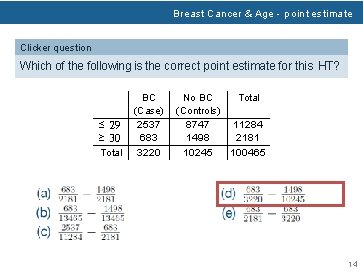
Breast Cancer & Age - point estimate Clicker question Which of the following is the correct point estimate for this HT? ≤ 29 ≥ 30 Total BC (Case) 2537 683 3220 No BC Total (Controls) 8747 11284 1498 2181 10245 100465 14

Breast Cancer & Age - point estimate Clicker question Which of the following is the correct point estimate for this HT? ≤ 29 ≥ 30 Total BC (Case) 2537 683 3220 No BC Total (Controls) 8747 11284 1498 2181 10245 100465 14

Breast Cancer & Age - standard error Clicker question Which of the following is the correct standard error for this HT? ≤ 29 ≥ 30 Total p BC (Case) 2537 683 3220 0. 212 No BC Total (Controls) 8747 11284 1498 2181 10245 100465 0. 146 0. 162 15

Breast Cancer & Age - standard error Clicker question Which of the following is the correct standard error for this HT? ≤ 29 ≥ 30 Total p BC (Case) 2537 683 3220 0. 212 No BC Total (Controls) 8747 11284 1498 2181 10245 100465 0. 146 0. 162 Must use: Pooled Proportion = (#successes)/(total) *Would we calculate the standard error the same way if we were doing a confidence interval? 15

Breast Cancer & Age - standard error Clicker question Which of the following is the correct standard error for this HT? ≤ 29 ≥ 30 Total p BC (Case) 2537 683 3220 0. 212 No BC Total (Controls) 8747 11284 1498 2181 10245 100465 0. 146 0. 162 Must use: Pooled Proportion = (#successes)/(total) *Would we calculate the standard error the same way if we were doing a confidence interval? NO 15

Breast Cancer & Age - test statistic & p-value Original Question: How can we assess whether this difference is significant or simply due to chance? Conclusion: Reject the null hypothesis. There exists sufficient evidence to suggest that there is a statistically significant difference in the proportion of women who have their first child at age at 30 or older in those that do and do not have breast cancer. 16

Breast Cancer & Age - test statistic & p-value What else can we conclude with this same result? (Hint: Think about independence). 16

Breast Cancer & Age - test statistic & p-value What else can we conclude with this same result? (Hint: Think about independence). Conclusion: Reject the null hypothesis. There exists sufficient evidence to suggest that age of first birth in women (≥ 30/<30) and getting breast cancer are dependent. 16

Breast Cancer & Age - confidence interval ▶ Confidence level: 98% 17

Breast Cancer & Age - confidence interval ▶ Confidence level: 98% ▶ Theoretical: Using a critical value based on the Z distr. (z⋆): point estimate ± ME = point estimate ± z⋆× SE 17

Breast Cancer & Age - confidence interval ▶ Confidence level: 98% ▶ Theoretical: Using a critical value based on the Z distr. (z⋆): point estimate ± ME = point estimate ± z⋆× SE 17

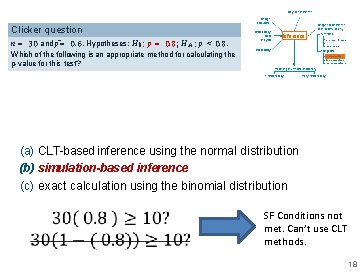
Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Which of the following is an appropriate method for calculating the p-value for this test? Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) CLT-based inference using the normal distribution (b) simulation-based inference (c) exact calculation using the binomial distribution 18

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Which of the following is an appropriate method for calculating the p-value for this test? Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) CLT-based inference using the normal distribution (b) simulation-based inference (c) exact calculation using the binomial distribution 18

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Which of the following is an appropriate method for calculating the p-value for this test? Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) CLT-based inference using the normal distribution (b) simulation-based inference (c) exact calculation using the binomial distribution 18

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Which of the following is an appropriate method for calculating the p-value for this test? Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) CLT-based inference using the normal distribution (b) simulation-based inference (c) exact calculation using the binomial distribution SF Conditions not met. Can’t use CLT methods. 18

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Suppose we wanted to use simulation-based methods. Which of the following is the correct set up for this hypothesis test? Red: success, blue: failure, pˆsim = proportion of reds in simulated samples. Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Place 60 red and 40 blue chips in a bag. Sample, with replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 8. (b) Place 80 red and 20 blue chips in a bag. Sample, without replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (c) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (d) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 100 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. 19

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Suppose we wanted to use simulation-based methods. Which of the following is the correct set up for this hypothesis test? Red: success, blue: failure, pˆsim = proportion of reds in simulated samples. Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Place 60 red and 40 blue chips in a bag. Sample, with replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 8. (b) Place 80 red and 20 blue chips in a bag. Sample, without replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (c) Place 80 red and 20 blue chips in a bag. Sample, w ith replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (d) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 100 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. 19

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Suppose we wanted to use simulation-based methods. Which of the following is the correct set up for this hypothesis test? Red: success, blue: failure, pˆsim = proportion of reds in simulated samples. Design ofstudies Exploratory data analysis Inference Frequentist inference (CLT & simulation) numerical one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory Place 80 red and 20 blue chips in a bag. Sample, w ith replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. Ultimate Goal: 1. Generate a simulated distribution that assumes H 0 : p = 0. 8 is true (or is centered at 0. 8) 2. P-value= P(pˆ ≤ 0. 6| H 0 : p = 0. 8 is true) 19

Bayesian inference *The probability of n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. picking. Inference a success Suppose we wanted to use simulation-based methods. Which of the following is the correct set up for this hypothesis test? Red: (red) must be = to the success, blue: failure, pˆsim = proportion of reds in simulated samples. null value 0. 8 (=80 red/100 total). 30 (a) Place 60 red and 40 blue chips in a bag. Sample, with replacement, Clicker question Design ofstudies Frequentist inference (CLT & simulation) numerical Exploratory data analysis one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 8. (b) Place 80 red and 20 blue chips in a bag. Sample, without replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (c) Place 80 red and 20 blue chips in a bag. Sample, w ith replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (d) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 100 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. 19

Bayesian inference Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Suppose we wanted to use simulation-based methods. Which of the following is the correct set up for this hypothesis test? Red: success, blue: failure, pˆsim = proportion of reds in simulated samples. Design ofstudies *Each trial must be Inference selected with replacement. Frequentist inference (CLT & simulation) numerical Exploratory data analysis one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory (a) Place 60 red and 40 blue chips in a bag. Sample, with replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 8. (b) Place 80 red and 20 blue chips in a bag. Sample, without replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (c) Place 80 red and 20 blue chips in a bag. Sample, w ith replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (d) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 100 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. 19

*The sample size (n) for each simulation n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Inference Suppose we wanted to use simulation-based methods. Which of proportion must match the following is the correct set up for this hypothesis test? Red: the sample size (n) for success, blue: failure, pˆsim = proportion of reds in simulated samples. the original sample proportion. (a) Place 60 red and 40 blue chips in a bag. Sample, with replacement, 30 Bayesian inference Clicker question Design ofstudies Frequentist inference (CLT & simulation) numerical Exploratory data analysis one mean & median many means Probability categorical one proportion two proportions many proportions Modeling (numerical response) 1 explanatory many explanatory chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 8. (b) Place 80 red and 20 blue chips in a bag. Sample, without replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (c) Place 80 red and 20 blue chips in a bag. Sample, w ith replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (d) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 100 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. 19

Clicker question n = 30 and pˆ= 0. 6. Hypotheses: H 0 : p = 0. 8; H A : p < 0. 8. Suppose we wanted to use simulation-based methods. Which of the following is the correct set up for this hypothesis test? Red: success, blue: failure, pˆsim = proportion of reds in simulated samples. (a) Place 60 red and 40 blue chips in a bag. Sample, with replacement, 30 *In this tailed): chips andexample calculate the(left proportion of reds. Repeat this many times and calculate the. P(pˆ proportion of simulations 0. 8. true) P-value= ≤ 0. 6| H p =pˆsim 0. 8≤ is 0 : where sim (b) Place 80 red and 20 blue chips in a bag. Sample, without replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (c) Place 80 red and 20 blue chips in a bag. Sample, w ith replacement, 30 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. (d) Place 80 red and 20 blue chips in a bag. Sample, with replacement, 100 chips and calculate the proportion of reds. Repeat this many times and calculate the proportion of simulations where pˆsim ≤ 0. 6. 19

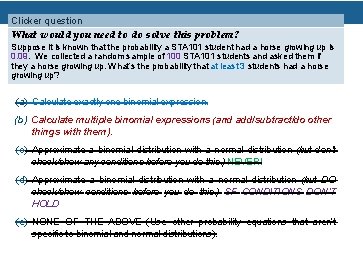
Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had a horse growing up. What’s the probability that at least 3 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had a horse growing up. What’s the probability that at least 3 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had a horse growing up. What’s the probability that at least 3 students had a horse growing up? Calculate multiple binomial expressions (and add/subtract/do other things with them). Binomial distribution is needed because: a) n=100 trials (and asking for the probability of exactly/at least/at most k=3 of these trials are a success=horse) b) each trial has probability 0. 09 c) independent trials d) only two possibilities (horse/no horse)

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they a horse growing up. What’s the probability that at least 3 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) NEVER! (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) SF CONDITIONS DON’T HOLD (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that at least 3 students had a horse growing up? Calculate multiple binomial expressions (and add/subtract/do other things with them).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that at least 3 students had a horse growing up? Calculate multiple binomial expressions (and add/subtract/do other things with them).

Clicker question Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had at least one horse growing up. Describe the shape of this distribution. (a) Unimodal and symmetric (b) Skewed to the right (c) Skewed to the left (d) Uniform

Clicker question Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had at least one horse growing up. Describe the shape of this distribution. (a) Unimodal and symmetric (SF conditions don’t hold… so it can’t be this) (b) Skewed to the right (peak of distribution will be at 0. 09… close to 0… rest of the distribution will slowly taper down as you go to the right towards 1) (c) Skewed to the left (d) Uniform

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that 3 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 100 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that 3 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09 and the probability that they had a dog is 0. 62 and the probability that they had a dog and a horse is 0. 05. What is the probability a student had a dog or a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09 and the probability that they had a dog is 0. 62 and the probability that they had a dog and a horse is 0. 05. What is the probability a student had a dog or a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 200 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that at least 50 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 200 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that at least 50 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). Doing it this way without a computer (advanced calculator would take a really long time). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions). SF Conditions Hold: • 200(. 09)≥ 10 • 200(1 -. 09)≥ 10

Clicker question What would you need to do solve this problem? Suppose it is known that the probability a STA 101 student had a horse growing up is 0. 09. We collected a random sample of 200 STA 101 students and asked them if they had at least one horse growing up. What’s the probability that at least 50 students had a horse growing up? (a) Calculate exactly one binomial expression. (b) Calculate multiple binomial expressions (and add/subtract/do other things with them). Doing it this way without a computer (advanced calculator would take a really long time). (c) Approximate a binomial distribution with a normal distribution (but don’t check/show any conditions before you do this. ) (d) Approximate a binomial distribution with a normal distribution (but DO check/show conditions before you do this. ) (e) NONE OF THE ABOVE (Use other probability equations that aren’t specific to binomial and normal distributions).

Clicker question Describe the sampling method used (and if there is bias). We want to know what STA 101 students favorite subject in high school was. Group everyone in the class today by major. Then randomly sample 3 students from each major and ask them their favorite. (a) Simple random sample (b) Stratified sampling (c) Cluster sampling (d) Multistage sampling (e) Sampling with a non-response bias

Clicker question Describe the sampling method used (and if there is bias). We want to know what STA 101 students favorite subject in high school was. Group everyone in the class by major. Then randomly sample 3 students from each major. Collect their responses today in class. (a) Simple random sample (b) Stratified sampling (c) Cluster sampling (d) Multistage sampling (e) Sampling with a non-response bias

Clicker question Describe the sampling method used (and if there is bias). We want to know what STA 101 students favorite subject in high school was. Randomly select 7 groups in this class and randomly ask two students in each chosen group. Make sure that every student eventually responds. (a) Simple random sample (b) Stratified sampling (c) Cluster sampling (d) Multistage sampling (e) Sampling with a non-response bias

Clicker question Describe the sampling method used (and if there is bias). We want to know what STA 101 students favorite subject in high school was. Randomly select 7 groups in this class and randomly ask two students in each chosen group. Make sure that every student eventually responds. (a) Simple random sample (b) Stratified sampling (c) Cluster sampling (d) Multistage sampling (e) Sampling with a non-response bias

Clicker question We just conducted an ANOVA test comparing 4 means with a total sample size of n=100. The ANOVA hypothesis was found to be statistically significant at α=0. 05. Which of the following are the appropriate p-value and significance level to use for a post-hoc pairwise comparison test?

Clicker question We just conducted an ANOVA test comparing 4 means with a total sample size of n=100. The ANOVA hypothesis was found to be statistically significant at α=0. 05. Which of the following are the appropriate p-value and significance level to use for a post-hoc pairwise comparison test?

Clicker question (a) (b) (c) (d) STATEMENT 1 is TRUE and STATEMENT 2 is FALSE STATEMENT 2 is TRUE and STATEMENT 1 is FALSE STATEMENT 1 and 2 are BOTH TRUE STATEMENT 1 and 2 are BOTH FALSE

Clicker question (a) (b) (c) (d) STATEMENT 1 is TRUE and STATEMENT 2 is FALSE STATEMENT 2 is TRUE and STATEMENT 1 is FALSE STATEMENT 1 and 2 are BOTH TRUE STATEMENT 1 and 2 are BOTH FALSE

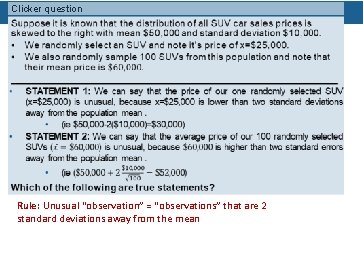
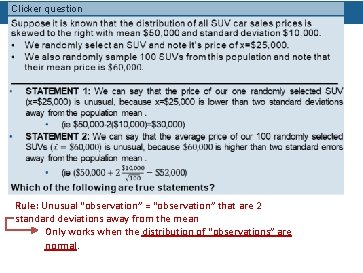
Clicker question Rule: Unusual “observation” = “observations” that are 2 standard deviations away from the mean

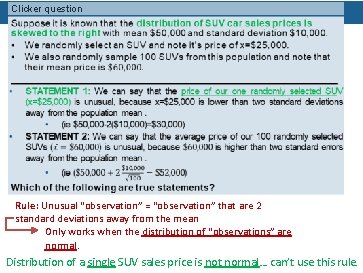
Clicker question Rule: Unusual “observation” = “observation” that are 2 standard deviations away from the mean Only works when the distribution of “observations” are normal.

Clicker question Rule: Unusual “observation” = “observation” that are 2 standard deviations away from the mean Only works when the distribution of “observations” are normal. Distribution of a single SUV sales price is not normal… can’t use this rule.

Clicker question Rule: Unusual “observation” = “observation” that are 2 standard deviations away from the mean Only works when the distribution of “observations” are normal. Distribution of sample SUV means (sample size 100) IS normal because n >30 (and random sampling is used and n=100<10% of all SUVs)… CAN use this rule!

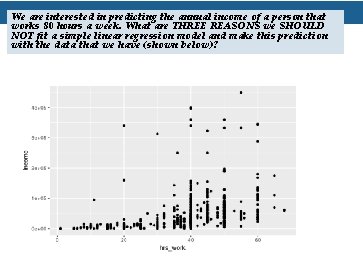
We are interested in predicting the annual income of a person that works 80 hours a week. What are THREE REASONS we SHOULD NOT fit a simple linear regression model and make this prediction with the data that we have (shown below)?

We are interested in predicting the annual income of a person that works 80 hours a week. What are THREE REASONS we SHOULD NOT fit a simple linear regression model and make this prediction with the data that we have (shown below)? 1. Condition Violation: The relationship is nonlinear. 2. Condition Violation: The variance of the residuals (when fitting a linear model) would increase as hours worked increases…. so non -homoscedastic residuals. 3. Extrapolation: 80 hrs/week working is outside the range of data (highest our data goes is 65 hrs/week). So our prediction would be an unreliable extrapolation.

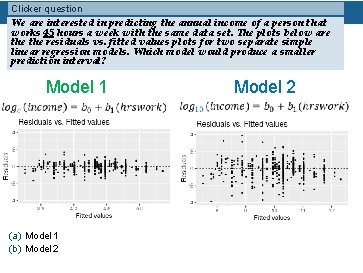
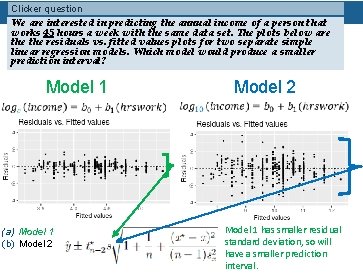
Clicker question We are interested in predicting the annual income of a person that works 45 hours a week with the same data set. The plots below are the residuals vs. fitted values plots for two separate simple linear regression models. Which model would produce a smaller prediction interval? Model 1 (a) Model 1 (b) Model 2

Clicker question We are interested in predicting the annual income of a person that works 45 hours a week with the same data set. The plots below are the residuals vs. fitted values plots for two separate simple linear regression models. Which model would produce a smaller prediction interval? Model 1 (a) Model 1 (b) Model 2 Model 1 has smaller residual standard deviation, so will have a smaller prediction interval.

Clicker question A recent housing survey was conducted to determine the price of a typical home in Glendale, CA. Glendale is mostly middle-class, with one very expensive suburb. The mean price of a house was roughly $650, 000. Which of the following statements is most likely to be true? (a) Most houses in Glendale cost more than $650, 000. (b) Most houses in Glendale cost less than $650, 000. (c) There about as many houses in Glendale that cost more than $650, 000 than less than this amount. (d) We need to know the standard deviation to answer this question

Clicker question A recent housing survey was conducted to determine the price of a typical home in Glendale, CA. Glendale is mostly middle-class, with one very expensive suburb. The mean price of a house was roughly $650, 000. Which of the following statements is most likely to be true? (a) Most houses in Glendale cost more than $650, 000. (b) Most houses in Glendale cost less than $650, 000. (c) There about as many houses in Glendale that cost more than $650, 000 than less than this amount. (d) We need to know the standard deviation to answer this question

Clicker question (a) Z-test (b) T-test (c) Randomization testing (d) Bootstrap testing

Clicker question (a) Z-test (b) T-test (c) Randomization testing (d) Bootstrap testing