Unit 7 Entropia e disordine Copyright 2009 Zanichelli

Unità 7 Entropia e disordine Copyright © 2009 Zanichelli editore

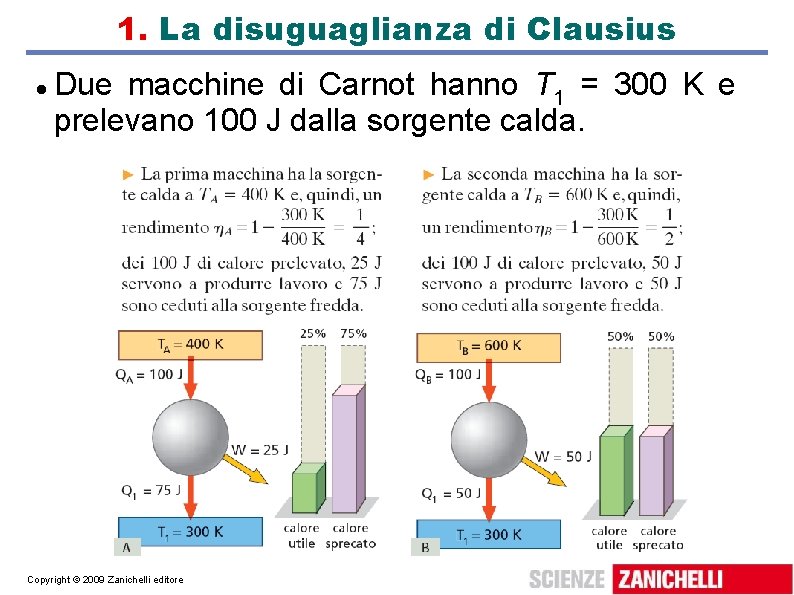
1. La disuguaglianza di Clausius Due macchine di Carnot hanno T 1 = 300 K e prelevano 100 J dalla sorgente calda. Copyright © 2009 Zanichelli editore

La disuguaglianza di Clausius Gli stessi 100 J assorbiti producono più lavoro se provengono da una sorgente a temperatura più alta; il calore a bassa temperatura è energia in transito, ma è energia degradata. Per capire il comportamento del calore alle diverse temperature, Clausius introdusse il concetto di entropia; enunciamo la disuguaglianza di Clausius per definire l'entropia. Copyright © 2009 Zanichelli editore

La disuguaglianza di Clausius Disuguaglianza di Clausius: la sommatoria, su tutto un ciclo, dei rapporti tra i calori scambiati e le temperature a cui avviene lo scambio è sempre minore o uguale a zero. Vale l'uguaglianza se e solo se la macchina è reversibile. Copyright © 2009 Zanichelli editore

Il simbolo di sommatoria La disuguaglianza si può scrivere utilizzando il simbolo di sommatoria: e Il simbolo da 1 a n”. Esempio: se Copyright © 2009 Zanichelli editore significa “sommatoria per i che va è

Dimostrazione della disuguaglianza di Clausius Data una macchina che lavora tra T 1 e T 2: per il Teorema di Carnot è < R, (vale “=” se e solo se la macchina è reversibile); per definizione è: = 1 – |Q |/Q ; 1 2 R = 1 – T 1/T 2; sostituendo: Copyright © 2009 Zanichelli editore , ovvero

Dimostrazione della disuguaglianza di Clausius nella disuguaglianza: poiché Q 1 è negativo, |Q 1| = –Q 1 : (n = 2) , Se la macchina è reversibile, = R, quindi (uguaglianza di Clausius per n = 2) Copyright © 2009 Zanichelli editore

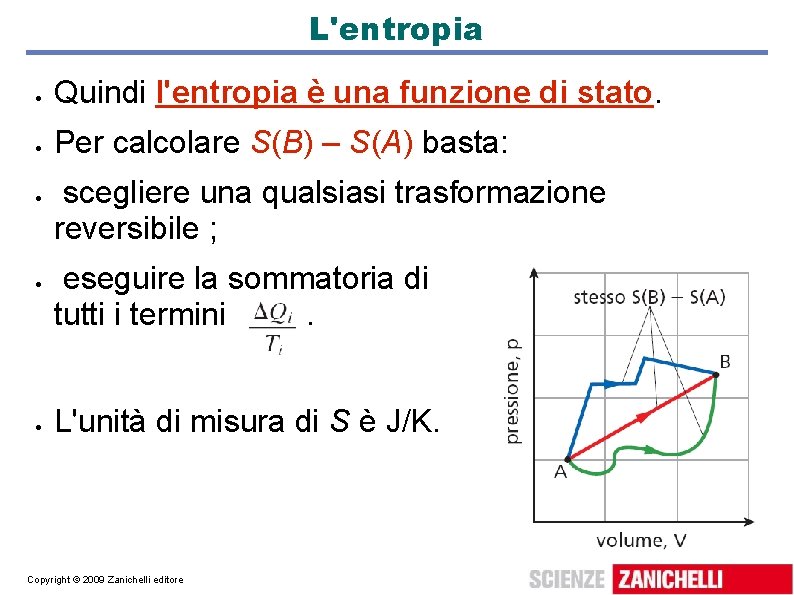
2. L'entropia Definiamo variazione di entropia di un sistema che passa dallo stato A allo stato B: la sommatoria è su tutti gli scambi di calore che fanno passare da A a B con una trasformazione reversibile. Si dimostra che S(B) – S(A) non dipende dalla trasformazione, ma solo da A e B. Copyright © 2009 Zanichelli editore

L'entropia Quindi l'entropia è una funzione di stato. Per calcolare S(B) – S(A) basta: scegliere una qualsiasi trasformazione reversibile ; eseguire la sommatoria di tutti i termini. L'unità di misura di S è J/K. Copyright © 2009 Zanichelli editore

Definizione di entropia Per definire l'entropia si parte da S(B) – S(A): l'entropia S, così come l'energia potenziale, è definita a partire da un livello di zero arbitrario: se R è lo stato per cui S(R) = 0, per ogni stato C: Si può scegliere come stato R quello di un cristallo perfetto di atomi identici a T = 0 K. L'entropia è una grandezza estensiva. Copyright © 2009 Zanichelli editore

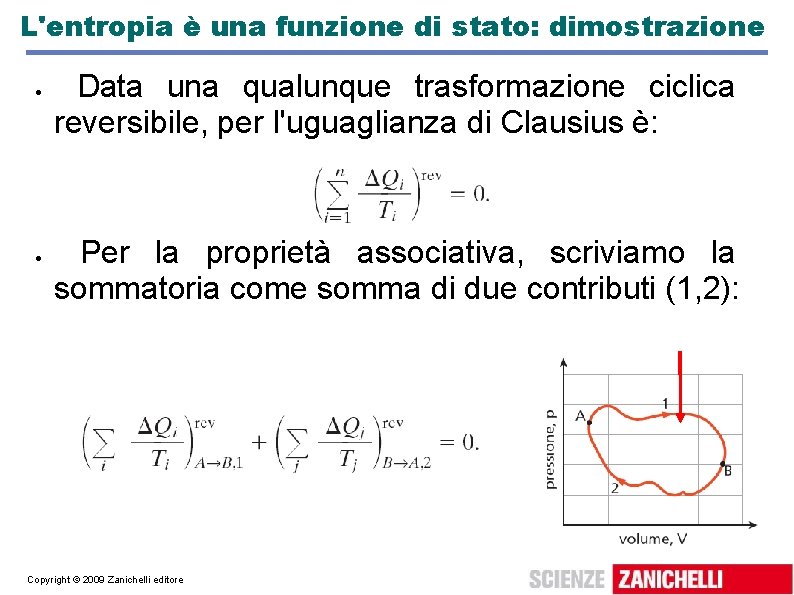
L'entropia è una funzione di stato: dimostrazione Data una qualunque trasformazione ciclica reversibile, per l'uguaglianza di Clausius è: Per la proprietà associativa, scriviamo la sommatoria come somma di due contributi (1, 2): Copyright © 2009 Zanichelli editore

L'entropia è una funzione di stato: dimostrazione Portando il secondo termine a destra: ovvero Sono gli scambi di calore che permettono di andare lungo il percorso 2 in senso inverso, cioè da A a B. La quantità non dipende dal percorso. Copyright © 2009 Zanichelli editore

3. L'entropia di un sistema isolato Un sistema chiuso e isolato non scambia materia né energia con l'ambiente esterno. Consideriamo diviso in due sottosistemi: = 1 + 2. 1: cilindro con pistone a tenuta; 2: laboratorio con sorgenti di calore Copyright © 2009 Zanichelli editore

Le trasformazioni reversibili non variano l'entropia di un sistema isolato In un sistema isolato dove hanno luogo solo trasformazioni reversibili l'entropia rimane costante. In una trasformazione reversibile, riceve da le quantità di calore Q 1, Q 2, . . . , Qn alle rispettive temperature T 1, T 2, . . . , Tn. La variazione totale dell'entropia di è la somma delle due variazioni, quella di e quella di . Copyright © 2009 Zanichelli editore

Le trasformazioni reversibili non variano l'entropia di un sistema isolato La variazione di entropia di è: mentre quella di è: Pertanto la variazione di entropia totale è: S = S 1(B) – S 1(A) + S 2(B) – S 2(A) = 0. Copyright © 2009 Zanichelli editore

Le trasformazioni irreversibili aumentano l'entropia di un sistema isolato In un sistema isolato dove hanno luogo trasformazioni irreversibili l'entropia aumenta. Sia: l'interno di una macchina di Joule a temperatura T; l'esterno della macchina, compresa la Terra. compie lavoro W su , la cui entropia aumenta di S = W/T; l'entropia di è invariata (non ha avuto scambi di calore). Copyright © 2009 Zanichelli editore

L'entropia dell'Universo Per quanto visto finora: ogni trasformazione che avviene in un sistema isolato provoca una variazione di entropia S > 0 (= 0 se e solo se la trasformazione è reversibile); l'Universo è tutto ciò che esiste: non c'è un ambiente “esterno” con cui scambiare energia; in esso avvengono continuamente trasformazioni irreversibili, quindi l'entropia dell'Universo è in aumento incessante. Copyright © 2009 Zanichelli editore

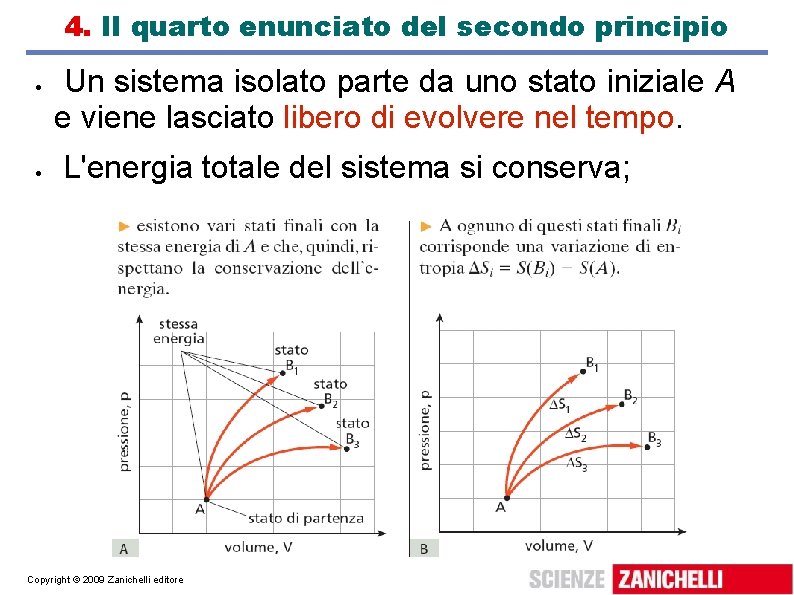
4. Il quarto enunciato del secondo principio Un sistema isolato parte da uno stato iniziale A e viene lasciato libero di evolvere nel tempo. L'energia totale del sistema si conserva; Copyright © 2009 Zanichelli editore

Il quarto enunciato del secondo principio Dallo stato A allo stato B la variazione di entropia sarà sempre S > 0. Quarto enunciato del Secondo principio della termodinamica: l'evoluzione spontanea di un sistema isolato giunge ad uno stato di equilibrio a cui corrisponde il massimo aumento dell'entropia (compatibilmente con il primo principio della termodinamica). Copyright © 2009 Zanichelli editore

5. L'entropia di un sistema non isolato In un sistema non isolato l'entropia può diminuire (ad es. nell'interno di un frigo); la diminuzione può avvenire solo a spese dell'energia fornita da un sistema . Nel caso del frigorifero, è formato dal motore, dal sistema elettrico, dalle serpentine e dal fluido. Copyright © 2009 Zanichelli editore

L'entropia di un sistema non isolato Caso ideale: frigorifero reversibile. STOT= 0. Copyright © 2009 Zanichelli editore

L'entropia di un sistema non isolato Caso reale: frigorifero irreversibile. L'aumento di entropia in è maggiore del modulo della diminuzione in : STOT>0. Anche se in un sistema si ha S<0, nel resto dell'Universo si ha un aumento di entropia maggiore di | S|. Copyright © 2009 Zanichelli editore

6. Il secondo principio dal punto di vista molecolare I sistemi reali evolvono spontaneamente con la tendenza alla crescita dell'entropia. Studiamo il fenomeno a livello microscopico: un disco di massa m e velocità v è in una scatola con gas perfetto; gli urti con le pareti sono elastici; non vi è attrito; la scatola è isolata dall'esterno. Copyright © 2009 Zanichelli editore

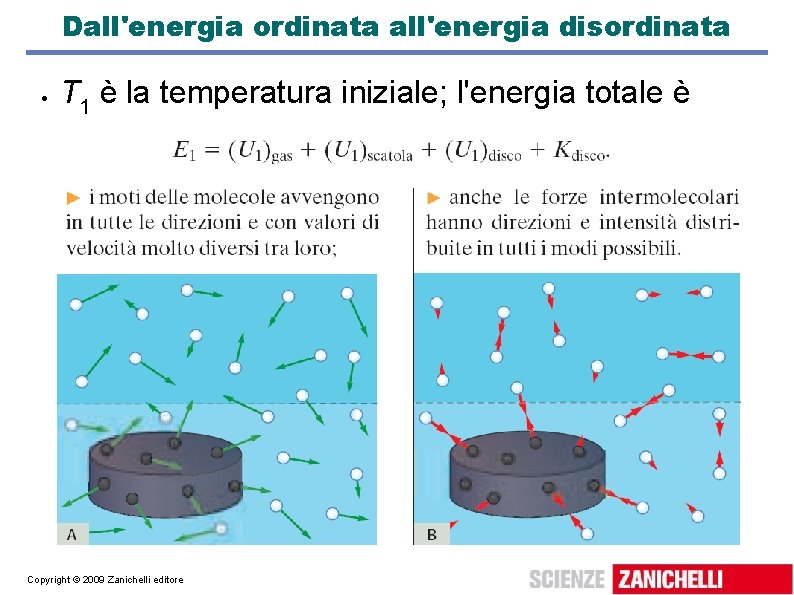
Dall'energia ordinata all'energia disordinata T 1 è la temperatura iniziale; l'energia totale è Copyright © 2009 Zanichelli editore

Dall'energia ordinata all'energia disordinata Le energie interne U sono disordinate, perché i moti delle molecole e le forze hanno tutte le possibili direzioni e intensità; l'energia cinetica del disco, K, è ordinata, perché tutte le molecole del disco devono muoversi con la stessa velocità v (oltre alla velocità di agitazione termica). Copyright © 2009 Zanichelli editore

Dall'energia ordinata all'energia disordinata Dopo un certo tempo e moltissimi urti elastici con le pareti, il disco si ferma: ha trasferito tutta l'energia cinetica alle molecole del gas; la temperatura del sistema (disco+gas+scatola) è aumentata; l'energia totale del sistema è E 2 = E 1, con: Tutta l'energia ordinata si è trasformata spontaneamente in energia disordinata. Copyright © 2009 Zanichelli editore

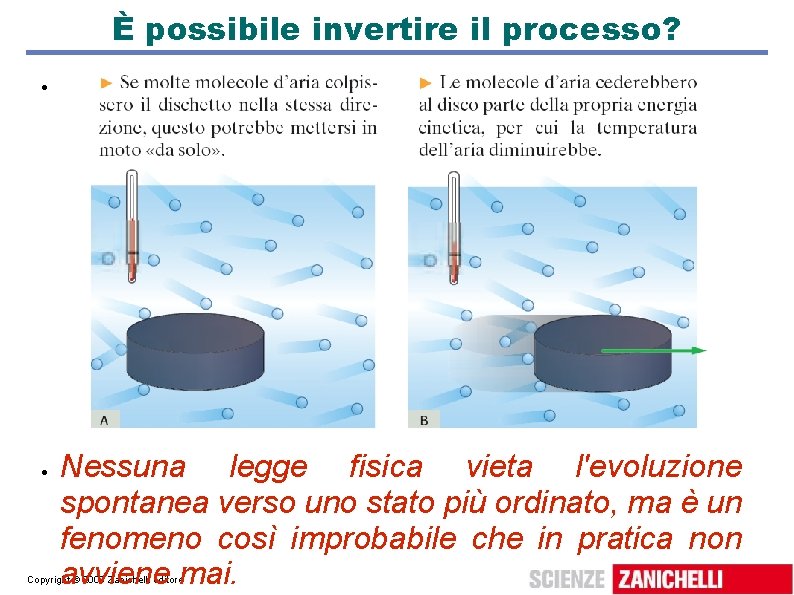
È possibile invertire il processo? Nessuna legge fisica vieta l'evoluzione spontanea verso uno stato più ordinato, ma è un fenomeno così improbabile che in pratica non avviene mai. Copyright © 2009 Zanichelli editore

Interpretazione microscopica del secondo principio La probabilità che le molecole di un gas a temperatura ambiente (1019 in un cm 3) colpiscano il disco nella stessa direzione è circa zero; se il disco si mettesse in moto solo a spese della U interna, l'enunciato di Kelvin sarebbe violato: si sarebbe prodotto W con una sola sorgente; il secondo principio è in accordo con l'esperienza perché i fenomeni che lo violano sono così improbabili da non avvenire mai. Copyright © 2009 Zanichelli editore

7. Stati macroscopici e stati microscopici Stato macroscopico o macrostato di un sistema fisico: insieme dei valori delle variabili macroscopiche permettono di identificarne le proprietà (per un gas perfetto: p, V, T, n); Stato microscopico o microstato di un sistema fisico: precisa configurazione dei suoi costituenti microscopici (per un gas: masse, posizioni, velocità di tutte le molecole). Copyright © 2009 Zanichelli editore

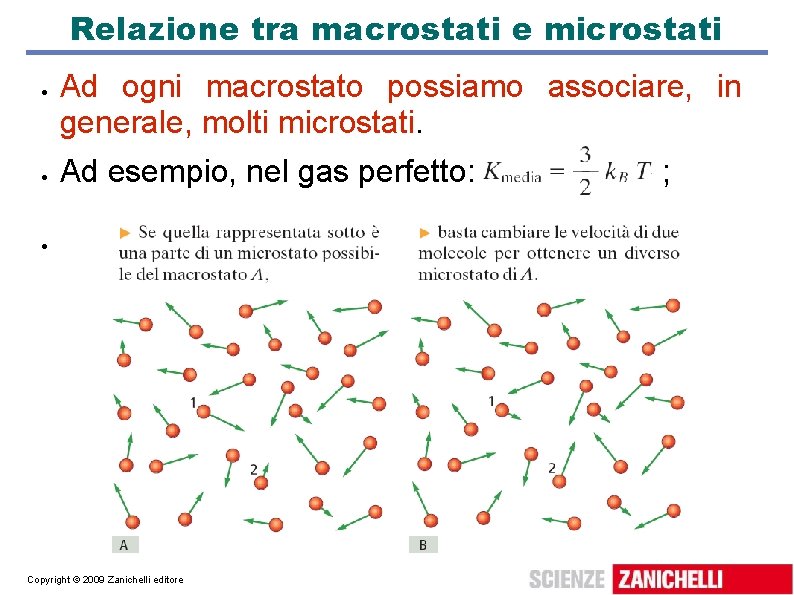
Relazione tra microstati e macrostati Ad ogni microstato possiamo associare uno e un solo macrostato, le cui proprietà sono definite dai valori medi o totali delle grandezze intensive o estensive che lo caratterizzano. Per un gas perfetto le grandezze dipendono da: p: dalla forza media esercitata dalle molecole sulle pareti; V: dalla zona complessiva di spazio disponibile; T: dall'energia cinetica media delle molecole; m: somma delle masse di tutte le molecole. Copyright © 2009 Zanichelli editore

Relazione tra macrostati e microstati Ad ogni macrostato possiamo associare, in generale, molti microstati. Ad esempio, nel gas perfetto: Copyright © 2009 Zanichelli editore ;

La molteplicità di un macrostato Si definisce molteplicità del macrostato A, W(A), il numero di microstati diversi che corrispondono ad A. Esempio: molteplicità dei macrostati di 8 molecole di gas nelle due metà (destra e sinistra) di un recipiente. Copyright © 2009 Zanichelli editore

La molteplicità di un macrostato Il macrostato con tutte le 8 molecole da un lato è estremamente improbabile (1/128). Quindi è praticamente impossibile tornare allo stato “più ordinato” con 1023 molecole! L'inchiostro diffonde nell'acqua: è del tutto improbabile che torni ad occupare il volume Copyright © 2009 Zanichelli editore

Microstati ordinati e disordinati Consideriamo più ordinati i microstati in cui si ha minima indeterminazione sulla posizione delle particelle. (Ad esempio, sapere che tutte le molecole sono nella metà di un recipiente dimezza l'incertezza su ciascuna posizione). Abbiamo verificato che più un microstato è disordinato, maggiore è la probabilità con la quale esso può verificarsi spontaneamente. Copyright © 2009 Zanichelli editore

8. L'equazione di Boltzmann per l'entropia L. Boltzmann dimostrò che l'entropia di un macrostato dipende dalla sua molteplicità: k. B = 1, 38 x 10 -23 J/K ln: logaritmo in base e (e 2, 72) Lo zero di S corrisponde ad un cristallo perfetto a T = 0 K, con tutti gli atomi fermi e W(A) = 1 (ln 1 = 0). Copyright © 2009 Zanichelli editore

L'equazione di Boltzmann per l'entropia L'entropia è una grandezza estensiva: infatti per due sottosistemi A e B si ha: e La molteplicità del sistema composto da A e B è e l'entropia di A B è proprietà dei logaritmi Copyright © 2009 Zanichelli editore grandezza estensiva

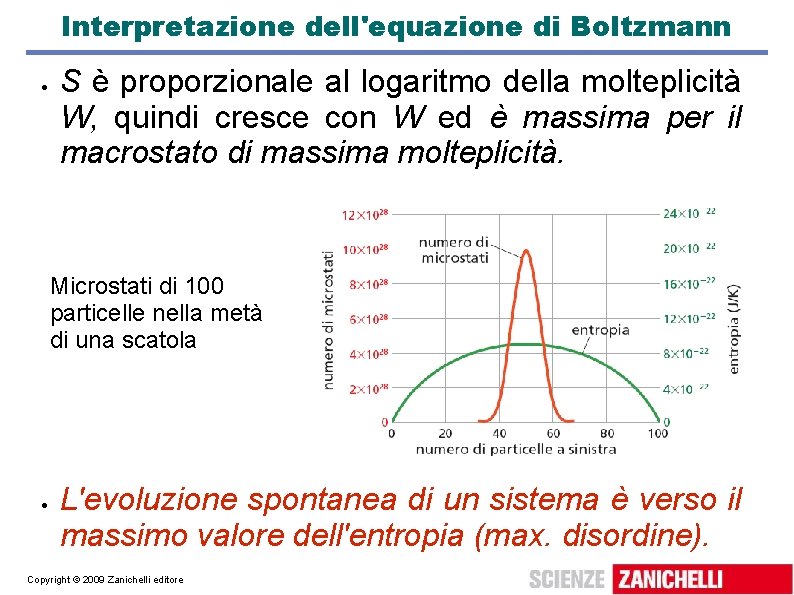
Interpretazione dell'equazione di Boltzmann S è proporzionale al logaritmo della molteplicità W, quindi cresce con W ed è massima per il macrostato di massima molteplicità. Microstati di 100 particelle nella metà di una scatola L'evoluzione spontanea di un sistema è verso il massimo valore dell'entropia (max. disordine). Copyright © 2009 Zanichelli editore

9. Il terzo principio della termodinamica Negli ultimi due secoli si sono ottenute in laboratorio temperature sempre più basse: nel 1834 Thilorier raggiunge 163 K (CO 2 solida); nel 1898 Dewar liquefà l'ossigeno a 23 K; nel 1908 Onnes liquefà l'elio a 5 K; nel 1960 si raggiungono i 10 -6 K; nel 1995 il condensato di Bose-Einstein arriva a 0, 17 x 10 -6 K; nel 2003 si raggiungono sperimentalmente i 4, 5 x 10 -10 K. Copyright © 2009 Zanichelli editore

Il terzo principio della termodinamica Tuttavia, più la temperatura di un corpo si avvicina allo zero assoluto, più è difficile raffreddarlo ulteriormente, secondo il Terzo principio della termodinamica: è impossibile raffreddare un corpo fino allo zero assoluto mediante un numero finito di trasformazioni. (Legge di Nernst) Copyright © 2009 Zanichelli editore

Il terzo principio della termodinamica Riepilogo di tutti i princìpi della termodinamica. Copyright © 2009 Zanichelli editore