Unit 61 Engineering Thermodynamics Lesson 7 First Law

Unit 61: Engineering Thermodynamics Lesson 7: First Law of Thermodynamics

Objective • The purpose of this lesson is to consider the concepts of work and heat.

First Law of Thermodynamics • The first law is often called the conservation of energy. • In school physics the conservation of energy emphasises changes in kinetic and potential energy and their relationship to work. A more general form of the conservation of energy includes the effects of heat transfer and internal energy – this general form is the first law of thermodynamics.

First Law of Thermodynamics applied to a Cycle • The first law is not derived or proved it is a statement based on experimental observations. • The first law states that for a cycle the net heat transfer is equal to the net work done for a system undergoing a cycle i. e. ΣW = ΣQ or δW = δQ • Note: δ is used because there are inexact differentials • Note the represents integration around a complete cycle

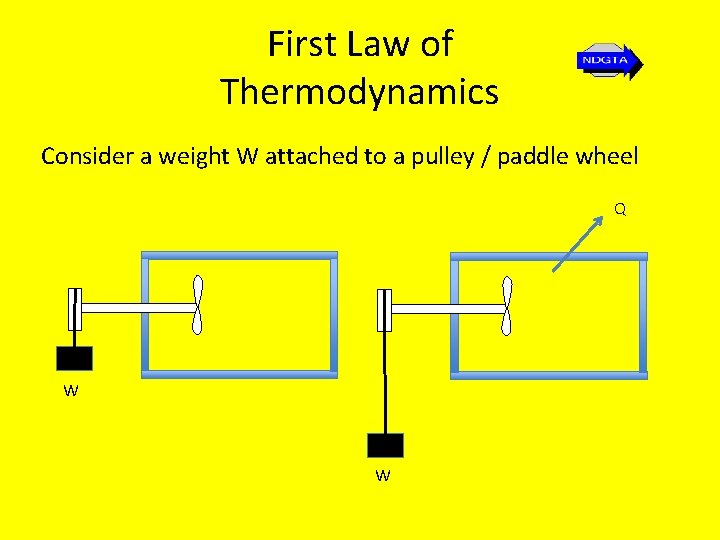
First Law of Thermodynamics Consider a weight W attached to a pulley / paddle wheel Q W W

First Law of Thermodynamics applied to a cycle • Let the weight fall through a certain distance thereby doing work on the system, contained in the insulated tank shown. Work done is weight times distance dropped. • Let the system return to its initial state by transferring heat to the surroundings Q thereby reducing the temperature of the system to its original temperature. • The first law states that this heat transfer will be exactly equal to the work which was done by the falling weight.

First Law of Thermodynamics applied to a Cycle • A spring is stretched a distance of 0. 8 m and attached to a paddle wheel. The paddle wheel then rotates until the spring is un-stretched. Calculate the heat transfer necessary to return the system to its initial state (k = 100 N/m) 0. 8 W 1 -2 = fdx = 100 xdx = 100(0. 82/2) = 32 N. m 0 0 But from first law Q 1 -2 = W 1 -2 = 32 N. m

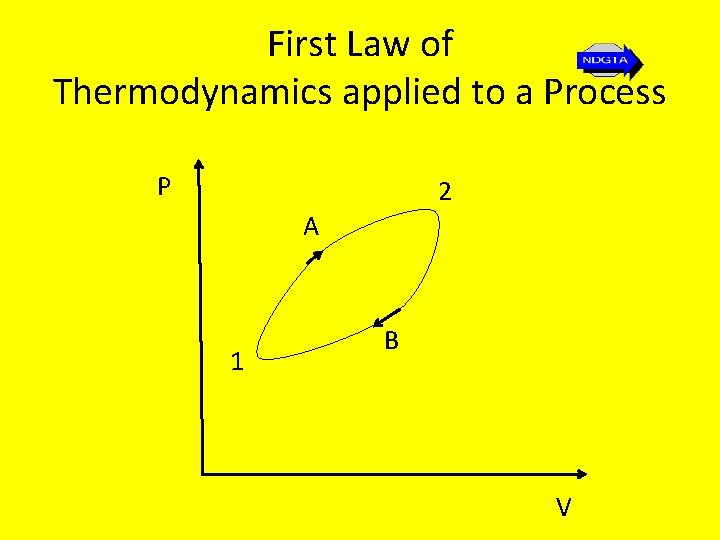
First Law of Thermodynamics applied to a Process • The first law is often applied to a process as the system changes from one state to another. Realising that a cycle results when a system undergoes several processes and returns to the initial state, we could consider a cycle composed of two or more processes represented as shown…

First Law of Thermodynamics applied to a Process P 2 A 1 B V

First Law of Thermodynamics applied to a Cycle δQA + δQB = 1 1 2 δWA + δWB 2 1 2 2 2 δQA - δQB = δWA - δWB 1 1 1 2 2 (δQ – δW)A = (δQ – δW)B 1 1 1

First Law of Thermodynamics applied to a Process • Thus the change in the quantity Q – W from state 1 to state 2 is the same along path A as along path B. • Since this change is independent between states a and 2 we let δQ – δW = d. E (note an exact differential). • E is an extensive property of the system shown experimentally to represent the energy of the system at a particular state. Thus Q 1 -2 – W 1 -2 = E 2 – E 1

First Law of Thermodynamics applied to a Process • Q 1 -2 is the heat transferred to the system during the process from state 1 to state 2. • W 1 -2 is the work done by the system on the surroundings during the process • E 2 and E 1 are the values of the property E. • E represents all the energy – kinetic (KE), potential (PE) and internal (U) (which includes chemical and the energy associated with the atom). Thus Q 1 -2 – W 1 -2 = KE 2 – KE 1 + PE 2 – PE 1 + U 2 – U 1 + Epress

First Law of Thermodynamics applied to a Process • In an open system, the fluid is continuously flowing in and out of the system and work transfers take place. Epress is thus the flow or pressure energy = pressure x volume = PV as the fluid passes through the system • Q 1 -2 – W 1 -2 = KE 2 – KE 1 + PE 2 – PE 1 + (U 2 – U 1) + (Epress 2 – Epress 1) = (m/2)(V 22 –V 12)+ mg(z 2 – z 1) + (U 2 – U 1) + (p 2 V 2 – p 1 V 1)

Enthalpy • In the solution of problems involving systems, certain products or sums or properties occur with regularity. • One combination of properties can be demonstrated by considering the addition of heat to the constant-pressure situation. Consider…

Enthalpy W W Gas Gas Q Heat is added slowly to the system (the gas in the cylinder) which is maintained at constant pressure by assuming a frictionless seal between the piston and the cylinder.

First Law of Thermodynamics applied to a Process • If the KE changes and the potential energy changes of the system are neglected and all other work modes are absent, the first law of thermodynamics requires that… Q – W = U 2 – U 1 • The work done raising the weight for the constant pressure process is given by… W = P(V 2 – V 1) Thus Q = (U + PV)2 - (U + PV)1

Enthalpy • The quantity U + PV is known as enthalpy (H). As this is a combination of properties, it itself is therefore a property. • Specific enthalpy is found by dividing by the mass… h = u + Pv • Thus Q 1 -2 = H 2 – H 1 • Note: the enthalpy was defined using a constantpressure system with the differences between enthalpies between two states being the heat transfer.

Latent Heat • The amount of energy that must be transferred in the form of heat to a substance held at constant pressure in order that a phase change occurs is called latent heat. • It is the change in enthalpy of the substance at the saturated conditions of the two phases • The heat necessary to melt (or freeze) a unit mass of substance at constant pressure is the heat of fusion and is equal to… hif = hf – hi • Where hi is the enthalpy of the saturated solid and hf the enthalpy of the saturated liquid

Latent Heat • The heat of vapourisation is the heat required to completely vapourise a unit mass of saturated liquid (or condense a unit mass of saturated vapour). It is equal to… hfg = hg – hf • When a solid changes phase directly to a gas, sublimation occurs. The heat of sublimation is equal to… hig = hg – hi

Specific Heats • For a simple system only two independent variables are necessary to establish the state of the system. Consequently we can consider the specific internal energy to be a function of temperature and specific volume i. e. u = u(T, v) • Using the chain rule… du = ∂u/∂T|v d. T + ∂u/∂v|Td. V

Specific Heats • Since u, v and T are all properties, the partial derivative is also a property and is called the constant-volume specific heat Cv. Cv = ∂u/∂T|v …this is because for an ideal gas ∂u/∂v|T = 0 Thus du = Cvd. T T 2 i. e u 2 – u 1 = Cvd. T T 1

Specific Heats • For a known Cv(T) this can be integrated to find the change in internal energy over any temperature interval for an ideal gas. • Likewise, considering specific enthalpy to be independent on the two variables T and P i. e. h = h(T, P)we have… dh = ∂h/∂T|pd. T+ ∂h/∂P|T d. P • The constant-pressure specific heat Cp is defined as… Cp = ∂h/∂T|P

Specific Heats • For a known Cv(T) this can be integrated to find the change in internal energy over any temperature interval for an ideal gas. • Likewise, considering specific enthalpy to be independent on the two variables T and P we have… dh = ∂h/∂T|pd. T+ ∂h/∂P|T d. P • Note for an ideal has ∂h/∂P|T = 0 (see next slide) • The constant-pressure specific heat Cp is defined as… Cp = ∂h/∂T|P

Specific Heats • From previous h = u + Pv = u + RT. • Since internal energy u, is only a function of T we see that h is also only a function of T for an ideal gas. Hence for an ideal gas… ∂h/∂P|T = 0 Again from previous… dh = ∂h/∂T|pd. T+ ∂h/∂P|T d. P Thus dh = Cpd. T Over the temperature rate T 1 to T 2 this is integrated to give….

Specific Heats T 2 h 2 – h 1 = CPd. T T 1 It is often convenient to specify specific heats on a per mole basis rather than per-unit-mass basis. __ __ These molar specific heats are Cv and Cp thus… C__v = MCv and Cp __ = MCp Where M is the molar mass.

Specific Heats The equation for enthalpy can be used to relate for an ideal gas, the specific heats and the gas constant i. e. dh = du + d(Pv) Introducing the specific heat relationships and the ideal gas equation gives… CPd. T = Cvd. T + Rd. T Thus Cp = Cv + R or R = C p – Cv

Specific Heat Ratio We can define the specific heat ratio as… γ = Cp/Cv Thus substituting into… R = Cp – Cv for Cv gives… R = C p – Cp/γ = Cp(γ-1)/γ i. e. Cp = Rγ/(γ-1) Similarly Cv = R/(γ-1)

Specific Heats • Note 1: Since R is a constant for an ideal gas, the specific heat ratio will depend only on temperature • Note 2: For gases, the specific heats slowly increase with increasing temperature. Since they ado not vary significantly over fairly large temperature differences, it often acceptable to treat Cp and Cv as constants. For such cases… u 2 – u 1 = Cv(T 2 – T 1) and h 2 – h 1 = Cp(T 2 – T 1)

Example 1 • At entry to a horizontal steady flow system, a gas has a specific enthalpy of 2000 k. J/kg and possesses 250 k. J/kg of kinetic energy. At the outlet of the system, the specific enthalpy is 1200 k. J/kg and there is negligible kinetic energy. If there I no heat energy transfer during the process determine the magnitude and direction of the work done.

Solution • Using the specific enthalpy form of the steady flow energy equation (SFEE)… Q – W = (h 2 – h 1) + (1/2)(V 22 –V 12)+ g(z 2 – z 1) We note that g(z 2 – z 1) = 0 since there is no change in height between the fluid entry and exit (horizontal). Also there is negligible fluid kinetic energy at exit thus (1/2)V 22 = 0 and during the process Q = 0. Thus SFEE gives… 0 – W = (1200 – 2000) + 0 + (0 – 250) = 1050 k. J/kg As work is positive, work is done by the system.

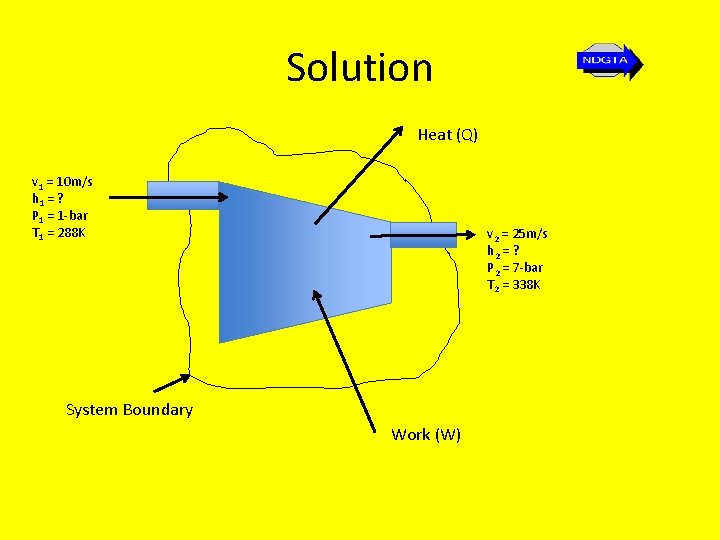
Example 2 • Steady flow air enters the inlet of a horizontal compressor at a velocity of 10 m/s, a pressure of 1 bar and a temperature of 15 o. C. It exits the compressor flowing at 0. 6 kg/s with a velocity of 25 m/s, a pressure of 7 -bar and a temperature of 65 o. C. If the input power to the compressor is 42 k. W and for the air cp = 1. 005 k. J/kg. K and R = 0. 287 k. J/kg. K determine… a. The specific heat energy lost to the surroundings b. The cross sectional area of the compressor exit duct.

Solution Heat (Q) v 1 = 10 m/s h 1 = ? P 1 = 1 -bar T 1 = 288 K v 2 = 25 m/s h 2 = ? P 2 = 7 -bar T 2 = 338 K System Boundary Work (W)

Solution • Using… Q – W = (h 2 – h 1) + (1/2)(V 22 –V 12)+ g(z 2 – z 1) And h 2 – h 1 = cp(T 2 – T 1) In this case because the potential energy of air = 0 (negligible difference in height between inlet and outlet of the compressor) then the specific energy changes imparted to the air and the heat loss to the surroundings are given by the relationship… Q – W = (h 2 – h 1) + (1/2)(V 22 –V 12) i. e. Q – W = cp(T 2 – T 1) + (1/2)(V 22 –V 12)

Solution • The specific work input done on the air (W) can be found from the input power to the compressor and the mass flow rate of the gas from the compressor. • Thus power in to the air = -42 k. J/s (power or work input per second done on the fluid =. negative) and the mass flow rate of air at the exit m = 0. 6 kg/s; therefore the specific work done on the gas at exit is… W = - 42/0. 6 = - 70 k. J/kg

Solution • Thus… Q – (-70) = 1. 005(338 – 288) + [(252 – 102)/2 x 103] i. e. Q = -70 + 50. 25 + 0. 2625 = -19. 48 k. J/kg Thus the heat loss to the surroundings (heat out) = 19. 48 k. J/kg. b) PV = m. RT Thus p 2 VS 2 = RT 2 So that the specific volume at exit is… VS 2 = (287 x 338)/(7 X 105) = 0. 1386 m 3/kg

Solution But ρ = 1/Vs = 1/0. 1386 = 7. 215 kg/m 3 Thus, Area A = m /ρV = 0. 6/(7. 215 x 25) = 3. 326 x 10 -3 m 2