Unit 6 RATIONAL EXPONENTS AND RADICAL FUNCTIONS Unit

Unit 6 RATIONAL EXPONENTS AND RADICAL FUNCTIONS

Unit Essential Question: What are the different properties of exponents and radicals that allow us to solve equations?

Lesson 6. 1 RATIONAL EXPONENTS AND NTH ROOTS

Lesson Essential Question: How are nth roots and rational exponents related and how can they be used to simplify expressions?

Nth Roots

Nth Roots

Rational Exponents: How can we rewrite nth roots as exponents? How can we rewrite exponents as nth roots?

Homework: Pages 417 -418 #’s 3 – 49 odds

Bell Work:

Examples:

Examples:

Lesson 6. 2 APPLY PROPERTIES OF RATIONAL EXPONENTS

Lesson Essential Question: What are the different properties of rational exponents and how are they used to simplify expressions?

Properties of Rational Exponents: Blue Tables on Pages 420 – 421

Examples:

Bell Work:

Homework: Pages 424 – 425 #’s 3 – 65 odds

Bell Work:

Class Work: Pages 424 – 425 #’s 4 – 54 evens This assignment will be collected!!! Small Quiz tomorrow at the beginning of class on Properties of Exponents and Radicals. (NO CALCULATORS!!!)

Bell Work:

Quiz:

Lesson 6. 3 OPERATIONS AND COMPOSITIONS OF FUNCTIONS

Lesson Essential Question: How do we perform operations on functions, and how do we take a composition of two or more functions?

Operations on Functions:

Domain: Remember that domain is the set of all x-values that will work for a given function. When we perform operations, this can sometimes alter the domain of the original functions. Lets look back at the four operations we did, and find the domain for each:

Compositions of Functions:

Notation:

Homework: Page 432 #’s 3 – 37 odds

Bell Work:

Classwork/Homework: This assignment will be collected tomorrow!!! Pages 432 – 433 #’s 4 – 38 evens

Bell Work:

Lesson 6. 4 INVERSE FUNCTIONS

Lesson Essential Question: How do we find an inverse function and how does it relate to its original function? ? ?

Inverse Functions: To prove that two functions are inverses, then the composition of the two functions must come out to be x. If f(x) and g(x) are inverses, then f(g(x)) = x and g(f(x)) = x.

Graphs of Inverse Functions:

If two functions are inverses, then… 1) The composition of the functions will come out to be x. 2) They have reversed x and y values. (This means the domain and range are switched!) 3) The graphs of the functions are reflected about the line y = x.

Notation:

Bell Work:

Steps for finding an inverse function…

Homework: Pages 442 – 443 #’s 3 – 27 odds

Bell Work:

Lesson 6. 6 SOLVING RADICAL EQUATIONS

Lesson Essential Question: How do we solve radical equations and why is it important to check our solutions?

Steps for solving a radical equation: 1) Isolate one of the radicals 2) Raise both sides to a power to cancel out the isolated radical. 3) Repeat steps 1 and 2 if necessary. 4) Solve. 5) Check for extraneous solutions!

Examples:

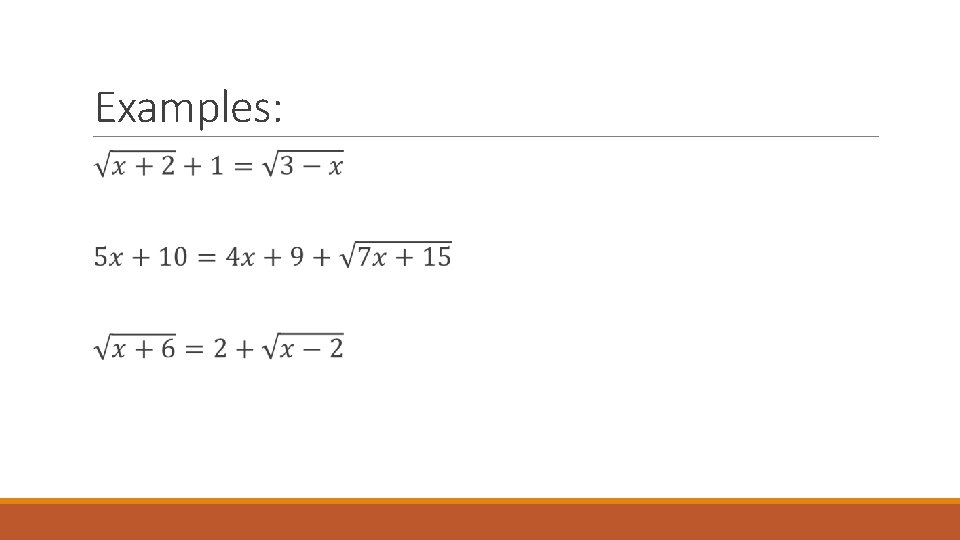
Examples:

Homework: Pages 456 – 457 #’s 3 – 21 odds and 35 – 51 odds

Bell Work:

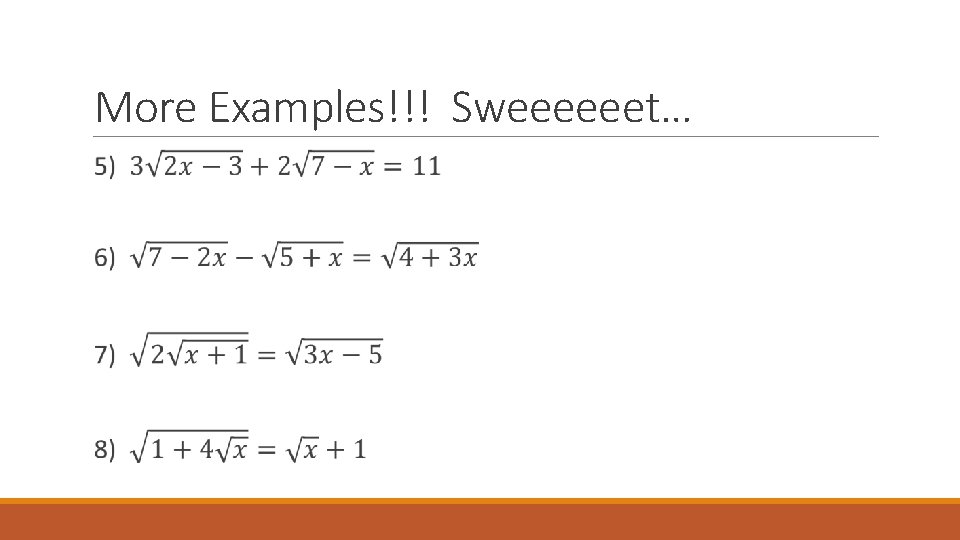
More Examples!!! Sweeeeeet…

Homework: This assignment will be collected!!! Pages 456 – 457 #’s 4, 10, 16, 20, 24, 28, 38, 50, 52

Bell Work:

Unit 6 Test Upcoming!!!!!!!!!!!! Properties of Radicals Properties of Exponents Operations and Compositions of Functions Inverse Functions Solving Radical Equations