Unit 6 Matrices 6 1 Matrix Operations Terminology

Unit 6 - Matrices 6. 1 – Matrix Operations & Terminology

Matrix Operations and Terminology • use matrices to organize data • use matrix operations to discover trends in the data What is a matrix?

Terminology A rectangular arrangement of numbers is called matrix. The plural of matrix is matrices† (not matrixes). The numbers which appear in the matrix are called its entries and are arranged in horizontal rows and vertical columns. How many rows? Columns? What is the entry in row 2 column 4? 12 -9 3 -11 0 7 -14 21 -6 5 20 17

An entry of a matrix is identified by stating its row and column. ex an entry is in the third row and second column, we call it the 32 -entry (read “the three-two entry”) of the matrix. Note: Use double subscripts to specify entries. ex In a matrix A, we could refer to the 32 -entry as a 32. Note: A matrix is enclosed in square brackets and label it with a capital letter. i. e. A = [2 13 6] has three entries. How would you label the entry 13?

Let’s look at some examples Example 1 -The data in matrix V represents TV viewing hours of both men and women. V= 4. 2 2. 7 2. 6 2. 5 2. 9 2. 0 2. 3 5. 8 8. 3 5. 2 7. 9 What are the entries in the first row of V? Circle the second column of V? What is the 13 -entry of V? Identify the entry 2. 6. What is the value of v 2, 3?

Your Turn Example 2 Using V = 4. 2 2. 7 2. 6 2. 5 2. 9 2. 0 2. 3 5. 8 8. 3 5. 2 7. 9 a) Which is the 32 -entry of V? b) The value 2. 3 is which entry of V?

More Terms A matrix with m rows and n columns has size or dimension “m by n. ” Written as m× n. A square matrix has the same number of rows and columns. Note: If A is an n × n matrix, the entries a 11, a 22, a 33, . . . , ann are called main diagonal entries

Here’s another example Example 3 Matrix A = Matrix B = 12 8 15 17 52 3 21 72 43 23 67 11 3 4 22 45 16 6 4 86 26 State the dimensions of Matrix A. Matrix B. Is either A or B a square matrix? Explain What are the main diagonal entries of each matrix?

Your Try this one!! Example 4 Matrix A = 2 54 72 3 7 5 4 68 3 16 9 0 What are the dimensions of A? What are the entries on A’s main diagonal? 7 11 13

A few more definitions Two matrices are equal if they have the same dimension and if corresponding entries in the two matrices are equal. Example 5 - Are these two matrices equal? Justify your response. 5 3 6 0 8 0 5 3 12/2 0 5 23 4 -22

Using Matrices to Organize Data Example 6 – Ninety-two percent of the areas zoned for commercial use last year are still commercial. The remaining 8 percent changed to residential. Eighty-seven percent of the residential areas remained residential, 12 percent were converted to commercial, and 1 percent changed to open land. Eighty-nine percent of the open land remained open, 4 percent became commercial, and 7 percent became residential. Organize this information in a matrix. L= . 92. 12. 04 . 08. 87. 07 . 00. 01. 89

Basic Operations – Sums – Differences – Scalar Multiplication

Operations with Matrices If A and B are two matrices with the same dimension, m × n, then: The sum of A and B, written A + B, is an m n matrix such that each entry of A +B is the sum of corresponding entries in A and B. The difference of A and B, written A - B, is an m n matrix such that each entry of A -B is the difference of corresponding entries in A and B. The scalar multiple of a matrix C, written as, C, where s is a real Number, is matrix whose entries are s times corresponding entries of C.

Properties of Matrices Property Closure A B is a matrix. Associativity (A + B) + C = A + (B + C) Commutativity A+B=B+A Additive inverses There exists a matrix –A such that A + (-A) =0 Identity element A + exist for addition 0 0 = 0 0 +A = A

Associative Property Example 7 Use matrices A, B, and C to illustrate the associative property for matrix addition. A= 3 0 7 13 B= -5 12 4 20 C= 28 10 -5 3

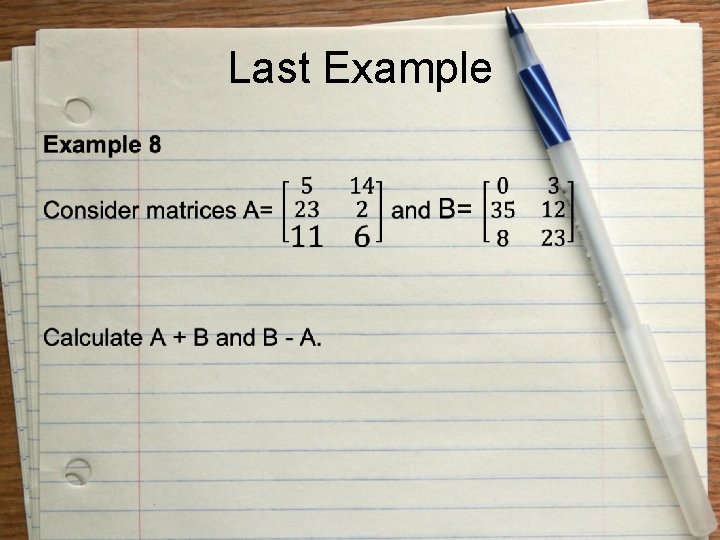
Last Example

What’s Next… Classwork / Homework for today: • Practice 4 -1 AND 4 -2 WS • Both Sheets • Posted on GC • Due Tuesday, 11/10 at midnight