UNIT 6 EXPONENTIAL AND LOGARITHMIC FUNCTIONS Section 2

UNIT 6 EXPONENTIAL AND LOGARITHMIC FUNCTIONS Section 2 – Graphing Exponential and Logarithm Functions

Graphing Exponentials Supplemental Packet pg. 73 Parent Function is y = bx and it’s chart values will change depending on what b is. We will use -2, -1, 0, 1, 2 for the x values. Example 1: y = (3)x x | -2 | -1 | 0 | 1 | 2 | y | 1/9 | 1/3 | 1 | 3 | 9 | Notice -2 and -1 produce fractions, 3 -2 is 1/9 because negative exponents means reciprocal.

Graphing Exponentials Supplemental Packet pg. 73 B) y = ( ½ )x x | -2 | -1 | 0 | 1 | 2 | y | 4 | 2 | 1 | ½ | ¼ | Notice the fractions are now with 1 and 2, since b is a fraction. Asymptote – A line that a curve continually approaches but does not meet. For parent functions, y = 0 is the asymptote

Graphing Exponentials TRANSLATIONS a, k and h translate the function just as they have for all other functions. The Asymptote is horizontal. What will make the asymptote move? It will only move up or down, so k will move it. For translated functions, asymptote is y = k .

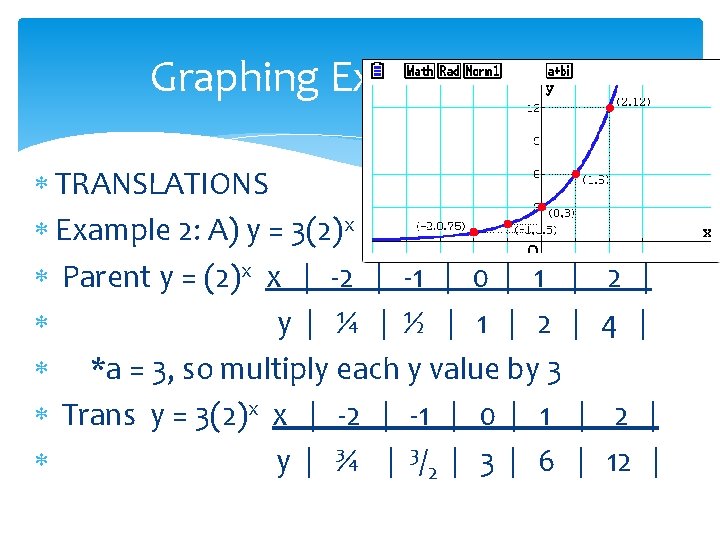
Graphing Exponentials TRANSLATIONS Example 2: A) y = 3(2)x Parent y = (2)x x | -2 | -1 | 0 | 1 | y | ¼ | ½ | 1 | 2 | *a = 3, so multiply each y value by 3 Trans y = 3(2)x x | -2 | -1 | 0 | 1 | y | ¾ | 3 /2 | 3 | 6 | 2 | 4 | 2 | 12 |

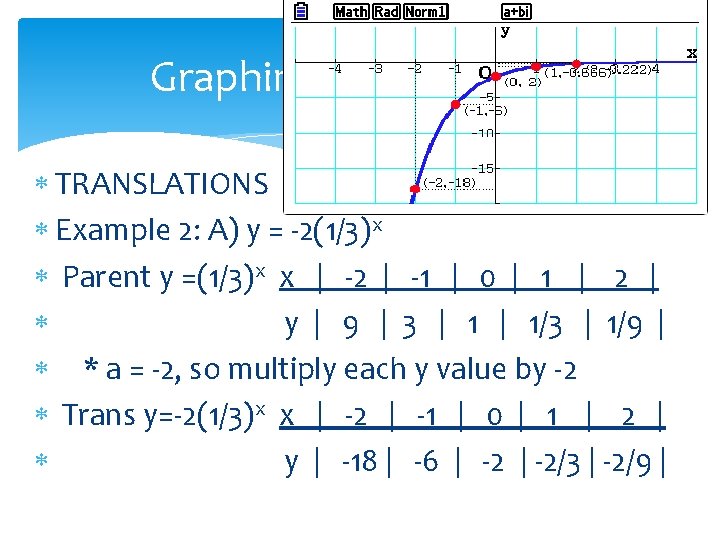
Graphing Exponentials TRANSLATIONS Example 2: A) y = -2(1/3)x Parent y =(1/3)x x | -2 | -1 | 0 | 1 | 2 | y | 9 | 3 | 1/3 | 1/9 | * a = -2, so multiply each y value by -2 Trans y=-2(1/3)x x | -2 | -1 | 0 | 1 | 2 | y | -18 | -6 | -2/3 | -2/9 |

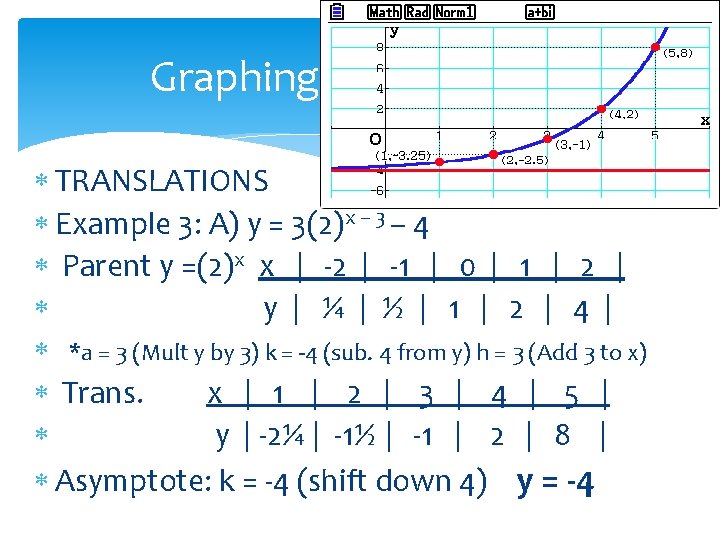
Graphing Exponentials TRANSLATIONS Example 3: A) y = 3(2)x – 3 – 4 Parent y =(2)x x | -2 | -1 | 0 | 1 | 2 | y | ¼ | ½ | 1 | 2 | 4 | *a = 3 (Mult y by 3) k = -4 (sub. 4 from y) h = 3 (Add 3 to x) Trans. x | 1 | 2 | 3 | 4 | 5 | y | -2¼ | -1½ | -1 | 2 | 8 | Asymptote: k = -4 (shift down 4) y = -4

Graphing Exponentials TRANSLATIONS Example 3: B) y = ( ½ )x + 5 + 2 Parent y =( ½ )x x | -2 | -1 | 0 | 1 | 2 | y | 4 | 2 | 1 | ½ | ¼ | *k = 2 (add 2 to y) h = -5 (Sub. 5 from x) Trans. x | -7 | -6 | -5 | -4 | -3 | y | -2¼ | -1½ | -1 | 2 | 8 | Asymptote: k = 2 (shift up 2) y = 2

Graphing Exponentials PRACTICE: supplemental packet pg. 74: 1 - 9

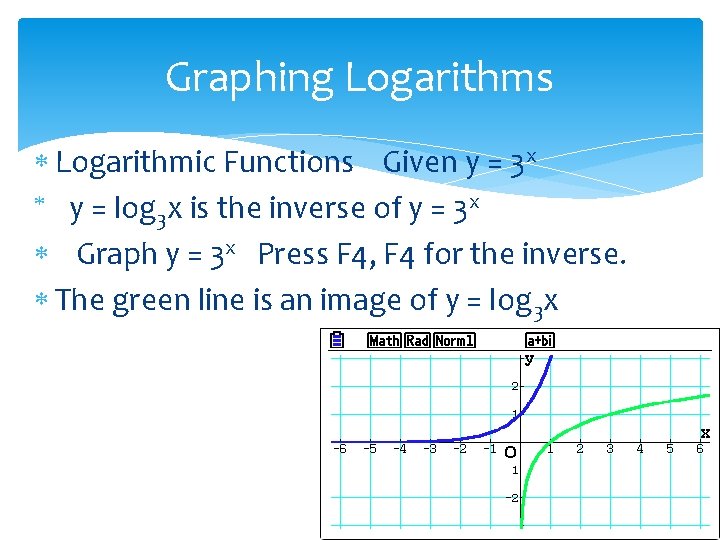
Graphing Logarithms Logarithmic Functions Given y = 3 x y = log x is the inverse of y = 3 x 3 Graph y = 3 x Press F 4, F 4 for the inverse. The green line is an image of y = log 3 x

Graphing Logarithms Evaluating Logarithms (Packet p. 75) y = bx Inverse is x = by is equivalent to y = logbx Therefore, y = bx y = logbx Example 1: log 525 = x Exponential form: 5 x = 25 PRACTICE: 10 - 14

Graphing Logarithms Evaluating Logarithms (Packet p. 75) Therefore, y = bx y = logbx Example 2: Evaluate log 464 = x 4 x = 64 x=3 In other words, log 464 is asking 4 to what exponent would equal 64. 43 = 64 so x = 3 Practice p. 73: 1 – 53

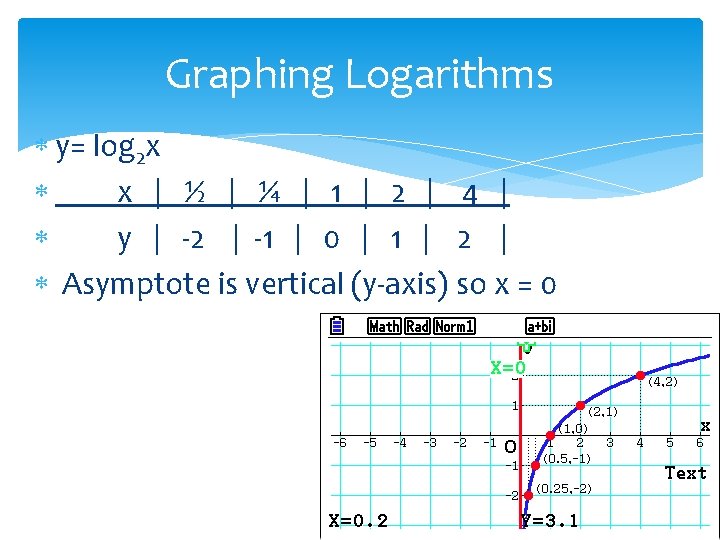
Graphing Logarithms Translating Logarithmic Functions (Packet p. 76) y= log 2 x means if x = 8, then log 28 = 3 since 23 = 8 We will use x values that work for base 2 x | ½ | ¼ | 1 | 2 | 4 | y | -2 | -1 | 0 | 1 | 2 | *Notice that this is the inverse of y = 2 x, the x and y values are switched.

Graphing Logarithms y= log 2 x x | ½ | ¼ | 1 | 2 | 4 | y | -2 | -1 | 0 | 1 | 2 | Asymptote is vertical (y-axis) so x = 0

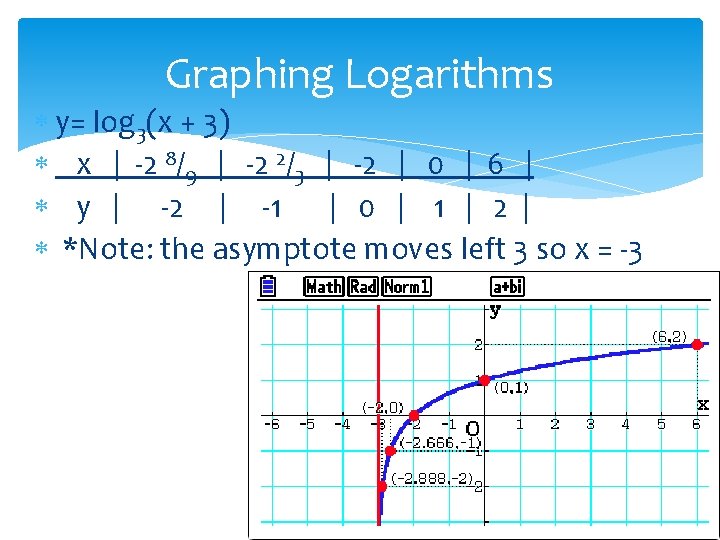
Graphing Logarithms y = logb(x - h) + k OR y =k + log 3(x – h) y= log 3(x + 3) h = -3 (shift left 3) y = log 3 x x | 1/9 | 1/3 | 1 | 3 | 9 | y | -2 | -1 | 0 | 1 | 2 | h = -3 , Subtract 3 from x. x | -2 8/9 | -2 2/3 | -2 | 0 | 6 | y | -2 | -1 | 0 | 1 | 2 | *Note: the asymptote also moves left 3 so x = -3 Asymptote will always be x = h

Graphing Logarithms y= log 3(x + 3) x | -2 8/9 | -2 2/3 | -2 | 0 | 6 | y | -2 | -1 | 0 | 1 | 2 | *Note: the asymptote moves left 3 so x = -3

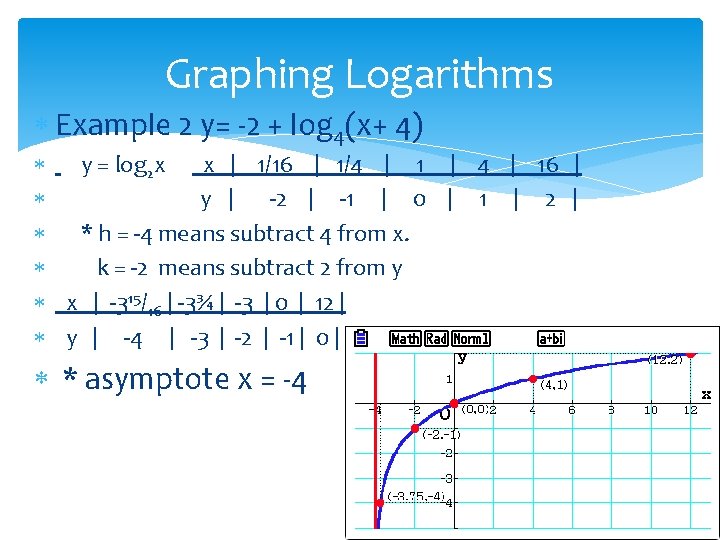
Graphing Logarithms Example 2 y= -2 + log 4(x+ 4) y = log 2 x x | 1/16 | 1/4 | 1 | 4 | 16 | y | -2 | -1 | 0 | 1 | 2 | * h = -4 means subtract 4 from x. k = -2 means subtract 2 from y x | -315/16 | -3¾ | -3 | 0 | 12 | y | -4 | -3 | -2 | -1 | 0 | * asymptote x = -4

Graphing Logarithms PRACTICE: packet p. 76: 62 - 74