Unit 6 Circular Motion Gravitation Part 1 Circular

Unit 6: Circular Motion & Gravitation Part 1 – Circular Motion

Table of Contents Uniform Circular Motion Defined Examples of Circular Motion and Centripetal Force Circular Motion & Angular Velocity Direction of Centripetal Force & Centrifugal “Force” Calculating Centripetal Acceleration and Force Using Rotational Motion to Simulate Gravity in Space

Uniform Circular Motion – Motion along a circular path at a constant speed. Could we say “at a constant velocity”? No! Velocity is a vector! If direction is changing, that means velocity is changing. If velocity is changing, that means we have acceleration. If we have acceleration, that means we have a net force. Any force that causes an object to move in a circular path is called a centripetal force.

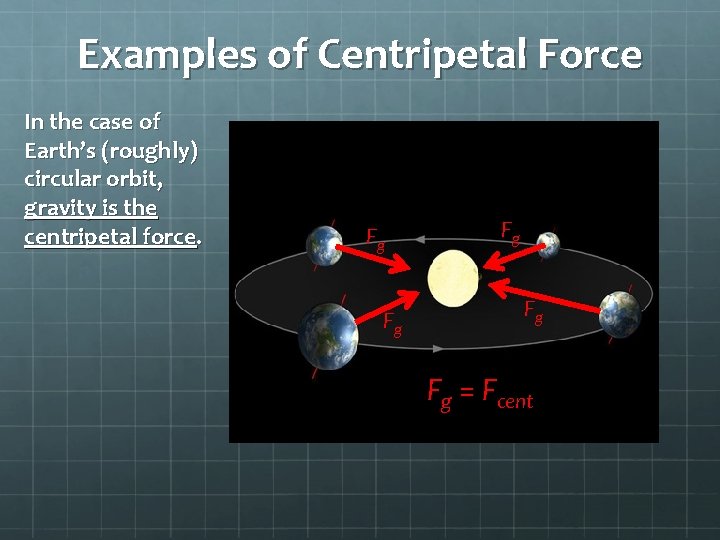
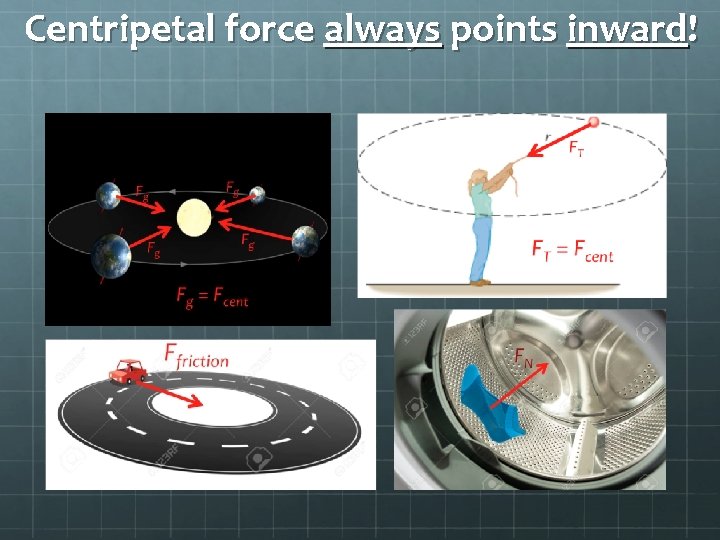
Examples of Centripetal Force In the case of Earth’s (roughly) circular orbit, gravity is the centripetal force. Fg Fg Fg = Fcent

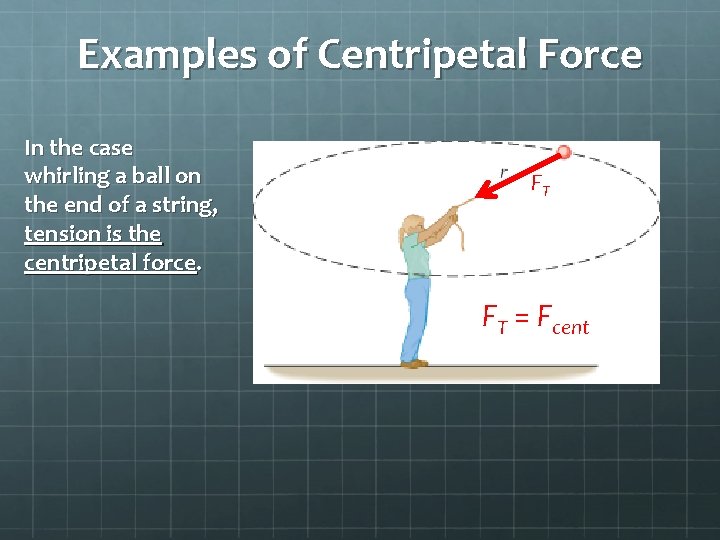
Examples of Centripetal Force In the case whirling a ball on the end of a string, tension is the centripetal force. FT FT = Fcent

Examples of Centripetal Force In the case of a sock going in circles during a washing machine’s spin cycle, the normal force of the wall of the washing machine is the centripetal force. FN FN = Fcent

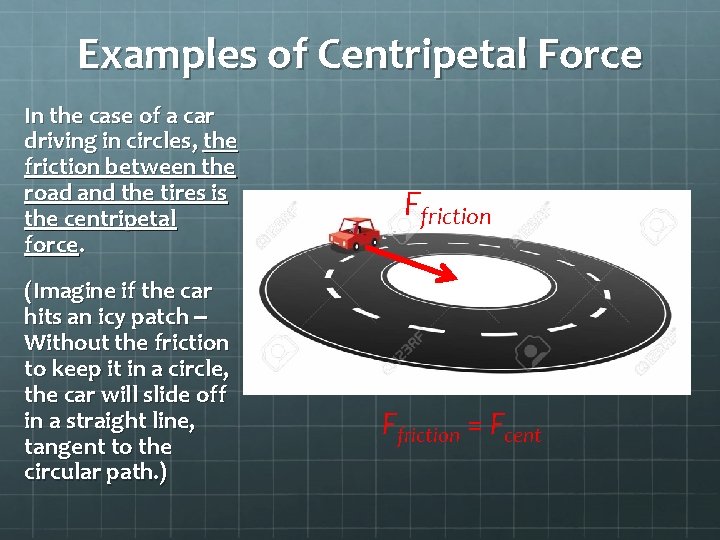
Examples of Centripetal Force In the case of a car driving in circles, the friction between the road and the tires is the centripetal force. (Imagine if the car hits an icy patch – Without the friction to keep it in a circle, the car will slide off in a straight line, tangent to the circular path. ) Ffriction = Fcent

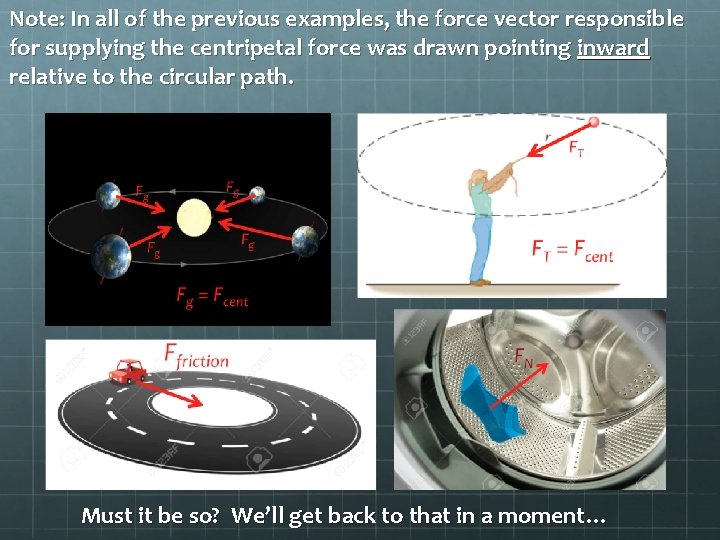
Note: In all of the previous examples, the force vector responsible for supplying the centripetal force was drawn pointing inward relative to the circular path. Must it be so? We’ll get back to that in a moment…

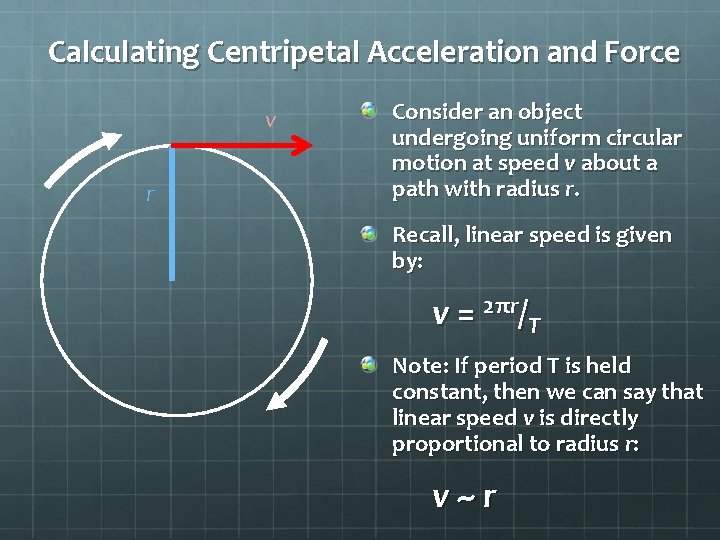
Linear Speed v. Angular Speed When describing the motion of an object traveling in circles, you can describe how fast it’s going either in terms of how quickly it’s covering distance (linear speed) or how quickly it’s completing circles (angular speed) Let’s apply the formula for constant speed to circular motion: v = s/t becomes v = 2πr/T Where: 2πr is the circumference of the circular path T is the period of circular motion, i. e. the time it takes to complete exactly one circle If you know the circumference of the path and how long it takes to complete the path, you calculate v, the linear speed of the object.

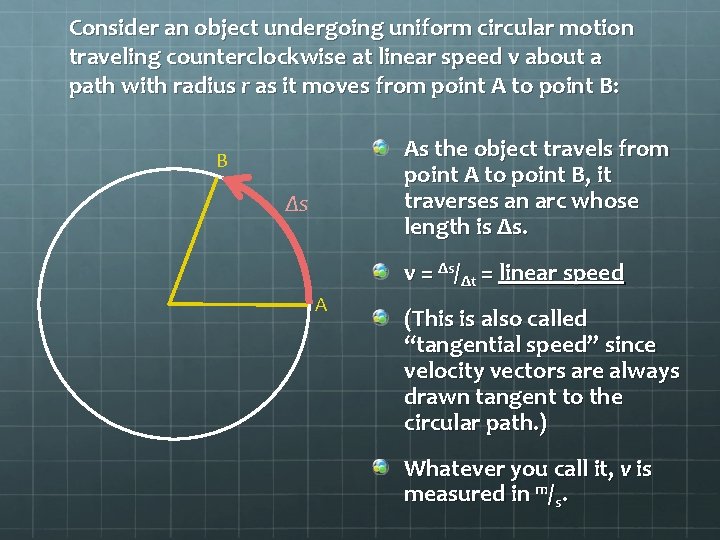
Consider an object undergoing uniform circular motion traveling counterclockwise at linear speed v about a path with radius r as it moves from point A to point B: As the object travels from point A to point B, it traverses an arc whose length is Δs. B Δs v = Δs/Δt = linear speed A (This is also called “tangential speed” since velocity vectors are always drawn tangent to the circular path. ) Whatever you call it, v is measured in m/s.

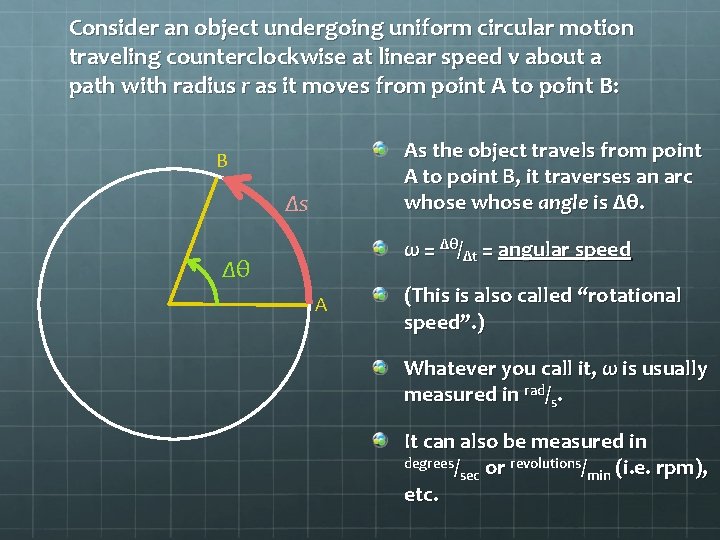
Consider an object undergoing uniform circular motion traveling counterclockwise at linear speed v about a path with radius r as it moves from point A to point B: As the object travels from point A to point B, it traverses an arc whose angle is Δθ. B Δs ω = Δθ/Δt = angular speed Δθ A (This is also called “rotational speed”. ) Whatever you call it, ω is usually measured in rad/s. It can also be measured in degrees/ revolutions/ sec or min (i. e. rpm), etc.

Imagine you have a vinyl record*. Linear Speed v. Angular Speed *If you don’t know, ask your parents or a hipster friend. Suppose two bugs land on the record while it’s set to 33 rpm. Which bug has the greatest angular speed? “Weird Al” Yankovic Neither! They’re both traveling at 33 rpm. They complete circles at the same rate! Which bug has the greater linear speed? The outer bug! It travels a larger circumference in the same amount of time the inner bug travels a smaller circle.

Period, Frequency, and “Rotational Frequency” Let T = the period of circular motion, i. e. the time it takes for one full circle. “Frequency” is the inverse of period; it is a measure of how often cycles occur. (We’ll study this phenomenon in much greater detail in Unit 4). Frequency is given by: f = 1/T If T is measured in sec, then frequency is in s-1 (which is the same thing as Hz) Note: angular speed ω is sometimes called “angular frequency” If ω is measured in radians/sec, then it is given by ω = 2π/T Note: You can also write ω = 2πf ω is a measure of how often radians are traveled; f is a measure of how often full circles are traveled. So “frequency” f and “rotational frequency” ω differ by a factor of 2π.

Connecting Linear & Angular Speeds Recall that linear speed may be expressed v = 2πr/T Divide both sides by radius: v/r = 2π/T But ω = 2π/T So, v/r = ω Thus, v = ωr

How does this work with units? v = ωr Rad/ meters/ sec meters sec Where did the radians go? ? ?

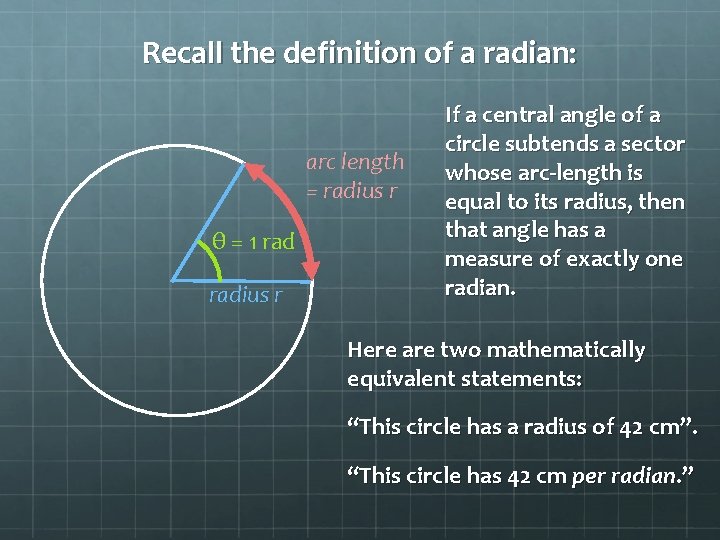
Recall the definition of a radian: arc length = radius r θ = 1 radius r If a central angle of a circle subtends a sector whose arc-length is equal to its radius, then that angle has a measure of exactly one radian. Here are two mathematically equivalent statements: “This circle has a radius of 42 cm”. “This circle has 42 cm per radian. ”

So the units of radius can be thought as being meters per radian v = ωr rad/ sec meters/ radian

So the units of radius can be thought as being meters per radian v = ωr rad/ meters/ sec meters/ radian

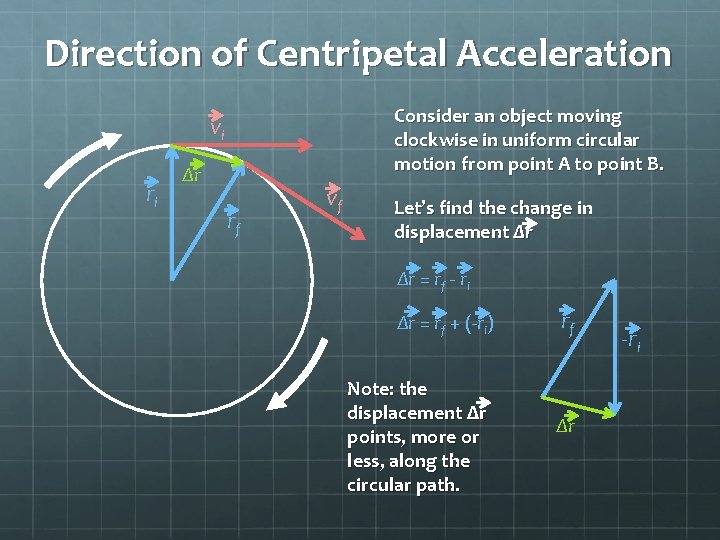
Direction of Centripetal Acceleration Consider an object moving clockwise in uniform circular motion from point A to point B. vi ri Δr rf vf Let’s find the change in displacement Δr Δr = rf - ri Δr = rf + (-ri) Note: the displacement Δr points, more or less, along the circular path. rf Δr -ri

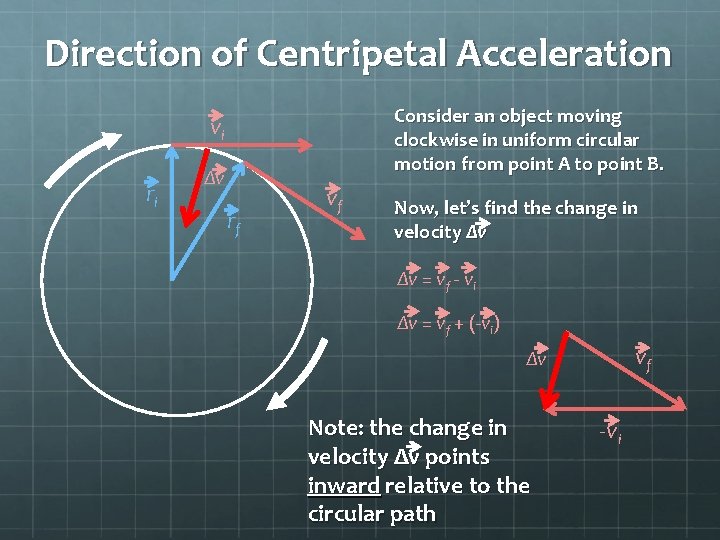
Direction of Centripetal Acceleration Consider an object moving clockwise in uniform circular motion from point A to point B. vi ri Δv rf vf Now, let’s find the change in velocity Δv Δv = vf - vi Δv = vf + (-vi) vf Δv Note: the change in velocity Δv points inward relative to the circular path -vi

Direction of Centripetal Acceleration If an object is experiencing uniform circular motion, its velocity is constantly changing. The direction of the change-in-velocity vector Δv always points inward relative to the circular path. Since velocity is changing, there must be acceleration. The acceleration an object in uniform motion experiences is called “centripetal acceleration”. Since a = Δv/Δt, the centripetal acceleration vector must point in the same direction as the change-in-velocity vector. Thus centripetal acceleration always points inward.

Direction of Centripetal Force Any object undergoing uniform circular motion is experiencing centripetal acceleration. Since the object undergoing uniform circular motion is accelerating, Newton’s laws demand there must be a nonzero net force present causing this acceleration. This force, whatever the nature of it is, is called the “centripetal force” Furthermore, since F = ma, this force must point in the same direction as acceleration. Thus centripetal forces always point inward, relative to the circular path.

Centripetal force always points inward!

That all centripetal forces are inward can seem counterintuitive. For example: When you open a washing machine after the spin cycle, are the clothes evenly spread throughout the washer, gathered near the center, or spread around at the edges? They’ll be spread around at the edges! (And if you didn’t know this – Shame on you! You’re old enough to help around the house by now!) Anyway, given that the laundry gathers at the outer part of the washer during the spin cycle, it would seem intuitively obvious, even to the most casual observer, that there must have been an outward force acting on the clothes. But let’s consider this more carefully…

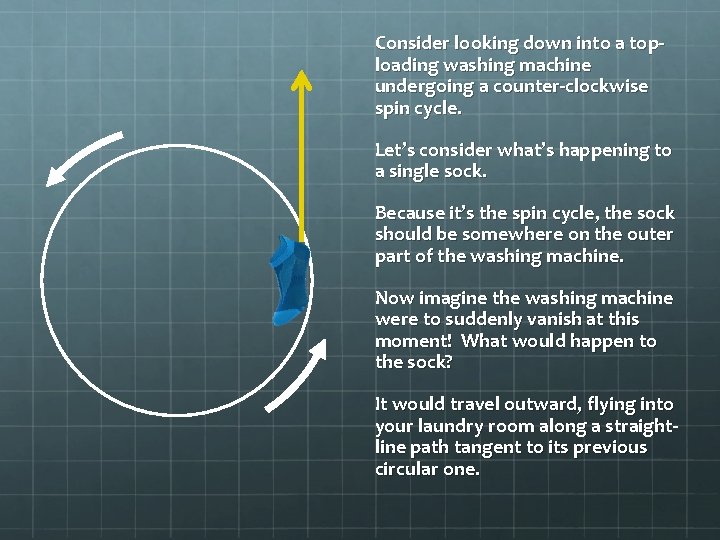
Consider looking down into a toploading washing machine undergoing a counter-clockwise spin cycle. Let’s consider what’s happening to a single sock. Because it’s the spin cycle, the sock should be somewhere on the outer part of the washing machine. Now imagine the washing machine were to suddenly vanish at this moment! What would happen to the sock? It would travel outward, flying into your laundry room along a straightline path tangent to its previous circular one.

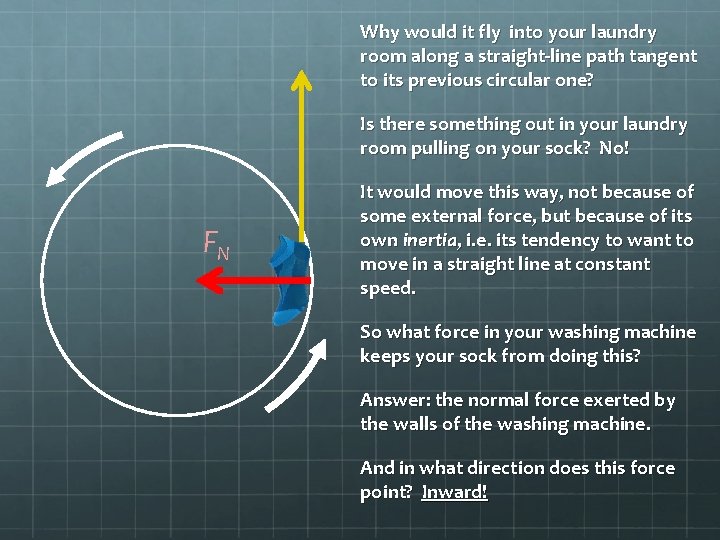
Why would it fly into your laundry room along a straight-line path tangent to its previous circular one? Is there something out in your laundry room pulling on your sock? No! FN It would move this way, not because of some external force, but because of its own inertia, i. e. its tendency to want to move in a straight line at constant speed. So what force in your washing machine keeps your sock from doing this? Answer: the normal force exerted by the walls of the washing machine. And in what direction does this force point? Inward!

Here’s another example: Let’s say you’re a passenger in a car driving quickly in a counterclockwise circle. As you imagine the car rounding this curve, you probably envision yourself feeling compelled to lean toward your right – it feels like there’s an outward force. Is there anything outside of the circular path pulling you toward the right? No! There is nothing pulling or pushing you to the right! So why does it feel like there is? ? ?

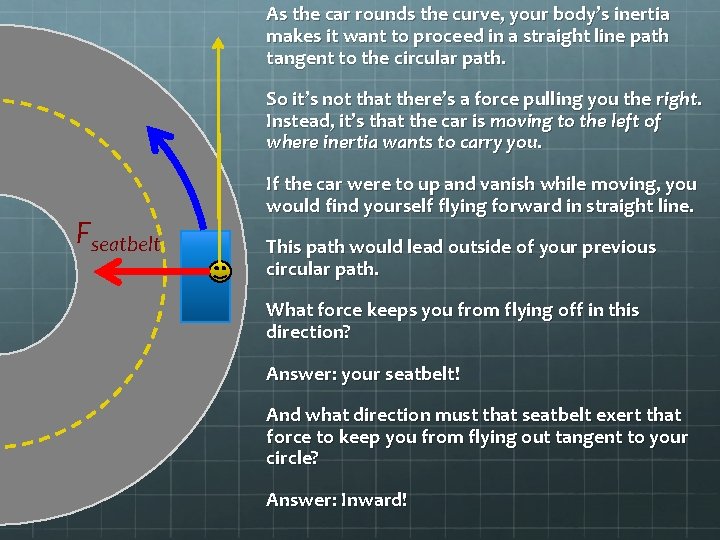
As the car rounds the curve, your body’s inertia makes it want to proceed in a straight line path tangent to the circular path. So it’s not that there’s a force pulling you the right. Instead, it’s that the car is moving to the left of where inertia wants to carry you. Fseatbelt If the car were to up and vanish while moving, you would find yourself flying forward in straight line. This path would lead outside of your previous circular path. What force keeps you from flying off in this direction? Answer: your seatbelt! And what direction must that seatbelt exert that force to keep you from flying out tangent to your circle? Answer: Inward!

Centrifugal “Force” This illusion of an outward force during uniform circular motion is called centrifugal “force”. Centrifugal “force” is NOT an actual force. It is not due to something actually pulling or pushing another object. It is due to inertia. The fact that an object’s inertia makes it want to travel in a straight line makes it seem like there’s an outward force when it’s forced to move in a circle instead. Since it’s not a real force, centrifugal “force” is sometimes called a “fictitious force”.

Calculating Centripetal Acceleration and Force v r Consider an object undergoing uniform circular motion at speed v about a path with radius r. Recall, linear speed is given by: v = 2πr/T Note: If period T is held constant, then we can say that linear speed v is directly proportional to radius r: v~r

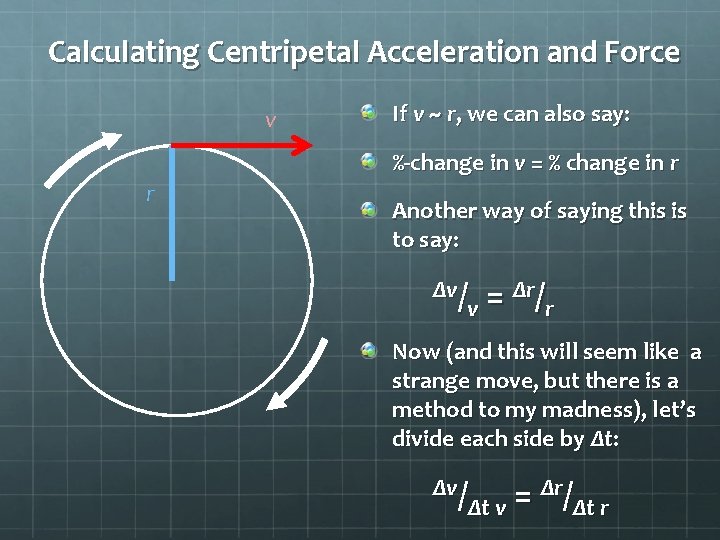
Calculating Centripetal Acceleration and Force v If v ~ r, we can also say: %-change in v = % change in r r Another way of saying this is to say: Δv/ = Δr/ v r Now (and this will seem like a strange move, but there is a method to my madness), let’s divide each side by Δt: Δv/ Δr/ = Δt v Δt r

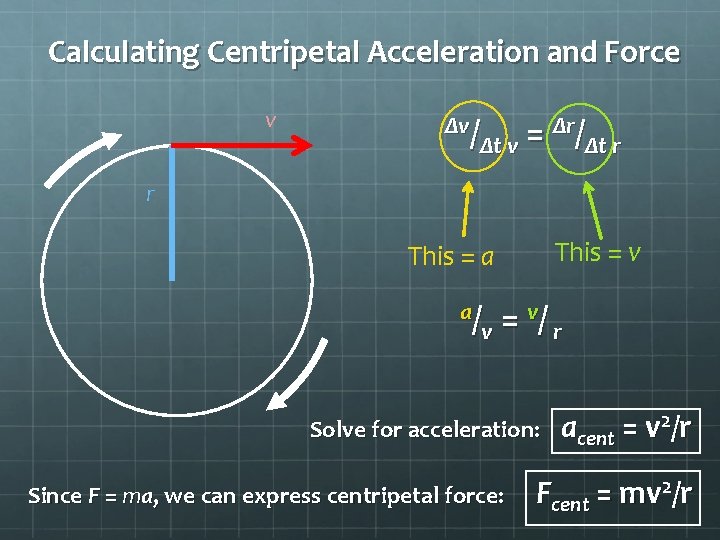
Calculating Centripetal Acceleration and Force v Δv/ Δr/ = Δt v Δt r r This = v This = a a / = v/ v r Solve for acceleration: Since F = ma, we can express centripetal force: acent = v 2/r Fcent = mv 2/r

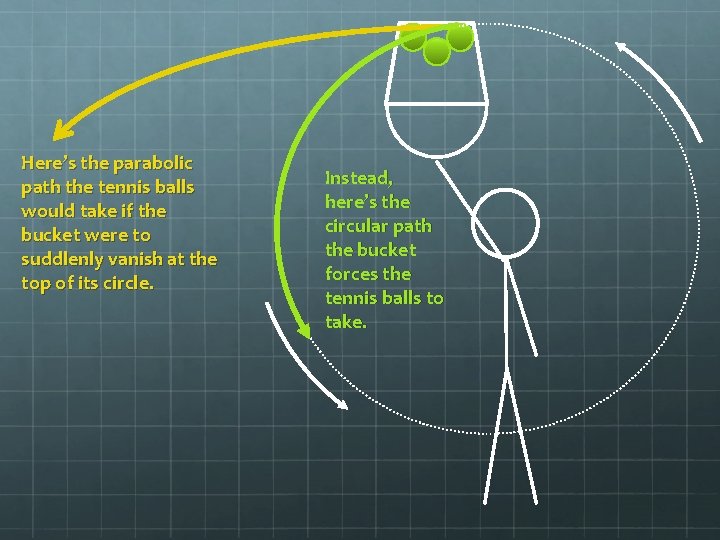
Example problem: A) If the distance from your shoulder to the bottom of a bucket is 1. 12 m, how fast would you have to whirl a bucket full of tennis balls in order to keep them in the bucket? First of all, you might be tempted to ask, “Why don’t the tennis balls fall if you whirl the bucket fast enough? ” But this question is actually based on a false premise. The circular motion actually forces the tennis balls to move downward faster than if gravity were the only force!

Here’s the parabolic path the tennis balls would take if the bucket were to suddlenly vanish at the top of its circle. Instead, here’s the circular path the bucket forces the tennis balls to take.

Getting back to the problem: In order for the tennis balls to stay in the bucket, the centripetal force of the bucket acting on them must dominate over gravity: Fcent ≥ Fg mv 2/r ≥ mg v 2/r ≥ g v 2 ≥ rg v ≥ √(rg) v ≥ √(1. 12 m × 9. 8 m/s 2) v ≥ 3. 3 m/s

Another example problem: B) An amusement park ride at the county fair takes passengers in a vertical circle, 42 -m in diameter, at a constant speed of 18 m/s. With how much force would a 72 -kg person feel pressed into their seat when they are at the bottom of the circular path? Since motion is uniform and circular, we know that the net force must be a centripetal force, and thus point inward, relative to the circular path. Thus, when we draw the free body diagram, we know to draw the normal force vector longer than force due to gravity. FN Fg

Another example problem: B) An amusement park ride at the county fair takes passengers in a vertical circle, 42 -m in diameter, at a constant speed of 18 m/s. With how much force would a 72 -kg person feel pressed into their seat when they are at the bottom of the circular path? From the free-body diagram we can see that Fnet = FN - Fg And since Fnet = Fcent = FN - Fg FN Fg The force that we’re trying to find is the normal force: FN = Fcent – Fg FN = mv 2/r – mg FN = (72 kg)(18 m/s)2/(21 m) = 1100 N

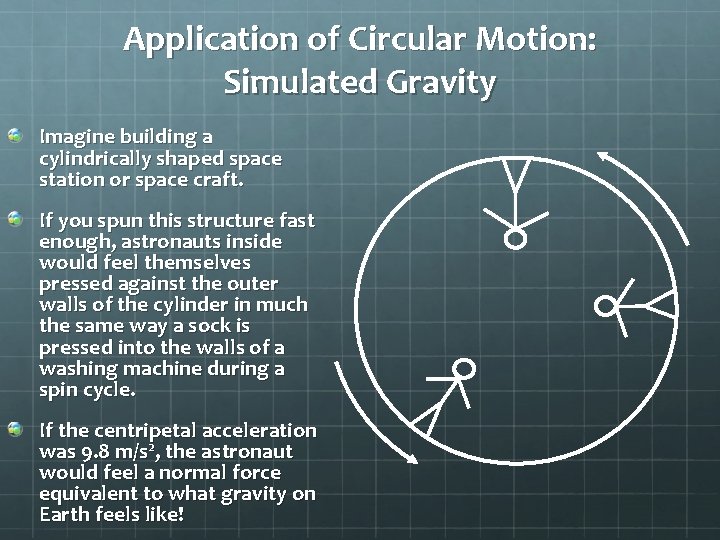
Application of Circular Motion: Simulated Gravity Imagine building a cylindrically shaped space station or space craft. If you spun this structure fast enough, astronauts inside would feel themselves pressed against the outer walls of the cylinder in much the same way a sock is pressed into the walls of a washing machine during a spin cycle. If the centripetal acceleration was 9. 8 m/s 2, the astronaut would feel a normal force equivalent to what gravity on Earth feels like!

Application of Circular Motion: Simulated Gravity This method of simulated gravity has been depicted in many science fiction movies, including recent films like Interstellar and The Martian. Let’s take a look at such a movie: Mission to Mars. Let’s analyze the clip below to see if this scene accurately portrays simulated gravity through rotational motion. When you watch the clip, make a note of timing in order to get an estimate for the rotational period of the spaceship, and make a note of how wide the craft seems to be relative to the actors in order to estimate radius. https: //www. youtube. com/watch? v=QMZCmg. YITg. Q

Mission to Mars Analysis Have you watched the clip yet? Now’s your last chance before spoilers!!! Note: The actress featured during the clip appeared to be totally horizontal at the 0: 12 mark, and then totally vertical at the 0: 24 mark. If it takes 12 seconds to go ¼ of the way around, we can deduce that the rotational period T of the spaceship is approximately 48 seconds. Also note: At the 1: 07 mark you can compare the height of the actor on screen with the radius of the space craft. His height appears to be around 2/5, or 40%, of the radius. If he’s around 2 -m tall, we can guesstimate the radius r of the craft to be around 5 meters

Mission to Mars Analysis Given T = 48 s and r = 5 m, what is the centripetal acceleration the astronauts should be feeling inside this ship, and how does this compare to gravity? First, let’s find linear speed v: v = 2πr/T = 2π× 5 m/48 s = 0. 654 m/s Now let’s find centripetal acceleration: acent = v 2/r = (0. 654 m/s)2/(5 m) = 0. 0855 m/s 2, or about 0. 09 m/s 2 This is less than one percent of gravitational acceleration 9. 8 m/s 2! That’s not exactly what was depicted in the movie!

Mission to Mars Analysis So how fast would a 5 -m radius spaceship need to rotate in order to simulate Earth gravity? Solve the centripetal acceleration formula for linear speed: acent = v 2/r v = √(ar) If a = 9. 8 m/s 2 and r = 5 m, then v = √(9. 8 m/s 2 × 5 m) = 7 m/s What would the rotational period be? v = 2πr/T T = 2πr/v = 2π× 5 m/7 m/s = 4. 5 s Divide 60 s by this number to get rotational speed: 13 rpm!

Mission to Mars Analysis A spaceship rotating at 13 rpm would be crazy fast! Also, if an astronaut were standing, then 9. 8 m/s 2 would be the magnitude of simulated gravity they felt at their feet. Their head would be significantly closer to the spin axis, and would therefore feel a very different centripetal force. This gradient of different simulated gravity felt across one’s body, especially as it would change as you stood up, sat down, and moved around, would probably result in severe gastrointestinal consequences. For these reasons, an actual space craft employing rotation to simulate gravity would likely be a much larger structure than the small ship shown in the film. Now one thing the movie got right was that if you were in a chamber in the center of the craft, you could float and experience weightlessness while the spaceship simply rotated around you.