UNIT 5 POLYNOMIAL FUNCTION LESSON 5 4 KEY

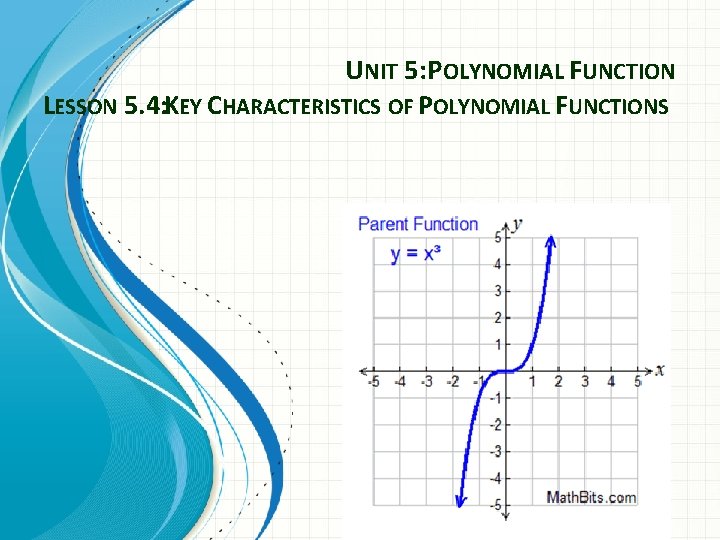
UNIT 5: POLYNOMIAL FUNCTION LESSON 5. 4: KEY CHARACTERISTICS OF POLYNOMIAL FUNCTIONS

Do Now The zeros of a polynomial function are 2, 1, and 3 Write the zeros as factors. Write the equation of the polynomial function by multiplying the factors.

ACT Practice An integer, x, is subtracted from 6. That difference is then multiplied by 3. This product is 15 more than half the original integer. Which of the following Equations represents this relationship?

Objectives Students would be able to: • Interpret polynomial key characteristics in the context of a problem situation. • Generalize the key characteristics of polynomials. Mastery is evidenced by scoring a 3 out of 4 on the Exit Slip

Terms to Know Absolute maximum Absolute minimum Extrema

Common Core Standards A-APR - 3: Understand the relationship between zeros and factors of polynomials. F-BF – 4: Interpret functions that arise in applications in terms of the context.

Problem 1: Math World vs. Real World – Textbook page 370 Work with a partner to answer questions 1 through 5 pages 371 and 372. Set your graphing calculator window to: x-min: -5 x-max: 50 y-min: -5000 y-max: 15000

Guided Questions Is the length of the study the same as the domain of the problem situation? What is the length of the study? Is the average number of frogs the same as the range of the problem situation? What was the lowest average number of frog eggs observed? What was the highest average number of frog eggs observed? Is the domain of the quartic function the same as the domain of the quadratic function? Where is the lowest point on the graph of the quartic function? What are the coordinates of the lowest point on the graph of the quartic function? Is the domain/range of the problem situation the same as the domain of the quartic function? Why and why not? How did you determine the number of frog eggs at 50 months? Why would there be an infinite number of frog eggs if the study lasted forever? Is it possible to have a negative number of frog eggs? At which points on the graph of the quartic function are there 0 frog eggs? What is the significance of the x-intercept / y-intercept with respect to this problem situation? How many intervals are increasing / decreasing? What is the degree of this function?

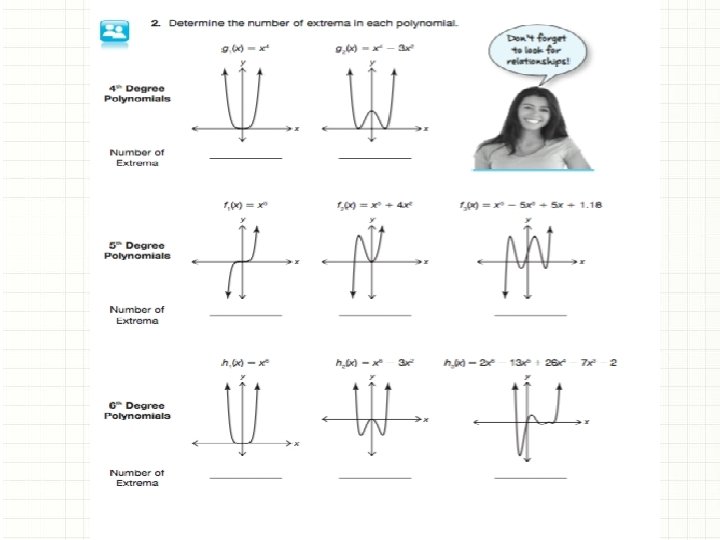
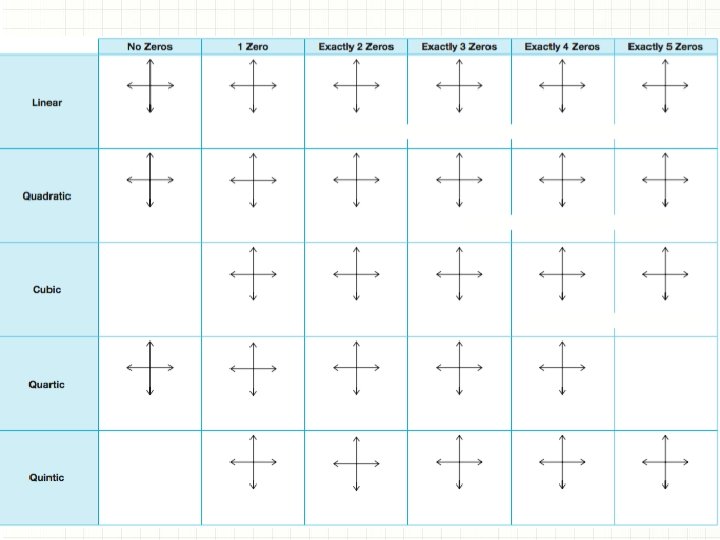
Number of Exterma Maximum number of exterma is one less the function degree. The possible number of exterma is always a difference of 2. Odd degree has a number of exterma that is even, while an even degree has number of exterma that is odd. 9 th degree polynomial : 0, 2, 4, 6, and 8 18 th degree polynomial: 1, 3, 5, 7, 9, 11, 13, 15, and 17