UNIT 5 POLYNOMIAL FUNCTION LESSON 5 2 POWER

UNIT 5: POLYNOMIAL FUNCTION LESSON 5. 2: POWER FUNCTIONS

Do Now Complete the 5. 1 Exit Slip

ACT Practice Questions a. 10 b. 16 c. 58 d. 79 e. 100

Objectives Students would be able to: u. Determine the end behavior of the graph of even and odd degree power function. u Use graphs and algebraic functions to determine symmetry of even and odd functions. u. Determine algebraically whether a function is even, odd, or neither Mastery is evidenced by scoring a 3 out of 4 on the Exit Slip

Common Core Standards 4. Interpret functions that arise in applications in terms of the context. 7. Analyze functions using different representations.

What is a Power Function? A power function is a function of the form where n is a nonnegative integer.

Patterns in Power Functions Textbook page 335 v. Odd degree functions point up and down. Even degree functions point up only. The greater the degree of the function, the more flat the graph is near the origin. v. Power functions raised to an odd degree moves up from left to right, flattening near the origin, depending on the power. v. Power functions raised up to an even degree concave up parabola, flattening near the origin, depending on the power.

Textbook page 335

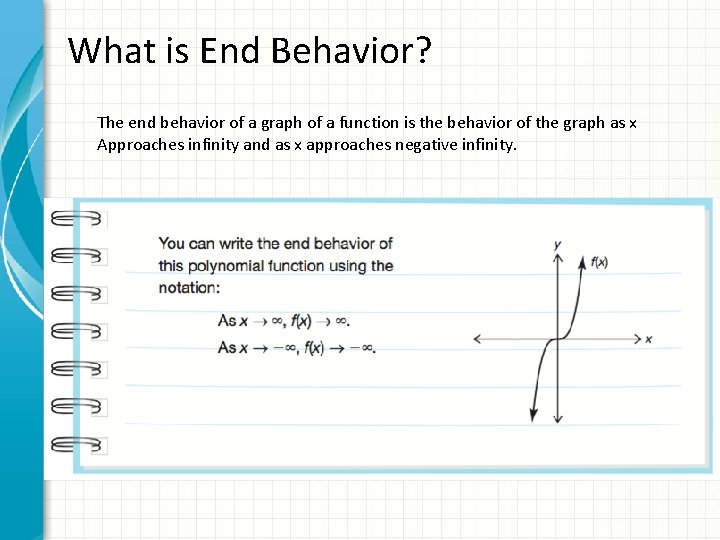
What is End Behavior? The end behavior of a graph of a function is the behavior of the graph as x Approaches infinity and as x approaches negative infinity.

To describe the end behavior of any polynomial function (textbook page 337)

Symmetry About a Line Symmetry About a Point If a graph is symmetric about a line, the line divides the graph into two identical parts. When the line of symmetry is the yaxis then the function is even A function is symmetric about a point if each point on the graph has a point the same distance from the central point, but in the opposite direction. Special attention is given when the central point is the origin as it determines that the function is odd.

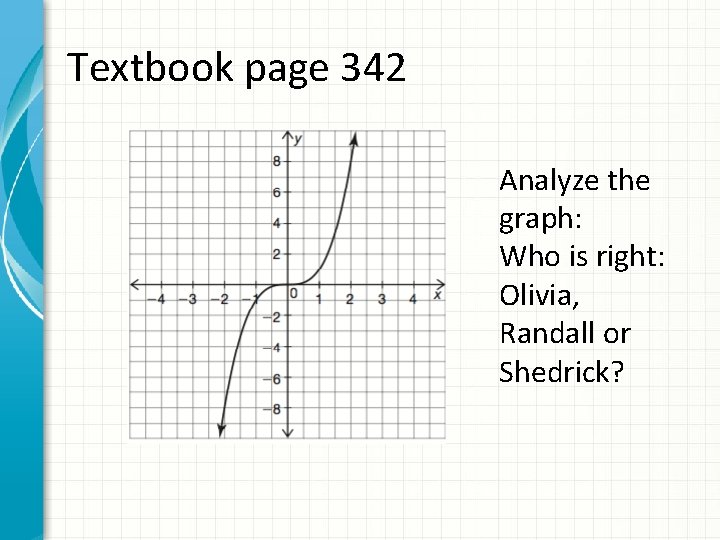
Textbook page 342 Analyze the graph: Who is right: Olivia, Randall or Shedrick?

Think about point of symmetry about the origin as a double reflection:

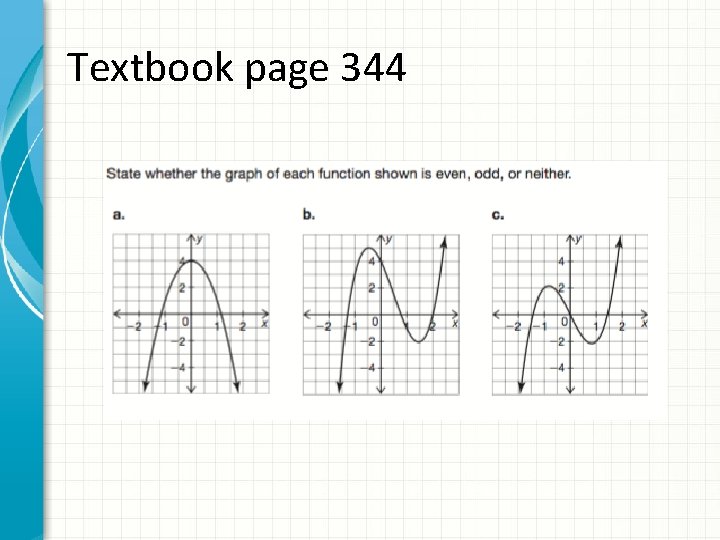
Textbook page 344

How to determine if the function is even or odd algebraically? An even function has a graph symmetric about the y-axis, thus: An odd function has a graph symmetric about the origin, thus:

Determine whether the functions are even, odd, or neither: (textbook page 346)