Unit 5 Logarithmic Functions Inverse of exponential functions




![Useful Log Properties: MEMORIZE THEM!!! Exponential Reasoning [1] [2] [3] [4] [5] Cannot take Useful Log Properties: MEMORIZE THEM!!! Exponential Reasoning [1] [2] [3] [4] [5] Cannot take](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-5.jpg)

![Useful Log Properties: Examples [1] [2] [3] [5] Useful Log Properties: Examples [1] [2] [3] [5]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-7.jpg)




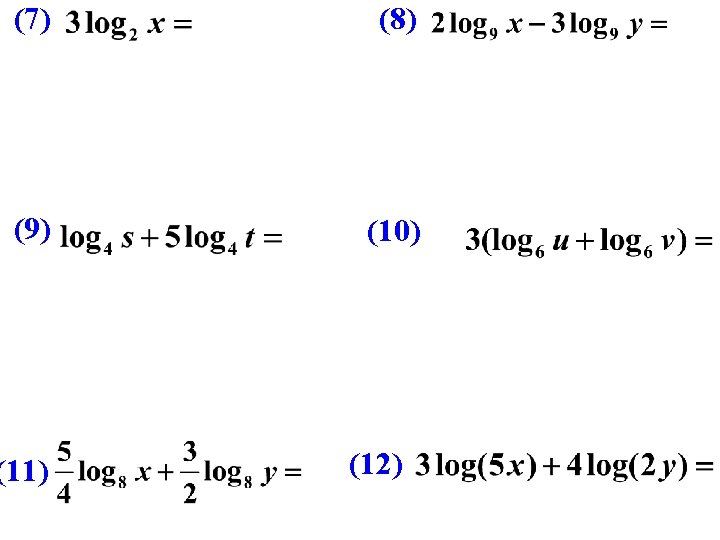
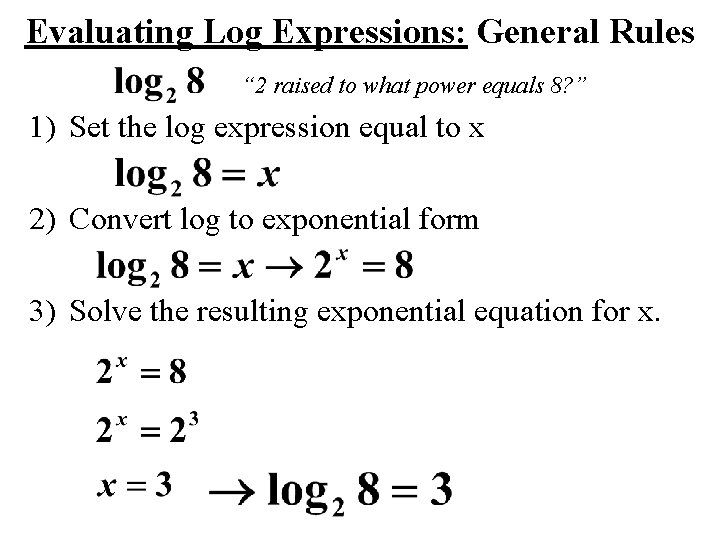

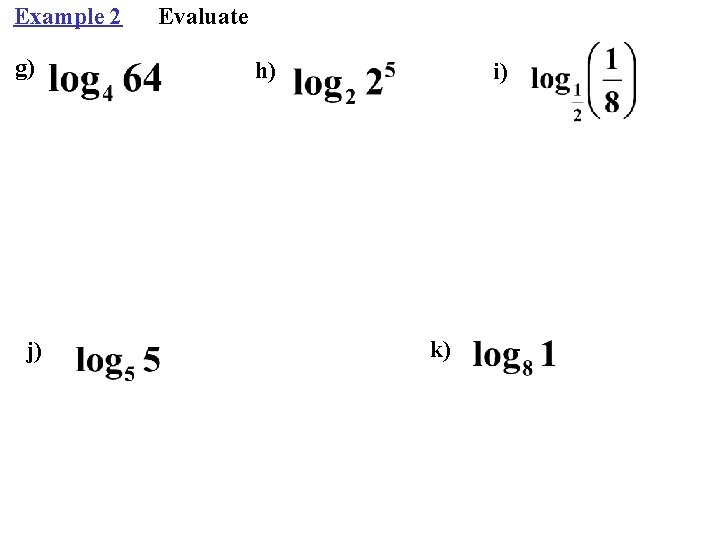


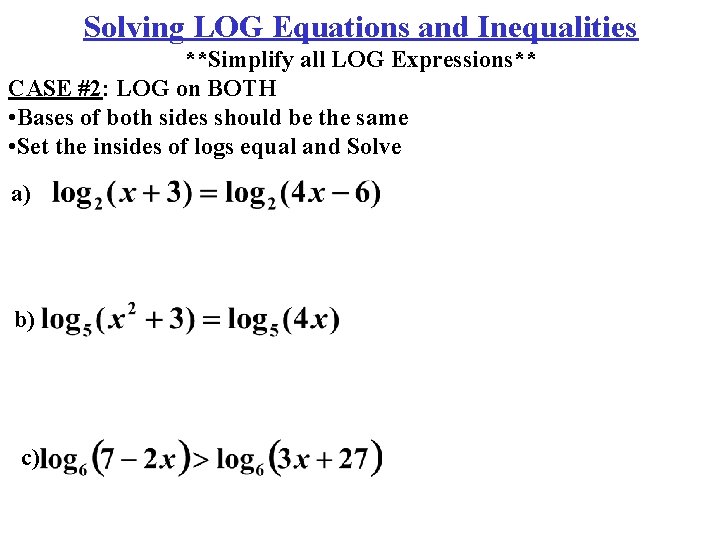




![APPLYING LOG PROPERTIES: SOLVING with PRODUCT PROPERTY [a] [b] APPLYING LOG PROPERTIES: SOLVING with PRODUCT PROPERTY [a] [b]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-23.jpg)
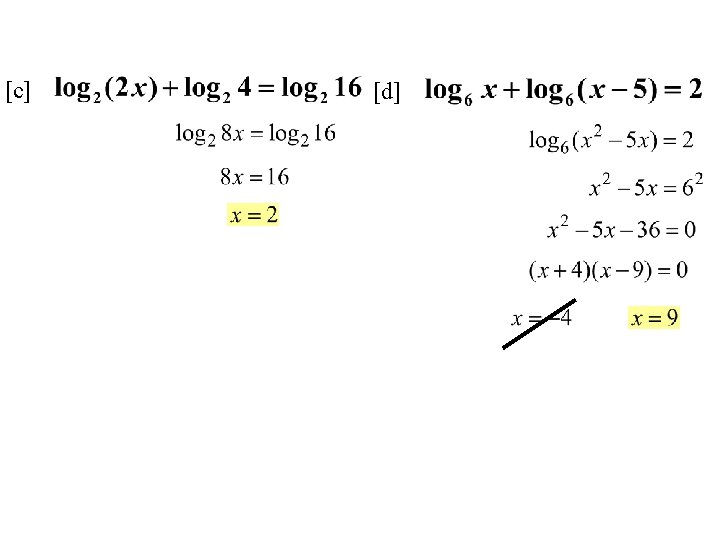
![APPLYING LOG PROPERTIES: SOLVING with QUOTIENT PROPERTY [a] [b] APPLYING LOG PROPERTIES: SOLVING with QUOTIENT PROPERTY [a] [b]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-25.jpg)
![APPLYING LOG PROPERTIES: SOLVING with POWER PROPERTY [a] [b] APPLYING LOG PROPERTIES: SOLVING with POWER PROPERTY [a] [b]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-26.jpg)
![GENERAL PRACTICE [a] [c] [b] [d] GENERAL PRACTICE [a] [c] [b] [d]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-27.jpg)
![GENERAL PRACTICE: Continued [e] [f] GENERAL PRACTICE: Continued [e] [f]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-28.jpg)
- Slides: 28

Unit 5: Logarithmic Functions Inverse of exponential functions. “log base b of x” “base b to x power” • Domain: x > 0 • Domain: all real numbers • Range: y > 0 Ex 1: Ex 2: “log base 2 of 6” “log base 7 of 12”

Logarithmic and Exponential Conversions (1) Base is always the base (2) Exponent and Answer switch Convert each log expression into an exponential expression. 1. 2. 3. Convert each exponential expression into a log expression. 4. 5. 6.

Example 1 CONVERSION PRACTICE Exponential Logarithmic a) _________ b) _________ c) _______ d) _______ f) f) __________________

Example 1: Continued (Fill In The Blanks) Exponential Logarithmic a) _________ b) _______ c) _________ d) _______ e) f) __________________
![Useful Log Properties MEMORIZE THEM Exponential Reasoning 1 2 3 4 5 Cannot take Useful Log Properties: MEMORIZE THEM!!! Exponential Reasoning [1] [2] [3] [4] [5] Cannot take](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-5.jpg)
Useful Log Properties: MEMORIZE THEM!!! Exponential Reasoning [1] [2] [3] [4] [5] Cannot take logs of negative number “change of base formula” (for calculator)

OPERATION PROPERTIES OF LOGARITHMS #1) Product Property: Log of a product is equal to the SUM of the logs of both multipliers of the same base #2) Quotient Property: Log of a quotient “fraction” is equal to the DIFFERENCE of the logs of the numerator and denominator #3) Power Property: Log of a power statement is equal to the MULTIPLICATION of the power (p) times the log of the
![Useful Log Properties Examples 1 2 3 5 Useful Log Properties: Examples [1] [2] [3] [5]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-7.jpg)
Useful Log Properties: Examples [1] [2] [3] [5]

OPERATION PROPERTIES OF LOGARITHMS Condense Expand (1 a) (1 b) (2 a) (2 b) (3 a) (3 b)

Expand Each Logarithm Using Properties (2) (3) (1) (4) (5) (6)

Expand Each Logarithm Using Properties (7) (10) (8) (9) (11)

Condense Each Logarithm Using Properties (2) (1) (3) (4) (5) (6)
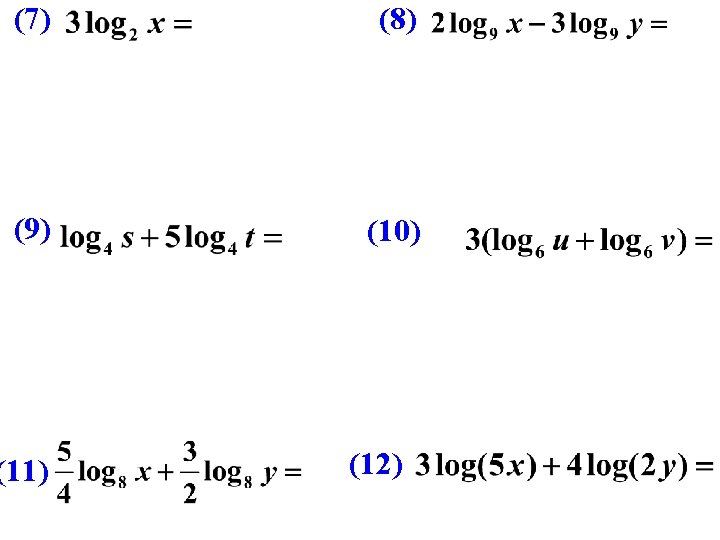
(7) (8) (9) (10) (11) (12)
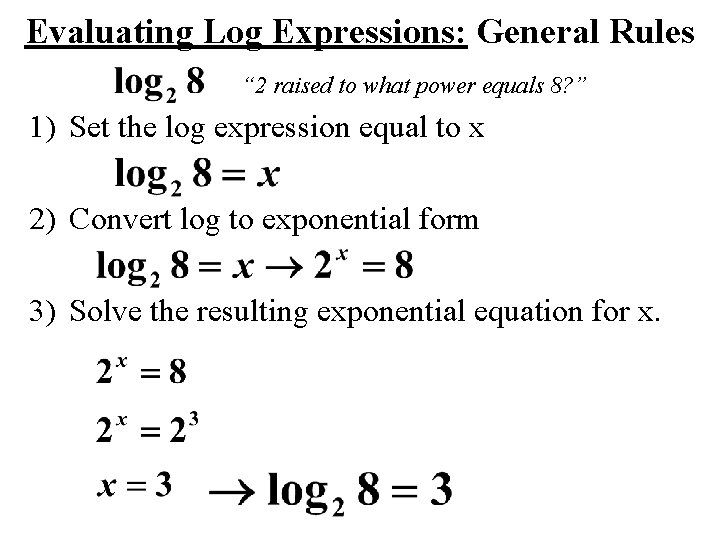
Evaluating Log Expressions: General Rules “ 2 raised to what power equals 8? ” 1) Set the log expression equal to x 2) Convert log to exponential form 3) Solve the resulting exponential equation for x.

Example 2 a) d) Evaluate using properties b) e) c) f)
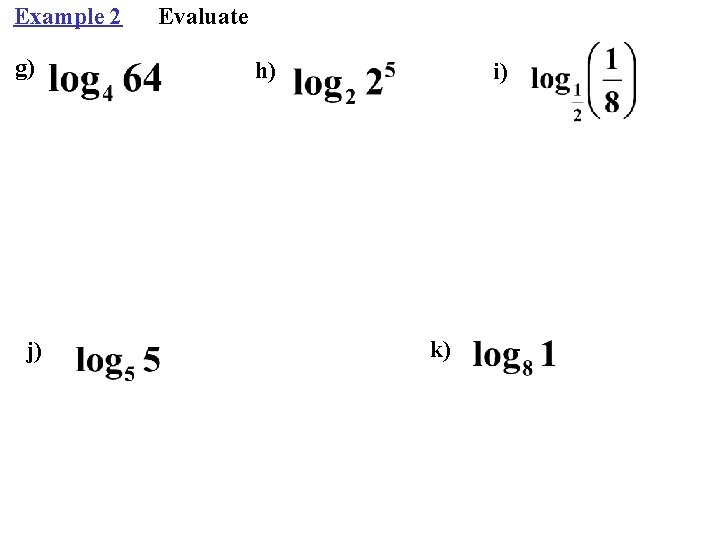
Example 2 g) j) Evaluate h) i) k)

Solve Exponential Equations with Logs • Solve the exponential until form, bx = a. • Clearing Bases Using Log Conversion • Some answers cannot be evaluated by hand require calculator a) b)

Solving LOG Equations and Inequalities **SIMPLIFY all LOG Expressions** CASE #1: LOG on one side and VALUE on other Side • Apply Exponential Conversion • Solve (For inequalities x < # requires 0 < x < # because of domain a) b) c) d)
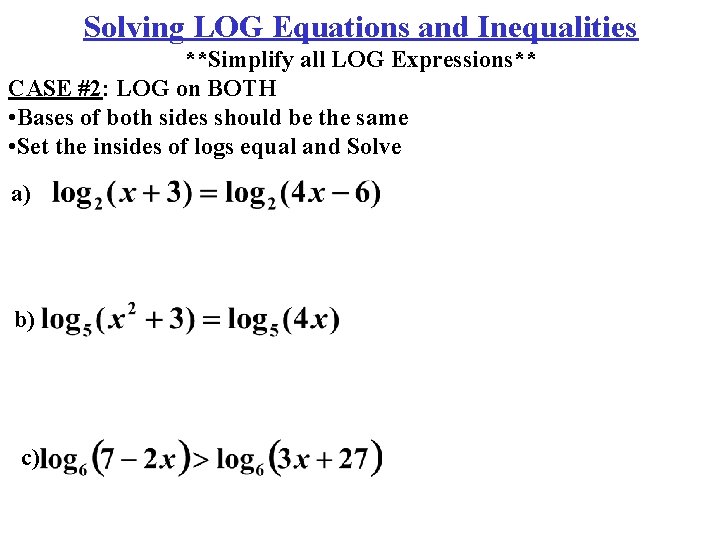
Solving LOG Equations and Inequalities **Simplify all LOG Expressions** CASE #2: LOG on BOTH • Bases of both sides should be the same • Set the insides of logs equal and Solve a) b) c)

Practice: Solving Log Equations – by hand 1. 3. 2. 4.

Practice: Solving Log Equations w/ CALC 5. 6.

Log Property Practice • Condense each Log Expression 1. 3. 2.

Use the given values and log properties to evaluate 4. 5. 6. 7. 8.
![APPLYING LOG PROPERTIES SOLVING with PRODUCT PROPERTY a b APPLYING LOG PROPERTIES: SOLVING with PRODUCT PROPERTY [a] [b]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-23.jpg)
APPLYING LOG PROPERTIES: SOLVING with PRODUCT PROPERTY [a] [b]
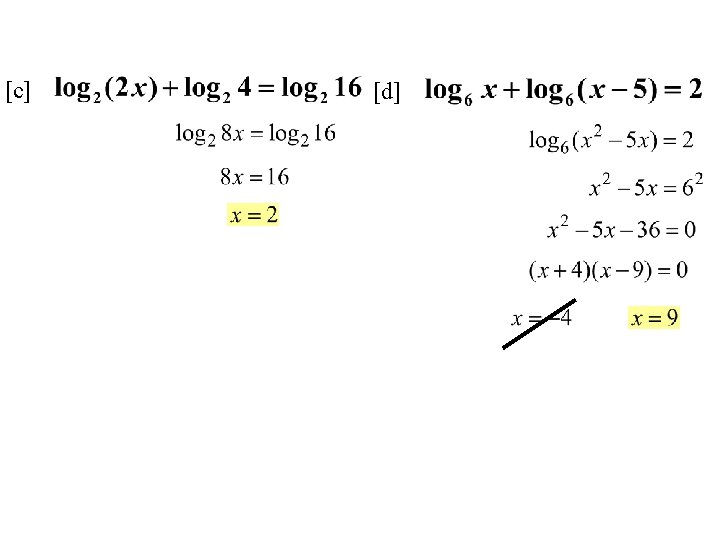
![APPLYING LOG PROPERTIES SOLVING with QUOTIENT PROPERTY a b APPLYING LOG PROPERTIES: SOLVING with QUOTIENT PROPERTY [a] [b]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-25.jpg)
APPLYING LOG PROPERTIES: SOLVING with QUOTIENT PROPERTY [a] [b]
![APPLYING LOG PROPERTIES SOLVING with POWER PROPERTY a b APPLYING LOG PROPERTIES: SOLVING with POWER PROPERTY [a] [b]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-26.jpg)
APPLYING LOG PROPERTIES: SOLVING with POWER PROPERTY [a] [b]
![GENERAL PRACTICE a c b d GENERAL PRACTICE [a] [c] [b] [d]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-27.jpg)
GENERAL PRACTICE [a] [c] [b] [d]
![GENERAL PRACTICE Continued e f GENERAL PRACTICE: Continued [e] [f]](https://slidetodoc.com/presentation_image_h/81979169e9ce4e023e744d5e68c11246/image-28.jpg)
GENERAL PRACTICE: Continued [e] [f]