Unit 5 Greedy Algorithm Gopi Sanghani 97277 47317

Unit – 5 Greedy Algorithm Gopi Sanghani � 97277 -47317 �gopi. sanghani@darshan. ac. in Analysis and Design of Algorithm (2150703) Darshan Institute of Engineering & Technology

Topics to be Covered § General Characteristics of greedy algorithms § Elements of Greedy Strategy § Make change Problem § Minimum Spanning trees (Kruskal’s algorithm, Prim’s algorithm) § The Knapsack Problem § Job Scheduling Problem § Huffman code. Greedy Algorithm 2 Darshan Institute of Engineering & Technology

Introduction § A greedy algorithm always makes the choice that seems to be the best at that moment. § it never reconsiders this decision. § E. g. , • Get the best possible dress from a shop for yourself. Greedy Algorithm 3 Darshan Institute of Engineering & Technology

Characteristics of Greedy Algorithms § Greedy Algorithm 4 Darshan Institute of Engineering & Technology

Elements of Greedy Strategy § The greedy algorithm consists of four functions. 1. Solution Function: - A function that checks whether chosen set of items provides a solution. 2. Feasible Function: - A function that checks the feasibility of a set. 3. Selection Function: - The selection function tells which of the candidates is the most promising. 4. Objective Function: - An objective function, which does not appear explicitly, but gives the value of a solution. Greedy Algorithm 5 Darshan Institute of Engineering & Technology

Make Change Problem § Greedy Algorithm 6 Darshan Institute of Engineering & Technology

Make Change Problem § Amount Selected coins are, coins quantity 10 2 5 1 2 1 1 1 Greedy Algorithm 28 27 25 20 0 Total required coins = 5 Selected coins = {10, 5, 2, 1} 7 Darshan Institute of Engineering & Technology

Make Change - Algorithm # Input: C = {10, 5, 2, 1, 0. 5} //C is a candidate set # Output: S: set of selected coins Function make-change(n): set of coins S ← Ø {S is a set that will hold the solution} sum ← 0 {sum of the items in solution set S} while sum ≠ n do x ← the largest item in C such that sum + x ≤ n if there is no such item then return "no solution found" S ← S U {a coin of value x) sum ← sum + x return S] ← A[j+1] A[temp Greedy Algorithm 8 Darshan Institute of Engineering & Technology

Make Change – The Greedy Property § 5 4 3 The minimum coins required are Greedy Algorithm 9 2 Darshan Institute of Engineering & Technology

MINIMUM SPANNING TREE 10

Minimum Spanning Tree (MST) § Greedy Algorithm 11 Darshan Institute of Engineering & Technology

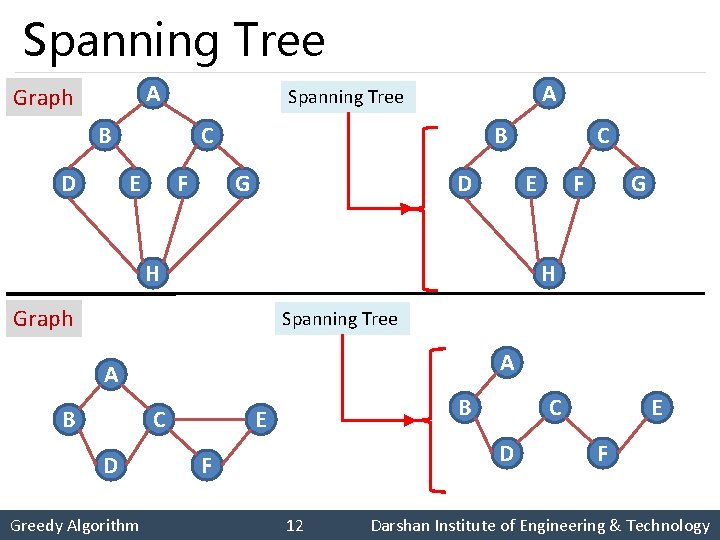
Spanning Tree A Graph B D A Spanning Tree C E F B G D C E H F G H Graph Spanning Tree A A B C D Greedy Algorithm B E C D F 12 E F Darshan Institute of Engineering & Technology

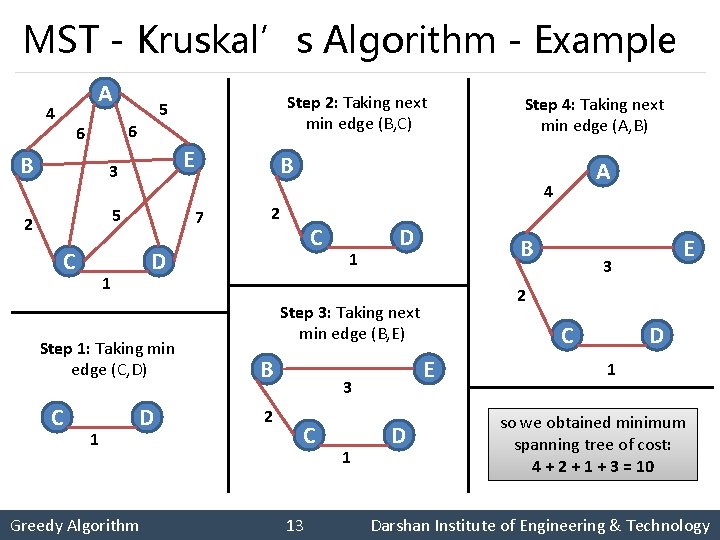
MST - Kruskal’s Algorithm - Example A 4 6 6 B E 3 5 2 C 1 D 2 C Greedy Algorithm 1 D B B C 13 1 D 3 C E 3 E 2 Step 3: Taking next min edge (B, E) 2 A 4 D 1 Step 4: Taking next min edge (A, B) B 7 Step 1: Taking min edge (C, D) C Step 2: Taking next min edge (B, C) 5 D 1 so we obtained minimum spanning tree of cost: 4 + 2 + 1 + 3 = 10 Darshan Institute of Engineering & Technology

Kruskal’s Algorithm Function Kruskal(G = (N, A)) Sort A by increasing length n ← the number of nodes in N T ← Ø {edges of the minimum spanning tree} Define n sets, containing a different element of set N repeat e ← {u, v} //e is the shortest edge not yet considered find(u) tells, node u is found in ucomp ← find(u) which connected component vcomp ← find(v) if ucomp ≠ vcomp then merge(ucomp, vcomp) T ← T U {e} merge(ucomp, vcomp) is used to merge two connected components. until T contains n - 1 edges return T Greedy Algorithm 14 Darshan Institute of Engineering & Technology

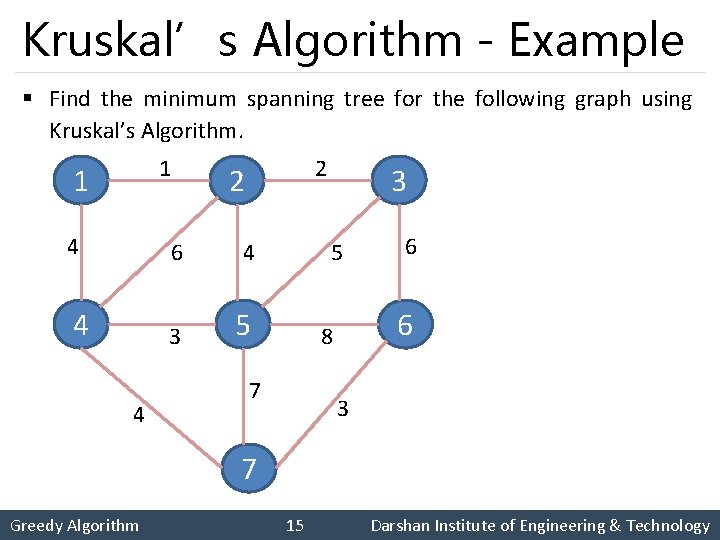
Kruskal’s Algorithm - Example § Find the minimum spanning tree for the following graph using Kruskal’s Algorithm. 1 1 2 2 4 6 4 4 3 5 6 8 7 6 3 7 Greedy Algorithm 15 Darshan Institute of Engineering & Technology

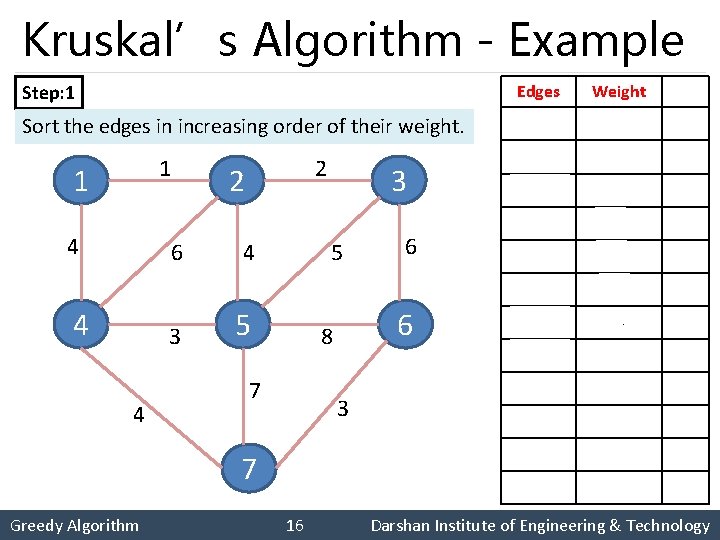
Kruskal’s Algorithm - Example Step: 1 Edges Weight Sort the edges in increasing order of their weight. {1, 2} 1 {2, 3} 2 {4, 5} 3 {6, 7} 3 {1, 4} 4 {2, 5} 4 {4, 7} 4 {3, 5) 5 {2, 4} 6 {3, 6} 6 {5, 7} 7 {5, 6} 8 1 1 4 6 4 3 4 2 2 4 5 5 7 3 16 6 6 8 7 Greedy Algorithm 3 Darshan Institute of Engineering & Technology

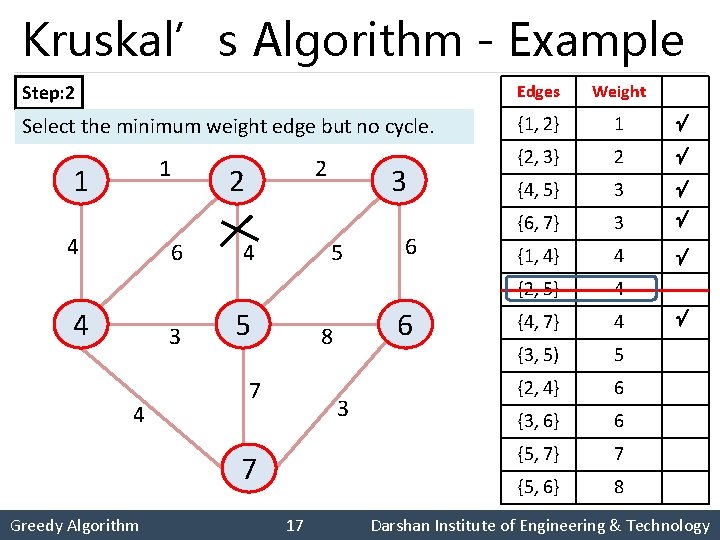
Kruskal’s Algorithm - Example Step: 2 Edges Weight Select the minimum weight edge but no cycle. {1, 2} 1 {2, 3} 2 {4, 5} 3 {6, 7} 3 {1, 4} 4 {2, 5} 4 {4, 7} 4 {3, 5) 5 {2, 4} 6 {3, 6} 6 {5, 7} 7 {5, 6} 8 1 1 4 6 4 3 4 2 2 4 5 5 7 3 17 6 6 8 7 Greedy Algorithm 3 Darshan Institute of Engineering & Technology

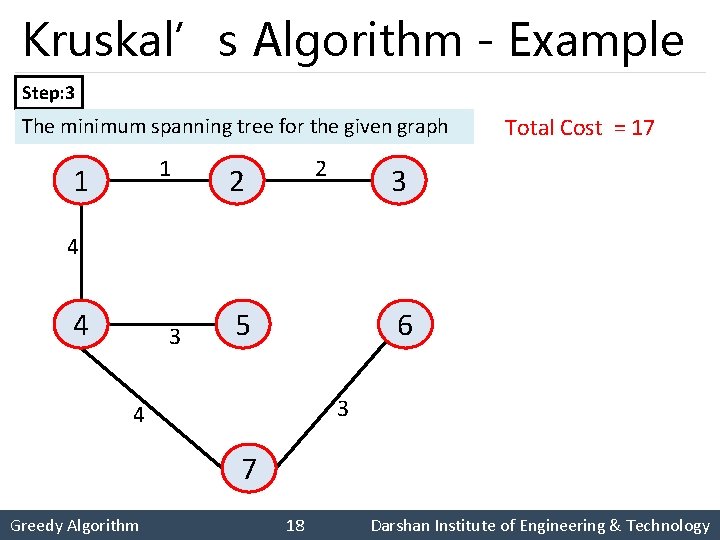
Kruskal’s Algorithm - Example Step: 3 The minimum spanning tree for the given graph 1 1 2 2 Total Cost = 17 3 4 4 3 5 6 3 4 7 Greedy Algorithm 18 Darshan Institute of Engineering & Technology

Kruskal’s Algorithm - Example Step Edges considered - {u, v} Connected Components Init. - {1} {2} {3} {4} {5} {6} {7} 1 2 3 4 5 6 7 {1, 2} {2, 3} {4, 5} {6, 7} {1, 4} {2, 5} {4, 7} {1, 2} (3} {4} {5} {6} {7} {1, 2, 3} {4, 5} {6, 7} {1, 2, 3, 4, 5} {6, 7} Rejected {1, 2, 3, 4, 5, 6, 7} Greedy Algorithm 19 Edges Weight {1, 2} 1 {2, 3} 2 {4, 5} 3 {6, 7} {1, 4} {2, 5} {4, 7} 3 4 4 4 Total Cost = 17 Darshan Institute of Engineering & Technology

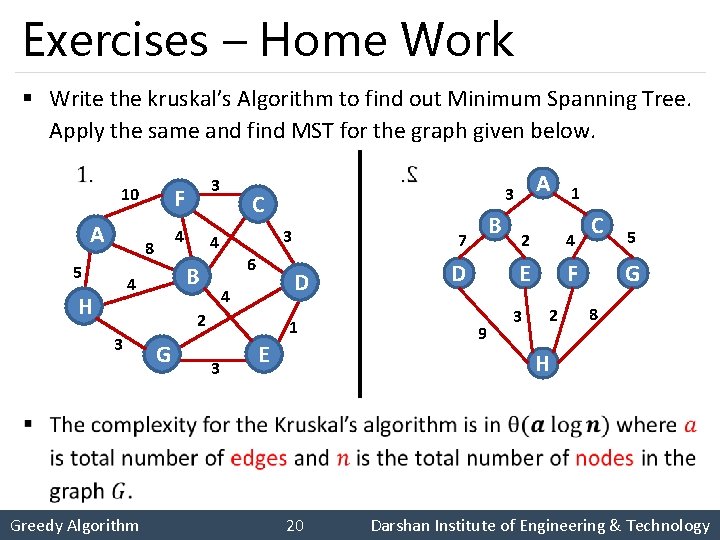
Exercises – Home Work § Write the kruskal’s Algorithm to find out Minimum Spanning Tree. Apply the same and find MST for the graph given below. A 4 8 5 3 6 2 3 Greedy Algorithm G 1 3 B 7 D 4 A 3 C 4 B 4 H 3 F 10 E D 9 1 2 4 E F 3 2 C 5 G 8 H 20 Darshan Institute of Engineering & Technology

Prim’s Algorithm § Greedy Algorithm 21 Darshan Institute of Engineering & Technology

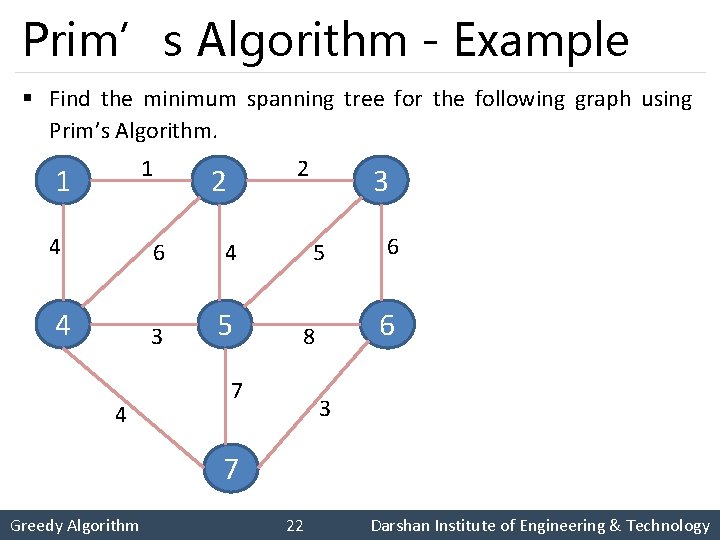
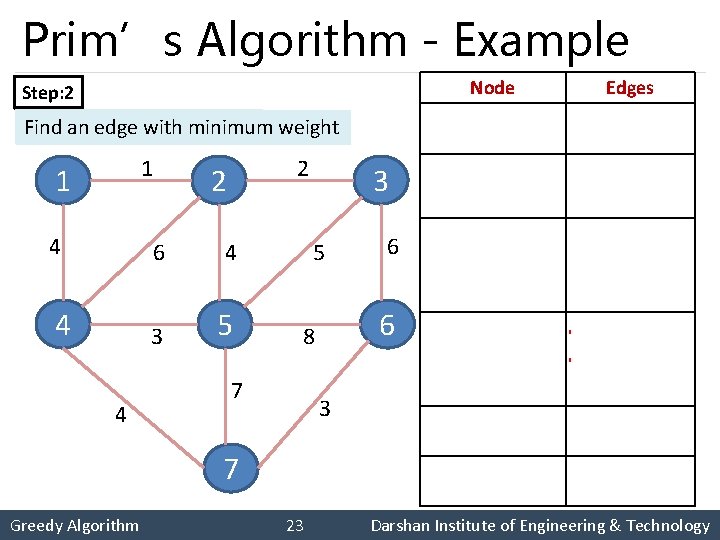
Prim’s Algorithm - Example § Find the minimum spanning tree for the following graph using Prim’s Algorithm. 1 1 2 2 4 6 4 4 3 5 6 8 7 6 3 7 Greedy Algorithm 22 Darshan Institute of Engineering & Technology

Prim’s Algorithm - Example Node Step: 2 Step: 1 Select arbitrary node. weight Find anany edge with minimum 1 1 2 2 4 6 4 4 3 5 4 5 7 6 6 8 3 7 Greedy Algorithm 3 Edges 1 {1, 2}, {1, 4} 1, 2 {1, 4}, {2, 3} {2, 4}, {2, 5} 1, 2, 3 {1, 4}, {2, 5}, {3, 6} {2, 4} {2, 5} {3, 6} {4, 5} {4, 7} 1, 2, 3, 4, 5, 6 {6, 7} 23 Darshan Institute of Engineering & Technology

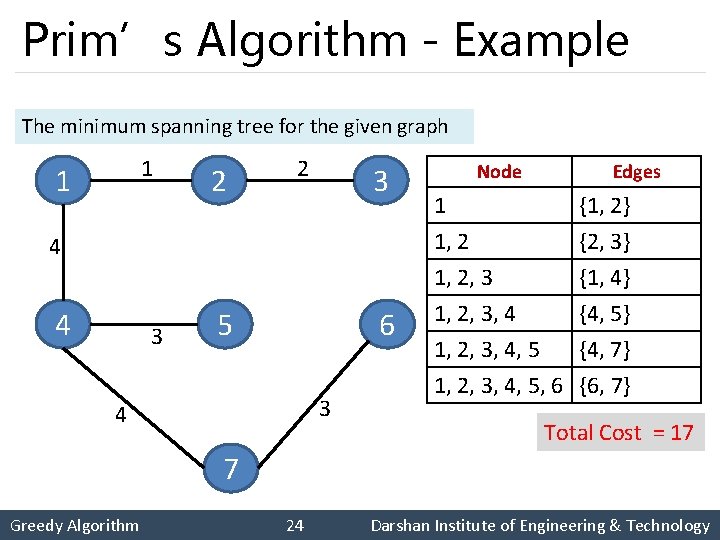
Prim’s Algorithm - Example The minimum spanning tree for the given graph 1 1 2 2 3 4 4 3 5 6 3 4 Node Edges 1 {1, 2} 1, 2, 3, 4, 5 {2, 3} {1, 4} {4, 5} {4, 7} 1, 2, 3, 4, 5, 6 {6, 7} Total Cost = 17 7 Greedy Algorithm 24 Darshan Institute of Engineering & Technology

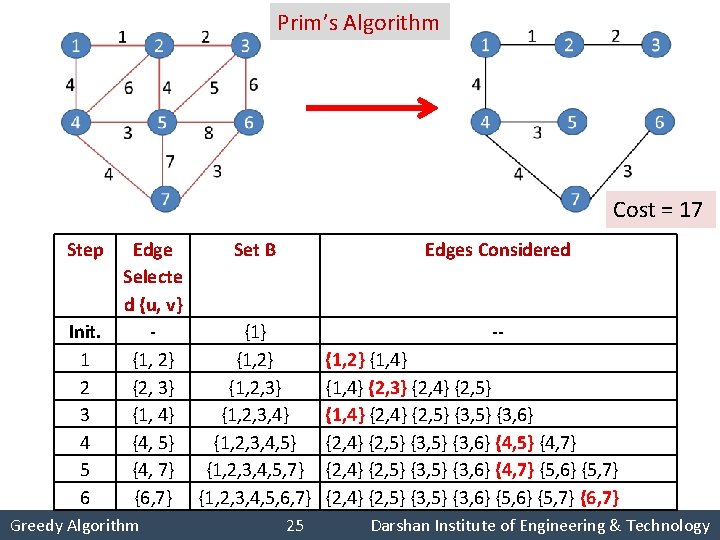
Prim’s Algorithm Cost = 17 Step Init. 1 2 3 4 5 6 Edge Set B Selecte d {u, v} {1, 2} {2, 3} {1, 4} {1, 2, 3, 4} {4, 5} {1, 2, 3, 4, 5} {4, 7} {1, 2, 3, 4, 5, 7} {6, 7} {1, 2, 3, 4, 5, 6, 7} Greedy Algorithm 25 Edges Considered -{1, 2} {1, 4} {2, 3} {2, 4} {2, 5} {1, 4} {2, 5} {3, 6} {2, 4} {2, 5} {3, 6} {4, 5} {4, 7} {2, 4} {2, 5} {3, 6} {4, 7} {5, 6} {5, 7} {2, 4} {2, 5} {3, 6} {5, 7} {6, 7} Darshan Institute of Engineering & Technology

Prim’s Algorithm § Greedy Algorithm 26 Darshan Institute of Engineering & Technology

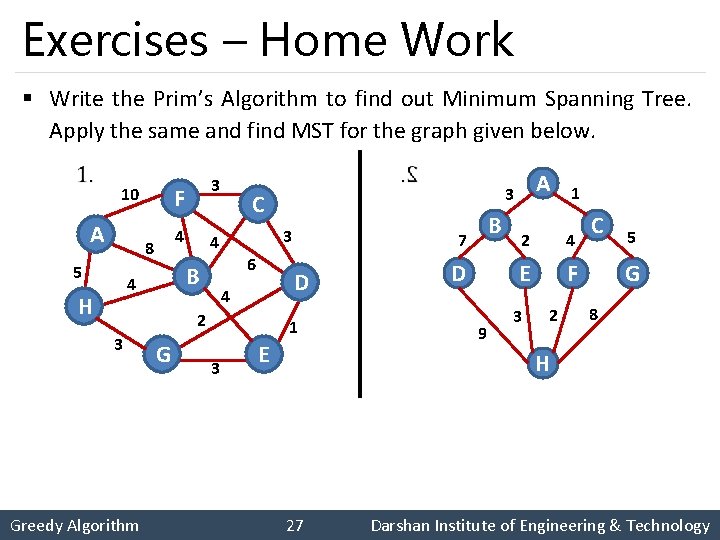
Exercises – Home Work § Write the Prim’s Algorithm to find out Minimum Spanning Tree. Apply the same and find MST for the graph given below. A 4 8 5 3 6 2 3 Greedy Algorithm G 1 3 B 7 D 4 A 3 C 4 B 4 H 3 F 10 E D 9 1 2 4 E F 3 2 C 5 G 8 H 27 Darshan Institute of Engineering & Technology

SINGLE SOURCE SHORTEST PATH 28

Dijkstra’s Algorithm § Greedy Algorithm 29 Darshan Institute of Engineering & Technology

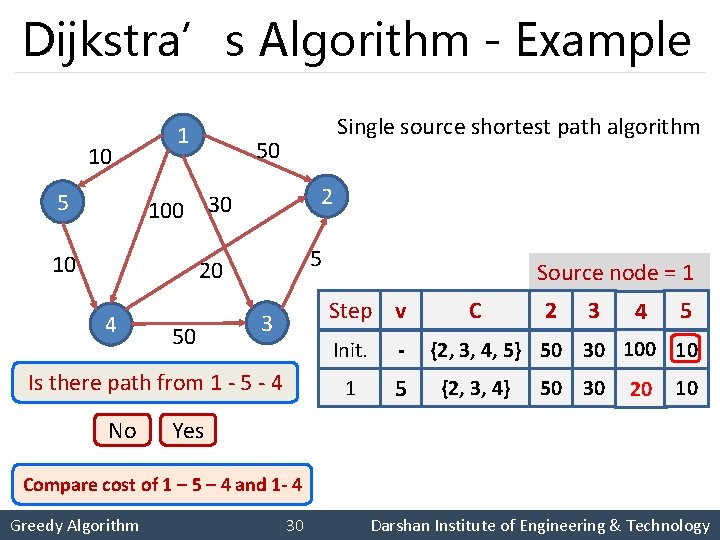
Dijkstra’s Algorithm - Example 10 5 1 Single source shortest path algorithm 50 2 100 30 10 5 20 4 50 Step v 3 Is there path from 1 - 5 - 4 2 3 No Source node = 1 Init. - 1 5 C 2 3 4 5 {2, 3, 4, 5} 50 30 10 {2, 3, 4} 50 30 20 10 Yes Compare cost of 1 – 5 – 4 and 1 - 4 Greedy Algorithm 30 Darshan Institute of Engineering & Technology

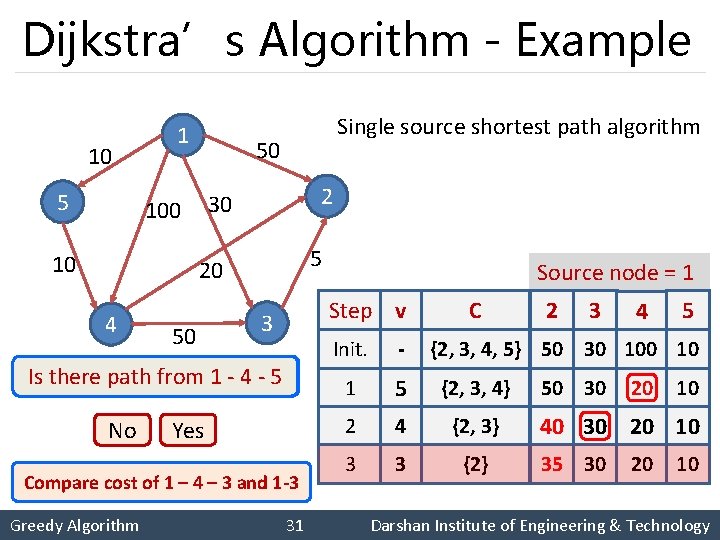
Dijkstra’s Algorithm - Example 10 5 1 50 2 30 10 Single source shortest path algorithm 5 20 4 50 Step v 3 Is there path from 1 - 4 - 5 23 No Yes Compare cost of 1 – 4 – 3 2 and 1 -3 1 -2 Greedy Algorithm Source node = 1 31 C Init. - 1 5 {2, 3, 4} 2 4 {2, 3} 3 3 {2} 2 3 4 5 {2, 3, 4, 5} 50 30 10 50 30 20 10 40 30 20 10 35 30 20 10 Darshan Institute of Engineering & Technology

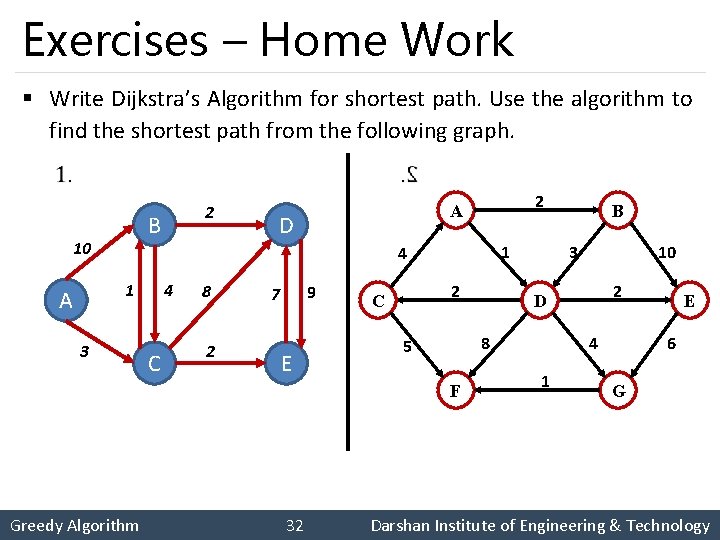
Exercises – Home Work § Write Dijkstra’s Algorithm for shortest path. Use the algorithm to find the shortest path from the following graph. B 10 2 A D 1 4 1 A 2 3 4 C 8 2 9 7 E 2 C F Greedy Algorithm 32 3 10 2 D 8 5 B 4 1 E 6 G Darshan Institute of Engineering & Technology

Dijkstra’s Algorithm § Greedy Algorithm 33 Darshan Institute of Engineering & Technology

FRACTIONAL KNAPSACK PROBLEM 34

Fractional Knapsack Problem § Greedy Algorithm 35 Darshan Institute of Engineering & Technology

Fractional Knapsack Problem § Greedy Algorithm 36 Darshan Institute of Engineering & Technology

Fractional Knapsack Problem - Example § Greedy Algorithm 37 Darshan Institute of Engineering & Technology

Greedy Solution § Three selection functions can be defined as, 1. Sort the items in descending order of their values and select the items till weight criteria is satisfied. 2. Sort the items in ascending order of their weight and select the items till weight criteria is satisfied. 3. To calculate the ratio value/weight for each item and sort the item on basis of this ratio. Then take the item with the highest ratio and add it. Greedy Algorithm 38 Darshan Institute of Engineering & Technology

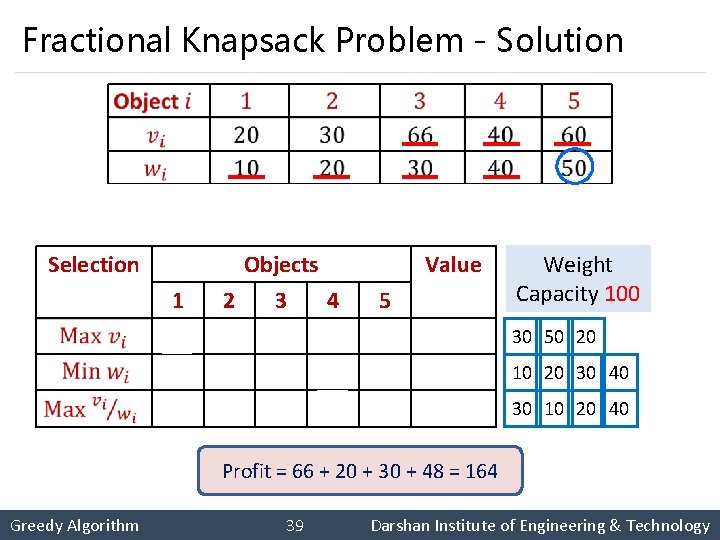
Fractional Knapsack Problem - Solution 2. 0 Selection 1. 5 1 0 1 Objects 2 3 4 0 1 0. 5 1 1 1 0 2. 2 1. 0 Value 1. 2 Weight Capacity 100 5 1 0 146 156 30 50 20 0. 8 164 30 10 20 40 10 20 30 40 Profit==66 66 20 30 48 Profit 20++60 30++(40 66 *+ 0. 5) 40 ==164 156 146 Greedy Algorithm 39 Darshan Institute of Engineering & Technology

Fractional Knapsack Problem - Algorithm § (100 – 60) / 50 = 0. 8 Greedy Algorithm 40 Darshan Institute of Engineering & Technology

Exercises – Home Work § Greedy Algorithm 41 Darshan Institute of Engineering & Technology

ACTIVITY SELECTION PROBLEM 42

Activity Selection Problem § Greedy Algorithm 43 Darshan Institute of Engineering & Technology

Activity Selection Problem - Example § Greedy Algorithm 44 Sr. Activity 1 P (1, 4) 2 Q (3, 5) 3 R (0, 6) 4 S (5, 7) 5 T (3, 8) 6 U (5, 9) 7 V (6, 10) 8 W (8, 11) 9 X (8, 12) 10 Y (2, 13) 11 Z (12, 14) Darshan Institute of Engineering & Technology

Activity Selection Problem - Example § Solution: Sr. Activity 1. A = {P} 1 P (1, 4) 2. A = {P, S} 2 Q (3, 5) 3. A = {P, S, W} 3 R (0, 6) 4 S (5, 7) 5 T (3, 8) 6 U (5, 9) 7 V (6, 10) 8 W (8, 11) 9 X (8, 12) 10 Y (2, 13) 11 Z (12, 14) 4. A = {P, S, W, Z} Answer: A = {P, S, W, Z} Greedy Algorithm 45 Darshan Institute of Engineering & Technology

Activity Selection - Algorithm: Activity Selection Step I: Sort the input activities by increasing finishing time. f 1 ≤ f 2 ≤. . . ≤ fn Step II: Call GREEDY-ACTIVITY-SELECTOR (s, f) n = length [s] A = {i} j = 1 for i = 2 to n do if s i ≥ fj then A = A U {i} j = i return set A Greedy Algorithm 46 Darshan Institute of Engineering & Technology

Exercises - HW 1. Given arrival and departure times of all trains that reach a railway station, find the minimum number of platforms required for the railway station so that no train waits. We are given two arrays which represent arrival and departure times of trains that stop. Arr[] = {9: 00, 9: 40, 9: 50, 11: 00, 15: 00, 18: 00} dep[] = {9: 10, 12: 00, 11: 20, 11: 30, 19: 00, 20: 00} Greedy Algorithm 47 Darshan Institute of Engineering & Technology

JOB SCHEDULING WITH DEADLINES 48

Job Scheduling with Deadlines § Greedy Algorithm 49 Darshan Institute of Engineering & Technology

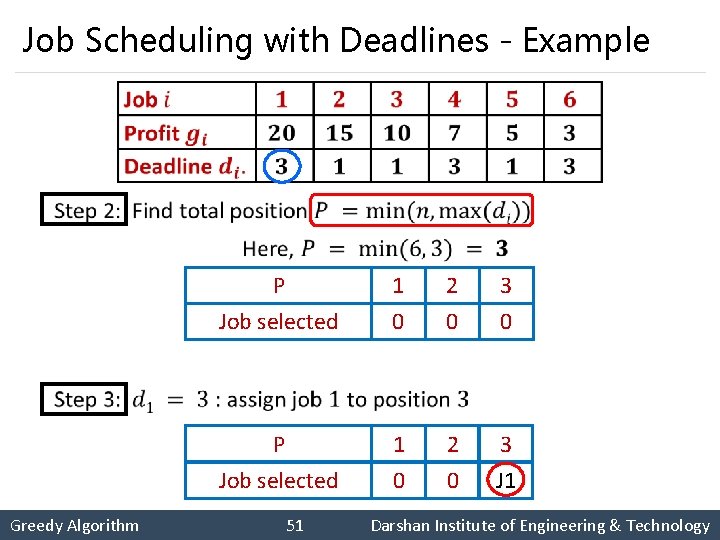
Job Scheduling with Deadlines - Example § Greedy Algorithm 50 Darshan Institute of Engineering & Technology

Job Scheduling with Deadlines - Example § Greedy Algorithm P 1 2 3 Job selected 0 0 0 P 1 2 3 Job selected 0 0 J 1 51 Darshan Institute of Engineering & Technology

Job Scheduling with Deadlines - Example § P 1 2 3 Job selected J 2 0 J 1 Position 1 is already occupied, so reject job 3 Greedy Algorithm 52 Darshan Institute of Engineering & Technology

Job Scheduling with Deadlines - Example § Greedy Algorithm P 1 2 3 Job selected J 2 J 4 J 1 53 Darshan Institute of Engineering & Technology

Exercises – Home Work 1. Using greedy algorithm find an optimal schedule for following jobs with �� =4. Profits: (a, b, c, d) = (20, 10, 40, 30) & Deadline: (d 1, d 2, d 3, d 4) = (4, 1, 1, 1) 2. Using greedy algorithm find an optimal schedule for following jobs with �� =5. Profits: (a, b, c, d, e) = (100, 19, 27, 25, 15) & Deadline: (d 1, d 2, d 3, d 4, d 5) = (2, 1, 3) Greedy Algorithm 54 Darshan Institute of Engineering & Technology

HUFFMAN CODES 56

Huffman Codes § Huffman invented a greedy algorithm that constructs an optimal prefix code called a Huffman code. § Huffman coding is a lossless data compression algorithm. § It assigns variable-length codes to input characters. § Lengths of the assigned codes are based on the frequencies of corresponding characters. § The most frequent character gets the smallest code and the least frequent character gets the largest code. § The variable-length codes assigned to input characters are Prefix Codes. Greedy Algorithm 57 Darshan Institute of Engineering & Technology

Huffman Codes § In Prefix codes, the codes are assigned in such a way that the code assigned to one character is not a prefix of code assigned to any other character. § For example, § a = 01, b = 010 and c = 11 Not a prefix code § This is how Huffman Coding makes sure that there is no ambiguity when decoding the generated bit stream. § There are mainly two major parts in Huffman Coding 1. Build a Huffman Tree from input characters. 2. Traverse the Huffman Tree and assign codes to characters. Greedy Algorithm 58 Darshan Institute of Engineering & Technology

Huffman Codes - Example § Find the Huffman codes for the following characters. Characters Frequency (in thousand) a b c d e f 45 13 12 16 9 5 Step 1: Arrange the characters in the Ascending order of their frequency. f: 5 Greedy Algorithm e: 9 c: 12 59 b: 13 d: 16 a: 45 Darshan Institute of Engineering & Technology

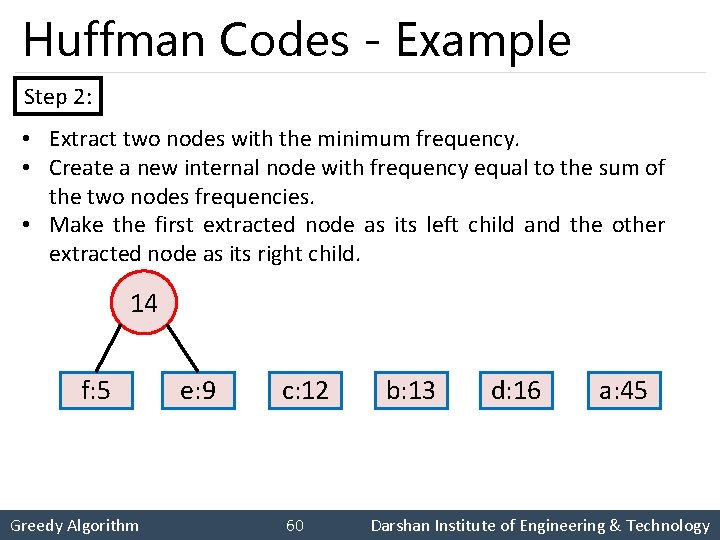
Huffman Codes - Example Step 2: • Extract two nodes with the minimum frequency. • Create a new internal node with frequency equal to the sum of the two nodes frequencies. • Make the first extracted node as its left child and the other extracted node as its right child. 14 f: 5 Greedy Algorithm e: 9 c: 12 60 b: 13 d: 16 a: 45 Darshan Institute of Engineering & Technology

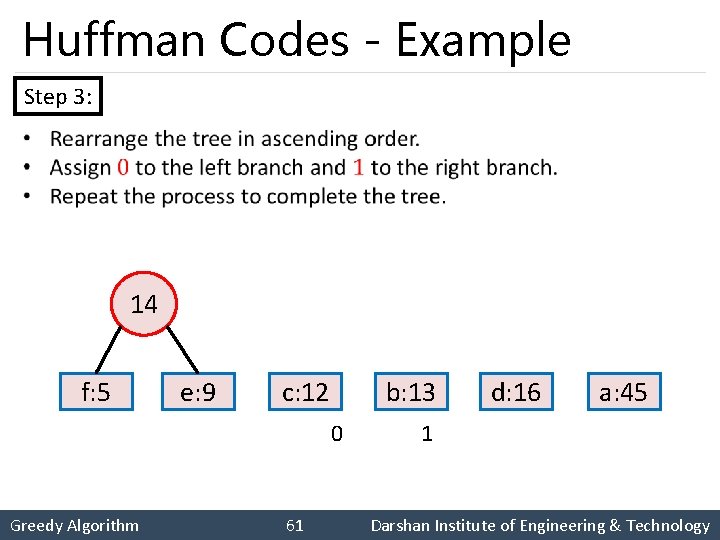
Huffman Codes - Example Step 3: 14 f: 5 e: 9 c: 12 b: 13 0 Greedy Algorithm 61 d: 16 a: 45 1 Darshan Institute of Engineering & Technology

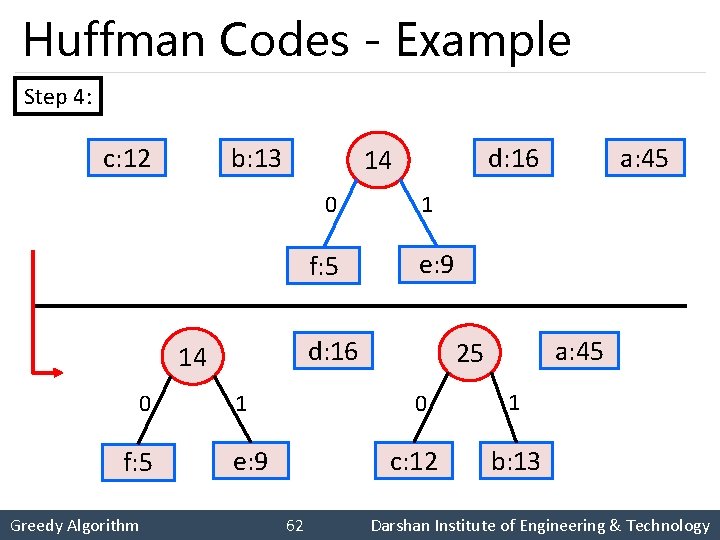
Huffman Codes - Example Step 4: c: 12 b: 13 0 f: 5 Greedy Algorithm 1 e: 9 c: 12 62 a: 45 25 0 e: 9 a: 45 1 d: 16 14 0 d: 16 14 1 b: 13 Darshan Institute of Engineering & Technology

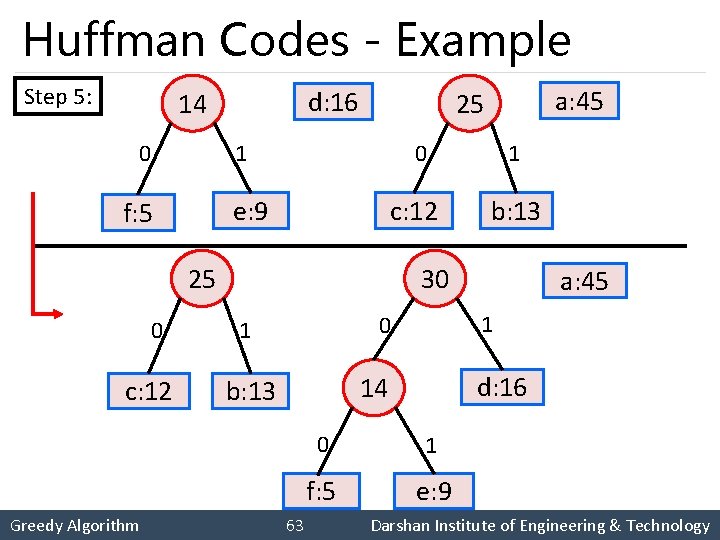
Huffman Codes - Example Step 5: d: 16 14 0 1 c: 12 25 0 c: 12 Greedy Algorithm 1 0 e: 9 f: 5 a: 45 25 b: 13 30 1 d: 16 14 b: 13 63 a: 45 0 1 f: 5 e: 9 Darshan Institute of Engineering & Technology

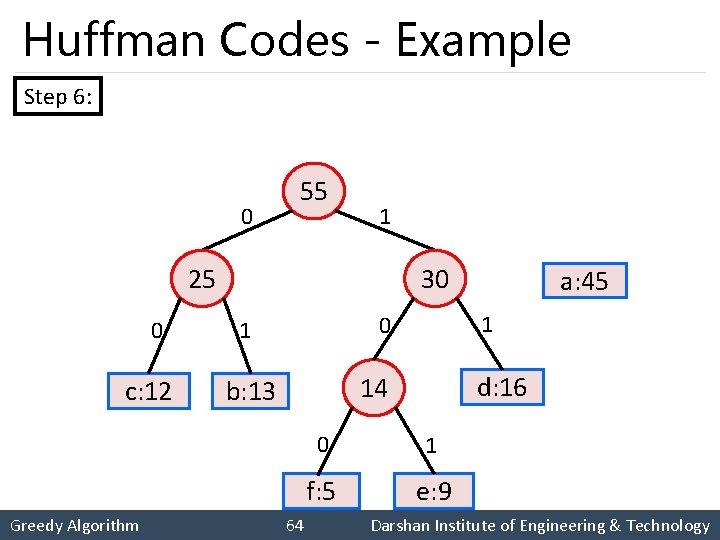
Huffman Codes - Example Step 6: 0 55 1 25 0 c: 12 Greedy Algorithm 30 1 d: 16 14 b: 13 64 a: 45 0 1 f: 5 e: 9 Darshan Institute of Engineering & Technology

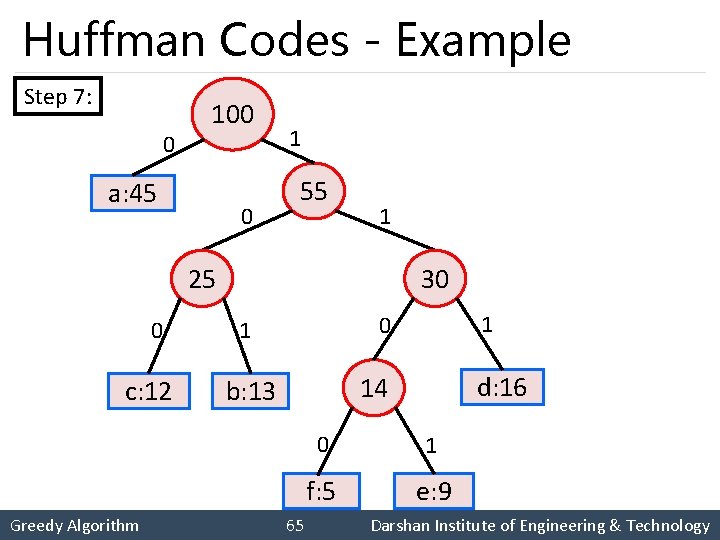
Huffman Codes - Example Step 7: 0 100 a: 45 0 1 55 1 25 0 c: 12 Greedy Algorithm 30 1 d: 16 14 b: 13 65 0 1 f: 5 e: 9 Darshan Institute of Engineering & Technology

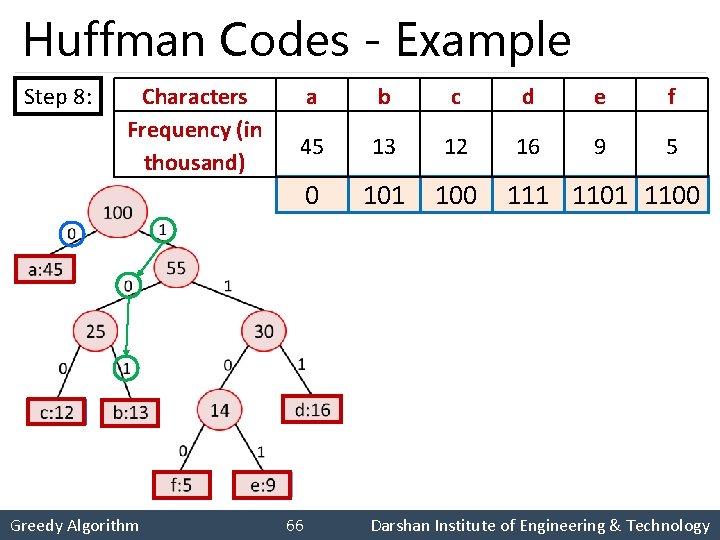
Huffman Codes - Example Step 8: Characters Frequency (in thousand) Greedy Algorithm a b c d e f 45 13 12 16 9 5 0 101 100 66 111 1100 Darshan Institute of Engineering & Technology

Huffman Codes - Algorithm: HUFFMAN (C) n = |C| Q = C for i = 1 to n-1 allocate a new node z z. left = x = EXTRACT-MIN(Q) z. right = y = EXTRACT-MIN(Q) z. freq = x. freq + y. freq INSERT(Q, z) return EXTRACT-MIN(Q) // return the root of the tree Greedy Algorithm 67 Darshan Institute of Engineering & Technology

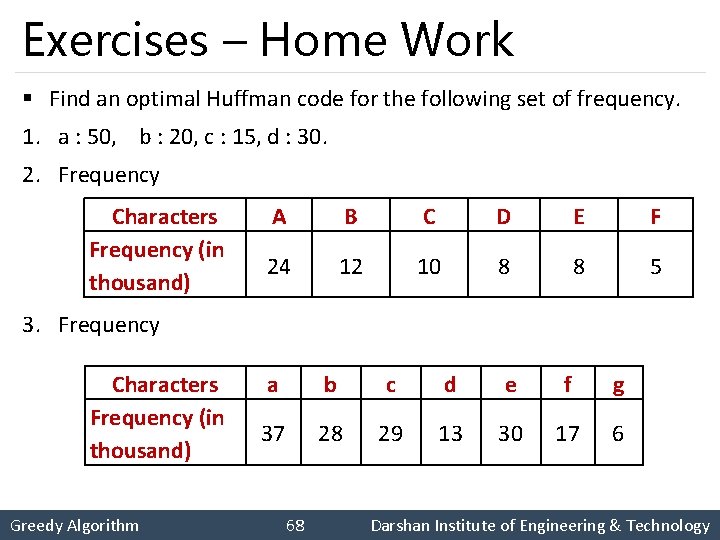
Exercises – Home Work § Find an optimal Huffman code for the following set of frequency. 1. a : 50, b : 20, c : 15, d : 30. 2. Frequency Characters Frequency (in thousand) A B C D E F 24 12 10 8 8 5 3. Frequency Characters Frequency (in thousand) Greedy Algorithm a b c d e f g 37 28 29 13 30 17 6 68 Darshan Institute of Engineering & Technology

Greedy Algorithm 69 Darshan Institute of Engineering & Technology