UNIT 5 GRAPH THEORY 5 1 GRAPHS PUZZLES

UNIT 5 GRAPH THEORY 5. 1 GRAPHS, PUZZLES, AND MAP COLORING

TOPICS Constructing mathematical models that describe the relationships that occur among a collection of objects. Theorems for practical applications

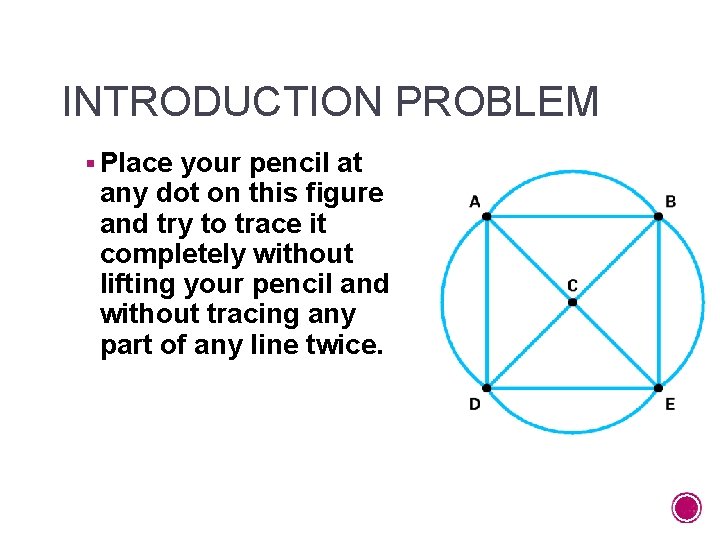
INTRODUCTION PROBLEM § Place your pencil at any dot on this figure and try to trace it completely without lifting your pencil and without tracing any part of any line twice.

INTRODUCTION PROBLEM § Were you successful? § Instead of tackling such problems using trial and error, we will learn to apply a simple test to determine whethere is a solution to tracing problems such as this.

BUT FIRST… § Terminology so we can describe this problem more precisely. § Graph: consists of a finite set of points, called vertices, and lines, called edges, that join pairs of vertices. § The figure used in our introduction problem is considered a graph. § Why? ? ?

NAMING PARTS OF GRAPHS § We use capital letters to designate vertices. § If there is only one edge joining a pair of vertices, then we label that edge by the vertices it connects. (the order is not important) § To refer to edge AB would be confusing because there are two edges joining vertices A and B. In this case we might label one edge e 1 and the other e 2.

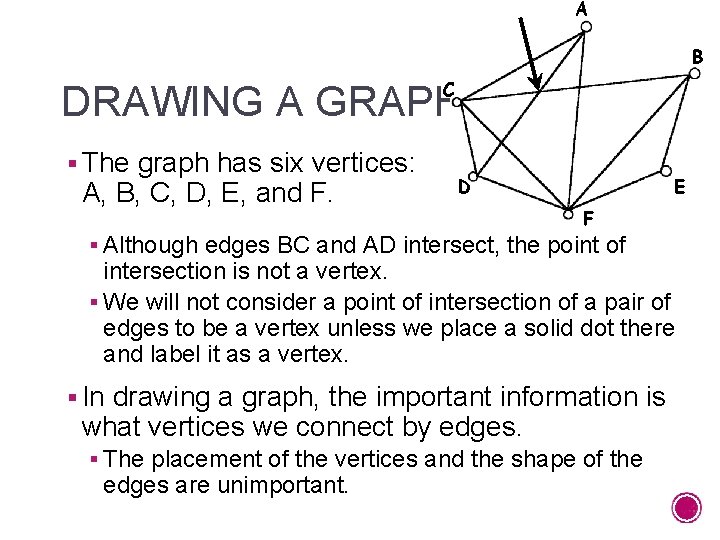
A B C DRAWING A GRAPH § The graph has six vertices: A, B, C, D, E, and F. D E F § Although edges BC and AD intersect, the point of intersection is not a vertex. § We will not consider a point of intersection of a pair of edges to be a vertex unless we place a solid dot there and label it as a vertex. § In drawing a graph, the important information is what vertices we connect by edges. § The placement of the vertices and the shape of the edges are unimportant.

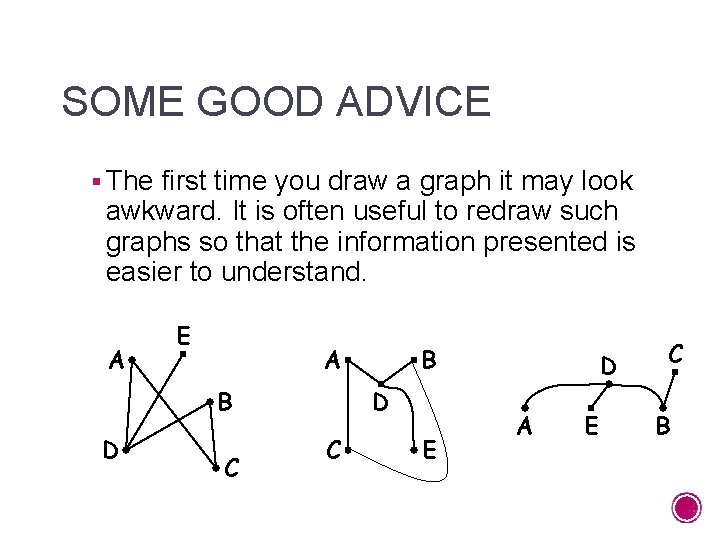
SOME GOOD ADVICE § The first time you draw a graph it may look awkward. It is often useful to redraw such graphs so that the information presented is easier to understand. A E A B D C E D A E C B

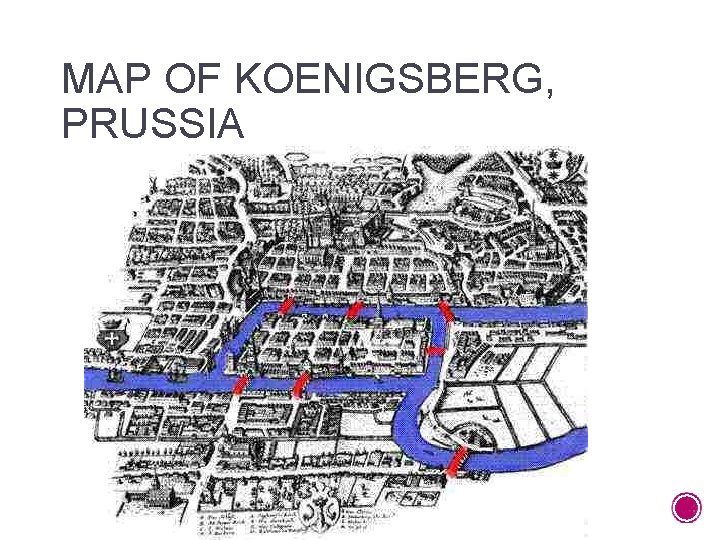
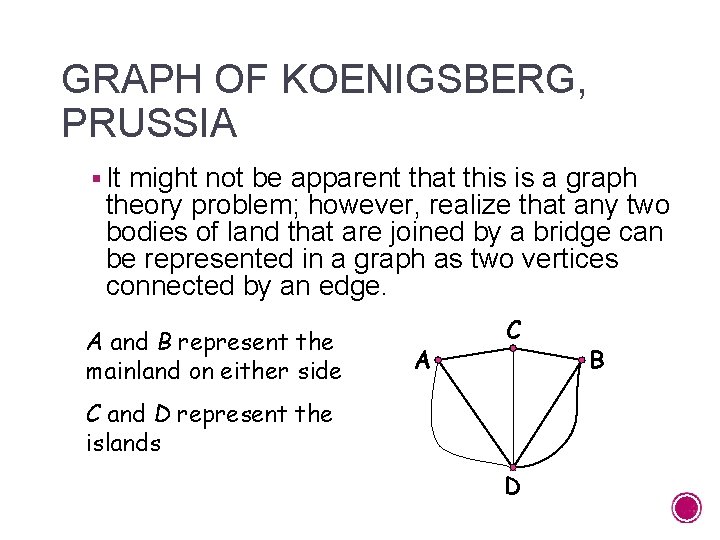
KOENIGSBERG, PRUSSIA (THE ORIGINATION OF GRAPH THEORY) § During the eighteenth century in Koenigsberg, Prussia, it was a popular pastime for the citizens of Koenigsberg to start in one section of the city and take a walk visiting all sections of the city. The Pregel River divided Koenigsberg into four distinct sections, which were connected by seven bridges. The citizens tried to do this by crossing each bridge exactly once and to return to the original starting point. This problem is called the Koenigsberg bridge problem.

MAP OF KOENIGSBERG, PRUSSIA

GRAPH OF KOENIGSBERG, PRUSSIA § It might not be apparent that this is a graph theory problem; however, realize that any two bodies of land that are joined by a bridge can be represented in a graph as two vertices connected by an edge. A and B represent the mainland on either side A C C and D represent the islands D B

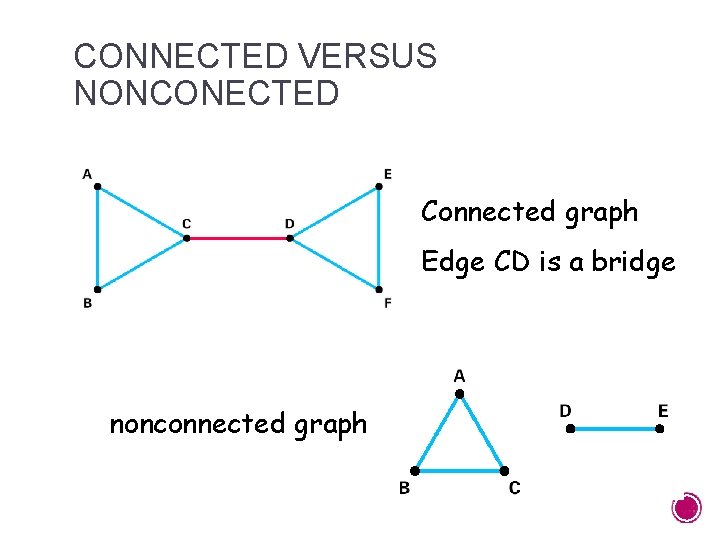
BACKGROUND § In 1735, Leonhard Euler discovered a brilliant, yet simple way to determine when a graph can be traced. § To trace a graph means to begin at some vertex and draw the entire graph without lifting your pencil and without going over any edge more than once. § A graph is connected if it is possible to travel from any vertex to any other vertex of the graph by moving along successive edges. § A bridge in a connected graph is an edge such that if it were removed the graph is no longer connected.

CONNECTED VERSUS NONCONECTED Connected graph Edge CD is a bridge nonconnected graph

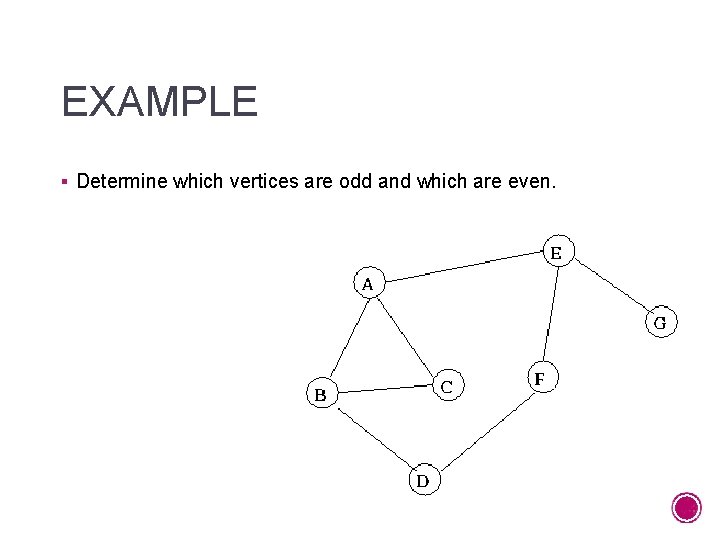
ODD AND EVEN VERTICES § A vertex of a graph is odd if it is an endpoint of an odd number of edges of the graph. § A vertex is even if it is an endpoint of an even number of edges. § For the purposes of graph theory zero edges will be considered even.

EXAMPLE § Determine which vertices are odd and which are even.

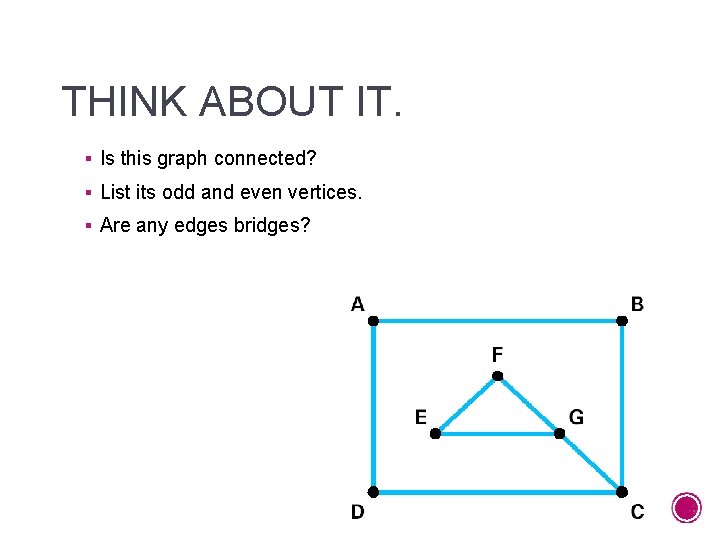
THINK ABOUT IT. § Is this graph connected? § List its odd and even vertices. § Are any edges bridges?

EXTENDING THE PROBLEM § The graph in the previous problem can be traced. § Make a hypothesis as to any rules or reasons that might allow us to determine if a graph can be traced. § Remember that once you trace an edge you can. NOT reuse it.

EULER’S THEOREM § A graph can be traced if (1) it is connected and (2) it has either no odd vertices or two odd vertices.

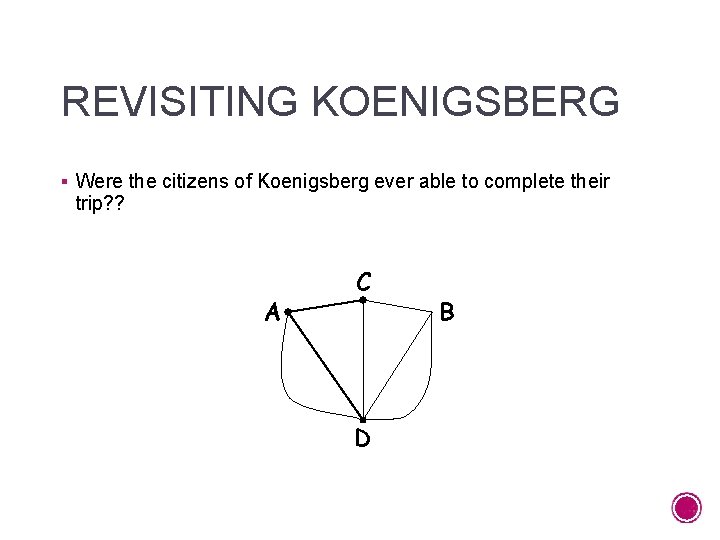
REVISITING KOENIGSBERG § Were the citizens of Koenigsberg ever able to complete their trip? ? A C D B

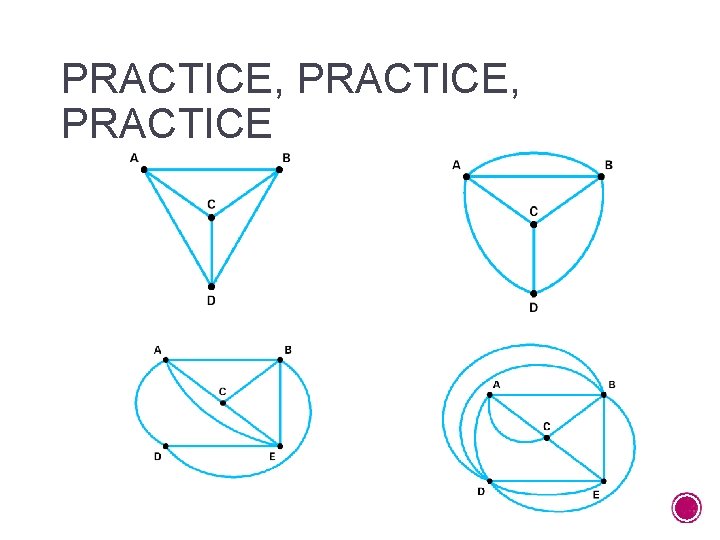
PRACTICE, PRACTICE § Using Euler’s theorem, state which of the following graphs can be traced. For a graph that can be traced, list a sequence of vertices that describes how to trace the graph. For a graph that cannot be traced, state which part of Euler’s theorem fails.

PRACTICE, PRACTICE

BUILDING A GRAPH MODEL § If we have a collection of objects with a relationship among them, then we develop a graph model as follows: 1. 2. Represent each object by a vertex. Choose names that remind you what the vertices represent. For each pair of related objects, join the two corresponding vertices with an edge.

RELATIONSHIPS AMONG OBJECTS IN SETS § For each set, state a relationship among the objects that you could model with a graph. a) a set of people b) a set of countries c) a set of animals d) a set of towns

§ Pg. 155 ( 1 – 24) Multiples of 3