UNIT 5 Fundamental principles of counting The rules



































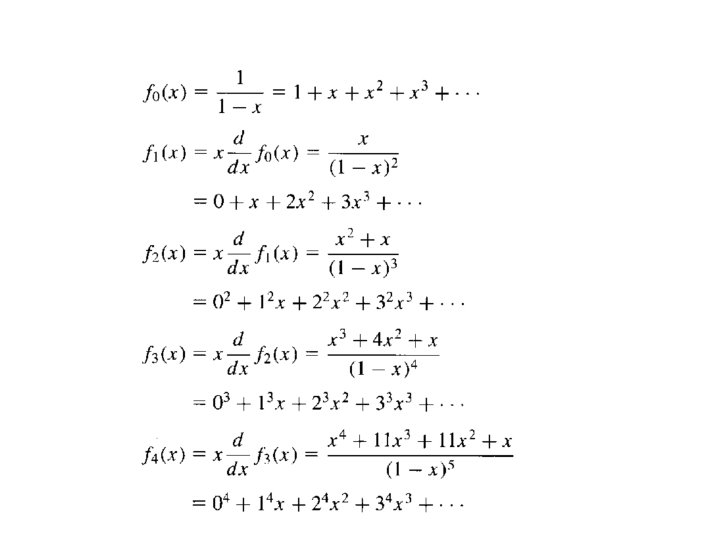



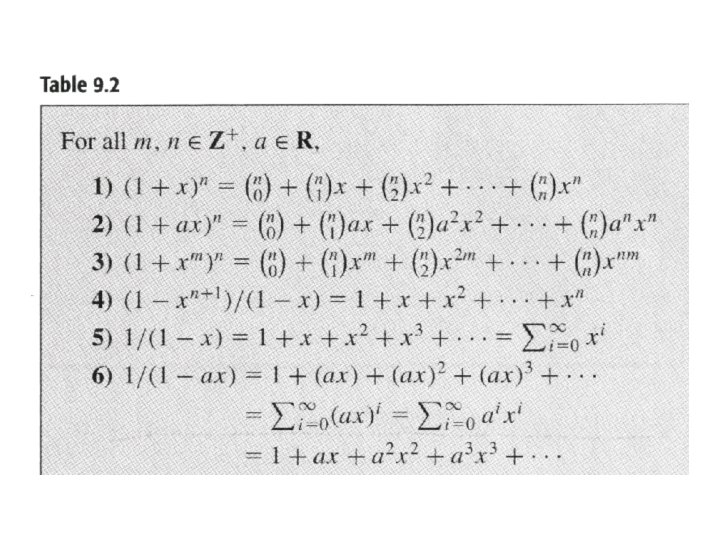
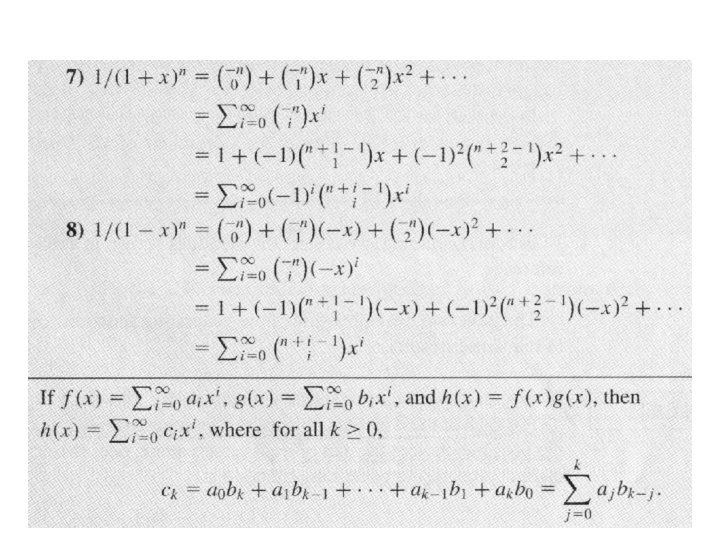





















- Slides: 64

UNIT 5 Fundamental principles of counting

The rules of sum and product • The rule of sum: If a first task can be performed in m ways, while a second task can be performed in n ways, and the tasks cannot be performed simultaneously, then performing either task can be accomplished in any one of m+n ways.

Example • • • The boss assigns 12 employees to two committees. Committee A consists of five members. Committee B consists of seven members. If the boss speak to just one member before making a decision, …? If he speak to one member of committee A on the first day, and another member of committee B on the second day, …?

The rule of product • If a procedure can be broken down into first and second stages, and if there are m possible outcomes for the first stage and if, for each of these outcomes, there are n possible outcomes for the second stage, then the total procedure can be carried out, in the designated order, in mn ways.

Example • • A license plate consists of two letters followed by four digits. If no letter or digit can be repeated? If repetitions of letters and digits are allowed, how many of the plates have only vowels (A, E, I, O, U) and even digits?

Example • • In some simple computers, one-byte address is used to identify the cells in main memory. Some uses two-byte address. Some uses four-byte address. Some even uses eight-byte address.

Permutations • Definition 1. 1. n factorial is defined by (a) 0!=1; n!=n(n-1)(n-2)…(2)(1) • Definition 1. 2. Given a collection of n distinct objects, any (linear) arrangement of these objects is called a permutation of the collection • The number of permutations of size r from a collection of n distinct objects is P(n, r)=n!/(nr)!.

Examples • Ex 1. 9. In a class of 10 students, five are to be chosen and seated in a row for a picture. How many such linear arrangements are possible? • Ex 1. 10. If five letters are to be chosen from COMPUTER, how many arrangements are there?

Example • The number of arrangements of the four letters in BALL is 12, not 24. • 2 (number of arrangements of the letters B, A, L, L) = (number of arrangements of the letters B, A, L 1, L 2)

Example • How many of arrangements are there in all nine letters in DATABASES. • 2! 3! (number of arrangements of the letters DATABASES) = (number of arrangements of the letters D, A 1, T, A 2, B, A 3, S 1, E, S 2)

Permutation with repetition • If there are n objects with n 1 indistinguishable objects of a first type, n 2 indistinguishable objects of a second type, …, and nr indistinguishable objects of an rth type, where n 1+n 2+…+nr=n, then there arrangements of the given n objects.

Example • Determine the number of staircase paths from (2, 1) to (7, 4), where each path is made up of individual steps going one unit to the right (R) or one unit upward (U). • What does RURRURRU stands for? • What does URRRUURR stands for? • There are 8!/5!3!=56 possible paths.

Example • If six people are seated about a round table, how many different circular arrangements are possible, if arrangements are considered the same when one can be obtained from the other by rotation. • 6 (number of circular arrangements) = (number of linear arrangements) • Consequently, there are 6!/6=5! arrangements.

Example • Suppose that the six people are three married couples. • We want to arrange the six people around the table so that the sexes alternate. • A female is placed first. • The next position can be placed in three ways. • The answer is 3 2 2 1 1=12.

Combinations The binomial theorem • We start with 52 cards, and how many ways are there that we can select three of these cards, with no reference to order? • (3!) (number of selections of size 3 from a deck of 52 cards) = number of permutations of size 3 for the 52 cards • C(n, r)=P(n, r)/r!=n! / r! (n-r)! • C(n, r)= C(n, n-r)

Example • To win the grand prize for Power. Ball one must match five numbers selected from 1 to 49 inclusive and then must also match the powerball, an integer from 1 to 42 inclusive. • There are totally C(49, 5) C(42, 1) = 80089128 combinations we can select the six balls.

Example • If the student must answer any seven of ten questions…. • If the student must answer three questions from the first five and four questions from the last five…. • If the student must answer seven of ten questions, where at least three are selected from the first five…. .

Example • The number of arrangements of the letters in TALLAHASSEE is 11!/ 3! 2! 2! 2! 1! 1!=831600 • How many of them have no adjacent A’s? • The answer is C(9, 3) (8!/ 2! 2! 2! 1! 1!)=84 5040=423360. (Why)

Example • alphabet ={0, 1, 2}, • A string x=x 1 x 2…xn is made up from a prescribed alphabet symbols • the weight of a string wt(x)= x 1+x 2+…+xn • Among the 310 strings of length 10, how many have even weight? • A string has even weight if and only if the number of 1’s in the string is even. • Number of 1’s can be 0, 2, 4, 6, 8, 10 • 210 + C(10, 2)28+C(10, 4)26+C(10, 6)24+C(10, 8)22+C(10, 10)

Example • Suppose that we draw five cards from a standard deck of 52 cards. a) In how many ways can we have a hand with no clubs? C(39, 5) b) In how many ways can we have a hand with at least one club? C(52, 5)-C(39, 5) c) The same question as in (b), but we compute in another way. C(13, 1) C(51, 4) d) an over-counting problem occurs in part (c), why overcounting? e) Another way to get the result of (b): C(13, 1)C(39, 4) + C(13, 2)C(39, 3) + C(13, 3)C(39, 2) + C(13, 4)C(39, 1) + C(13, 5)

The Binomial Theorem • If x and y are variables and n is a positive integers, then we have • the coefficient of x 5 y 2 in (x+y)7 is C(7, 5)=21 • the coefficient of x 5 y 2 in (2 x-3 y)7 is C(7, 5) 25 (3)2=6048

Multinomial Theorem
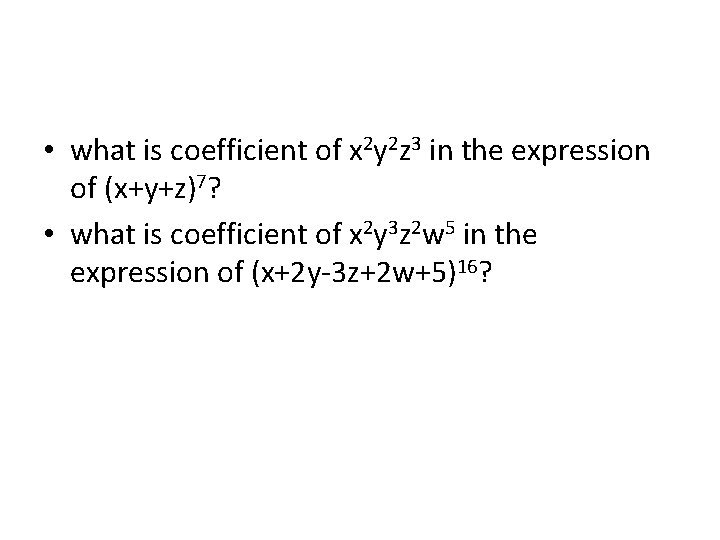
• what is coefficient of x 2 y 2 z 3 in the expression of (x+y+z)7? • what is coefficient of x 2 y 3 z 2 w 5 in the expression of (x+2 y-3 z+2 w+5)16?

1. 4. Combinations with repetition • Ex: seven students are to buy one of the following c, h, t, f.

Example • When we wish to select , with repetition, r of n distinct objects, we find that we are considering all arrangements of r x’s and n-1 |’s and that their number is • Consequently, the number of combinations of n objects taken r at a time, with repetition, is C(n+r-1, r).

Examples • A donut shop offers 20 kinds of donut. How many ways can we select a dozen donuts? C(20+12 -1, 12)=C(31, 12) • In how many ways can we distribute seven bananas and six oranges among four children so that each child receives at least one banana? C(6, 3) C(9, 6)

Example • Determine all integer solutions to the equation x 1+x 2+x 3+x 4=7 where xi 0 for i=1~4 • Each nonnegative integer solution corresponds to a selection, with repetition, of size 7 from a collection of size 4. • So, there are C(4+7 -1, 7)=120 solutions.

Example • The following are equivalent – The number of integer solutions of the equation x 1+x 2+…+xn=r, xi 0, 1 i n – The number of selections, with repetition, of size r from a collection of size n – The number of ways r identical objects can be distributed among n distinct containers

Examples • In how many ways can we distribute 10 white marbles among six distinct containers? – C(6+10 -1, 10)=3003 • How many nonnegative solutions are there to the equation x 1+x 2+x 3+x 4+x 5+x 6<10. – x 1+x 2+x 3+x 4+x 5+x 6+x 7=10, where x 7>0 and xi 0. – y 1+y 2+y 3+y 4+y 5+y 6+y 7=9, where yi 0 – C(7+9 -1, 9)=5005

Example • Determine the number of compositions of m, where m is a positive integer. • Let m be 7. • For one summand, there is only one C(6, 6). • For two summands, w 1+w 2=7 where wi>0 x 1+x 2=5 where xi 0 C(2+5 -1, 5)=C(6, 5) • For three summands, w 1+w 2+w 3=7 where wi>0 x 1+x 2+x 3=4 where xi 0 C(3+4 -1, 4)=C(6, 4) • For each positive m, there are 2 m-1 compositions.

Example • • • In how many ways can one arrange three 1’s and three 1’s so that all six partial sums are nonnegative? b 3 Given four 1’s and four 0’s, there are b 4 ways to list eight symbols so that in each list the number of 0’s never exceeds the number of 1’s. There are b 3 ways to parenthesize x 1 x 2 x 3 x 4

Introductory examples • – 12 oranges for three children, Grace, Mary, and Frank. – Grace gets at least four, and Mary and Frank gets at least two, but Frank gets no more than five. – (x 4+ x 5+ x 6+ x 7+ x 8) (x 2+ x 3+x 4+ x 5+ x 6)(x 2+ x 3+x 4+ x 5) – The coefficient of x 12 is the solution.

• Four kinds of jelly beans, Red, Green, White, Black • In how many ways can we select 24 jelly beans so that we have an even number of white beans and at least six black ones? – Red (green): 1+ x 2+…. + x 23+ x 24 – White: 1+ x 2+ x 4+…. + x 22+ x 24 – Black: x 6+ x 7+…. + x 23+ x 24 • f(x)=(1+ x 2+…. + x 23+ x 24)(1+ x 2+ x 4+…. + x 22+ x 24)(x 6+ x 7+…. + x 23+ x 24) • The coefficient of x 24 is the solution.

• How many nonnegative integer solutions are there for c 1+c 2+c 3+c 4=25? • f(x)=(1+ x 2+…. + x 24+ x 25)4 • The coefficient of x 25 is the solution.

Definition and examples: calculational techniques • (1+x)n is the generating function for the sequence C(n, 0), C(n, 1), …, C(n, n), 0, 0, 0…

Example • • • (1 -xn+1)/(1 -x) is the generating function for the sequence 1, 1, 1, …, 1, 0, 0, 0…, where the first n+1 terms are 1. 1/(1 -x) is the generating function for the sequence 1, 1, 1, …. 1/(1 -x)2 is the generating function for the sequence 1, 2, 3, 4, …. x/(1 -x)2 is the generating function for the sequence 0, 1, 2, 3, …. (x+1)/(1 -x)3 is the generating function for the sequence 12, 22, 32, 42, …. x(x+1)/(1 -x)3 is the generating function for the sequence 02, 12, 22, 32, 42, ….
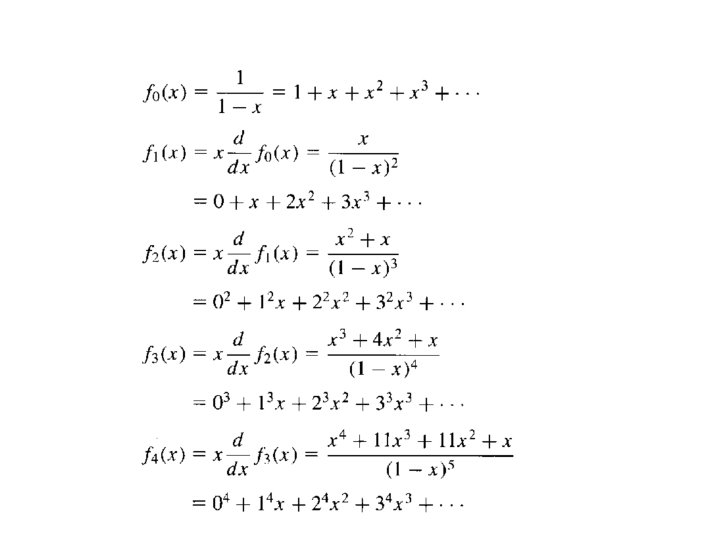

Example • • • 1/(1 -ax) is the generating function for the sequence a 0, a 1, a 2, a 3, …. Let f(x)=1/(1 -x). Then g(x)=f(x)-x 2 is the generating function for the sequence 1, 1, 0, 1, 1, …, …. Let ai=i 2+i for i 0. Then its generating function is [x(x+1)/(1 -x)3]+[x/(1 -x)2]=2 x/(1 -x)3

Define C(n, r) for n R • Since when n Z+, we have • So for n R we define • For example, if n is positive, we have

Example • Determine the coefficient of x 15 in f(x)=(x 2+x 3+x 4+…)4. • (x 2+x 3+x 4+…)=x 2(1+x+x 2+…)=x 2/(1 -x) • f(x)=(x 2/(1 -x))4=x 8/(1 -x)4 • Hence the solution is the coefficient of x 7 in (1 x)-4, which is C(-4, 7)(-1)7=C(10, 7).
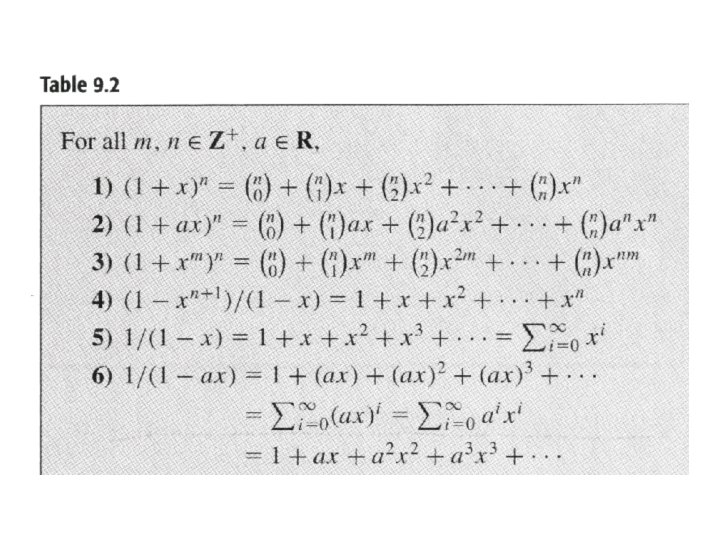
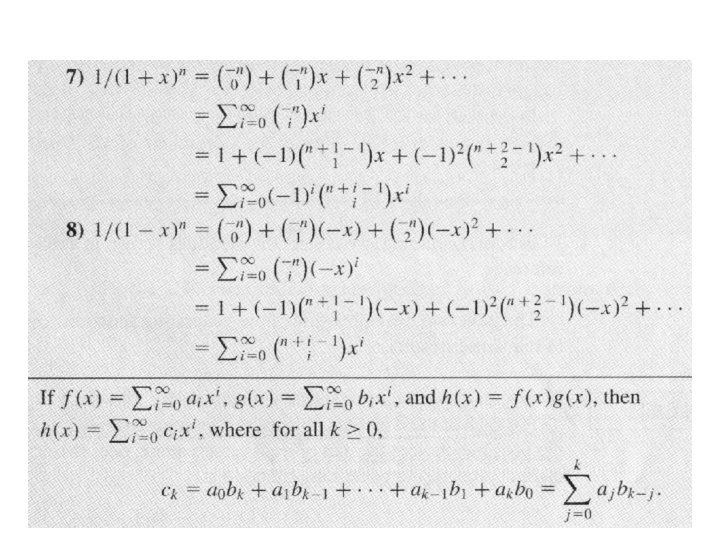

Example • In how many ways can we select, with repetition allowed, r objects from n distinct objects? • Consider f(x)=(1+x+x 2+…)n – (1/(1 -x))n=1/(1 -x)n – The coefficient of xr is C(n+r-1, r) • The answer is the coefficient of xr in f(x).

Example • x/(1 -x)= x 1+ x 2+x 3+x 4+…. • The coefficient of xj in (x 1+x 2+x 3+x 4+…. )i is the number of ways that we form the integer j by i summands. • The number of ways to form an integer n is the coefficient of xn in the following generating function.

Example • In how many ways can a police captain distribute 24 rifle shells to four police officers, so that each officer gets at least three shells but not more than eight. • f(x)= (x 3+x 4+ x 5+ x 6+x 7+x 8)4 =x 12(1+x+x 2+x 3+x 4+x 5)4 =x 12[(1 -x 6)/(1 -x)]4 • the answer is the coefficient of x 12 in (1 -x 6)4(1 -x)-4

Example • • How many four element subsets of S={1, 2, …, 15} contains no consecutive integers? {1, 3, 7, 10} 0, 2, 4, 3, 5 there exists a one-to-one correspondence between the four-element subsets to be counted and the integer solutions to c 1+c 2+c 3+c 4+c 5=14 where 0 c 1, c 5 and 2 c 2, c 3, c 4. The answer is the coefficient of x 14 in the following formula f(x)=(1+x+x 2+x 3+…)(x 2+x 3+x 4+…)3(1+x+x 2+x 3+…)=x 6(1 -x)-5

Example • • {1, 3, 7, 10} 0, 1, 3, 2, 5 there exists a one-to-one correspondence between the four-element subsets to be counted and the integer solutions to c 1+c 2+c 3+c 4+c 5=11 where 0 c 1, c 5 and 1 c 2, c 3, c 4. The answer is the coefficient of x 14 in the following formula f(x)=(1+x+x 2+x 3+…)(x+x 2+x 3+x 4+…)3(1+x+x 2+x 3+…) =x 3(1 -x)-5

Example • Brianna takes an examination until she passes it. Suppose in each test the probability of failure is 0. 8, and of success is 0. 2. • Let Y denote the number of times Brianna expects to take the exam before she passes it. • Please compute E(Y) and E(Y 2).

compute E(Y)

compute E(Y 2).

Partition of integers • p(x) is the number of partitions for x. • For n, the number of 1’s is 0 or 1 or 2 or 3…. The power series is 1+x+x 2+x 3+x 4+…. • For n, the number of 2’s can be kept tracked by the power series 1+x 2+x 4+x 6+x 8+…. • For n, the number of 3’s can be kept tracked by the power series 1+x 3+x 6+x 9+x 12+…. • f(x)=(1+x+x 2+x 3+x 4+…)(1+x 2+x 4+x 6+x 8+x 10+…) (1+x 3+x 6+x 9+…) …(1+x 10+…) =1/(1 -x) 1/(1 -x 2) 1/(1 -x 3) … 1/(1 -x 10) • At last, we have the following series for p(n) by the coefficient of xn

Example • • • Find the number of ways an advertising agent can purchase n minutes if the time slots come in blocks of 30, 60, 120 seconds. Let 30 seconds represent one time unit. a+2 b+4 c=2 n f(x)= (1+x+x 2+x 3+x 4+…) (1+x 2+x 4+x 6+x 8+…)( 1+x 4+x 8+x 12+…) =1/(1 -x) 1/(1 -x 2) 1/(1 -x 4). The coefficient of x 2 n is the answer to the problem.

Examples • Ex 9. 22. pd(n) is the number of partitions of a positive integer n into distinct summands. – Pd(x)=(1+x)(1+x 2)(1+x 3). . … • Ex 9. 23. po(n) is the number of partitions of a positive integer n into odd summands. – Po(x)= (1+x+x 2+x 3+x 4+…) (1+x 3+x 6+x 9+x 12+…)( 1+x 5+x 10+x 15+…)… – Po(x)=1/(1 -x) 1/(1 -x 3) 1/(1 -x 5) 1/(1 -x 7) . . . – Pd(x)= Po(x)

Example • poo(n) is the number of partitions of a positive integer n into odd summands and such summands must occur an odd number of times. • Poo(x)= (1+x+x 3+x 5+x 7+…) (1+x 3+x 9+x 15+…)( 1+x 5+x 15+x 25+…)…

The exponential generating function

Example • In how many ways can four of the letters in ENGINE be arranged? • f(x)=[1+x+(x 2/2!)]2[1+x]2, and the answer is the coefficient of x 4/4!.

important series

Example • We have 48 flags, 12 each of the colors red, white, blue and black. Twelve flags are placed on a vertical pole to show signal. • How many of these use an even number of blue flags and an odd number of black flags? l

Example • how many of these use at least three white flags or no white flag at all?


Example • A company hires 11 new employees, and they will be assigned to four different departments, A, B, C, D. Each department has at least one new employee. In how many ways can these assignments be done?

The summation operator • Let f(x)=a 0+a 1 x+a 2 x 2+a 3 x 3+…. Then f(x)/(1 -x) generate the sequence of a 0, a 0+a 1+a 2, a 0+a 1+a 2+a 3, … So we refer to 1/(1 -x) as the summation operator.

Example • 1/(1 -x) is the generating function for the sequence 1, 1, 1, … • [1/(1 -x)] is the generating function for the sequence 1, 2, 3, 4, 5, … • x+x 2 is the generating function for the sequence 0, 1, 1, 0, 0, 0, … • (x+x 2) /(1 -x) is the generating function for the sequence 0, 1, 2, 2, … • (x+x 2) /(1 -x)2 is the generating function for the sequence 0, 1, 3, 5, 7, 9, 11, … • (x+x 2) /(1 -x)3 is the generating function for the sequence 0, 1, 4, 9, 16, 25, 36, …
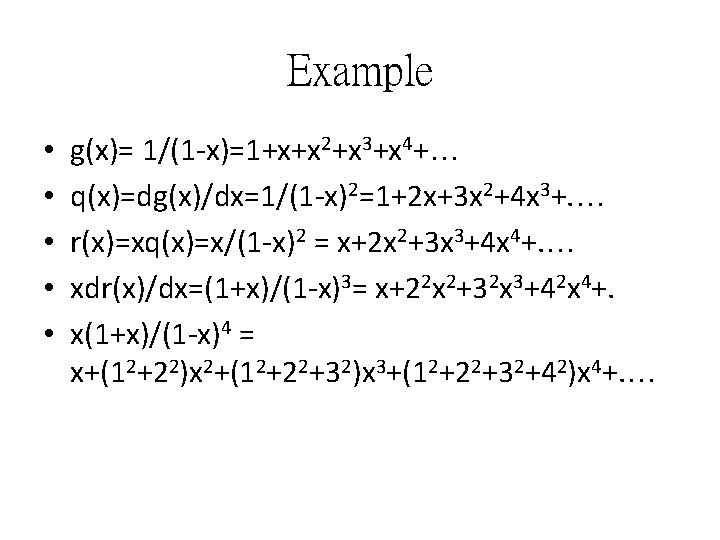
Example • • • g(x)= 1/(1 -x)=1+x+x 2+x 3+x 4+… q(x)=dg(x)/dx=1/(1 -x)2=1+2 x+3 x 2+4 x 3+. … r(x)=xq(x)=x/(1 -x)2 = x+2 x 2+3 x 3+4 x 4+. … xdr(x)/dx=(1+x)/(1 -x)3= x+22 x 2+32 x 3+42 x 4+. x(1+x)/(1 -x)4 = x+(12+22)x 2+(12+22+32)x 3+(12+22+32+42)x 4+. …