UNIT 5 4 FORMS AND PYTHAGOREAN THEOREM Final

TOPICS TO INCLUDE v 4 Forms v. Pythagorean Theorem v. Converse to the Pythagorean

4 FORMS v. The 4 Forms of a linear expression are: v 1. VERBAL

4 FORMS v. When converting from the verbal description to the algebraic equation, use

4 FORMS v. Example: Sally needs to buy a set of paint brushes and

4 FORMS v. You Try! 1. Sheila takes a ballet class. She buys a

PYTHAGOREAN THEOREM v. The Pythagorean Theorem is used to find MISSING SIDE LENGTHS in

CONVERSE TO THE PYTHAGOREAN THEOREM v. You can also use the Pythagorean Theorem to

CONVERSE TO THE PYTHAGOREAN THEOREM v. Example Side lengths: 4, 12, 10 a 2

CONVERSE TO THE PYTHAGOREAN THEOREM v. Now you try: Is the triangle a right

WORD PROBLEMS v. When solving word problems with the Pythagorean Theorem, it is very

WORD PROBLEMS v. You try! 1. The bottom of a 13 -foot straight ladder

Slides: 15

Download presentation

UNIT 5: 4 FORMS AND PYTHAGOREAN THEOREM Final Exam Review

TOPICS TO INCLUDE v 4 Forms v. Pythagorean Theorem v. Converse to the Pythagorean Theorem v. Word Problems

4 FORMS v. The 4 Forms of a linear expression are: v 1. VERBAL DESCRIPTION v 2. ALGEBRAIC EQUATION v 3. TABLE v 4. GRAPH

4 FORMS v. When converting from the verbal description to the algebraic equation, use the formula y = mx+b vm is the SLOPE vb is the Y INTERCEPT or STARTING POINT

4 FORMS v. Example: Sally needs to buy a set of paint brushes and some paint for a picture. The brushes cost $6. 98 and the paints are $1. 29 each. Slope: $1. 29 Y-Intercept: $6. 98 Equation: y = 1. 29 x + 6. 98

4 FORMS v. You Try! 1. Sheila takes a ballet class. She buys a tutu for $34 and pays $15 per hour for the class. 2. Franklin buys a turtle for $14 at Pet’s Mart. He also has to buy food, which is $2. 99 per pound.

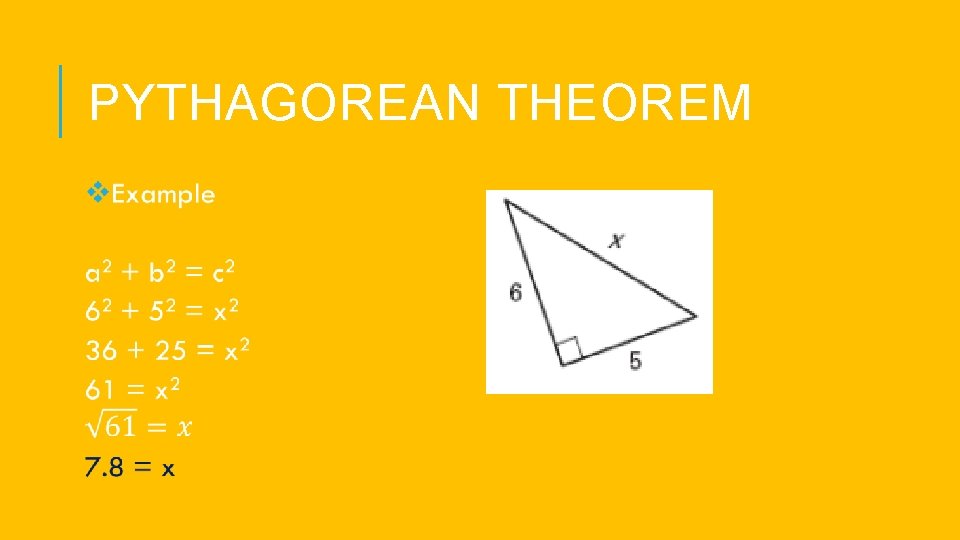
PYTHAGOREAN THEOREM v. The Pythagorean Theorem is used to find MISSING SIDE LENGTHS in RIGHT triangles. v. The theorem: a 2 + b 2 = c 2 va and b are the LEGS vc must be the HYPOTENUSE

PYTHAGOREAN THEOREM

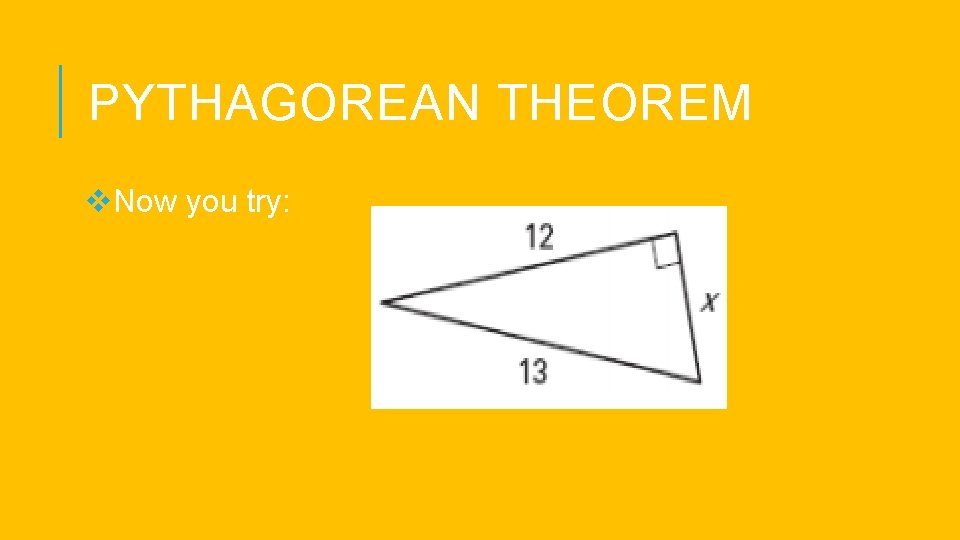
PYTHAGOREAN THEOREM v. Now you try:

CONVERSE TO THE PYTHAGOREAN THEOREM v. You can also use the Pythagorean Theorem to determine if a triangle is a RIGHT triangle v. If you perform the Pythagorean Theorem and the equation is EQUAL, then the triangle IS a right triangle v. If you perform the Pythagorean Theorem and the equation is NOT EQUAL, then the triangle is NOT a right triangle

CONVERSE TO THE PYTHAGOREAN THEOREM v. Example Side lengths: 4, 12, 10 a 2 + b 2 = c 2 42 + 102 = 122 16 + 100 = 144 116 = 144 Since 144 is not equal to 116, the triangle is NOT RIGHT

CONVERSE TO THE PYTHAGOREAN THEOREM v. Now you try: Is the triangle a right triangle? 1. Side lengths: 9, 40, 41 2. Side lengths: 8, 7, 5

WORD PROBLEMS v. When solving word problems with the Pythagorean Theorem, it is very important that you put the right NUMBERS on the right SIDE of the triangle. v. Example: Jerry climbed up to the top of a slide and then slid down. He had so much fun that he wants to do it again. If he climbed up 6 ft and then slid down the 13 ft long slide, how far does he have to walk to get back to the ladder 6 + b = 13 where he can climb back up? 13 ft 2 6 ft 2 2 36 + b 2 = 169 b 2 = 133 b = 11. 5 ft

WORD PROBLEMS v. You try! 1. The bottom of a 13 -foot straight ladder is set into the ground 5 feet away from a wall. When the top of the ladder is leaned against the wall, what is the distance above the ground it will reach? 2. David leaves the house to go to school. He walks 200 m west and 125 m north. Calculate how far he is from the starting point.

ALL DONE