UNIT 4 WORK ENERGY II Conservation of Energy









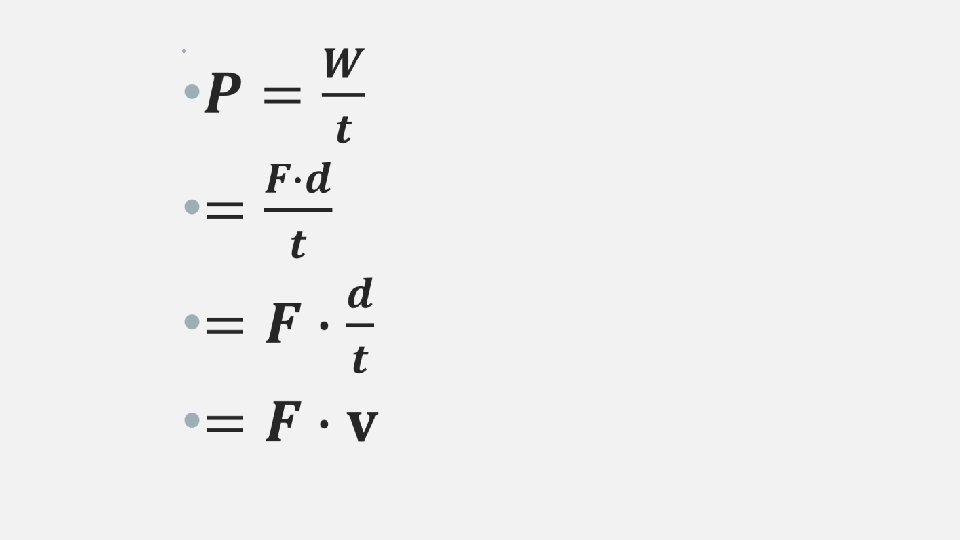

- Slides: 12

UNIT 4: WORK & ENERGY II Conservation of Energy & Power

KINETIC ENERGY • Kinetic Energy is the energy of motion KE = ½mv 2 m = mass of object v = speed of object • KE is always zero or positive, never negative • Net work done on an object results in a change in kinetic energy: Wnet = KE

POTENTIAL ENERGY • Potential energy is stored energy • An object has potential energy because of its relative position to other objects • Only a change in potential energy matters • Gravitational potential energy is stored energy because of an objects position relative to earth PEg = mgh h = height above zero level • The zero level is arbitrary

POTENTIAL ENERGY (CONT. ) • Elastic potential energy is energy stored in a compressed or stretched object • Classic example is a spring: PEs = ½ kx 2 k = the spring constant x = distance object is stretch or compressed • Spring constant k (units = N/m) is a measure of how stiff the spring is

EXAMPLE OF POTENTIAL ENERGY • How high can a dart gun (k = 100 N/m) shoot a 3. 1 g dart, given that the spring is compressed 4. 0 cm?

ANSWER: At the highest point, the energy of the compressed spring becomes PEg: ½ kx 2 = mgh h = kx 2/(2 mg) = (100 N/m)(. 040 m)2/ m/s 2)] [2(. 0031 kg)(9. 8 = 2. 6 m

CONSERVATION OF MECHANICAL ENERGY • Kinetic and potential energy are the two types of mechanical energy • The total mechanical energy of an object or group of objects is ME = KE + PEg + PEs + … • If there is no friction, then ME is conserved: MEi = MEf KEi + PEi = KEf + PEf

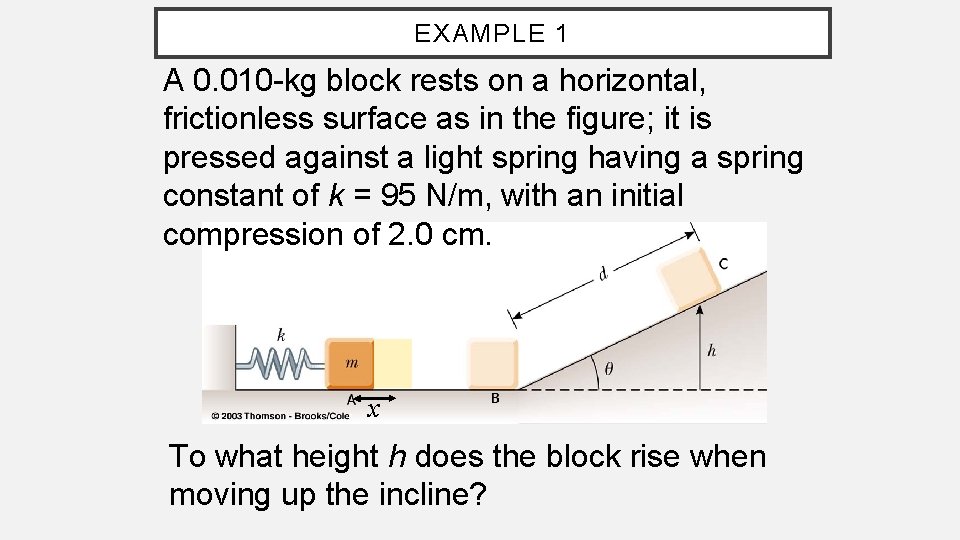
EXAMPLE 1 A 0. 010 -kg block rests on a horizontal, frictionless surface as in the figure; it is pressed against a light spring having a spring constant of k = 95 N/m, with an initial compression of 2. 0 cm. x To what height h does the block rise when moving up the incline?

POWER • Power is the rate of energy transfer • SI units are Watts (W) = 1 J/s • 1 horse power (hp) = 746 W

• A new conveyor system at the local packaging plan will utilize a motorpowered mechanical arm to exert an average force of 890 N to push large crates a distance of 12 meters in 22 seconds. Determine the power output required of such a motor.
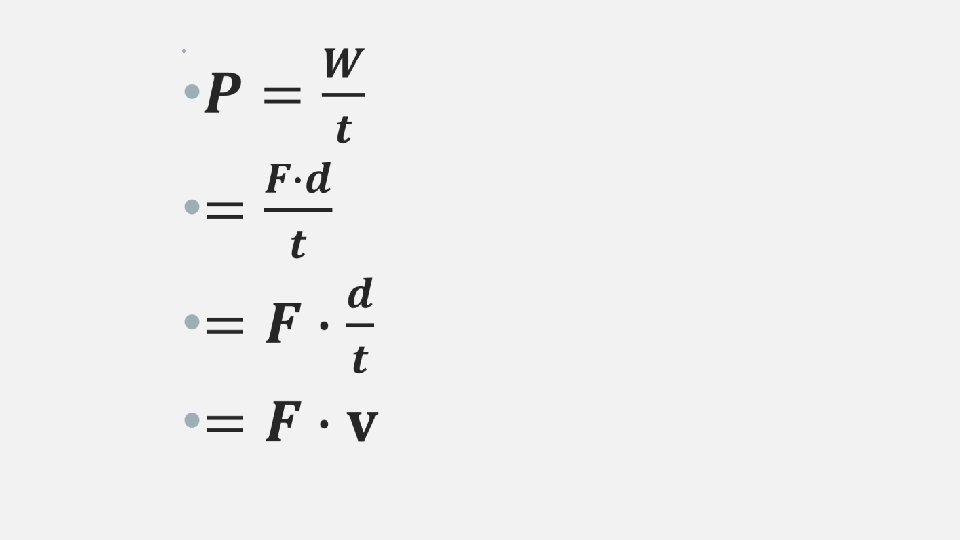

• The ski slopes at Bluebird Mountain make use of tow ropes to transport snowboarders and skiers to the summit of the hill. One of the tow ropes is powered by a 22 -k. W motor which pulls skiers along an icy incline of 14° at a constant speed. Suppose that 18 skiers with an average mass of 48 kg hold onto the rope and suppose that the motor operates at full power. • a. Determine the cumulative weight of all these skiers. b. Determine the force required to pull this amount of weight up a 14° incline at a constant speed. c. Determine the speed at which the skiers will ascend the hill.