Unit 4 Waves Part E Reflection Refraction Table

Unit 4: Waves Part E: Reflection & Refraction

Table of Contents The Law of Reflection Specular vs. Diffuse Reflection Refraction Introduced Snell’s Law Total Internal Reflection Refraction & Dispersion of Colors

Reflection is the bouncing of a wave off of a boundary between one medium and another. We’ve already encountered one kind of reflection in our study of waves: echoes – reflections of sound. We’ll now consider reflection as it pertains to light.

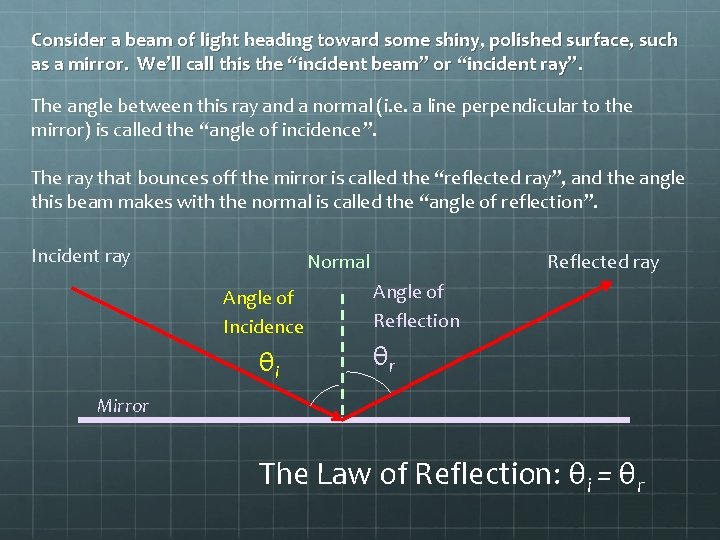
Consider a beam of light heading toward some shiny, polished surface, such as a mirror. We’ll call this the “incident beam” or “incident ray”. The angle between this ray and a normal (i. e. a line perpendicular to the mirror) is called the “angle of incidence”. The ray that bounces off the mirror is called the “reflected ray”, and the angle this beam makes with the normal is called the “angle of reflection”. Incident ray Normal Angle of Incidence θi Reflected ray Angle of Reflection θr Mirror The Law of Reflection: θi = θr

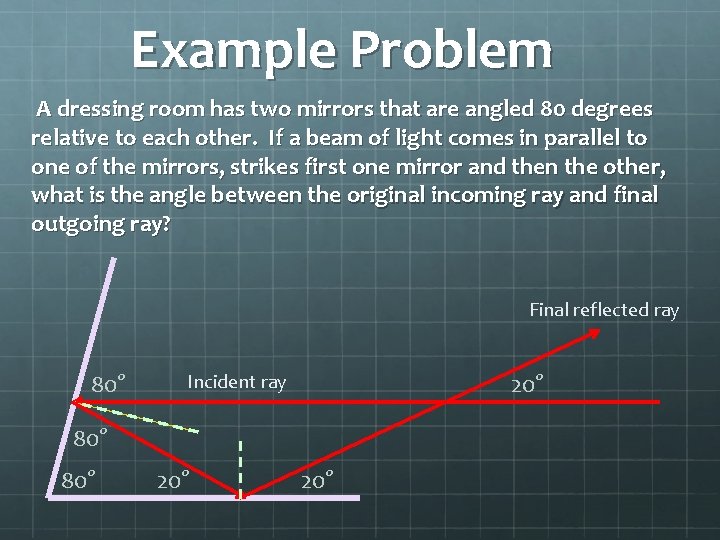
Example Problem A dressing room has two mirrors that are angled 80 degrees relative to each other. If a beam of light comes in parallel to one of the mirrors, strikes first one mirror and then the other, what is the angle between the original incoming ray and final outgoing ray? Final reflected ray 80° 20° Incident ray 80° 20°

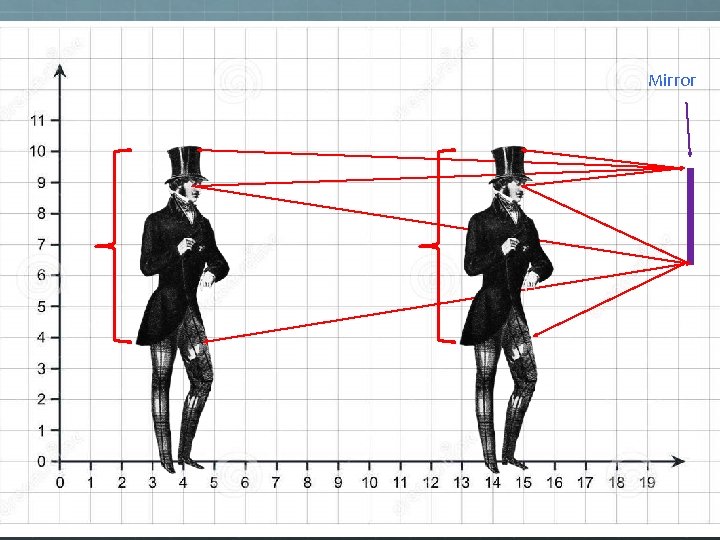
Question: If you are looking at yourself in a mirror, and then back away from the mirror, what should happen? A) You should see more of your reflection. B) You should see less of your reflection. C) You should see the same amount of your reflection. D) You should see yourself winning the Quidditch Cup. E) You’re a vampire, and this is a trick question.

Mirror

Mirror

Mirror

Question: If you are looking at yourself in a mirror, and then back away from the mirror, what should happen? A) You should see more of reflection. B) You should see less of reflection. C) You should see the same amount of your reflection. D) You should see yourself winning the Quidditch Cup. E) You’re a vampire, and this is a trick question.

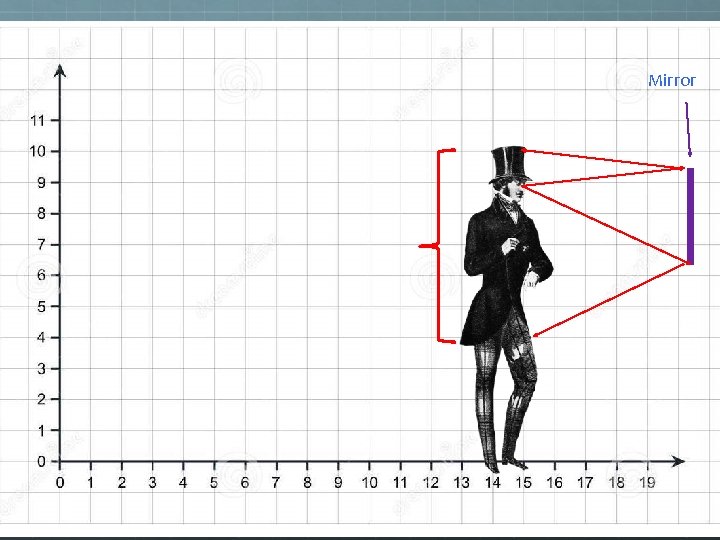
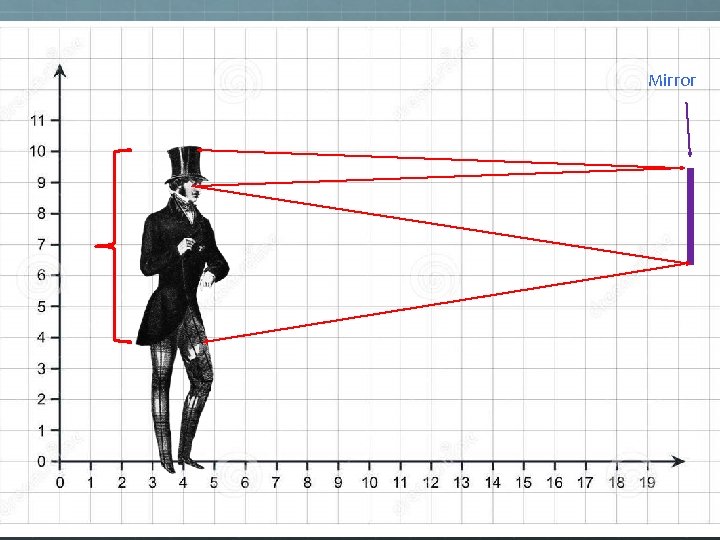
So how large a mirror would you need to see your whole reflection? A) More than your exact height B) Your exact height C) Half your height D) Less than half your height E) It depends on how far you are from the mirror.

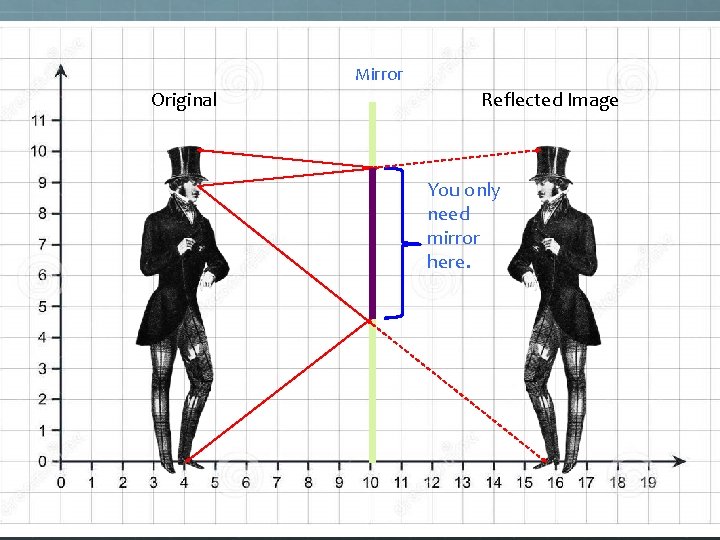
Mirror Original Reflected Image You only need mirror here.

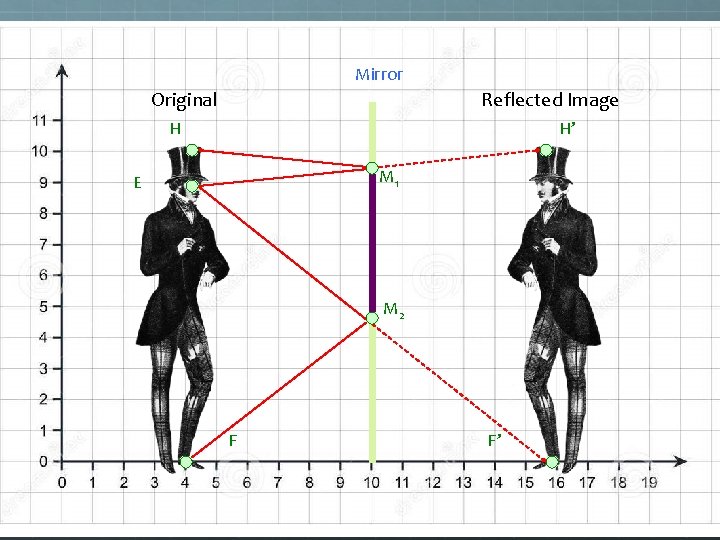
Mirror Original Reflected Image H H’ M 1 E M 2 F F’

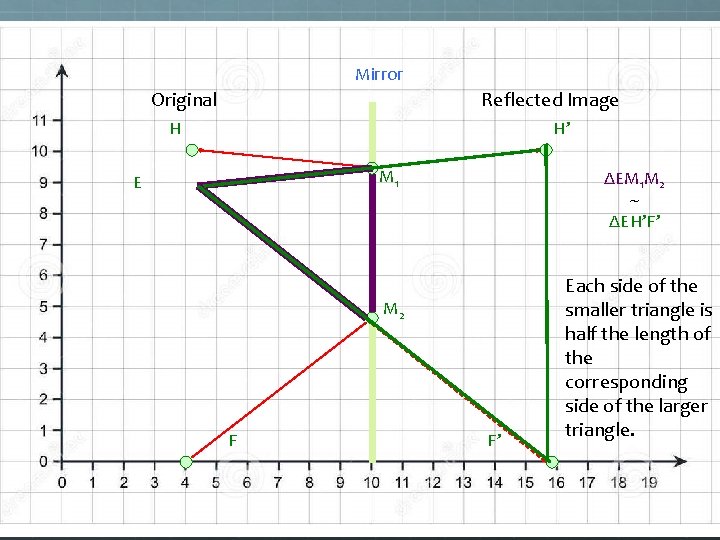
Mirror Original Reflected Image H H’ M 1 E ΔEM 1 M 2 ~ ΔEH’F’ M 2 F F’ Each side of the smaller triangle is half the length of the corresponding side of the larger triangle.

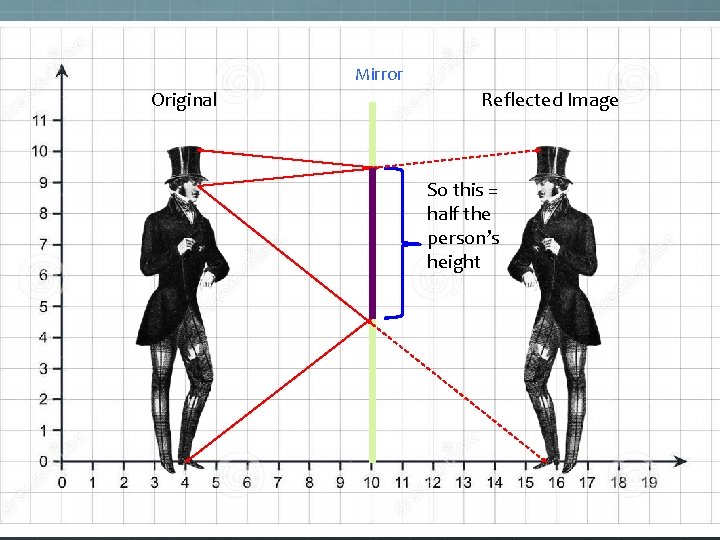
Mirror Original Reflected Image So this = half the person’s height

So how large a mirror would you need to see your whole reflection? A) More than your exact height B) Your exact height C) Half your height D) Less than half your height E) It depends on how far you are from the mirror.

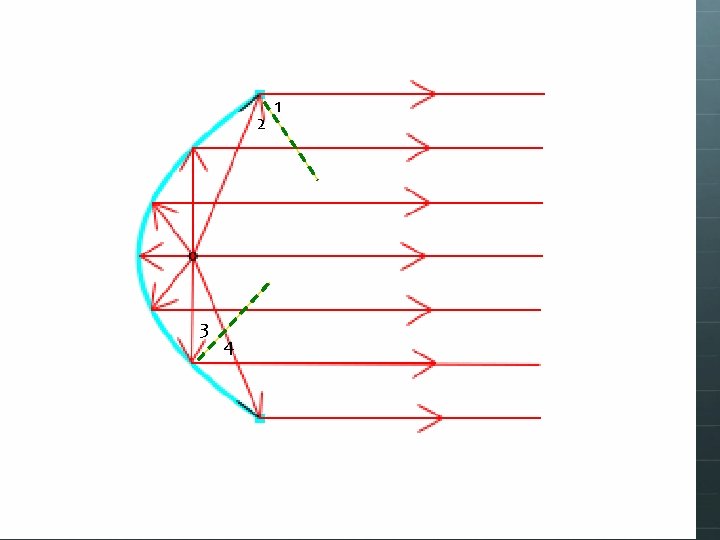
Does the Law of Reflection hold if the mirror is curved? Yes! This is how the parabolic mirrors in flashlights and headlights take light from a bulb which is heading in all directions, and bends each beam so they are parallel.

2 3 4 1

Specular (aka “Regular”) Reflection When we think of reflection, we tend to think of mirrors. In other words, we think about “specular reflection” This is also known as “regular reflection”. This occurs when parallel beams reflect off of a smooth surface as parallel beams.

Diffuse (aka “Irregular”) Reflection Most surfaces are not mirror smooth. Thus most reflection is not specular. When light is incident upon a rough* surface, it scatters in multiple directions. This is called “diffuse” or “irregular reflection” and this is how we can see most objects around us. n Note: The Law of Reflection is still obeyed at the microscopic level – each irregularity in a rough surface can be thought of as a very tiny mirror.

Another example of “irregular reflection” Involves dwelling on the fact that one’s diet doesn’t include enough fiber. Not really relevant to our discussion of light.

Refraction We have finished our discussion of reflection and are now ready to begin refraction! First, write the number 2/3 somewhere handy (on your guided notes page or on a piece of scratch paper) Now write the number 2/3 again. Congratulations! You have mastered one form of refraction!

Refraction of Light n Note: 3. 00 x 108 m/s is the speed of light in a vacuum. n In transparent materials, such as water and glass, light travels slower. n When light enters a new medium at an angle, it pivots as it slows down. n This phenomenon is called refraction.

Why does Refraction Occur? n Consider two wheels on an axle rolling from a smooth surface, such as concrete, onto a rougher surface, such as grass. n When both wheels are on the grass, both wheels are moving the same speed. n When one wheel is on the grass and one on the concrete, it starts to pivot since one wheel is moving slower than the other. n When both wheels are on the grass, the path straightens back out, and both wheels are now rolling at the same (slower) speed.

n Similarly, wave fronts of light bend as light passes into a medium where the speed of light is slower. n Note: no refraction occurs if a beam of light strikes a surface directly, since the entire wave front slows down all at once.

Index of Refraction Every transparent material may be described by an “index of refraction”: n = c/ v Where: c = speed of light in a vacuum (3. 00 x 108 m/s) v = speed of light in that material Some examples: nair = 1. 0003 nwater = 1. 33 nglass = 1. 52 ndiamond = 2. 41

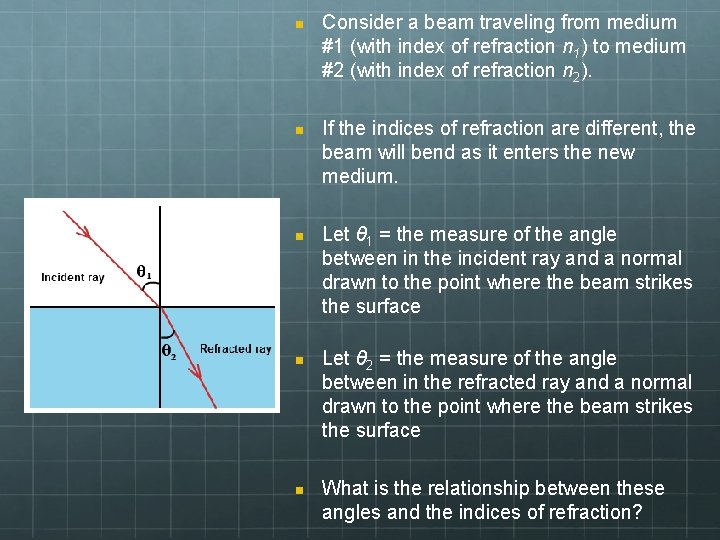
n n n Consider a beam traveling from medium #1 (with index of refraction n 1) to medium #2 (with index of refraction n 2). If the indices of refraction are different, the beam will bend as it enters the new medium. Let θ 1 = the measure of the angle between in the incident ray and a normal drawn to the point where the beam strikes the surface Let θ 2 = the measure of the angle between in the refracted ray and a normal drawn to the point where the beam strikes the surface What is the relationship between these angles and the indices of refraction?

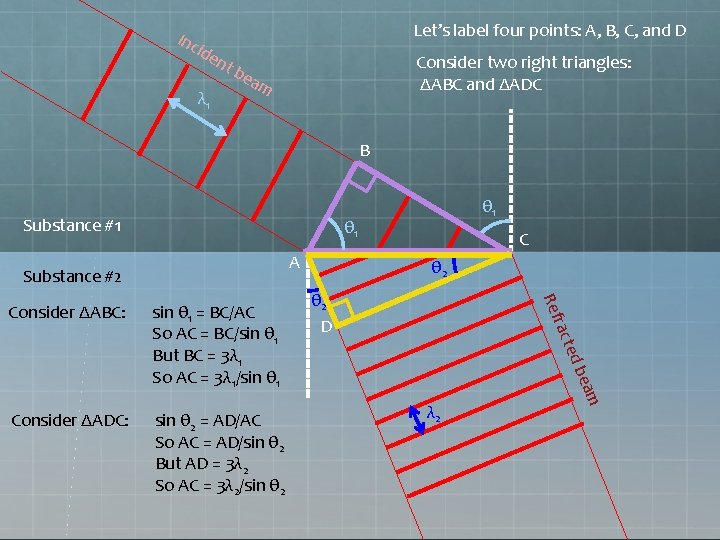
Let’s label four points: A, B, C, and D Inc ide nt λ 1 Consider two right triangles: ΔABC and ΔADC be a m B Substance #1 θ 1 A Substance #2 λ 2 m bea sin θ 2 = AD/AC So AC = AD/sin θ 2 But AD = 3λ 2 So AC = 3λ 2/sin θ 2 ted Consider ΔADC: θ 2 D rac sin θ 1 = BC/AC So AC = BC/sin θ 1 But BC = 3λ 1 So AC = 3λ 1/sin θ 1 θ 2 Ref Consider ΔABC: C

So now we can equate our two expressions for AC: 3λ 1 sin θ 1 = 3λ 2 sin θ 2 We cancel the 3’s and rewrite this as: sin θ 1 = sin θ 2 λ 1 λ 2 Note: • Index of refraction is inversely proportional to velocity: n ~ 1/v • Velocity is directly proportional to wavelength: v ~ λ • So wavelength is inversely proportional to index of refraction: λ ~ 1/n

Since λ ~ 1/n now we can write: sin θ 1 = sin θ 2 n 1 Cross-multiply, and we now have what is known as “Snell’s Law”: n 1 sin θ 1 = n 2 sin θ 2 ( An alternative form of Snell’s law: sin θ 1 = sin θ 2 v 1 v 2 )

Snell’s Law n The mathematical relationship which describes how much a beam of light bends when entering a new medium is called Snell’s Law: n 1 sin θ 1 = n 2 sin θ 2 n Where: u n 1 = the index of refraction in the initial medium u θ 1 = the measure of the angle between in the incident ray and a normal drawn to the point where the beam strikes the surface u n 2 = the index of refraction in the new medium u θ 2 = the measure of the angle between in the refracted ray and a normal drawn to the point where the beam strikes the surface

Example Problem If a beam of light strikes the surface of water at a 43. 2° angle, at what angle will the beam of light travel through the water? (Note: In order to do problems involving refraction and Snell’s Law, we need to make a couple of default assumptions. Unless we’re given information to the contrary, assume. . . 1). . . the original medium in each problem is air (and thus n = 1. 0003) 2). . . all angle measurements are given relative to the normal)

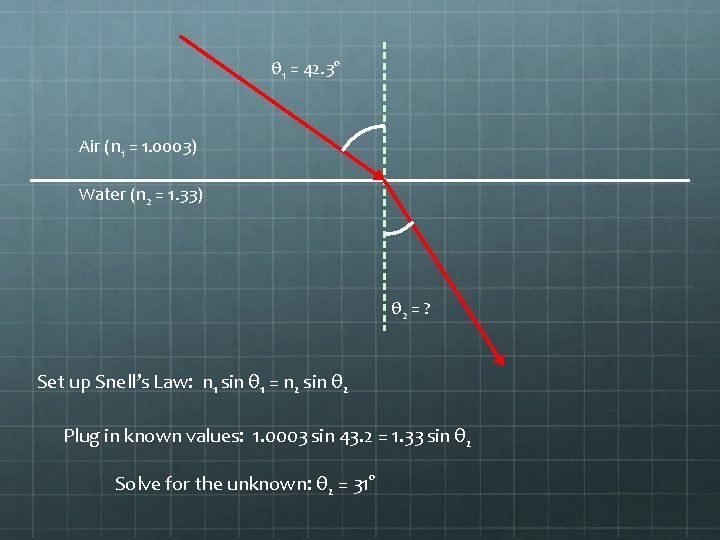
θ 1 = 42. 3° Air (n 1 = 1. 0003) Water (n 2 = 1. 33) θ 2 = ? Set up Snell’s Law: n 1 sin θ 1 = n 2 sin θ 2 Plug in known values: 1. 0003 sin 43. 2 = 1. 33 sin θ 2 Solve for the unknown: θ 2 = 31°

Critical Angle for Total Internal Reflection n n If a ray begins in the more optically dense medium, i. e. the one with the higher index of refraction, the ray will bend away from the normal, speeding up as it enters the new medium. In this case θ 2 > θ 1. If θ 1 = the so-called “critical angle, ” then θ 2 will = 90°. In this case, the refracted ray will simply skim the surface of the material. If θ 1 > θcritical, then the beam cannot refract out, and simply reflects back into the original medium, as if the boundary between the media were a mirror. This phenomenon is called “total internal reflection. ”

Another Example Problem What is the critical angle for total internal reflection for light emerging from glass into air?

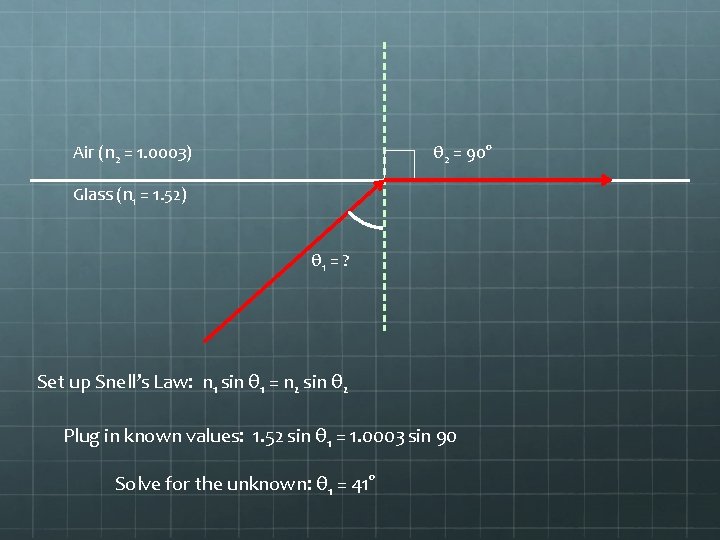
Air (n 2 = 1. 0003) θ 2 = 90° Glass (n 1 = 1. 52) θ 1 = ? Set up Snell’s Law: n 1 sin θ 1 = n 2 sin θ 2 Plug in known values: 1. 52 sin θ 1 = 1. 0003 sin 90 Solve for the unknown: θ 1 = 41°

Refraction & Dispersion White light = all colors The higher the frequency of light, the more it slows down when entering a new medium. Thus different colors bend different amounts when refracting. This is called dispersion.

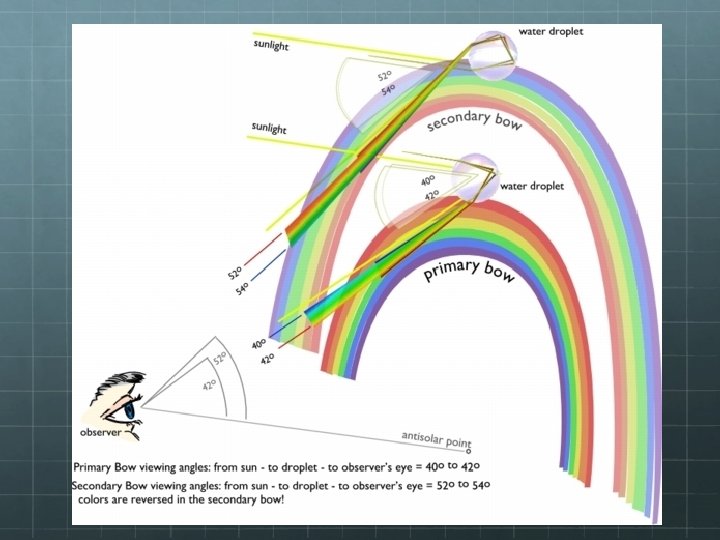
This is why rainbows can form when light encounters prisms or raindrops.

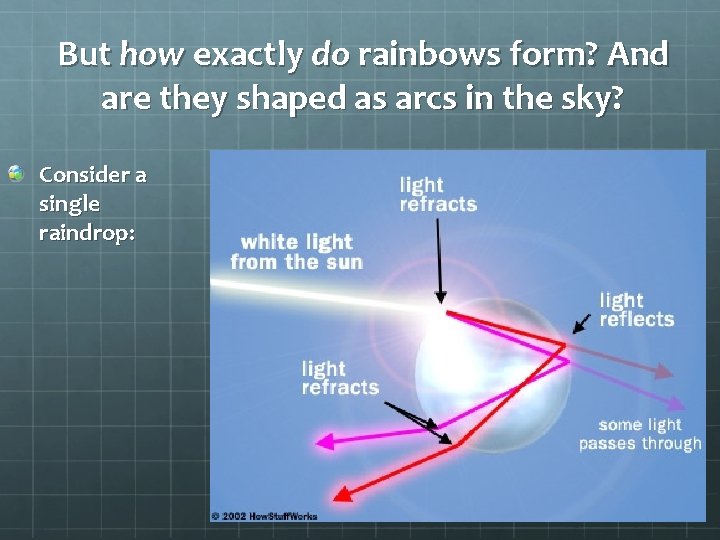
But how exactly do rainbows form? And are they shaped as arcs in the sky? Consider a single raindrop:

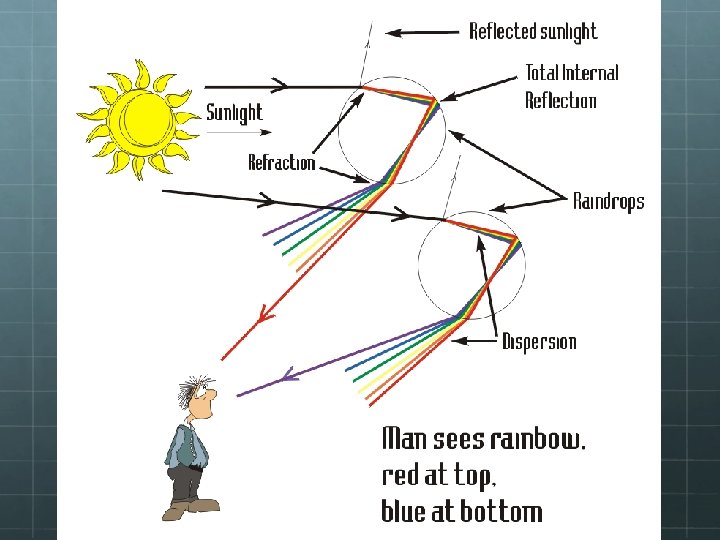
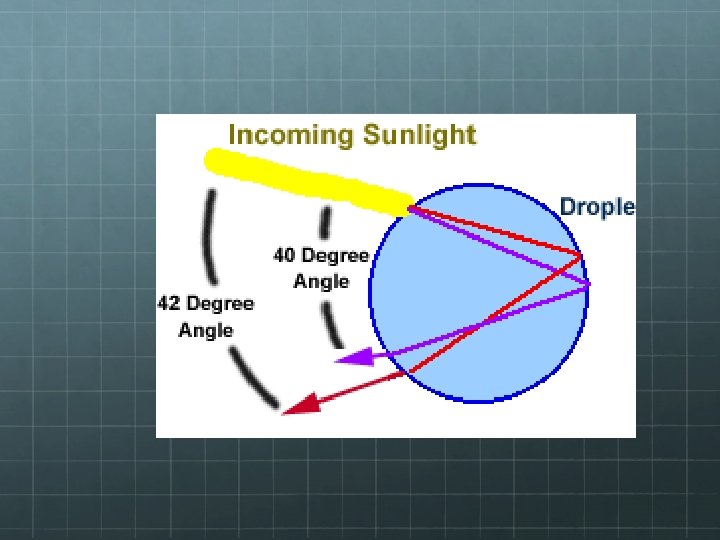
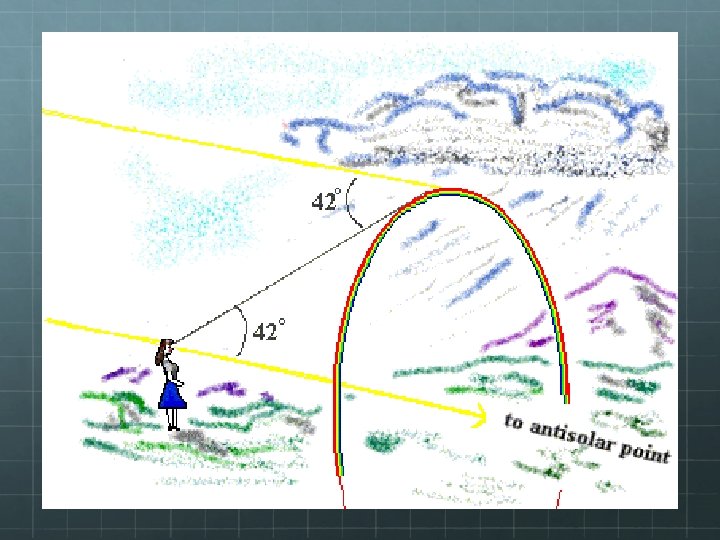
What about double rainbows?

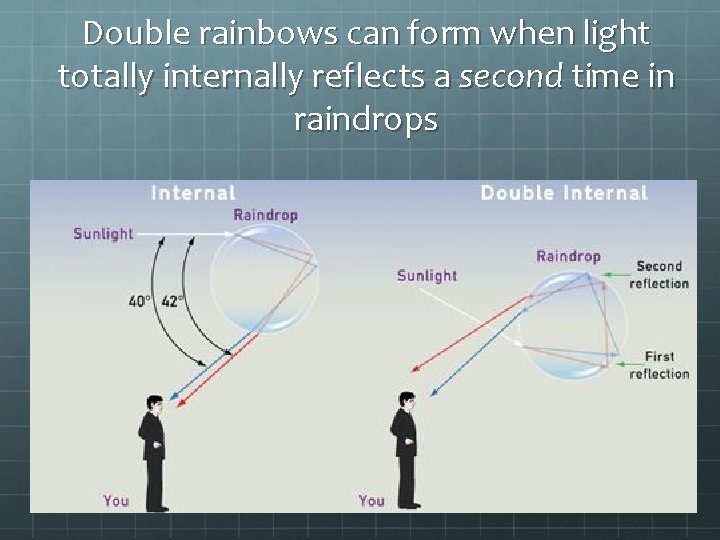
Double rainbows can form when light totally internally reflects a second time in raindrops