Unit 4 Vectors 2 DParabolic Motion Physics Comp

Unit 4 Vectors & 2 -D/Parabolic Motion

Physics Comp Book p. 21 UNIT 4: Vectors & 2 -D/Projectile Motion Student will: n SP 1 b. compare and contrast scalar and vector quantities; n SP 1 c. compare algebraically the relationships between time, distance, velocity and acceleration; n SP 1 f. measure and calculate two dimensional motion (projectile…) by using component vectors Page 22 23 24 25 26 27 Contents parabolic motion, projectile range, time of flight trajectory, Pythagorean theorem vectors, triangles and trigonometry diagrams Ex: solving a 2 -D problem Lab SUMUP:

One dimension vs. two dimensions n So far, we have only talked about the motion of objects that travel in either the x or the y direction… only one dimension at a time. n What do these vectors look like: a ball thrown directly up? n a car traveling on a highway? n

One dimension vs. two dimensions n …but sometimes, things don’t travel in a direction that’s completely vertical or completely horizontal…for example, what would these vectors look like: A football field goal kick? n A basketball free throw shot? n How about a ballerina leaping across the stage? n A ball rolled off the edge of a table? n n Notice how the initial velocity is a certain direction and the motion path doesn’t continue in that same direction…look at the next examples, too…

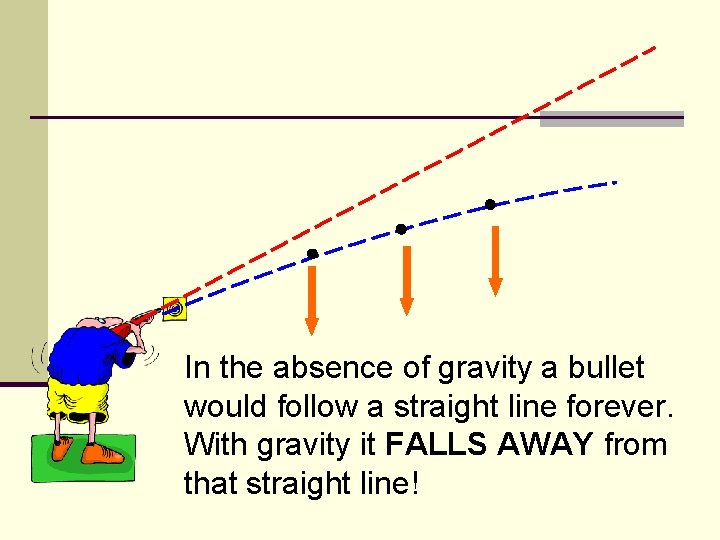
In the absence of gravity a bullet would follow a straight line forever. With gravity it FALLS AWAY from that straight line!

Football without gravity and with…

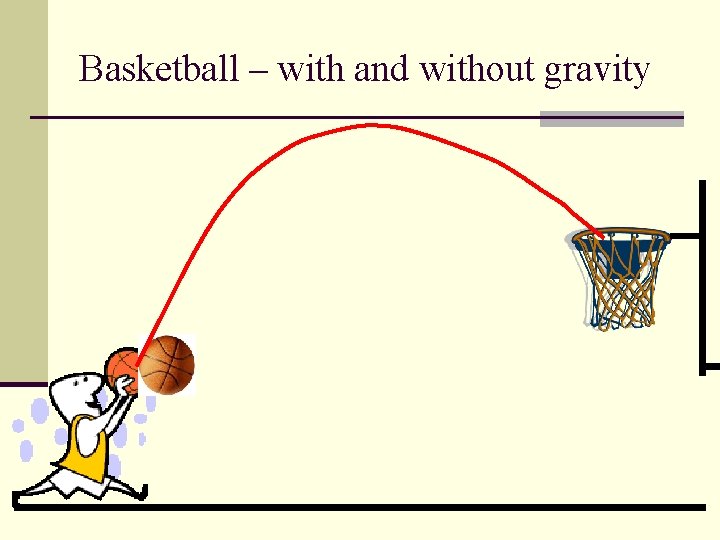
Basketball – with and without gravity

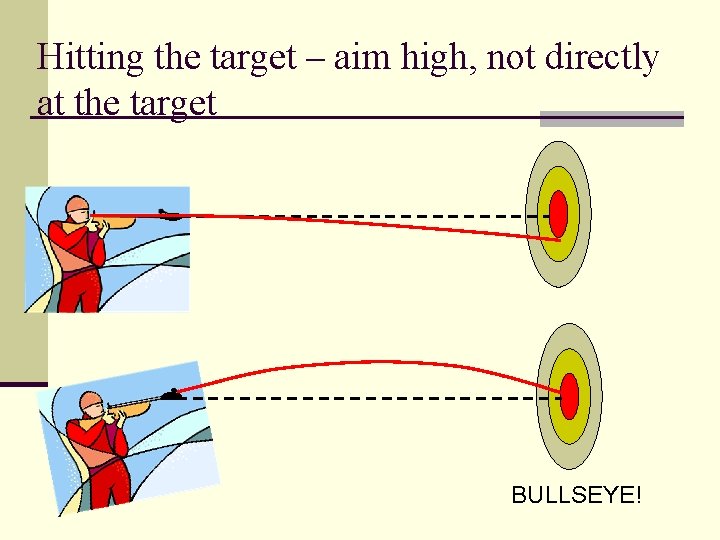
Hitting the target – aim high, not directly at the target BULLSEYE!

Projectile Examples These are all examples of things that are projected, then go off under the influence of gravity n n n Tennis ball Golf ball Football Softball Soccer ball Bullet n Hockey puck n Basketball n Volleyball n Arrow n Shot put n Javelin

Not projectiles n Jet plane n Rocket n Car (unless it looses contact with ground) Why are these things NOT projectiles?

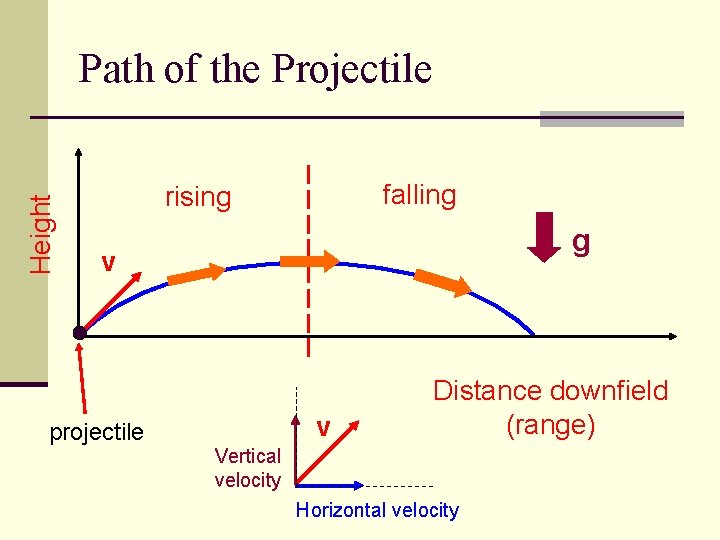
Height Path of the Projectile falling rising g v projectile v Distance downfield (range) Vertical velocity Horizontal velocity

The key to understanding projectile motion is to realize that gravity acts vertically it affects only the vertical part of the motion, not the horizontal part of the motion

Vectors first, then the path… n In order to describe the motion of objects like this, we have to learn about the initial vectors FIRST. n After that we will learn how to calculate: How high… n How far … n How long … n How fast… n

Vectors at an angle… X component y component Ve ct component and a y-component. n Finding the components of a 2 -D vector is called RESOLVING the vector n To find the values of these components, we use trigonometry. or n A vector in 2 -D is made of an x-

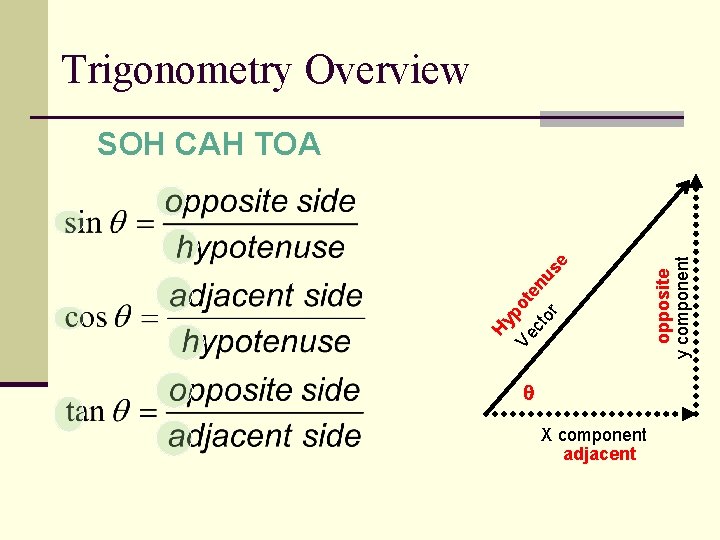
Trigonometry Overview X component adjacent opposite y component Hy Ve pot ct en us or e SOH CAH TOA

Example: Resolving a Vector Write this example in your comp book p. 25 n A football is kicked with an initial velocity of 15 m/s at 30º above the horizon. What are the xand y-components? Resolving a vector: • Label parts of triangle. • Choose a trig function for the missing information. • Use your calculator. Vx = 15 cos 30 = 13 m/s Vy = 15 sin 30 = 7. 5 m/s

Using components to make a 2 -D vector X component y component Ve ct component and a y-component. n When the vectors occur in ONE dimension, you can just add/subtract. n But when you combine vectors in 2 -D, you have to use trig… or n A vector in 2 -D is made of an x-

Using components to make a 2 -D vector n Let the x- and y-components be the AND… determine the MAGNITUDE: n a 2+ b 2 = c 2 n Use tangent to determine the DIRECTION (the angle). Ve ct n Use Pythagorean theorem to or n It’s the RESULTANT vector. X component y component sides of a right triangle. n Draw a diagonal line. This is the hypotenuse of the right triangle

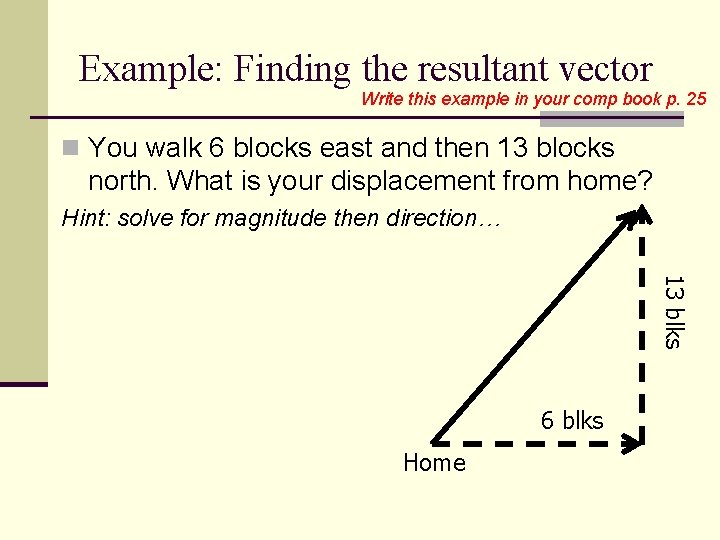
Example: Finding the resultant vector Write this example in your comp book p. 25 n You walk 6 blocks east and then 13 blocks north. What is your displacement from home? Hint: solve for magnitude then direction… 13 blks 6 blks Home

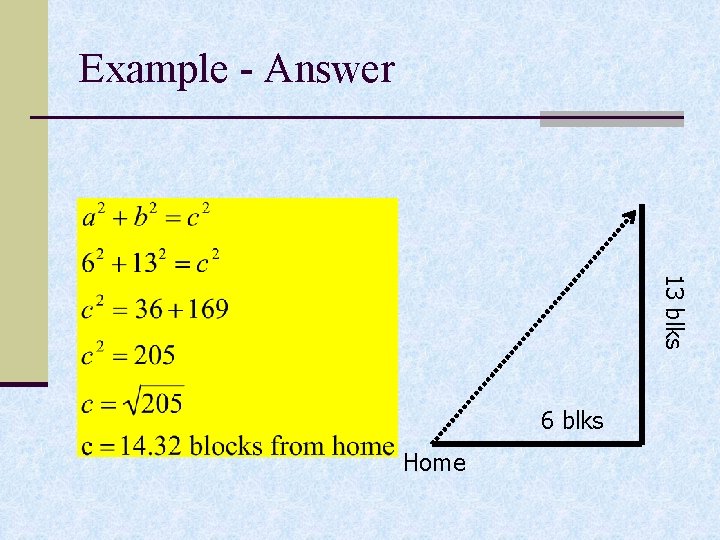
Example - Answer 13 blks 6 blks Home

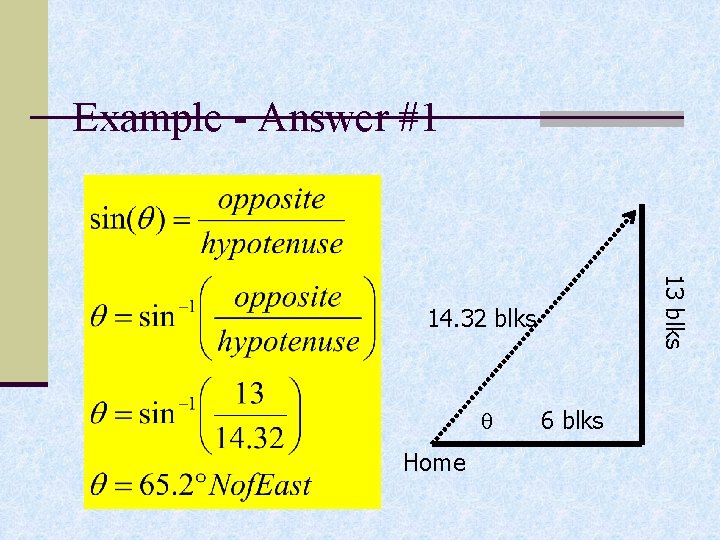
Example - Answer #1 13 blks 14. 32 blks Home 6 blks

Demonstration n We can see that the horizontal and vertical motions are independent n The red ball falls vertically n The yellow ball was given a kick to the right. n They track each other vertically step for step and hit the ground at the same time

Projectile motion – key points 1) The projectile has both a vertical and horizontal component of velocity 2) The only force acting on the projectile once it is shot is gravity (neglecting air resistance) 3) At all times the acceleration of the projectile is g = - 9. 8 m/s 2 (downward) 4) The horizontal velocity of the projectile does not change throughout the path

Key points, continued 5) On the rising portion of the path, gravity causes the vertical component of velocity to get smaller and smaller 6) At the very top of the path, the vertical component of velocity is ZERO 7) On the falling portion of the path, the vertical velocity increases

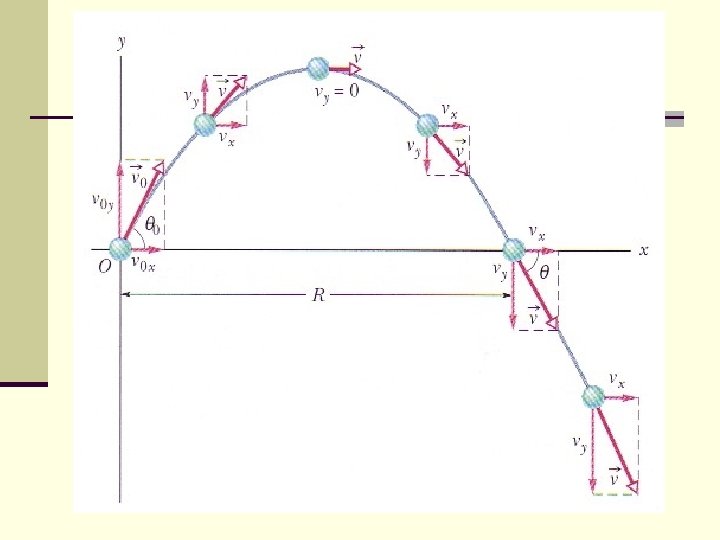
More key points 8) If the projectile lands at the same elevation as its starting point, it will have the same final vertical SPEED as initial (opposite velocity) 9) The time it takes to get to the top of its path is the same as the time to get from the top back to the ground. 10) The range of the projectile (where it lands) depends on its initial speed angle of elevation

Example: A 2. 00 m tall basketball player wants to make a basket from a distance of 10. 0 m. If he shoots the ball at a 450 angle, at what initial speed must he throw the ball so that it goes through the hoop without striking the backboard? y y 0 x

Maximum Range n When an artillery shell is fired the initial speed of the projectile depends on the explosive charge – this cannot be changed n The only control you have is over the angle of elevation. n You can control the range (where it lands) by changing the angle of elevation n To get maximum range set the angle to 45°

Interactive n http: //galileo. phys. virginia. edu/classes/109 N/ more_stuff/Applets/Projectile. Motion/jarapplet. html n http: //jersey. uoregon. edu/vlab/Cannon/

The ultimate projectile: Putting an object into orbit • Imagine trying to throw a rock around the world. • If you give it a large horizontal velocity, it will go into orbit around the earth!