Unit 4 TRIANGLE FUN I Ican canuse usethe





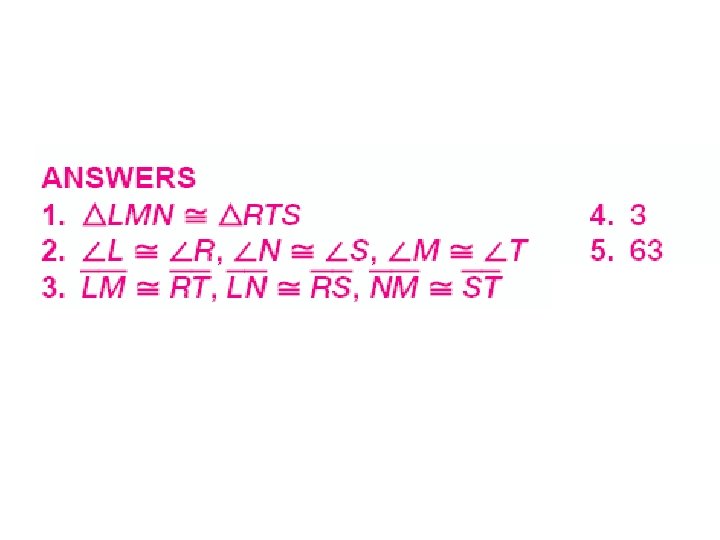












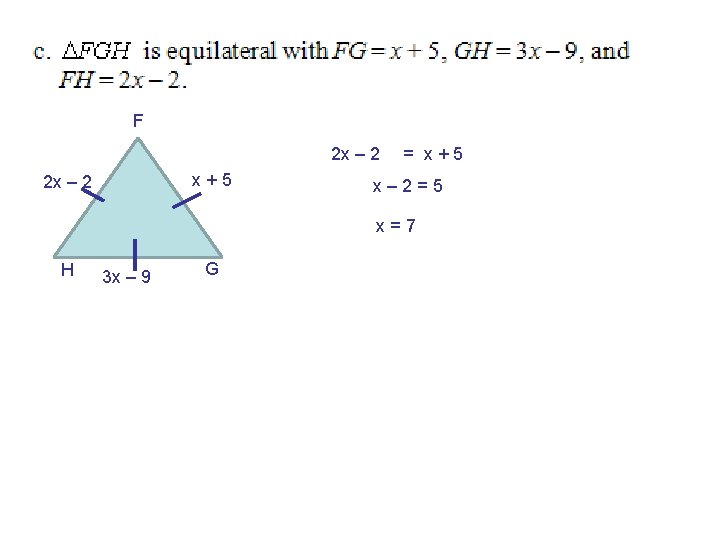


- Slides: 66

Unit 4 TRIANGLE FUN

• • I Ican canuse usethe theanglesum theorem • I can the exterior angle theorem Learning Targets Lesson 4 -1

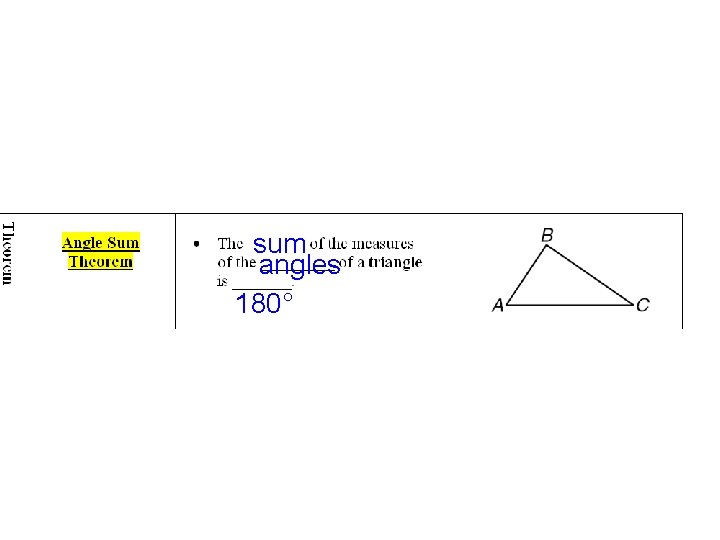
sum angles 180°

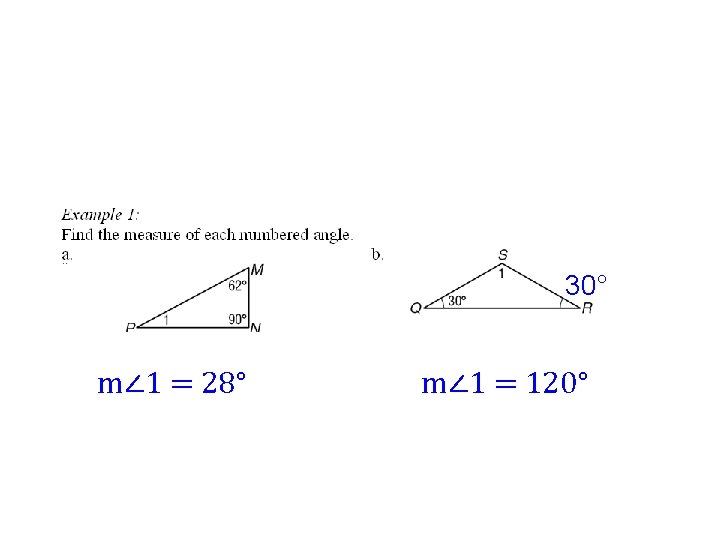
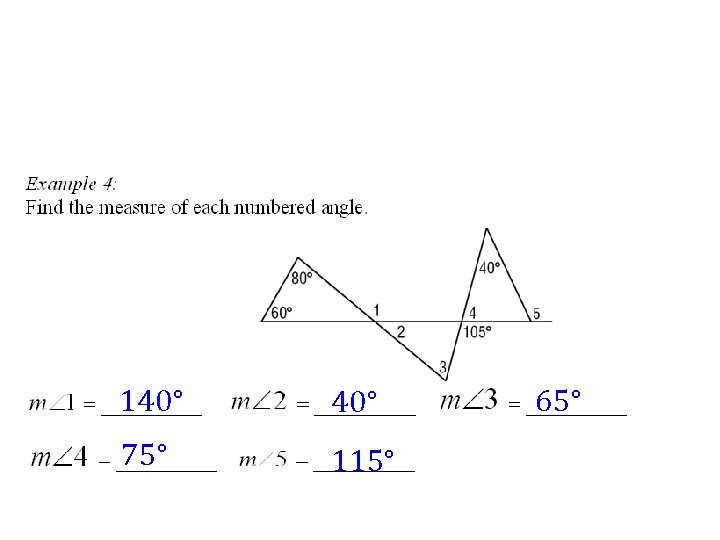
30° m∠ 1 = 28° m∠ 1 = 120°

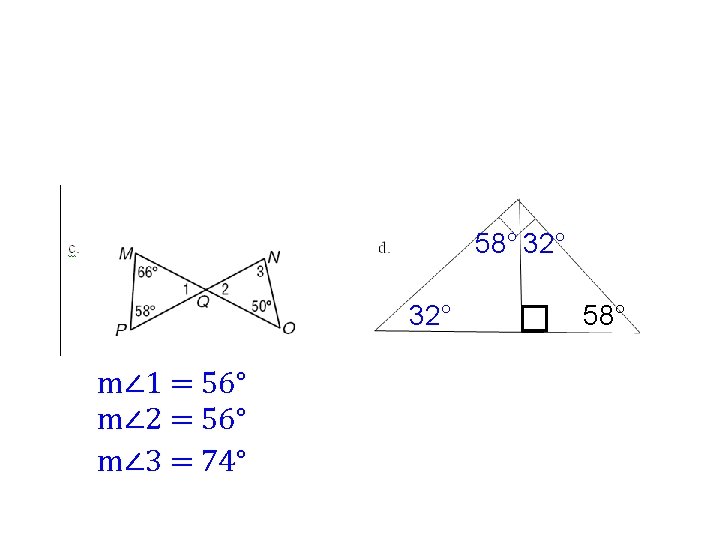
58° 32° m∠ 1 = 56° m∠ 2 = 56° m∠ 3 = 74° 58°

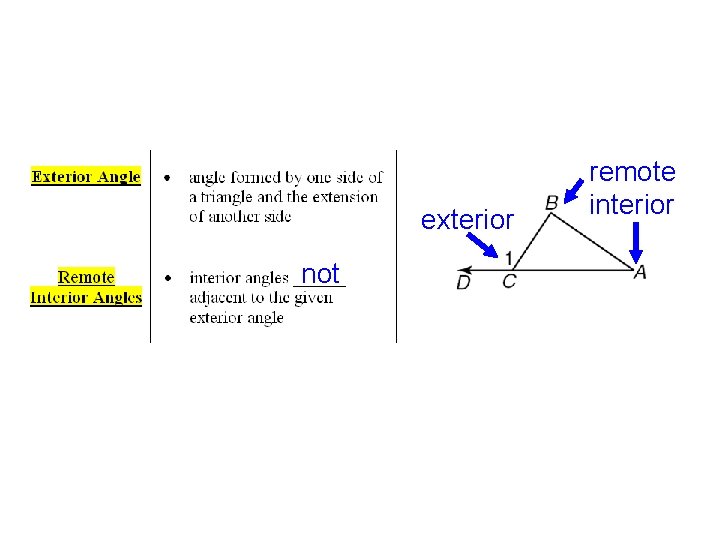
exterior not remote interior

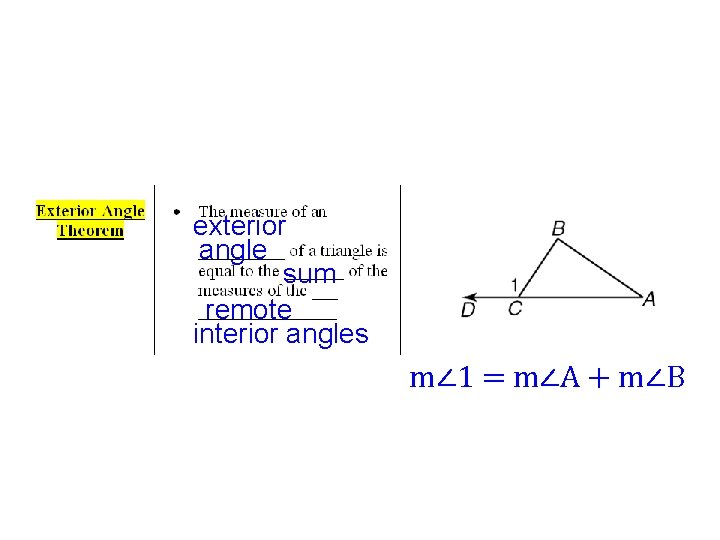
exterior angle sum remote interior angles m∠ 1 = m∠A + m∠B

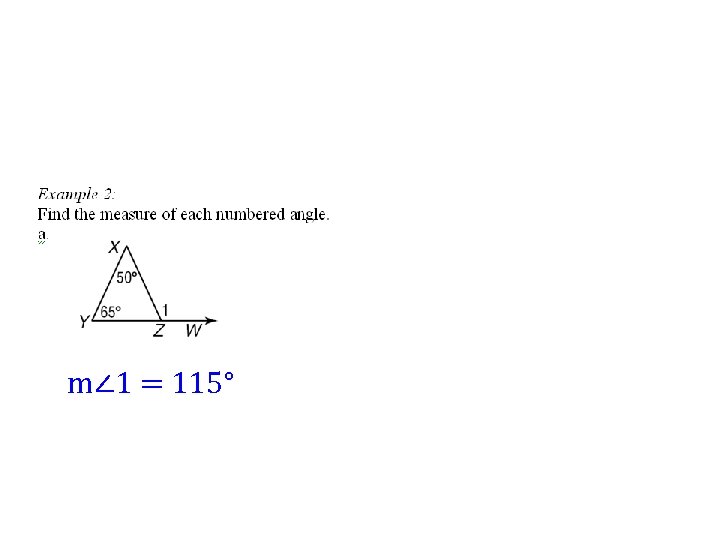
m∠ 1 = 115°

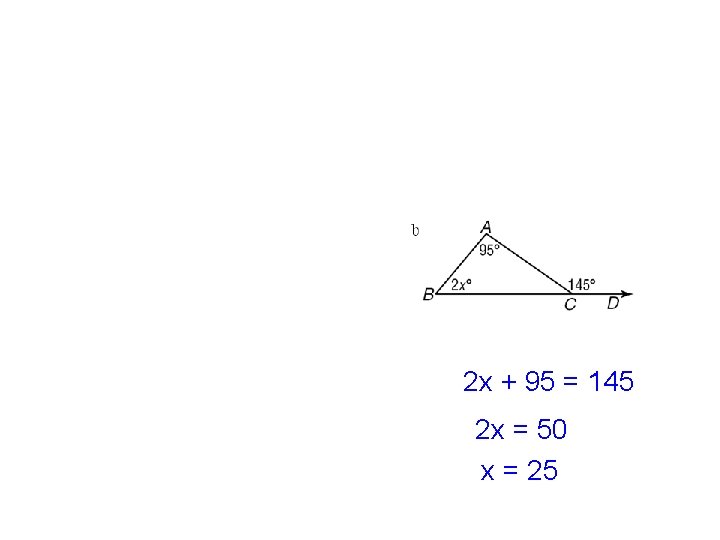
2 x + 95 = 145 2 x = 50 x = 25

140° 75° 115° 65°

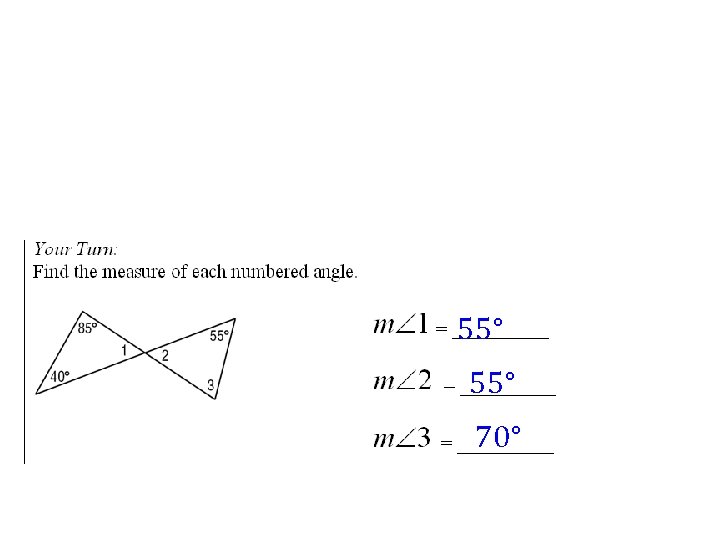
55° 70°

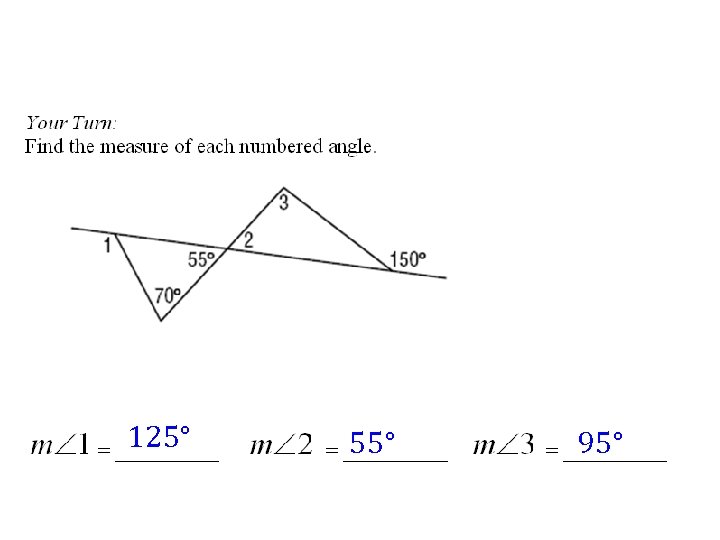
125° 55° 95°

ASSIGNMENT: 4 -1 Worksheet

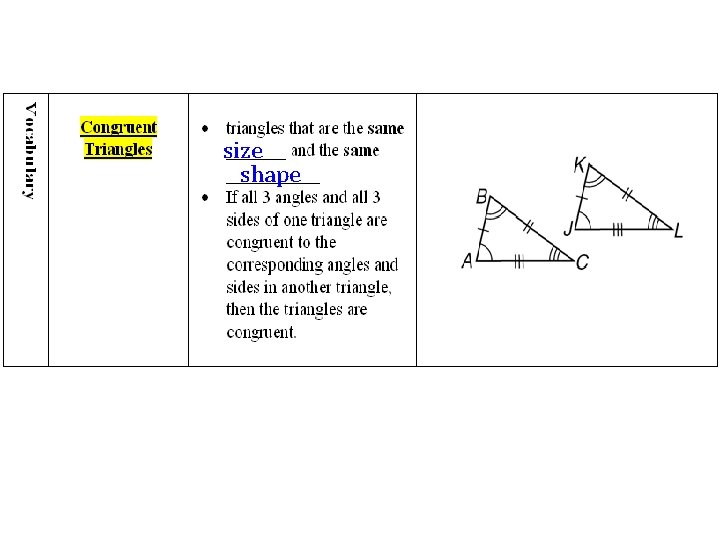
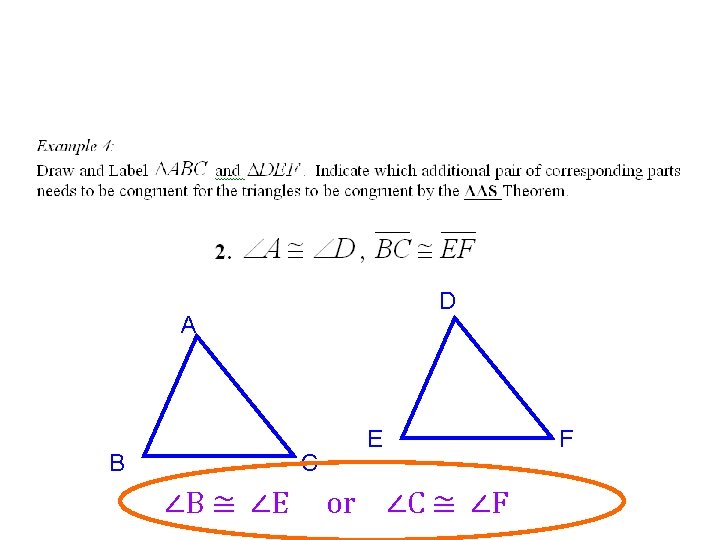
4. 2 Congruent Triangles Learning Target: • I can name and label corresponding parts of congruent triangles.

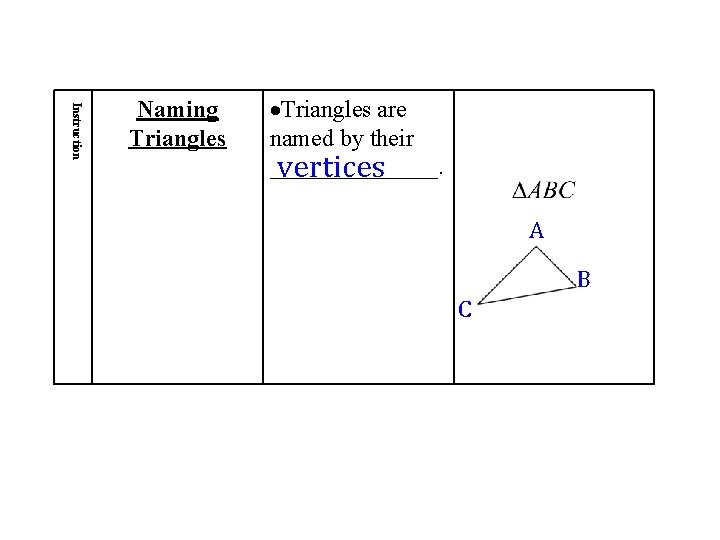
Instruction Naming Triangles are named by their _______. vertices A B C

size shape

Angle Measure Betweenness Collinearity Distance

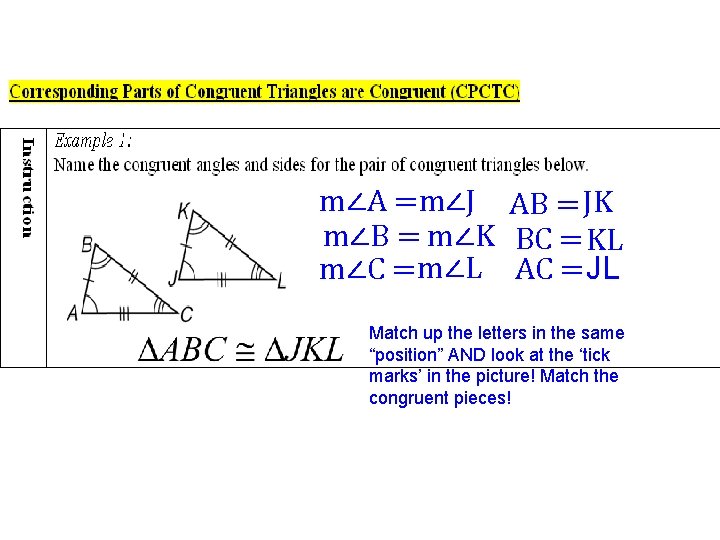
m∠A =m∠J AB = JK m∠B = m∠K BC = KL m∠C = m∠L AC = JL Match up the letters in the same “position” AND look at the ‘tick marks’ in the picture! Match the congruent pieces!



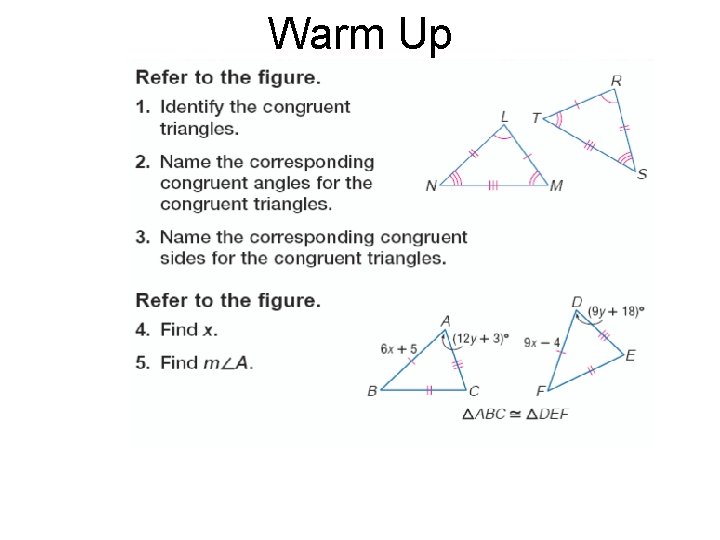
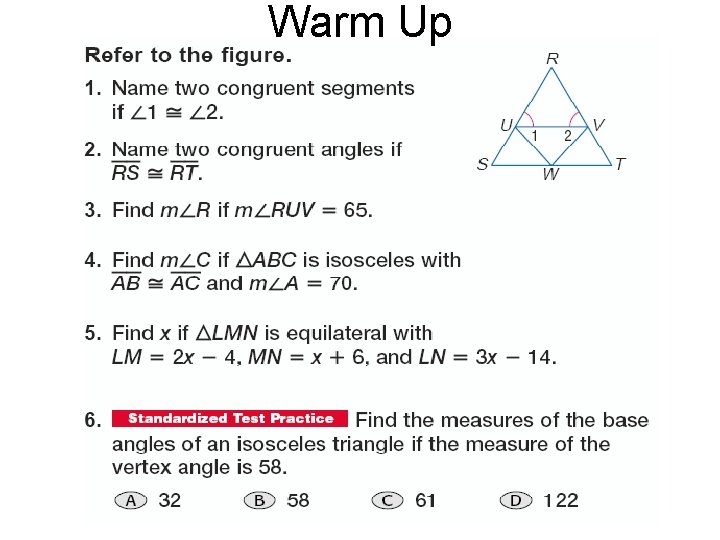
Warm Up


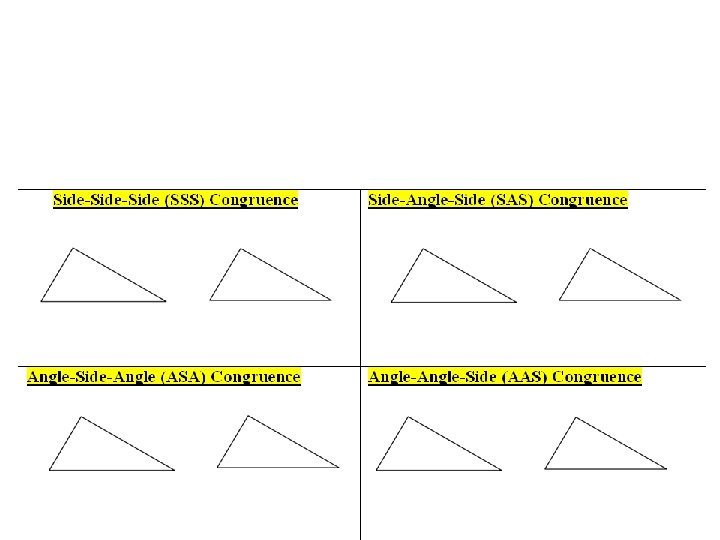
• I can recognize and use the SSS, SAS, ASA, AAS, and HL Postulates to see if triangles are the same. Lesson 4. 3


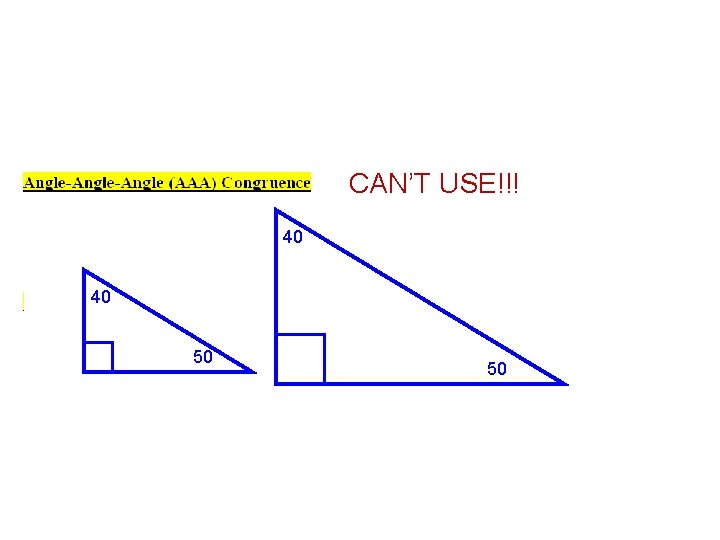
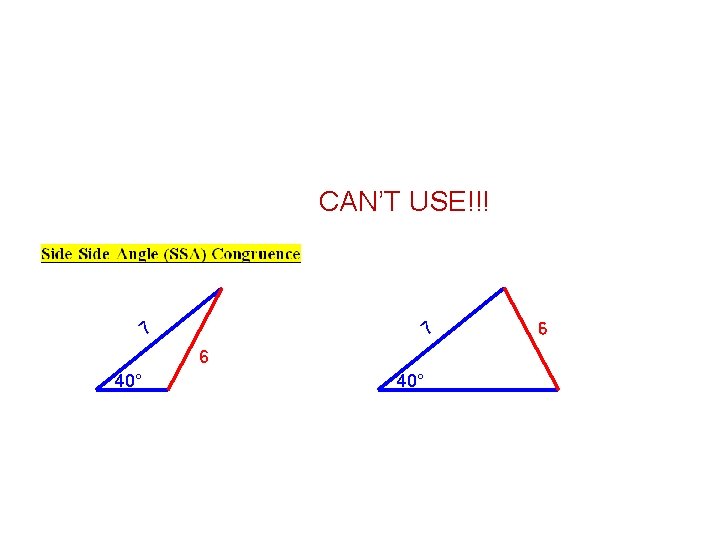
CAN’T USE!!! 40 40 50 50

CAN’T USE!!! 7 7 6 40° 6


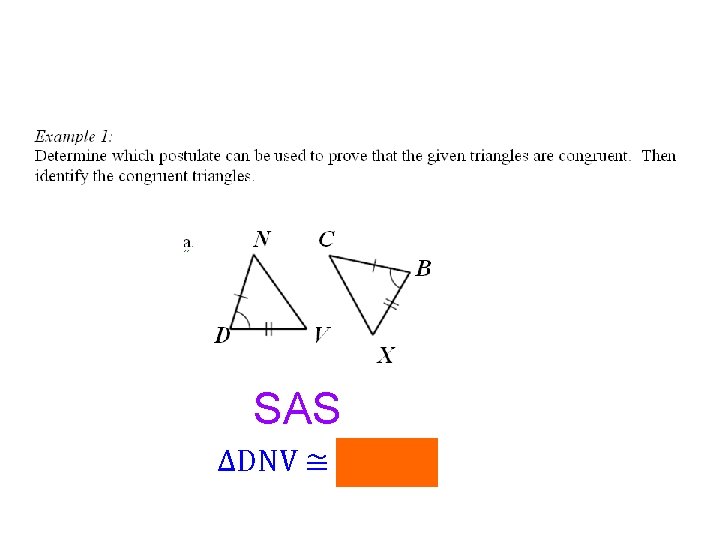
SAS ∆DNV ≅ ∆BCX

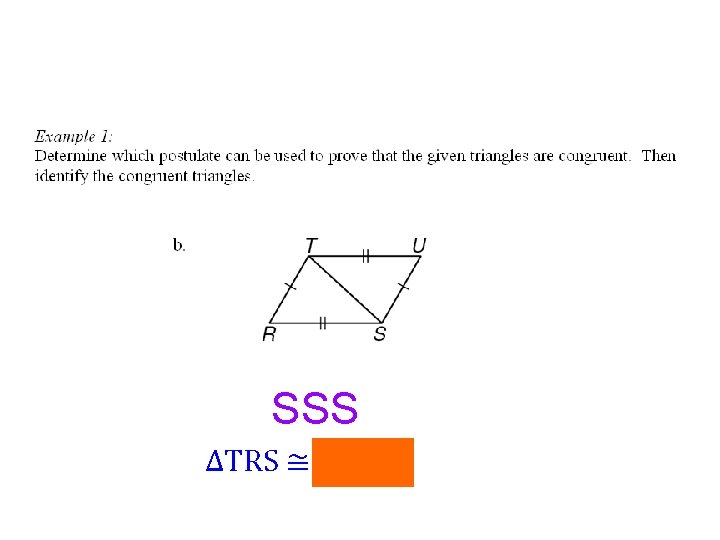
SSS ∆TRS ≅ ∆SUT

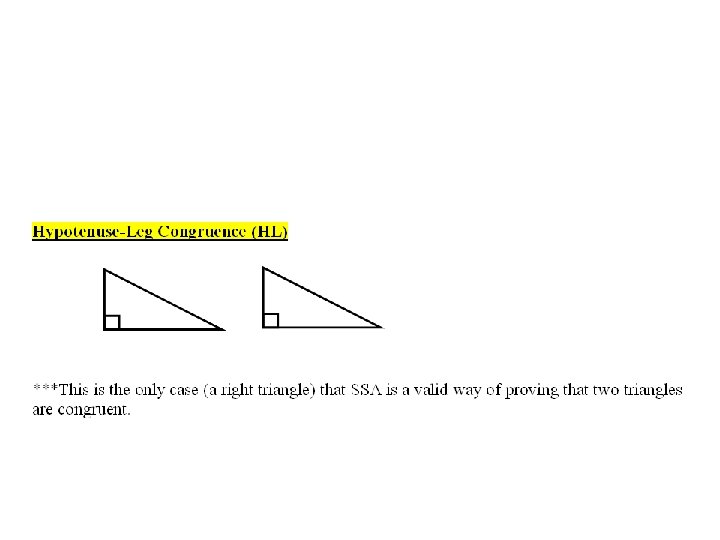
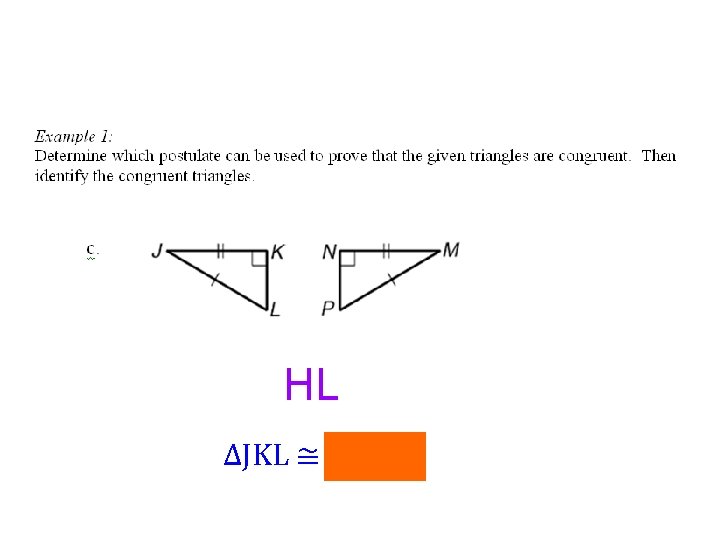
HL ∆JKL ≅ ∆MNP

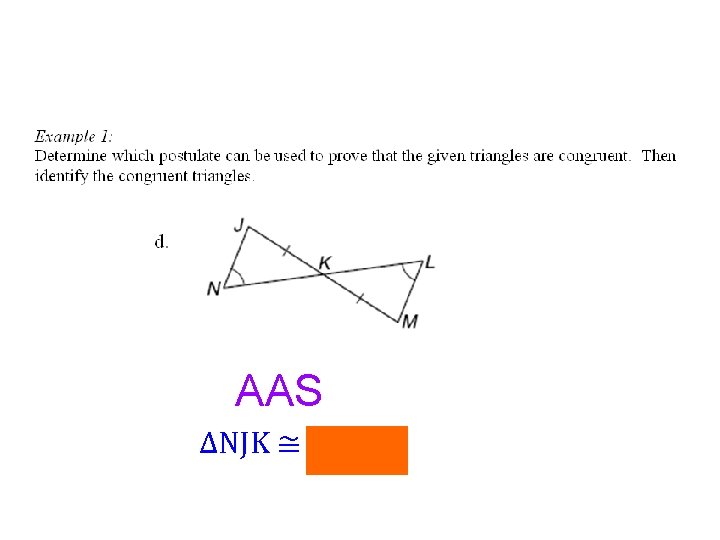
AAS ∆NJK ≅ ∆LMK

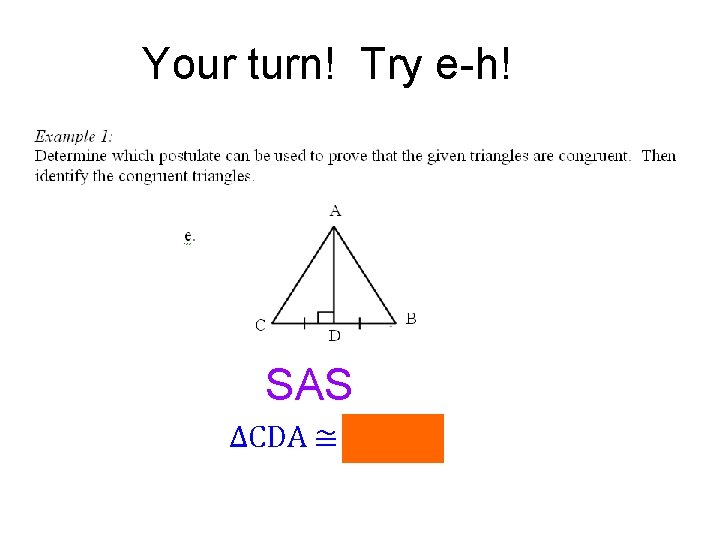
Your turn! Try e-h! SAS ∆CDA ≅ ∆BDA

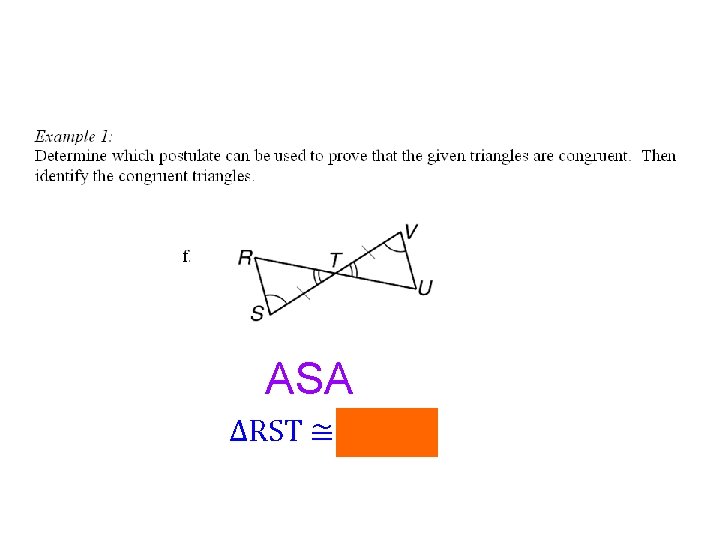
ASA ∆RST ≅ ∆UVT

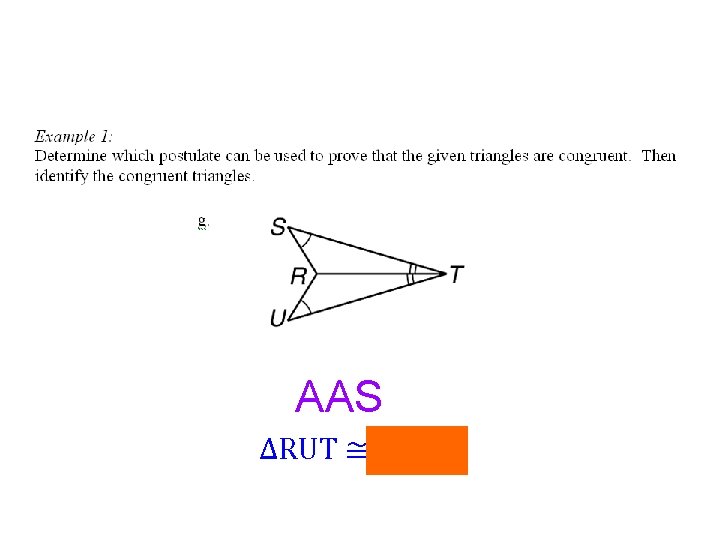
AAS ∆RUT ≅ ∆RST

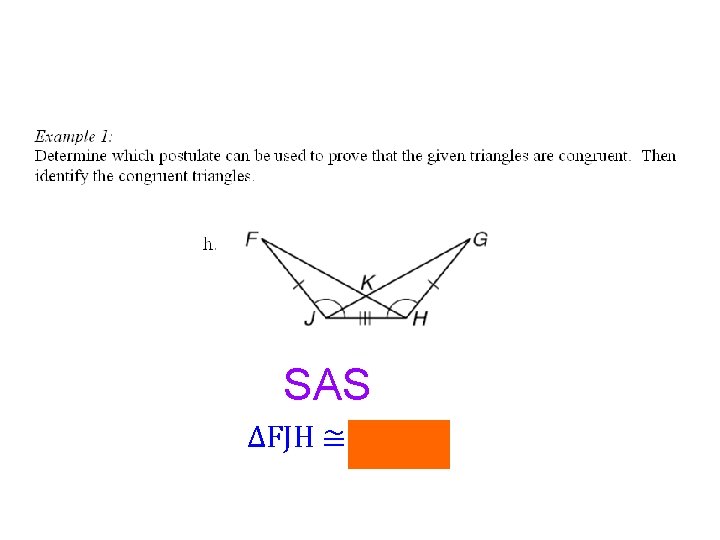
SAS ∆FJH ≅ ∆GHJ

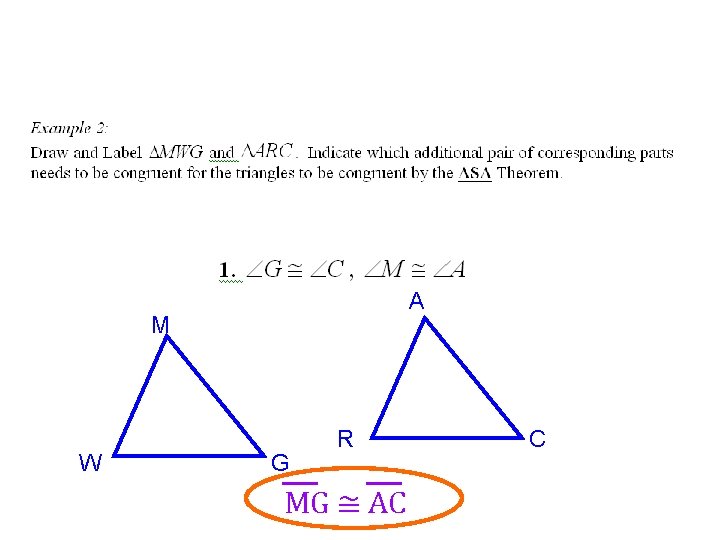
A M W G R MG ≅ AC C

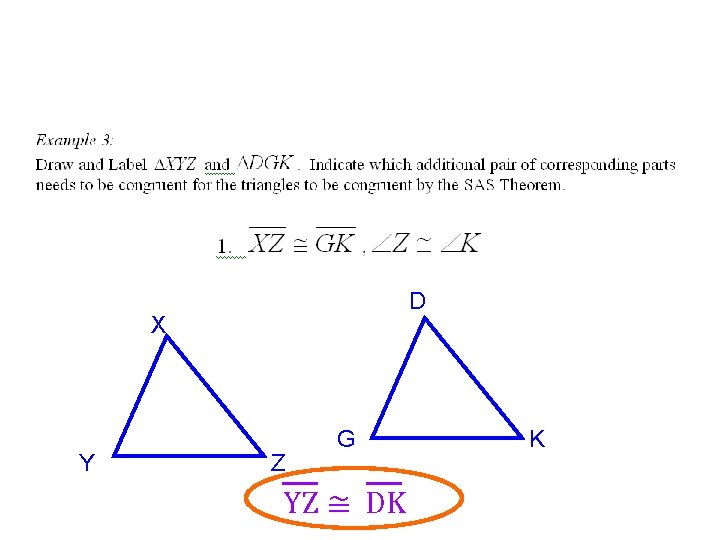
D X Y Z G YZ ≅ DK K


ASSIGNMENT: “Swimming through triangles” worksheet, both sides (Pages 3 – 4)

Warm Up


PROOFS! Lesson 4. 4

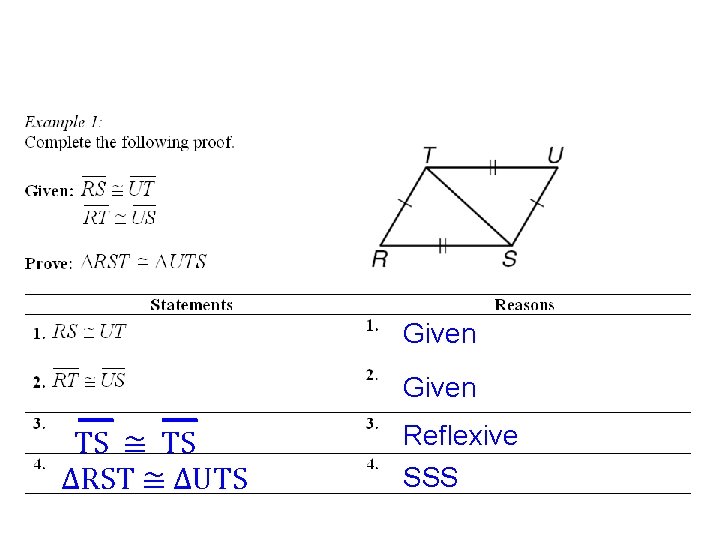
Given TS ≅ TS ∆RST ≅ ∆UTS Reflexive SSS

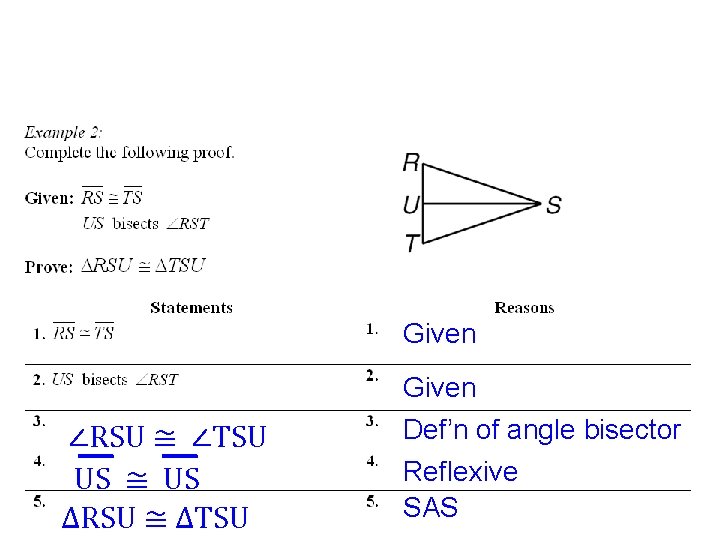
Given ∠RSU ≅ ∠TSU US ≅ US ∆RSU ≅ ∆TSU Given Def’n of angle bisector Reflexive SAS

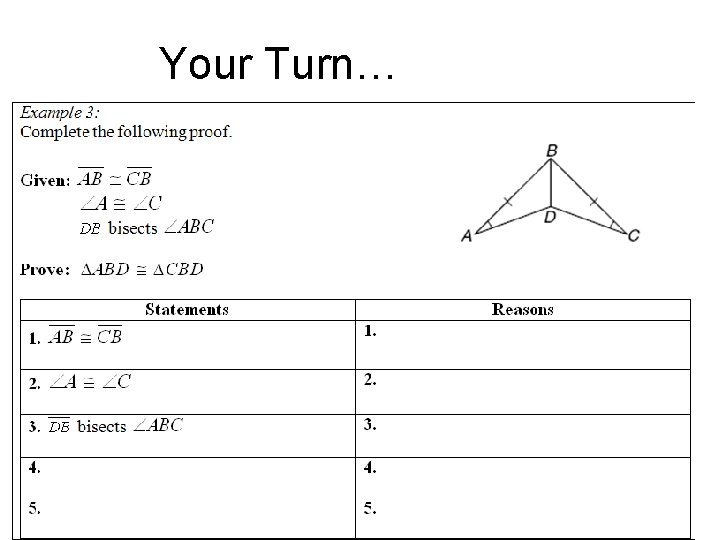
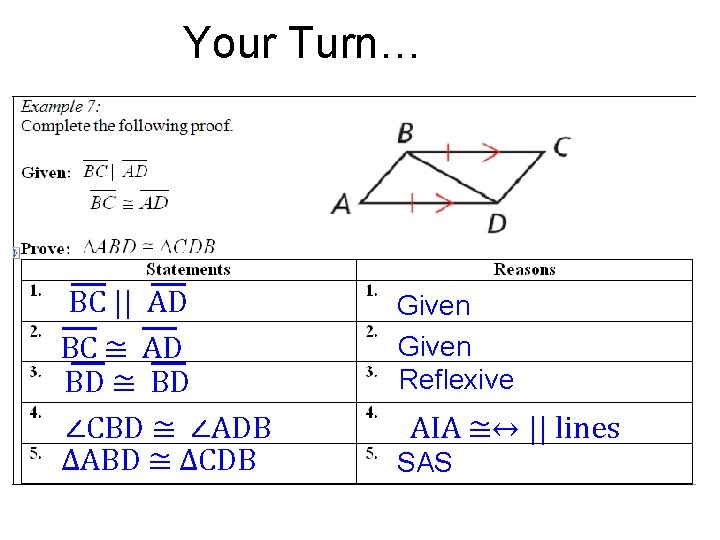
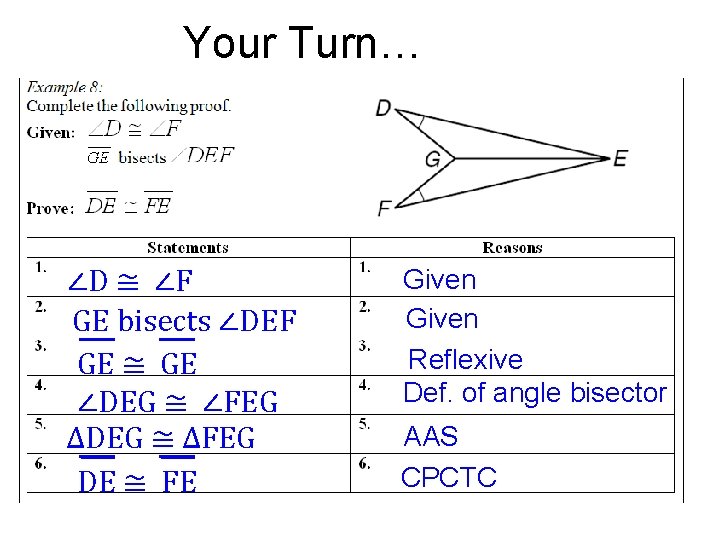
Your Turn…

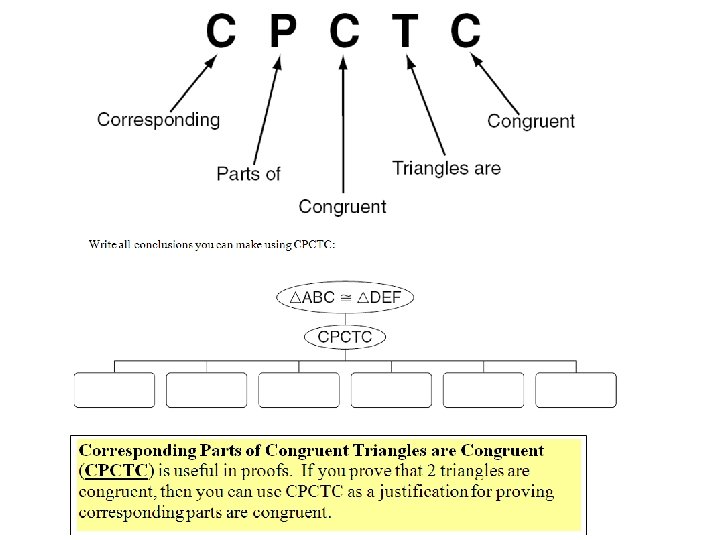
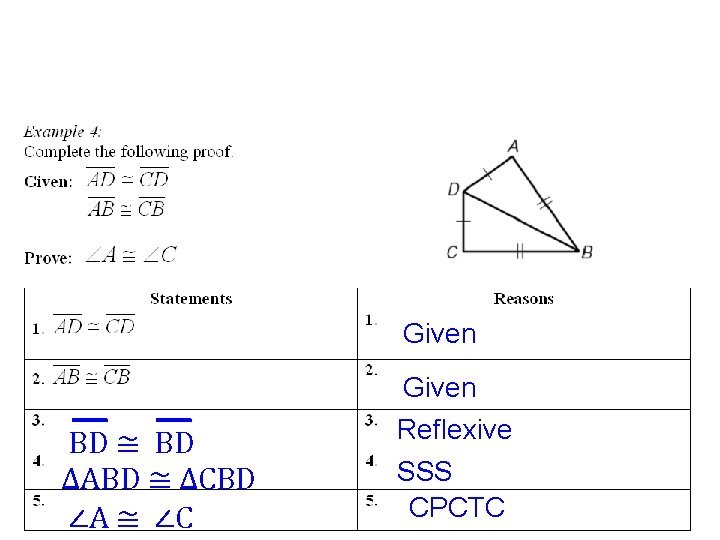
Given BD ≅ BD ∆ABD ≅ ∆CBD ∠A ≅ ∠C Given Reflexive SSS CPCTC

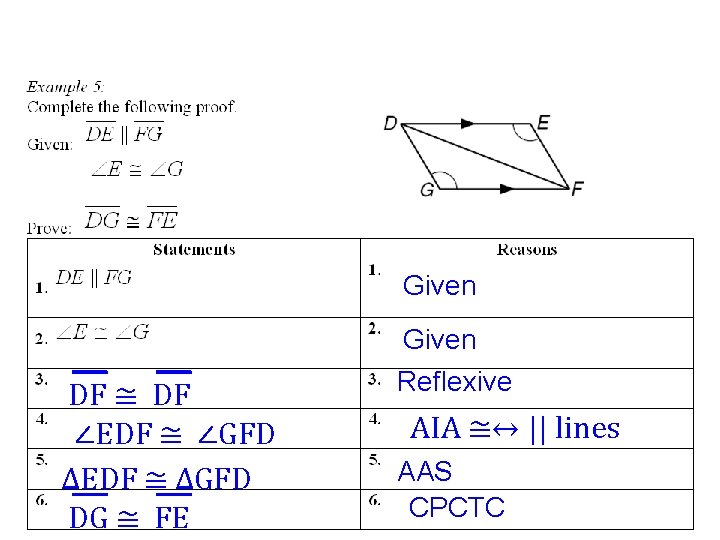
Given DF ≅ DF ∠EDF ≅ ∠GFD ∆EDF ≅ ∆GFD DG ≅ FE Given Reflexive AIA ≅↔ || lines AAS CPCTC

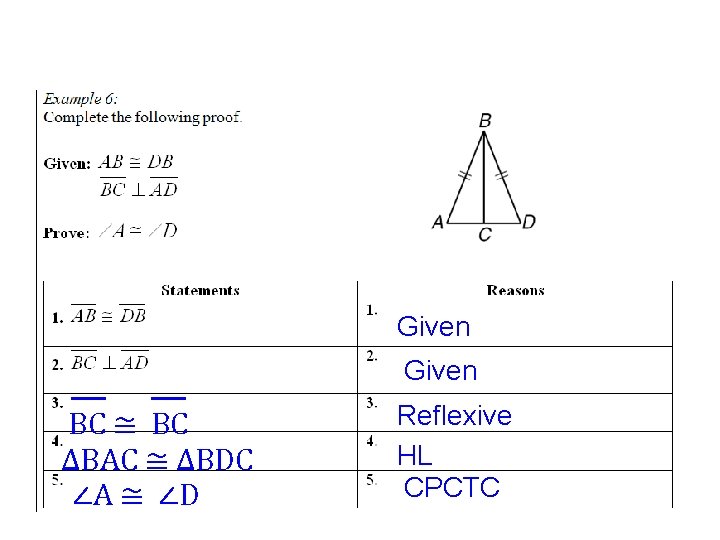
Given BC ≅ BC ∆BAC ≅ ∆BDC ∠A ≅ ∠D Reflexive HL CPCTC

Your Turn… BC || AD BC ≅ AD BD ≅ BD ∠CBD ≅ ∠ADB ∆ABD ≅ ∆CDB Given Reflexive AIA ≅↔ || lines SAS

Your Turn… ∠D ≅ ∠F GE bisects ∠DEF GE ≅ GE ∠DEG ≅ ∠FEG ∆DEG ≅ ∆FEG DE ≅ FE Given Reflexive Def. of angle bisector AAS CPCTC

Group Activity Please put your tables into groups of 4 (push 2 tables together!) We will rotate through 4 stations to fill out proofs You will have approximately 4 minutes per station. Work quickly but accurately!

Warm Up


4. 5 Isosceles and Equilateral Triangles Learning Targets • I can use properties of isosceles triangles. • I can use properties of equilateral triangles.

Vertex angle 2 congruent sides opposite 2 congruent sides Base angles

2 sides opposite congruent

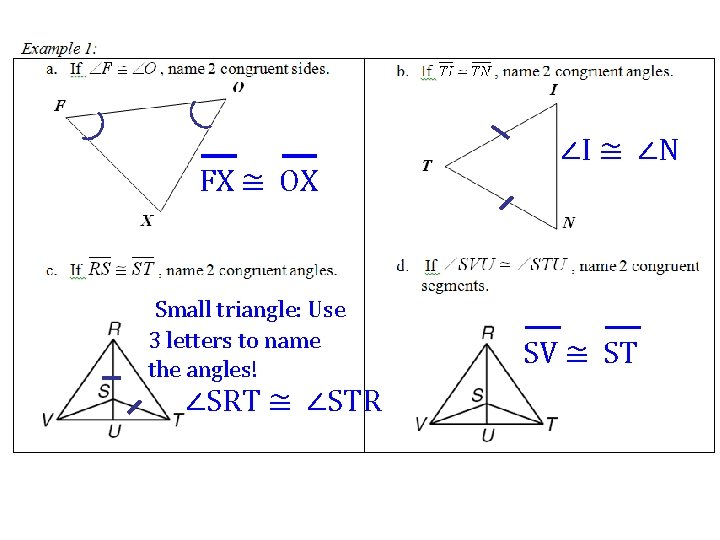
FX ≅ OX Small triangle: Use 3 letters to name the angles! ∠SRT ≅ ∠STR ∠I ≅ ∠N SV ≅ ST

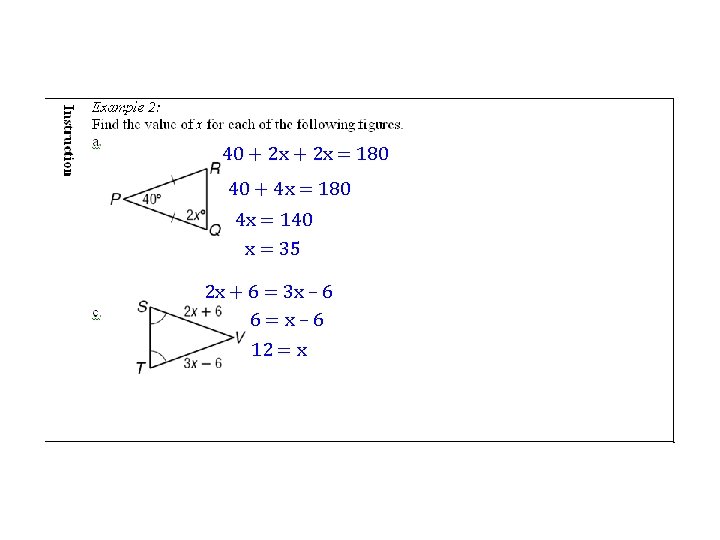
40 + 2 x = 180 40 + 4 x = 180 4 x = 140 x = 35 2 x + 6 = 3 x – 6 6=x– 6 12 = x

L 3 x – 2 2 x + 1 = 3 x – 2 1=x– 2 M N 5 x – 2 x=3

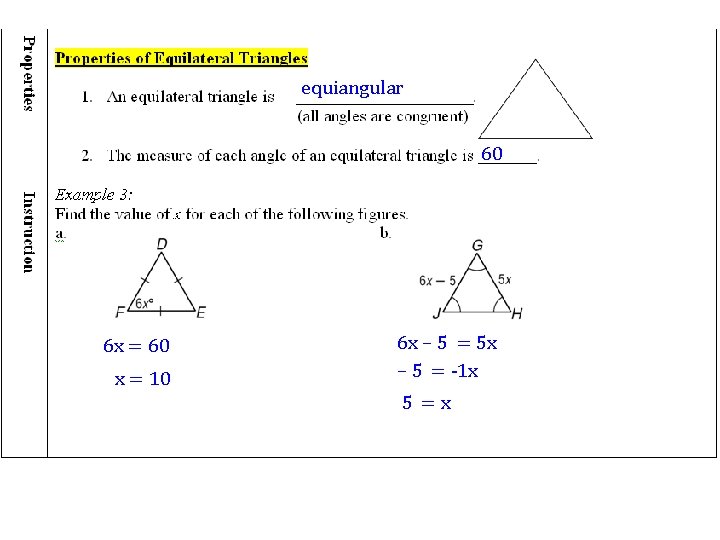
equiangular 60 6 x = 60 x = 10 6 x – 5 = 5 x – 5 = -1 x 5 =x
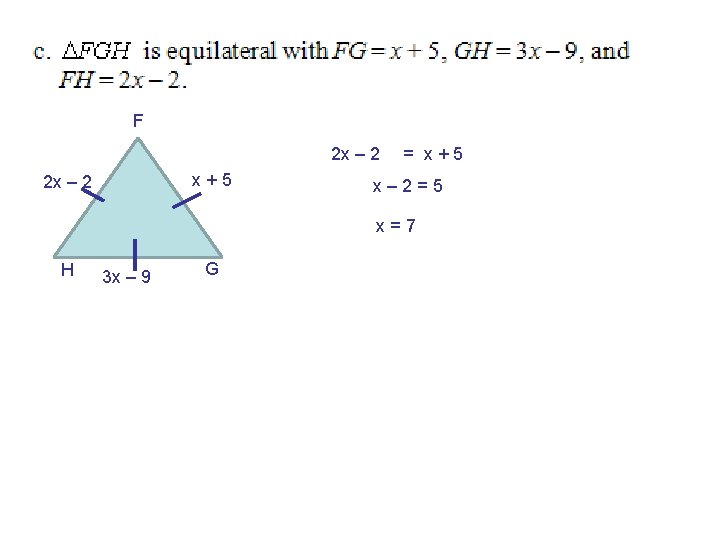
F 2 x – 2 x+5 2 x – 2 = x+5 x– 2=5 x=7 H 3 x – 9 G

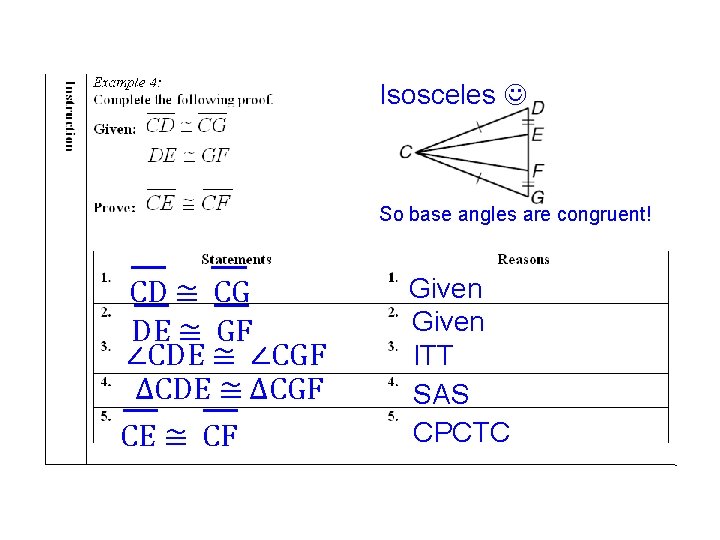
Isosceles So base angles are congruent! CD ≅ CG DE ≅ GF ∠CDE ≅ ∠CGF ∆CDE ≅ ∆CGF CE ≅ CF Given ITT SAS CPCTC

Warm Up


4. 6 Constructing Triangles Use the construction instructions to work through the constructions at your table. Please raise your hand if you need assistance!