Unit 4 Lesson 1 Apply Triangle Sum Properties





- Slides: 26

Unit 4 – Lesson 1 Apply Triangle Sum Properties And Angle Relationships

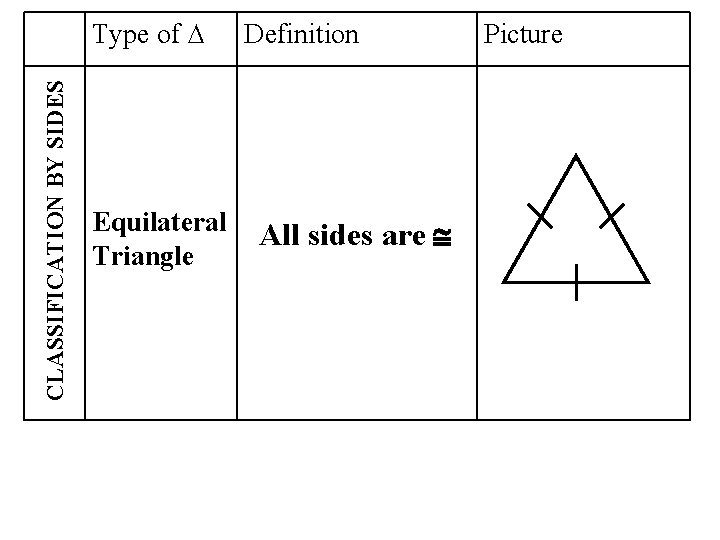
CLASSIFICATION BY SIDES Type of ∆ Equilateral Triangle Definition All sides are Picture

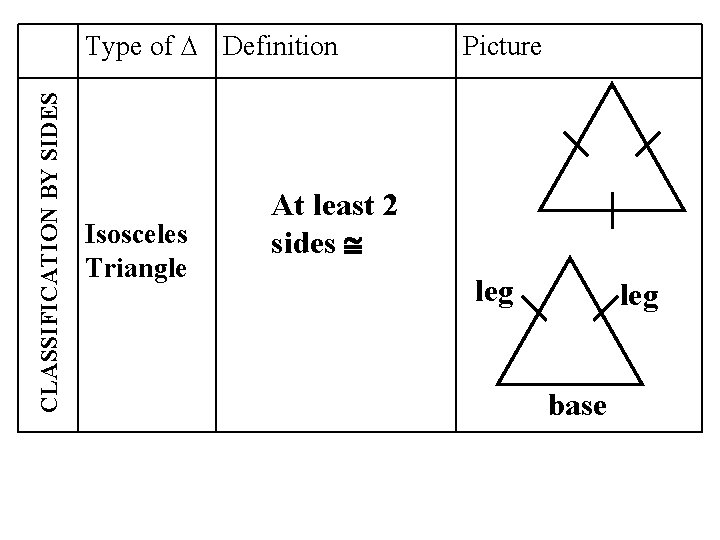
CLASSIFICATION BY SIDES Type of ∆ Definition Isosceles Triangle Picture At least 2 sides leg base

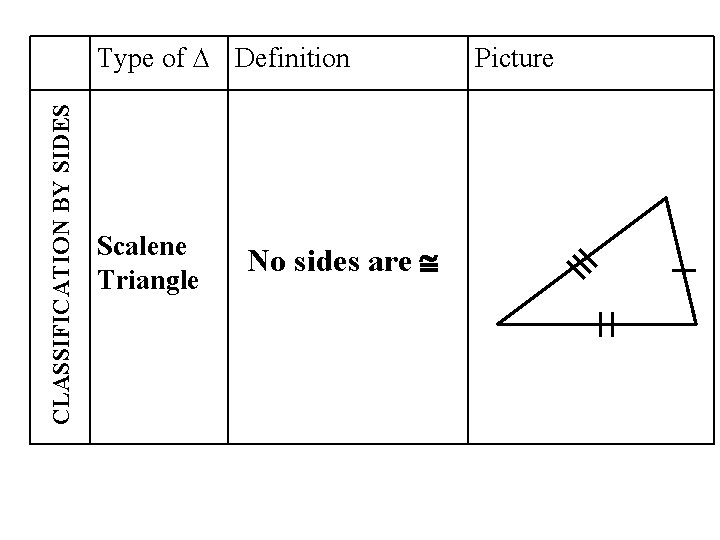
CLASSIFICATION BY SIDES Type of ∆ Definition Scalene Triangle No sides are Picture

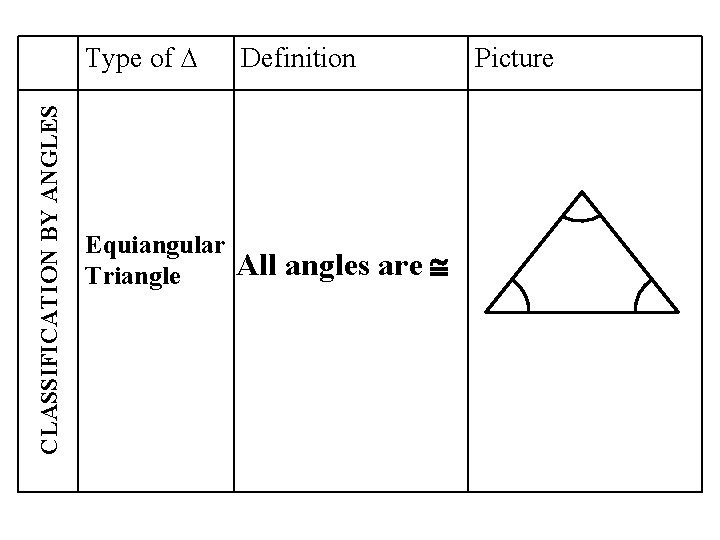
CLASSIFICATION BY ANGLES Type of ∆ Definition Equiangular Triangle All angles are Picture

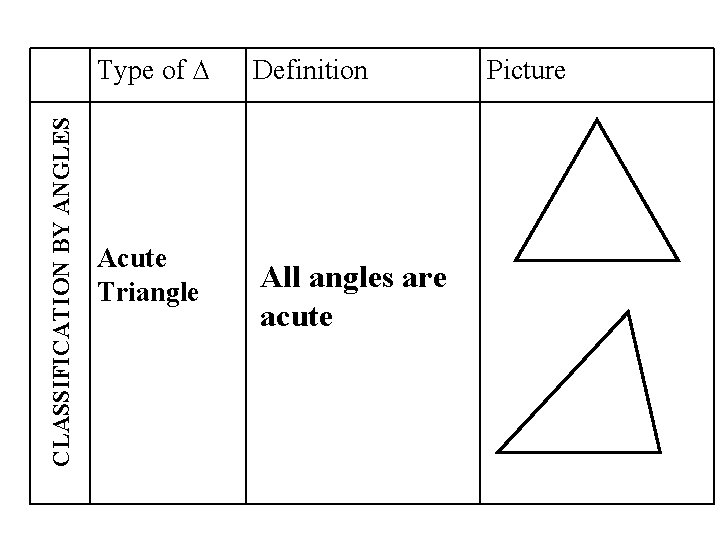
CLASSIFICATION BY ANGLES Type of ∆ Acute Triangle Definition All angles are acute Picture

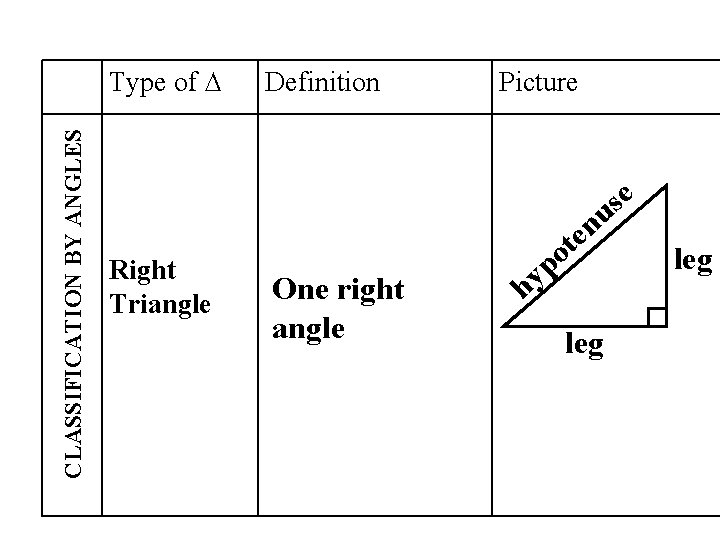
CLASSIFICATION BY ANGLES Type of ∆ Definition Picture e s u Right Triangle n e t One right angle o p y h leg

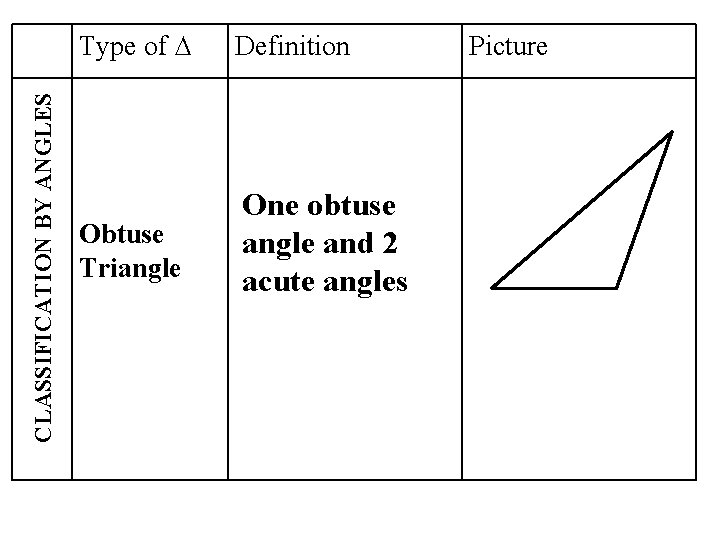
CLASSIFICATION BY ANGLES Type of ∆ Definition Obtuse Triangle One obtuse angle and 2 acute angles Picture

Interior Angles – Angles inside a shape Exterior Angles – Angles outside a shape Corollary – Statement easily proved from another statement

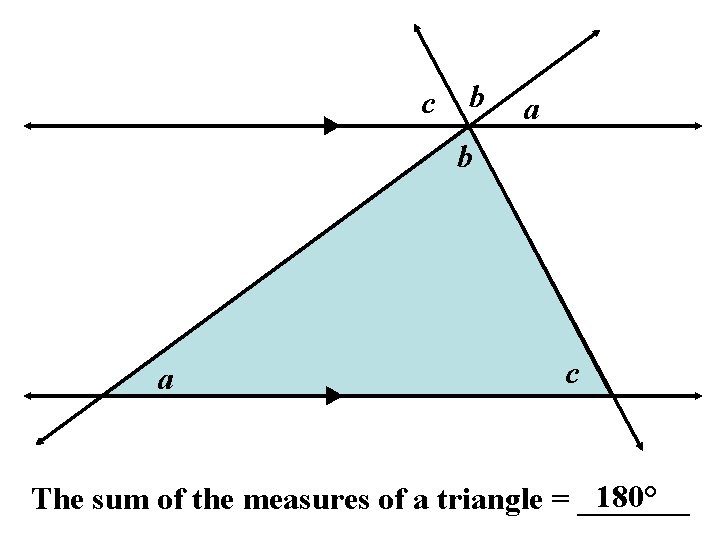
c b a c 180° The sum of the measures of a triangle = _______

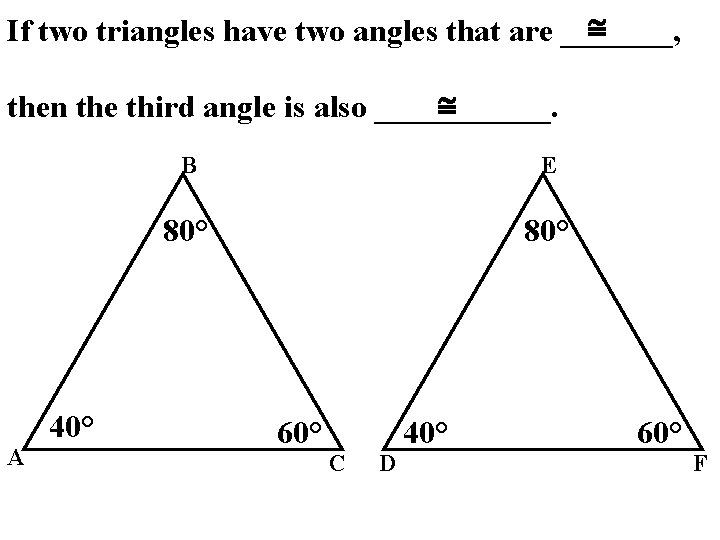
If two triangles have two angles that are _______, then the third angle is also ______. A 40° B E 80° 60° C D 40° 60° F

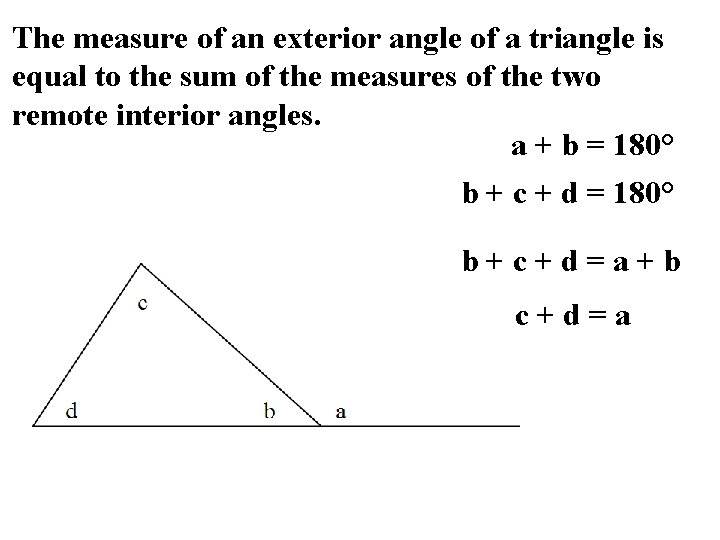
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles. a + b = 180° b + c + d = 180° b+c+d=a+b c+d=a

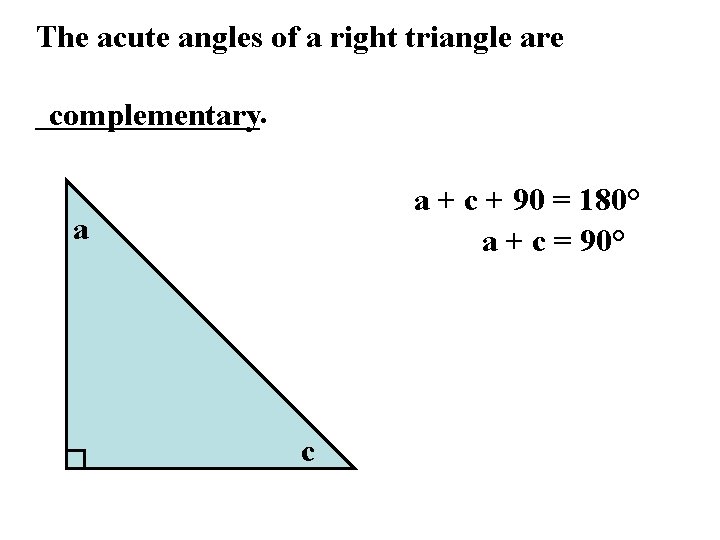
The acute angles of a right triangle are _______. complementary a + c + 90 = 180° a + c = 90° a c

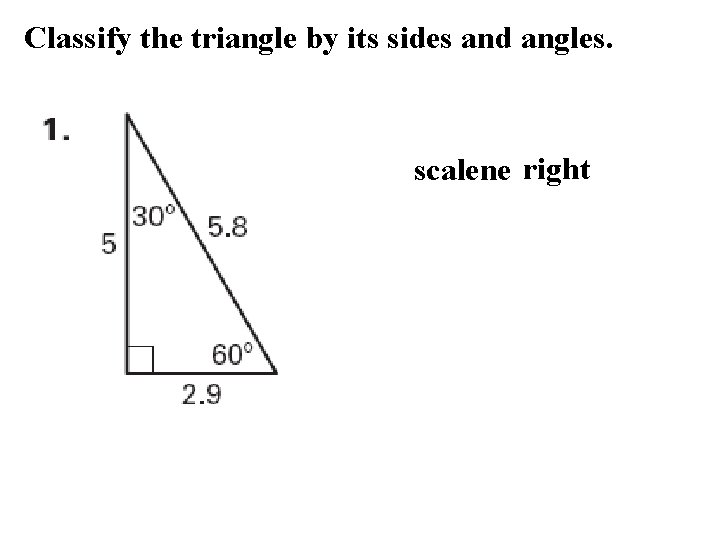
Classify the triangle by its sides and angles. scalene right

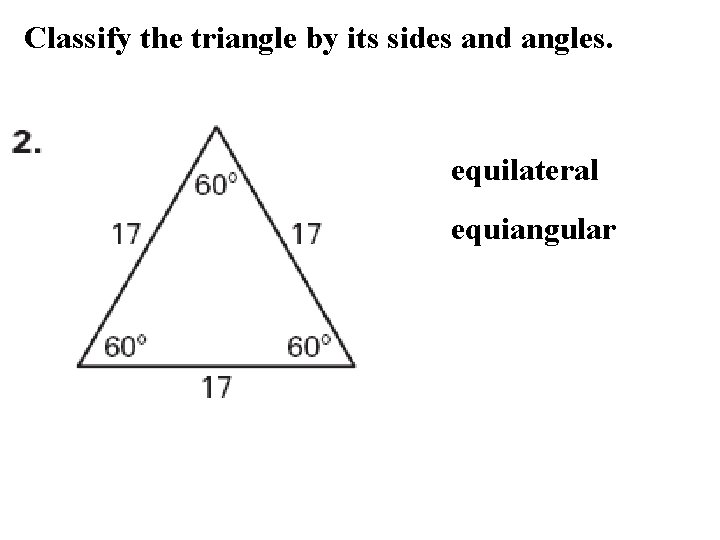
Classify the triangle by its sides and angles. equilateral equiangular

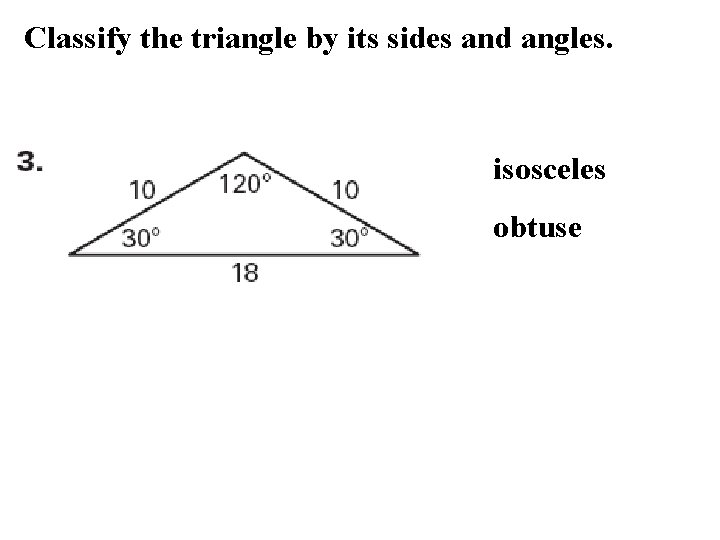
Classify the triangle by its sides and angles. isosceles obtuse

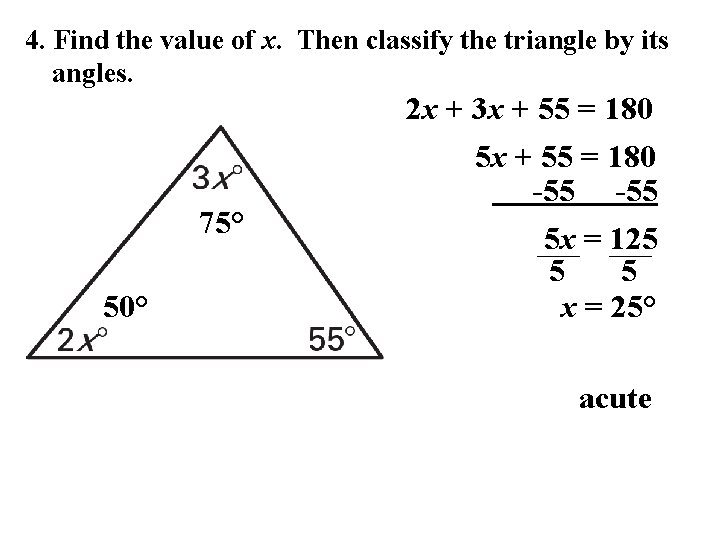
4. Find the value of x. Then classify the triangle by its angles. 2 x + 3 x + 55 = 180 75° 50° 5 x + 55 = 180 -55 5 x = 125 5 5 x = 25° acute

4. Find the value of x. Then classify the triangle by its angles. 4 x – 5 + 3 x + 5 + 40 = 180 75° 65° acute 7 x + 40 = 180 -40 7 x = 140 7 7 x = 20°

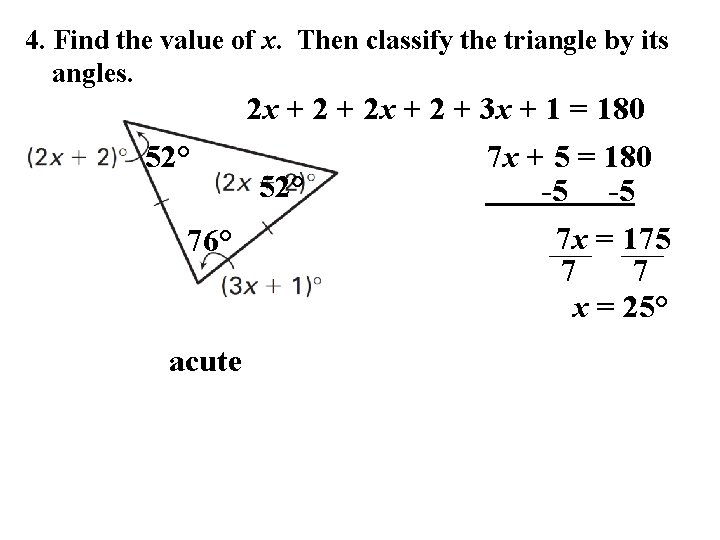
4. Find the value of x. Then classify the triangle by its angles. 2 x + 2 + 3 x + 1 = 180 52° 76° acute 52° 7 x + 5 = 180 -5 -5 7 x = 175 7 7 x = 25°

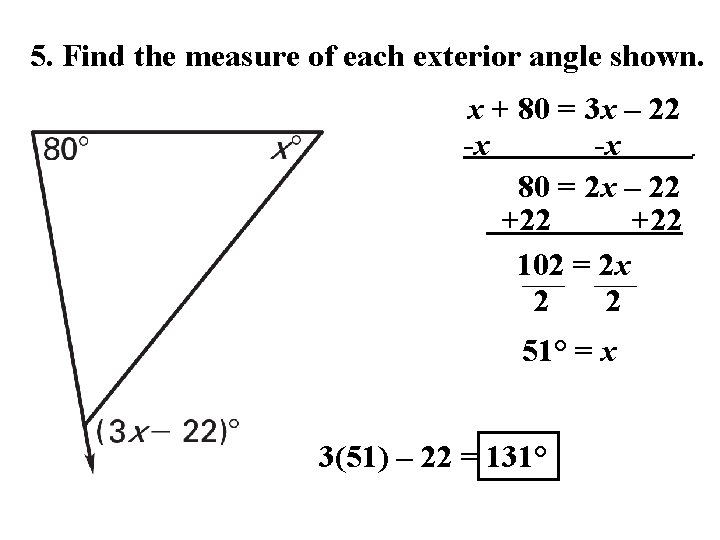
5. Find the measure of each exterior angle shown. x + 80 = 3 x – 22 -x -x 80 = 2 x – 22 +22 102 = 2 x 2 2 51° = x 3(51) – 22 = 131° .

5. Find the measure of each exterior angle shown. 2 x + 103 – x = 6 x – 7 x + 103 = 6 x – 7 -x -x 103 = 5 x – 7 +7 +7 110 = 5 x 5 5 22° = x 6(22) – 7 = 125° .

5. Find the measure of each exterior angle shown. 2 x + 3 + 51 = 4 x + 8 2 x + 54 = 4 x + 8 -2 x 54 = 2 x + 8 46 = 2 x 23° = x 4(23) + 8 = 100° .

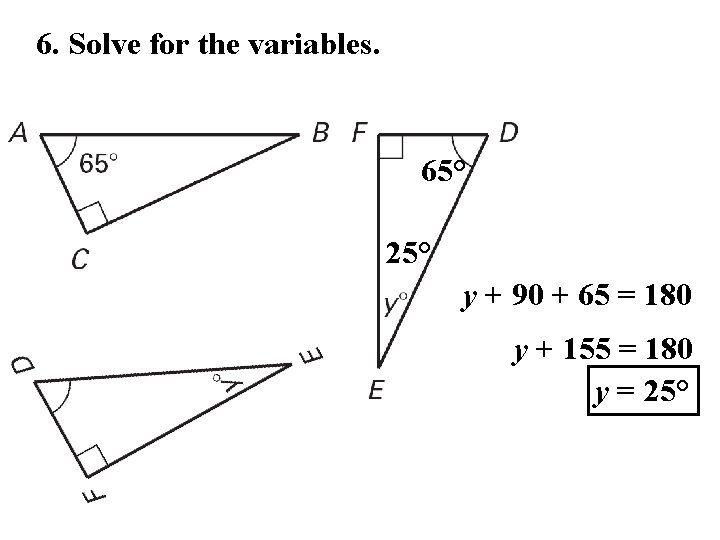
6. Solve for the variables. 65° 25° y + 90 + 65 = 180 y + 155 = 180 y = 25°

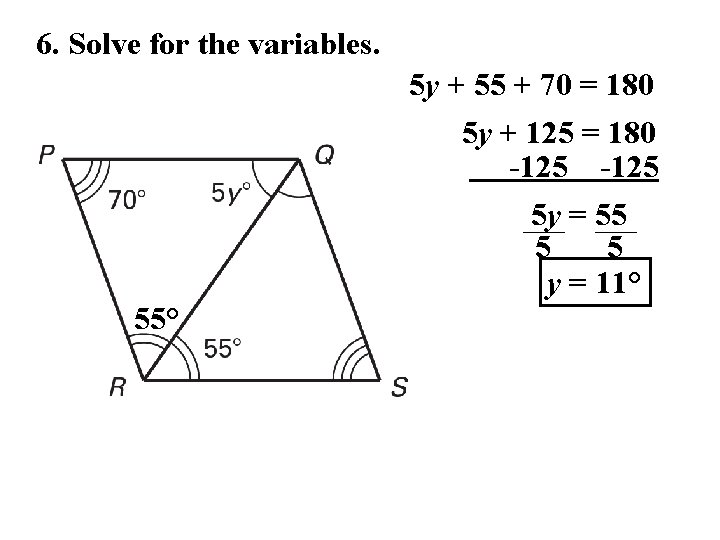
6. Solve for the variables. 5 y + 55 + 70 = 180 5 y + 125 = 180 -125 5 y = 55 5 5 y = 11° 55°

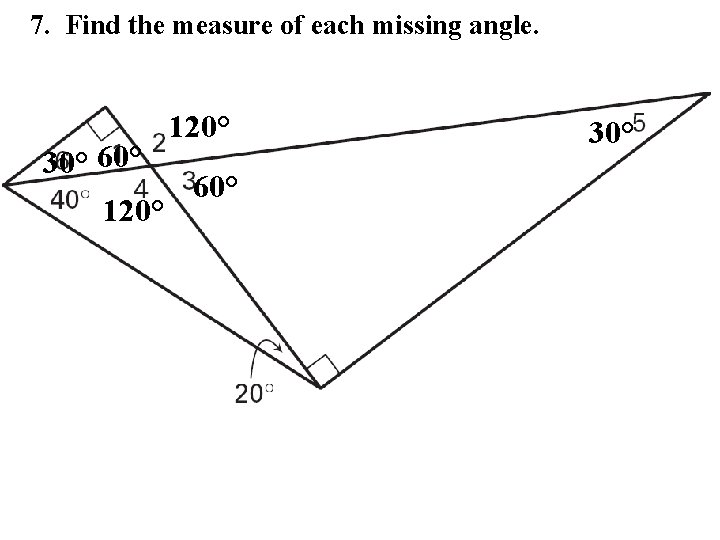
7. Find the measure of each missing angle. 120° 30° 60° 120° 30°

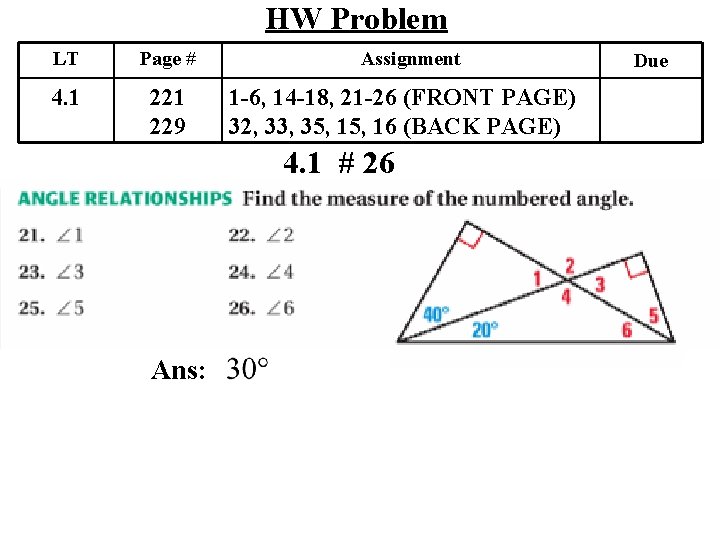
HW Problem LT Page # 4. 1 229 Assignment 1 -6, 14 -18, 21 -26 (FRONT PAGE) 32, 33, 35, 16 (BACK PAGE) 4. 1 # 26 Ans: Due